Problème de montant

Dans la fameuse tâche avec les pièces, qui doivent compter le changement, comme vous le savez, il y a deux problèmes .
- le premier est le nombre de coupures de pièces,
- le second est le nombre de chiffres représentant le changement.
Et ces deux quantités ont un effet exponentiel sur la charge de la machine de Turing, qui est en fait impliquée dans le calcul.
Reconnaître qu'une personne a deux dépendances à la fois n'est pas accepté même dans la société des alcooliques. Par conséquent, j'ai décidé de jouer prudemment et de me débarrasser d'un de ces problèmes à l'avance. La façon dont ce sera le nombre de coupures de pièces.

En résumé, l' essence du problème est décrite comme suit: la dépendance exponentielle. C'est-à-dire que la libération d'un nouveau type de pièces d'une valeur inexistante entraîne une double augmentation du nombre de combinaisons de pièces. Une autre dénomination - deux fois plus, et ainsi de suite à l'infini conditionnel. Avec une inflation galopante, lorsque de nouvelles pièces / billets sont émis assez souvent, vous devrez acheter un ordinateur plus puissant pour résoudre le problème. Et où trouver l'argent pour une inflation galopante?

Donc, une solution qui est en fait assez simple.
Si vous imaginez un segment de zéro à C (changement) avec les points correspondant aux dénominations de pièces, alors toute personne intelligente verra approximativement l'image suivante:

Eh bien, peut-être de différentes couleurs.
Alors, que pouvons-nous dire des points rouges? Bien sûr, le fait que le nombre correspondant à l'un de ces points est le montant que nous pouvons donner sous forme de changement. Et avec une pièce. Peut-être que quelqu'un a vu autre chose, mais moi, en tant qu'artiste, j'ai investi précisément ce sens. Et, en tant qu'artiste, je vais dessiner un autre point dans cette image qui correspond à la somme du premier point (de gauche à droite) avec le même point (d'accord: vous obtenez une valeur double face). Je dessine dans la même couleur, car un nouveau point signifie la même chose - ce montant peut également être un changement.

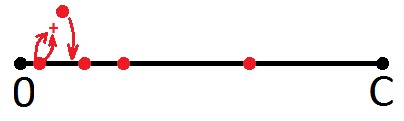
Ensuite, je prends le premier point et résume avec le second, même si le deuxième point est le montant précédent (cela n'a pas d'importance, car tous les points sont égaux ici). Je vais à nouveau mettre un nouveau point sur le segment.

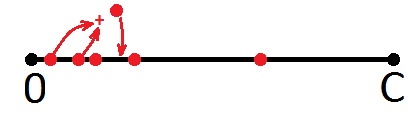
Si le nouveau point dépasse les limites du segment, nous ne dessinons rien, mais retournons au début du segment et prenons le point suivant, c'est-à-dire le second. Plus loin la même (de gauche à droite).
En fait, lorsque le point C (je vous le rappelle, c'est le changement) devient rouge, nous pouvons supposer qu'une solution a été trouvée. Et vous pouvez parcourir le cycle complet et trouver la solution optimale, de sorte que le nombre de pièces soit minimal.

Du point de vue de la programmation, il y a deux cycles. Le premier est de 0 à C / 2 (il n'est pas nécessaire de prendre le premier point d'un C / 2 plus grand, car le deuxième point est toujours plus grand que le premier et au total, il dépassera les limites du segment). Le deuxième cycle est intégré dans le premier, il part du même point que le cycle externe pointe vers et jusqu'à ce que la somme quitte les limites du segment.
En fait, c'est un buste: nous ne perdons pas une seule option, et nous sommes assurés de trouver la solution optimale, ou nous conclurons qu'il n'y a pas de solution.

Comptons la quantité d'itération à l' intérieur de nos boucles. Dans le cycle externe c'est C / 2, dans le cycle interne c'est à peu près la même chose. Multipliez C / 2 * C / 2 = (C ^ 2) / 4. Arrondissez à C au carré. Il s'agit de la pire option lorsque l'ensemble de notre segment se compose simplement de points rouges. S'il y a des espaces entre les points, le nombre d'itérations diminuera considérablement.
Comme vous pouvez le voir, pour déterminer la difficulté de résoudre le problème, nous n'utilisons pas le nombre de coupures. Cette valeur n'affecte pas directement la complexité de la solution. Les valeurs de ces dénominations affectent, disons, une pièce de 1 cent et rendent ce segment complètement rouge. Par conséquent, il vaut mieux ne pas tenir compte de cette pièce, et à la fin de la décision, prendre le point rouge le plus proche de C et dessiner au-dessus d'un cent. Mais c'est déjà le moment d'optimisation de l'algorithme, et cela dépasse le cadre de cet article.

C'est en fait tout ce que je voudrais dire. Une version de travail du programme peut être trouvée ici: lien github

1. Dans le fichier init.h, définissez COINS_NUMBER - le nombre de coupures de pièces et AMOUNT - le montant de la modification.
2. Dans le fichier coinc.c, spécifiez les dénominations des pièces dans le tableau des pièces.
3. Sous Linux, exécutez make_sh.
4. Exécutez le programme d'application pour l'exécution


Permettez-moi de vous donner un exemple amusant. Imaginez que dans certains pays les mathématiciens sont arrivés au pouvoir et ont mis en circulation 32 coupures: 2, 3, 5, 7, 11, 13, 17, 19 ... 131. Pour la commodité du comptage, seuls les nombres premiers ont été choisis (enfin, c'est pas drôle ?). Et afin de s'assurer que la réforme monétaire a réussi, ils ont envoyé un messager dans le magasin du messager pour échanger une facture 5333 (également un nombre premier). Le caissier d'une ancienne solution monocœur a résolu le problème: 39 pièces d'une valeur nominale de 131 Pythagore, une pièce 127 et une 97. Le calcul a pris 3 secondes et un peu plus d'un mégaoctet de mémoire. Le gouvernement a été informé que la population est satisfaite de la réforme, croit-il rapidement.


Et un exemple un peu plus difficile à vérifier. Pièces de monnaie, cent coupures dans une séquence aussi étrange: 0101, 0202, 0303 ... 9898, 9999, 100100. Quantité de changement: 101010. La recherche d'une solution a pris 1 seconde et un peu plus d'un mégaoctet de mémoire. Mais la décision, en fait, n'est pas, c'est-à-dire qu'il est impossible de collecter un tel montant avec de telles pièces. Avec les mêmes pièces, un chèque de 1 million prendra 26 mégaoctets et des centaines de secondes, ce qui indique une dépendance exponentielle du montant, mais pas du nombre de coupures.