👷 📛 🛸 Cosmologie et fluctuations quantiques dans le navigateur 🏆 👨🏽‍🚀 😝

Fixons-nous un objectif purement pratique: mettre en œuvre un canevas sans fin avec la possibilité de le déplacer et de le mettre à l'échelle avec la souris. Un tel canevas, par exemple, peut servir de système de coordonnées en mouvement dans un éditeur graphique. La mise en œuvre de notre idée n'est pas si compliquée, mais le processus de compréhension est associé à des objets mathématiques et physiques fondamentaux, que nous considérerons au fur et à mesure de notre développement.

Résultat

Énoncé du problème

À partir de notre toile, nous voulons effectuer seulement deux fonctions: déplacer la souris et le mouvement de la souris, ainsi que zoomer lors du défilement. L'arène de nos transformations choisira un navigateur. Les armes, dans ce cas, n'ont pas à choisir.

Machine d'état

Le comportement de ces systèmes est commodément décrit par des transitions entre leurs états, c'est-à-dire machine d'état $\ delta: S \ rightarrow S$ où $\ delta$ - la fonction de transition entre états, affichant de nombreux états en soi.

Dans notre cas, le diagramme d'état ressemble à ceci:

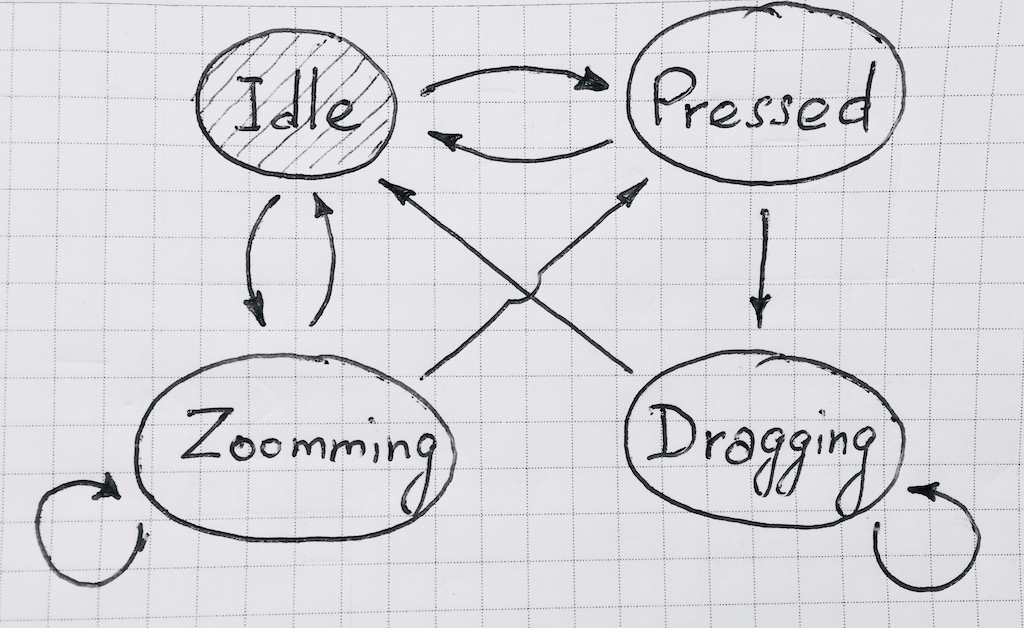
Lors de la mise en œuvre de la fonction de transition, il est pratique de rendre l'événement dépendant. Cela deviendra apparent à l'avenir. De même, il est pratique de pouvoir souscrire à un changement d'état de la machine.

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; };

Nous allons reporter l'implémentation pendant un certain temps et reprendre les transformations géométriques qui sous-tendent notre tâche.

Géométries

Si le problème du déplacement de la toile est si évident que nous ne nous attarderons pas dessus, l'étirement doit être considéré plus en détail. Tout d'abord, nous exigeons que l'étirement laisse un seul point fixe - le curseur de la souris. La condition de réversibilité doit également être satisfaite, c'est-à-dire la séquence inverse des actions de l'utilisateur doit ramener le canevas à sa position d'origine. Quelle géométrie convient à cela? Nous considérerons un groupe de transformations ponctuelles du plan en lui-même $\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$ , qui s'exprime généralement par l'introduction de nouvelles variables $x ', y'$ définis comme des fonctions de l'ancien:

x^{'} = v a r p h i (x, y) y^{'} = p s i (x, y)

$x '= \ varphi (x, y) \\ y' = \ psi (x, y)$

Conformément au principe de dualité en mathématiques, de telles transformations peuvent être interprétées comme un changement dans le système de coordonnées, ainsi qu'une transformation de l'espace lui-même avec ce dernier fixé. La deuxième interprétation convient à nos besoins.

Une compréhension moderne de la géométrie est différente d'une compréhension des anciens. Selon F. Klein , - la géométrie étudie les invariants par rapport à certains groupes de transformation. Donc, dans un groupe de mouvements $D$ l'invariant est la distance entre deux points $d ((x_ {1}, y_ {1}), ((x_ {2}, y_ {2})) = \ sqrt {(x_ {1} - x_ {2}) ^ 2+ (y_ {1 } - y_ {2}) ^ 2}$ . Il comprend la césure parallèle $T _ {(x, y)}$ sur le vecteur $(x, y)$ rotation $R _ {\ phi}$ par rapport à l'origine à un angle $\ phi$ et reflets $M_ {l}$ par rapport à une ligne $l$ . Ces mouvements sont appelés élémentaires. La composition des deux mouvements appartient à notre groupe et se résume parfois à l'élémentaire. Ainsi, par exemple, deux réflexions miroir consécutives par rapport aux lignes droites $l$ et $n$ donner une rotation autour d'un certain centre sous un certain angle (vérifiez par vous-même):

M_{l} c i r c M_{n} = T_{(- a, - b)} c i r c R_{a l p h a} c i r c T_{(a, b)}

$M_ {l} \ circ M_ {n} = T _ {(- a, -b)} \ circ R _ {\ alpha} \ circ T _ {(a, b)}$

Vous avez sûrement déjà deviné qu'un tel groupe de mouvements $D$ forme la géométrie euclidienne. Cependant, l'étirement ne préserve pas la distance entre deux points, mais leur relation. Par conséquent, un groupe de mouvements, bien qu'il devrait être inclus dans notre schéma, mais uniquement en tant que sous-groupe.

La géométrie qui nous convient est basée sur un groupe d'étirement $P$ auquel s'ajoute, outre les mouvements ci-dessus, l'homothétie $S_ {k}$ par coefficient $k$ .

Eh bien, le dernier. L'élément inverse doit être présent dans le groupe. Et donc il y a un neutre $e$ (ou célibataire) qui ne change rien. Par exemple

S_{k} c i r c S_{k}^{- 1} = e

$S_ {k} \ circ S_ {k} ^ {- 1} = e$

signifie d'abord étirer

k

$k$ fois puis

$inline$ .Maintenant, nous pouvons décrire l'étirement, en laissant le pointeur du curseur de la souris fixe, dans un langage théorique de groupe:

(x, y) r i g h t a r r o w (x, y) (T_{(- c l i e n t X, - c l i e n t Y)} c i r c S_{k} c i r c T_{(c l i e n t X, c l i e n t Y)})

$(x, y) \ rightarrow (x, y) (T _ {(- clientX, -clientY)} \ circ S_ {k} \ circ T _ {(clientX, clientY)})$

Remarque 1

Dans le cas général, les réarrangements d'actions ne sont pas commutatifs (vous pouvez d'abord enlever votre manteau puis votre chemise, mais pas l'inverse).

f o r a l l (x, y) i n m a t h b b R^{2} n e q 0 R i g h t a r r o w T_{(- x, - y)} c i r c S_{k} c i r c T_{(x, y)}) n e q S_{k} c i r c T_{(- x, - y)} c i r c T_{(x, y)})

$\ forall (x, y) \ in \ mathbb {R} ^ 2 \ neq 0 \ Rightarrow T _ {(- x, -y)} \ circ S_ {k} \ circ T _ {(x, y)}) \ neq S_ {k} \ circ T _ {(- x, -y)} \ circ T _ {(x, y)})$

Exprimez le mouvement $T _ {(x, y)}$ et $S_ {k}$ et leur composition en fonction d'un vecteur dans le code

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z);

Douleur 1

Il est très étrange qu'en JavaScript il n'y ait pas de surcharge d'opérateur. Il semblerait qu'avec une utilisation aussi répandue des graphiques vectoriels et raster, il est beaucoup plus pratique de travailler avec des vecteurs ou des nombres complexes sous une forme "classique". Les concepts d'action remplaceraient les opérations arithmétiques. Ainsi, par exemple, la rotation autour d'un vecteur $a$ au coin $\ phi$ serait exprimé de manière triviale:

T_{- a} c i r c R_{p h i} c i r c T_{a} L e f t r i g h t a r r o w z r i g h t a r r o w (z - a) e^{i p h i} + a

$T _ {- a} \ circ R _ {\ phi} \ circ T_ {a} \ Leftrightarrow z \ rightarrow (z-a) e ^ {i \ phi} + a$

Malheureusement, JS ne suit pas le développement de la merveilleuse idée pythagoricienne «Le monde est un nombre», contrairement, au moins, à Python.

Notez que jusqu'à présent, nous avons travaillé avec un groupe de transformations continues. Cependant, l'ordinateur ne fonctionne pas avec des quantités continues, donc, à la suite de Poincaré, nous comprendrons un groupe continu comme un groupe infini d'opérations discrètes. Maintenant que nous avons compris la géométrie, nous devons nous tourner vers la relativité du mouvement.

Cosmologie de la toile. Grille modulaire

Depuis un siècle, en tant qu'humanité, l' expansion de l'univers est connue. En observant des objets éloignés, tels que des galaxies et des quasars, nous enregistrons le déplacement du spectre électromagnétique vers des ondes plus longues, ce que l'on appelle le décalage vers le rouge cosmologique. Toute mesure relie l'observateur, l'observé et les moyens de mesure par rapport auxquels nous effectuons nos mesures. Sans instruments de mesure, il est impossible d'établir des relations invariantes dans la nature, c'est-à-dire de déterminer la géométrie de l'Univers. Cependant, la géométrie perd son sens sans observabilité. Donc, dans notre tâche, il est agréable d'avoir des repères, comme les galaxies, par rapport à la lumière desquels nous pouvons déterminer la relativité du mouvement de notre toile. Une telle structure peut être un réseau périodique, qui bifurque à chaque fois que l'espace est agrandi deux fois.

Le réseau étant périodique, il est pratique d'adopter une algèbre modulaire. Ainsi, nous agirons en groupe $P$ aussi sur le tore $T ^ 2 = S ^ 1 \ fois S ^ 1$ . Puisque l'écran du moniteur n'est pas un plan continu, mais un réseau entier $\ mathbb {Z} ^ 2$ (on néglige maintenant que c'est fini), puis l'action du groupe $P$ doit être considéré sur un tore entier $\ mathbb {Z} _ {p} ^ 2$ où $p$ - la taille du bord du carré $p \ fois p$ :

Ainsi, une fois pour toutes fixant notre tore près de l'origine, nous y effectuerons tous les calculs ultérieurs. Ensuite, propagez-le à l'aide des méthodes de bibliothèque de canevas standard. Voici à quoi ressemble un mouvement d'un pixel:

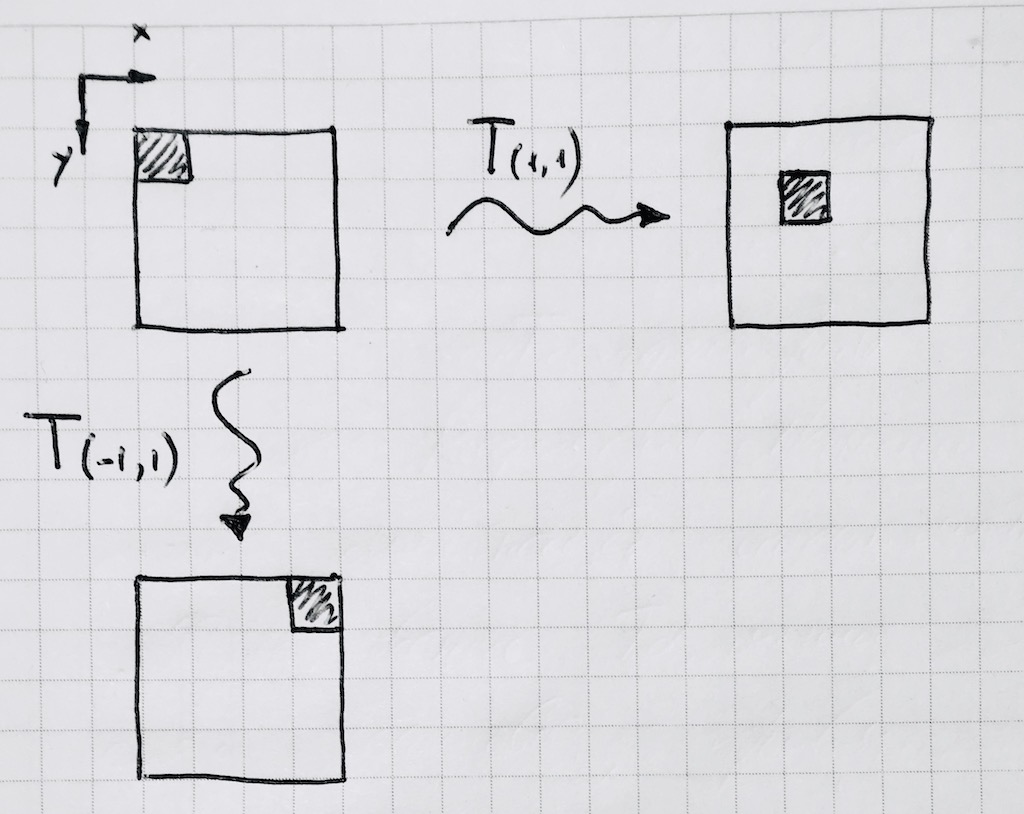
Évidemment, l'opération standard de prise du module x% p ne nous convient pas, car elle traduit des valeurs négatives de l'argument en valeurs négatives, mais sur le tore entier il n'y en a pas. Écrivez votre fonction $x \ mod p$ :

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p;

Revenons maintenant à la machine d'état finale et

le définir

La classe FSM est commodément héritée d'EventEmitter, ce qui nous permettra de nous abonner.

 class FSM<States> extends EventEmitter { static get TRANSITION() { return '__transition__'; } state: States; scheme: Scheme<States>; constructor(state: States, scheme: Scheme<States>) { super(); this.state = state; this.scheme = scheme; this.on(FSM.TRANSITION, event => this.emit(this.state, event)); } get isActive(): boolean { return typeof(this.scheme[this.state]) === 'object'; } dispatch(event: Event) { if (this.isActive) { const transition = this.scheme[this.state].find(({ where }) => where(event).every(domen => domen) ); if (transition) { this.state = transition.to; this.emit(FSM.TRANSITION, event); } } } }

Ensuite, définissez un schéma de transition, créez un canevas et

tout initialiser.

 canvas = document.getElementById('canvas'); ctx = canvas.getContext('2d'); // Create a pattern, offscreen patternCanvas = document.createElement('canvas'); patternContext = patternCanvas.getContext('2d'); type States = | 'idle' | 'pressed' | 'dragging' | 'zooming'; const scheme: Scheme<States> = { 'idle': [ { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'zooming', where: event => [event.type === 'wheel'] }, ], 'pressed': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'moving': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'zooming': [ { to: 'zooming', where: event => [event.type === 'wheel'] }, { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'idle', where: event => [true] }, ], }; const fsm: FSM<States> = new FSM('idle', scheme); const dispatch = fsm.dispatch.bind(fsm);

Ensuite, vous devez déterminer la fonction de rendu, définir les valeurs initiales nécessaires et vous abonner au changement d'état. Considérez la partie la plus intéressante du code:

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); });

Premièrement, nous ne développons pas le coefficient k, mais un certain rapport nk / k. Cela est dû au fait que l'étape m de notre cartographie à un point fixe $(a, b)$ exprimé en

x_{m} = (x_{m - 1} - a) k_{m - 1}^{*} + a y_{m} = (y_{m - 1} - b) k_{m - 1}^{*} + b

$x_ {m} = (x_ {m-1} -a) k_ {m-1} ^ * + a \\ y_ {m} = (y_ {m-1} -b) k_ {m-1} ^ * + b$

ou, par rapport aux valeurs initiales $x_ {1}, y_ {1}$

x_{m} = (x_{1} - a) p r o d_{i = 1}^{m - 1} k_{i}^{*} + a y_{m} = (y_{1} - b) p r o d_{i = 1}^{m - 1} k_{i}^{*} + b

$x_ {m} = (x_ {1} -a) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + a \\ y_ {m} = (y_ {1} -b) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + b$

Evidemment le produit $\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$ il y a une fonction non linéaire de l'étape d'itération et converge très rapidement vers zéro, ou s'enfuit à l'infini avec de petits écarts initiaux.

Nous introduisons la variable g, qui est une mesure de doublement de notre toile. Évidemment, il prend une valeur constante sur un certain intervalle. Pour atteindre la linéarité $k_ {i} ^ *$ nous utilisons une substitution homogène

k_{i + 1}^{*} = f r a c k_{i + 1} k_{i}, k_{1} = 1

$k_ {i + 1} ^ * = \ frac {k_ {i + 1}} {k_ {i}}, k_ {1} = 1$

Ensuite, tous les membres de l'œuvre, à l'exception du premier et du dernier, seront réduits:

p r o d_{i = 1}^{m - 1} k_{i}^{*} = p r o d_{i = 1}^{m - 1} f r a c k_{i} k_{i - 1} = f r a c k_{2} 1 f r a c k_{3} k_{2} . . . f r a c k_{m - 2} k_{m - 3} f r a c k_{m - 1} k_{m - 2} = k_{m - 1}

$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ * = \ prod_ {i = 1} ^ {m-1} \ frac {k_ {i}} {k_ {i-1}} = \ frac {k_ {2}} {1} \ frac {k_ {3}} {k_ {2}} ... \ frac {k_ {m-2}} {k_ {m-3}} \ frac { k_ {m-1}} {k_ {m-2}} = k_ {m-1}$

De plus, le saut de phase g réduit le taux d'expansion de telle manière que la structure fractale qui se déplie devant nous se déplace toujours de façon linéaire. Ainsi, nous obtenons une variation approximative de la loi de puissance de Hubble de l'expansion de l'Univers.

Reste à comprendre les limites de précision de notre modèle.

Fluctuations quantiques. Champ de numéro 2-adic

La compréhension du processus de mesure a conduit au concept d'un nombre réel. Le principe d'incertitude de Heisenberg pointe ses limites. Un ordinateur moderne ne fonctionne pas avec des nombres réels, mais avec des mots machine, dont la longueur est déterminée par la capacité du processeur. Les mots machine forment un champ de nombres 2-adiques $\ mathbb {Q_ {2}}$ et sont désignés comme $\ mathbb {F_ {2} ^ {n}}$ où $n$ - longueur du mot. Dans ce cas, le processus de mesure est remplacé par le processus de calcul et est associé à une métrique non archimédienne:

f o r a l l n i n m a t h b b Z, z i n m a t h b b F_{2}^{n} : n c d o t z < 2^{n}

$\ forall n \ in \ mathbb {Z}, z \ in \ mathbb {F_ {2} ^ {n}}: n \ cdot z <2 ^ n$

Ainsi, notre modèle a une limite de calcul. Les limitations sont décrites dans la norme IEEE_754 . À partir d'un moment donné, notre taille de base dépassera la limite de précision et l'opération de prise du module commencera à générer des erreurs ressemblant à des séquences pseudo-aléatoires. Ceci est simplement vérifié en supprimant la ligne

 if (g < min || g > max) return;

La limite finale dans notre cas est calculée par la méthode semi-empirique, puisque nous travaillons avec plusieurs paramètres.

Conclusion

Ainsi, apparemment distantes à première vue, les théories sont connectées sur la toile du navigateur. Les concepts d'action, de mesure et de calcul sont étroitement liés les uns aux autres. Le problème de leur combinaison n'est toujours pas résolu.