Deux pages ont suffi pour prouver l'hypothèse de 30 ans dans le domaine de l'informatique.

L'hypothèse de la «sensibilité» a dérouté de nombreux éminents informaticiens, mais ses nouvelles preuves se sont avérées si simples qu'un chercheur pourrait la réduire à un seul tweet

Les travaux publiés cet été mettent un terme à près de 30 ans d'histoire de l'hypothèse concernant la structure des éléments constitutifs fondamentaux des circuits informatiques. Cette hypothèse de «sensibilité» a laissé perplexe de nombreux éminents informaticiens pendant des années, mais ses nouvelles preuves se sont avérées si simples qu'un chercheur pourrait la réduire à un seul tweet.

"Cette hypothèse était l'un des problèmes ouverts les plus ennuyeux et honteux de toute la combinatoire et l'informatique théorique", a écrit Scott Aaronson de l'Université du Texas à Austin dans son blog. "La liste des personnes qui ont essayé de le prouver et qui ne l'ont pas fait est une liste des personnes les plus éminentes en mathématiques discrètes et en informatique théorique", a-t-il ajouté dans un e-mail.

Cette hypothèse est associée aux fonctions booléennes - les règles de conversion des chaînes de bits entrants (zéros et uns) en un seul bit. Une de ces règles produit 1 lorsque tous les bits entrants sont à 1 et 0 sinon; une autre règle renvoie 0 si la ligne contient un nombre pair d'unités et 1 dans un autre cas. Chaque circuit informatique est une combinaison de fonctions booléennes, ce qui en fait «le matériau de construction de tout ce qui se fait en informatique», a déclaré Rocco Cenedio de l'Université Columbia.


Au fil des ans, de nombreux moyens ont été développés en informatique pour mesurer la complexité d'une fonction booléenne donnée. Chaque mesure utilise son propre aspect de la façon dont les informations de ligne d'entrée déterminent le bit de sortie. Par exemple, la «sensibilité» d'une fonction booléenne, grosso modo, indique la probabilité que la modification d'un seul bit à l'entrée modifie le bit à la sortie. Et la «complexité de la demande» calcule combien de bits entrants doivent être demandés afin de savoir avec certitude ce que sera le sortant.

Chaque mesure donne son point de vue unique sur la structure d'une fonction booléenne. Cependant, les informaticiens ont constaté que presque toutes ces mesures s'inscrivent dans une plate-forme universelle, et que d'après la valeur de l'une d'entre elles, on peut approximativement juger de l'importance des autres. Et une seule mesure de la complexité ne rentre pas dans ce schéma: la sensibilité.

En 1992, Noam Nisan de l'Université hébraïque de Jérusalem et Mario Szeged, qui travaille maintenant à l'Université Rutgers, ont suggéré que la sensibilité s'inscrit toujours dans cette plateforme. Mais personne ne pouvait le prouver. "Cette question, je dirais, était en suspens dans le domaine de l'étude des fonctions booléennes", a déclaré Cenedio.

«Les gens ont écrit des travaux longs et complexes, essayant de faire très peu de progrès», a déclaré Ryan O'Donnell de l'Université Carnegie Mellon.

Et maintenant, Hao Huang , un mathématicien de l'Université Emory, a prouvé l'hypothèse de sensibilité à l'aide d'une preuve brillante mais élémentaire de deux pages liée à la combinatoire des points sur les cubes. "C'est beau, comme une perle précieuse", a écrit Claire Matthew, du Centre national de la recherche scientifique dans une interview sur Skype.

Aaronson et O'Donnell ont qualifié le travail de Juan de «preuve» de l'hypothèse de sensibilité, se référant au concept du «livre céleste» de Pal Erdös, dans lequel Dieu écrit les preuves idéales de chaque théorème. «Il m'est difficile d'imaginer que même Dieu connaît une preuve plus simple du théorème de sensibilité», a écrit Aaronson.

Sujet sensible

Imaginez, a déclaré Matthew, que vous remplissez un formulaire avec des questions sur le formulaire de demande de prêt bancaire, dont les réponses peuvent être oui / non. Lorsque vous avez terminé, le banquier évaluera les résultats et vous dira si vous êtes apte à un prêt. Ce processus est une fonction booléenne: vos réponses sont des bits entrants et la décision du banquier est sortante.

Si votre demande est refusée, vous pouvez vous demander si vous pouvez modifier le résultat en mentant dans une seule question - peut-être en déclarant que vous gagnez plus de 50 000 $ par an, bien que ce ne soit pas le cas. Si ce mensonge change le résultat de la réflexion, les informaticiens appellent une telle fonction booléenne «sensible» à la valeur d'un bit particulier. Si, par exemple, vous pourriez mentir à l'un des sept endroits et changer à chaque fois le résultat, la sensibilité de la fonction booléenne d'évaluation de votre demande de prêt est de sept.

Les informaticiens définissent la sensibilité globale d'une fonction booléenne comme la valeur de sensibilité la plus élevée pour toutes les options possibles pour remplir une application. Dans un sens, cette mesure calcule le nombre de problèmes qui seront vraiment importants dans la plupart des cas limites - dans les applications, dont le résultat est plus facilement modifié si les applications elles-mêmes sont légèrement modifiées.


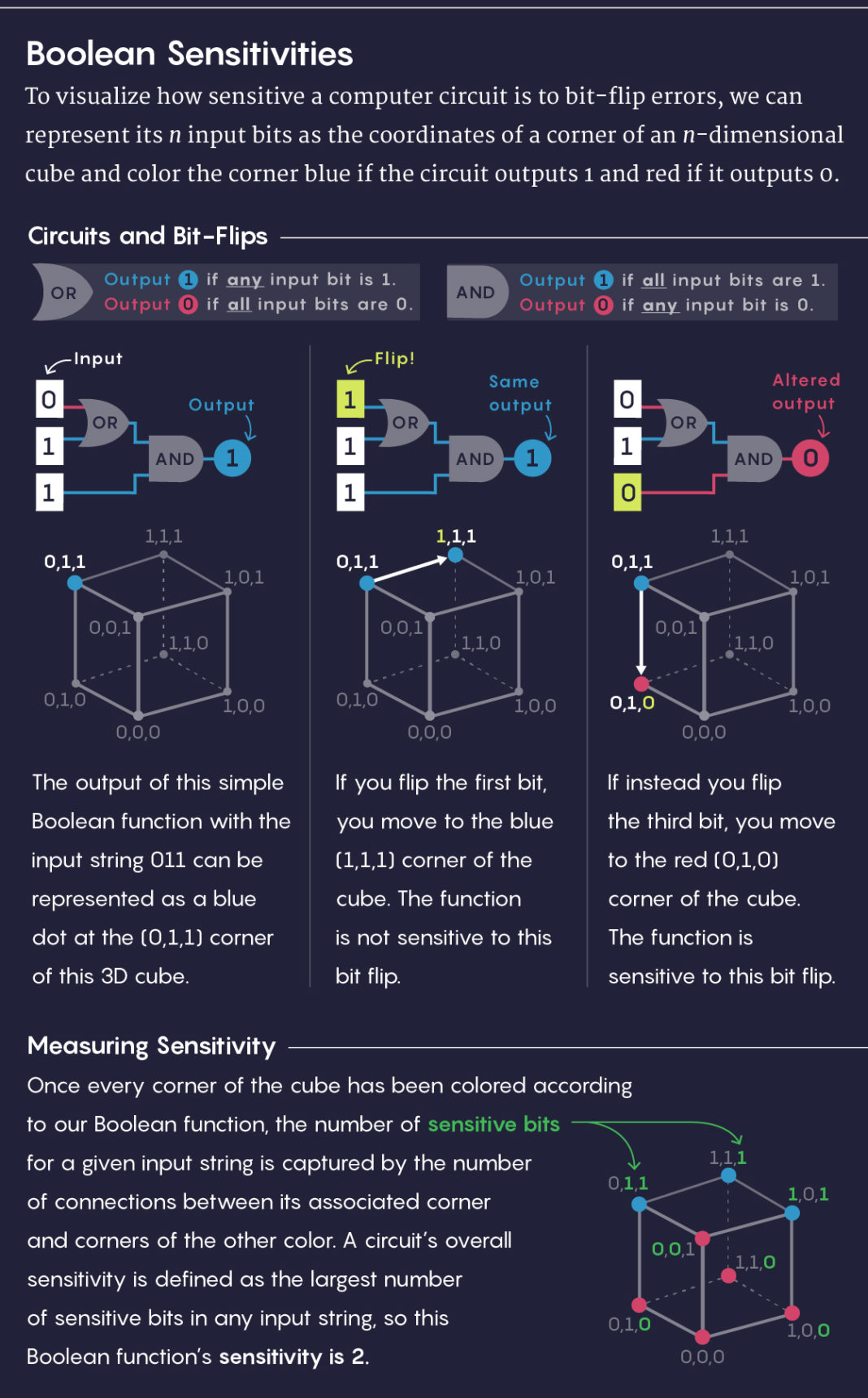Pour visualiser la sensibilité du circuit aux erreurs avec l'inversion des bits, n bits entrants peuvent être représentés comme les coordonnées des sommets d'un cube à n dimensions. Nous colorerons le sommet en bleu si le chemin produit 1 et en rouge si 0.

Au milieu à gauche: la sortie d'une simple fonction booléenne avec l'entrée 011 peut être représentée par un point bleu en haut du cube (0,1,1).
Centre: en tournant le premier bit, nous irons au sommet bleu du cube (1,1,1). La fonction n'est pas sensible à l'inversion de ce bit.
Au milieu à droite: en tournant le troisième bit, nous irons au sommet rouge du cube (0,1,0). La fonction est sensible à l'inversion de ce bit.

Après avoir coloré tous les sommets du cube, nous obtenons le nombre de bits sensibles pour une ligne entrante donnée égal au nombre de connexions entre le sommet correspondant et les sommets d'une couleur différente. La sensibilité de boucle est définie comme le plus grand nombre de bits sensibles dans une ligne d'entrée, donc cette fonction a une sensibilité de 2.

La sensibilité est généralement l'une des mesures les plus simples pour calculer la complexité, mais ce n'est pas du tout une mesure explicative simple. Par exemple, notre banquier, au lieu de vous donner un formulaire à remplir, pourrait commencer par une seule question, puis utiliser votre réponse pour déterminer la question à poser ensuite. Le plus grand nombre de questions qu'un banquier devra poser avant de prendre une décision est la complexité de la demande d'une fonction booléenne.

Une telle mesure apparaît dans diverses situations - par exemple, un médecin peut vouloir envoyer le patient pour recueillir le moins de tests possible afin de poser un diagnostic, ou un expert en apprentissage automatique peut vouloir créer un algorithme qui étudie le moins de propriétés de l'objet possible avant il pourra le classer correctement. "Dans de nombreuses situations - diagnostic ou formation - vous aimez que la règle de base ait une faible complexité de requête", a déclaré O'Donnell.

Entre autres mesures, il y a la recherche du moyen le plus simple d'écrire une fonction booléenne sous la forme d'une expression mathématique, ou de calculer le nombre de réponses que le banquier devra montrer au patron afin de prouver que la demande a été traitée correctement. Il existe même une variante de la complexité de la requête de la physique quantique, lorsque le banquier pose une «superposition» de plusieurs questions à la fois. Comprenant comment cette mesure est liée à d'autres mesures de complexité, les chercheurs comprennent mieux les limites des algorithmes quantiques.

Les informaticiens ont prouvé qu'il existe une relation étroite entre toutes ces mesures, à l'exception de la sensibilité. Plus précisément, ils ont constaté qu'ils sont liés les uns aux autres par la dépendance polynomiale - par exemple, une mesure peut être exprimée comme un carré ou un cube d'une autre. Et seule la sensibilité a obstinément résisté, ne voulant pas s'intégrer dans ce schéma de classification pratique. De nombreux chercheurs soupçonnaient qu'il devrait lui convenir, mais n'ont pas pu prouver qu'il n'y a pas de fonctions booléennes étranges dont la sensibilité est liée à d'autres mesures non pas par polynôme mais par dépendance exponentielle, ce qui dans ce cas signifierait que la mesure de sensibilité est fondamentalement plus petit que le reste.

"Cette question a gardé les gens éveillés pendant 30 ans", a déclaré Aaronson.

Accrochez la solution

Juan a découvert cette hypothèse fin 2012, lors d'un dîner avec le mathématicien Michael Sachs de l'Institute for Advanced Studies, où Juan était post-doctorant. Il fut immédiatement fasciné par la simplicité et l'élégance de l'hypothèse. "Et à partir de ce moment, je suis devenu obsédé par ses pensées", a-t-il déclaré.

Juan a ajouté l'hypothèse de sensibilité à la «liste secrète» des problèmes qui l'intéressaient et lorsqu'il a découvert un nouvel outil mathématique, il s'est demandé s'il pouvait l'aider. «Chaque fois après la publication d'un autre ouvrage, je suis retourné à cette tâche», a-t-il déclaré. «Bien sûr, j'ai alloué du temps et de l'énergie pour travailler sur des tâches plus réalistes.»


Hao Huang en vacances récentes à Lisbonne

Juan, comme beaucoup dans la communauté des chercheurs, savait que l'hypothèse de sensibilité peut être prouvée si les mathématiciens peuvent prouver une autre hypothèse avec une condition plus simple concernant un ensemble de points sur des cubes de différentes dimensions. Il existe un moyen naturel de passer d'une chaîne de zéros et de uns à un point sur un cube à n dimensions: il suffit d'utiliser n bits comme coordonnées de ce point.

Par exemple, quatre lignes à deux bits - 00, 01, 10 et 11 - correspondent aux quatre coins d'un carré sur un plan à deux dimensions: (0,0), (0,1), (1,0) et (1,1). De même, huit chaînes de trois bits correspondent à huit coins d'un cube en trois dimensions, et ainsi de suite, pour des dimensions supérieures. La fonction booléenne peut être considérée comme la règle de coloration de ces angles de cube avec deux couleurs différentes (par exemple, rouge pour 0 et bleu pour 1).

En 1992, Craig Gotsman , qui travaille maintenant au New Jersey Institute of Technology et à Nati Lignal de l'Université hébraïque, s'est rendu compte que la preuve de l'hypothèse de sensibilité peut être réduite à la réponse à une simple question sur les cubes de différentes dimensions: si vous prenez un ensemble composé de plus de la moitié des sommets des cubes , et les colorier en rouge, est-il nécessaire de trouver un point rouge connecté à de nombreux autres points rouges (par points "connectés" nous voulons dire que deux sommets sont reliés par un bord commun, et non situés en diagonale).

Si notre sous-ensemble contient exactement la moitié des sommets du cube, ils peuvent ne pas être connectés les uns aux autres. Par exemple, parmi les huit coins d'un cube en trois dimensions, il y a quatre points,
(0,0,0), (1,1,0), (1,0,1) et (0,1,1) sont situés en diagonale l'un de l'autre. Mais dès que plus de la moitié des sommets d'un cube de n'importe quelle dimension deviennent rouges, parmi eux les points rouges doivent être connectés entre eux. La question est de savoir comment ces connexions sont réparties? Y aura-t-il au moins un de ces pics avec plus de connexions?

En 2013, Juan a commencé à penser que la meilleure façon de comprendre ce problème serait probablement d'utiliser la méthode standard de représentation du réseau à l'aide d'une matrice qui garde la trace des points connectés et étudie ensuite de nombreux nombres appelés valeurs propres de la matrice. Pendant cinq ans, il revient périodiquement sur cette idée, mais en vain. "Au moins à cause de ce que je pensais d'elle avant d'aller au lit, il était plus facile pour moi de dormir pendant de nombreuses nuits", a-t-il commenté sur le blog d'Aaronson.

Puis en 2018, Juan a pensé à utiliser le théorème d'alternance de Cauchy, un énoncé mathématique d'il y a 200 ans, reliant les valeurs propres d'une matrice à une sous-matrice, ce qui en fait peut-être un outil idéal pour étudier la relation entre un cube et un sous-ensemble de ses sommets. Juan a décidé de demander une subvention à la State Science Foundation pour approfondir cette idée.

Puis, le mois dernier, assis dans un hôtel à Madrid et remplissant une demande de subvention, il s'est soudain rendu compte qu'il pouvait étendre l'utilisation de cette approche jusqu'à la fin, en changeant simplement les signes de certains chiffres de la matrice. De cette façon, il a pu prouver que dans tout ensemble de plus de la moitié des sommets d'un cube à n dimensions, il existera un point associé à au moins √n autres points - et l'hypothèse de sensibilité découle immédiatement de ce résultat.

Lorsque Matthew a reçu le travail de Juan par courrier, sa première réaction a été "oups", a-t-elle déclaré. «Lorsqu'une tâche existe depuis 30 ans et que tout le monde la connaît, sa preuve doit être soit très longue et complexe, soit très profonde.» Elle a ouvert le dossier avec l'œuvre, s'attendant à ne rien comprendre.

Cependant, la preuve était assez simple pour que Matthew et d'autres chercheurs puissent la digérer en une seule séance. «Je pense que cet automne, les étudiants lui parleront dans le cadre d'une conférence de chaque cours de maîtrise en combinatoire», a-t-elle écrit sur Skype.

Le résultat de Juan s’est avéré encore plus fort que nécessaire pour prouver cette hypothèse, et cette force devrait nous donner de nouvelles idées sur les mesures de la complexité. "Il a été ajouté à notre boîte à outils et peut aider à répondre à d'autres questions liées aux fonctions booléennes", a déclaré Cenedio.

Mais surtout, le résultat de Juan nous permet de mettre fin à tous les soucis de savoir si la sensibilité est un étranger étrange dans le monde des mesures de complexité, a déclaré Cenedio. «Je pense que le soir, en apprenant ces résultats, beaucoup ont pu dormir paisiblement.»