Jouer avec des nombres complexes

Salut

Un autre essai. Jouons cette fois avec des nombres complexes, avec des formules et leur visualisation.

Idée

Un nombre complexe est une certaine extension d'un nombre réel, en fait un vecteur pour lequel un ensemble entier d'axiomes est défini. Tout nombre complexe (et donc réel) peut être écrit comme $$$z = a + bi$où a est la partie réelle, b est la partie imaginaire, i est la racine de l'équation $$$x ^ {2} = - 1$. De nombreuses opérations sont définies pour lui, qui sont définies pour un nombre réel, par exemple, $$$z_1 + z_2 = a_1 + a_2 + (b_1 + b_2) i$. 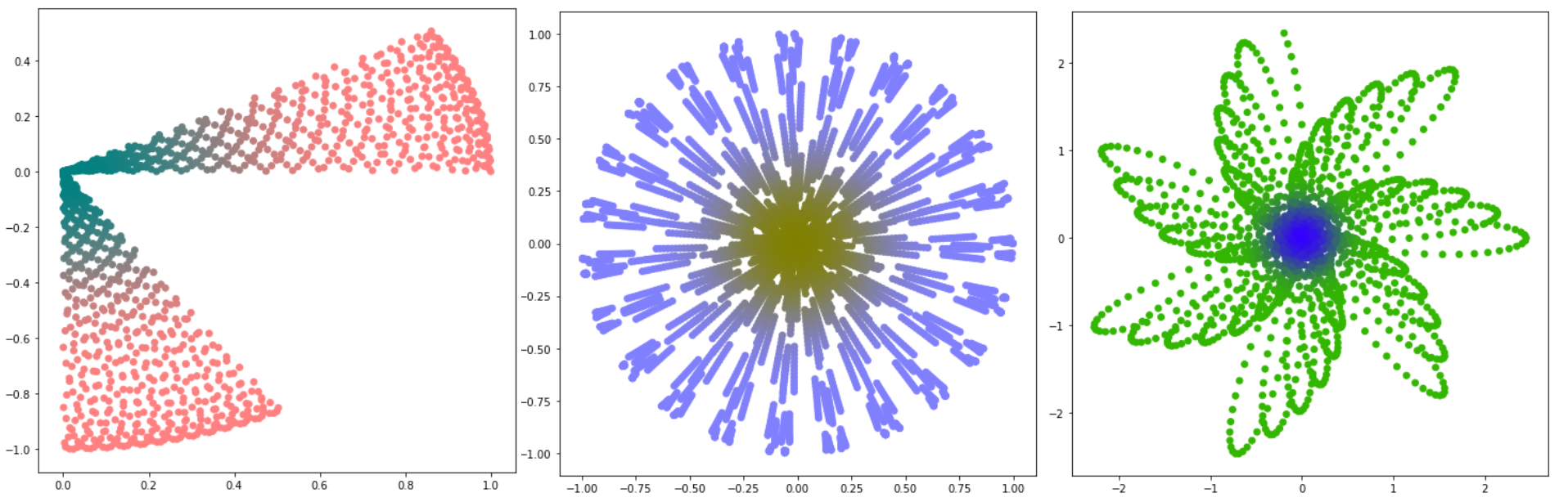Fait intéressant, si vous effectuez diverses opérations avec eux, augmentez le pouvoir, multipliez, etc., puis prenez $$$Re (z)$(partie réelle) pour l'axe Ox, et $$$Im (z)$(partie imaginaire) pour l'axe Oy, vous pouvez obtenir des images amusantes.

Au fait, j'ai moi-même trouvé toutes les formules suivantes.

Fonction de visualisation

Routine. La fonction, qui selon cette fonction itérative tire tout sur le terrain:

import random import numpy as np def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[8, 8]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show() 

Toutes nos fonctions dépendent de deux paramètres A et B. De plus, nous itérons sur B à l'intérieur de vis (), et A est le paramètre global de la fonction.

La fonction Curl

$$

$$f (A, B) = Bsin (B) * e ^ {iBcos (A)}$$

Sa déclaration en python:

 def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Et courir

 A = 121.5 vis(A, func_1, step=0.1) 

Et le résultat pour A = 121,5:



Et pour A = 221,5:



Notez que ces nombres ne découlent pas du calcul d'une intégrale définie sur une variété lisse et d'autres mots intelligents qui n'ont aucun sens dans ce contexte. Ce sont vraiment des nombres aléatoires, et il y a toujours exactement une infinité de différents A, à la suite de quoi la beauté est obtenue.

Besoin de peindre

Nous déclarons une fonction de couleur (une telle fonction qui renvoie un tuple de trois nombres en coordonnées):

 def sigm(x): #         0  1 return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5) 

Choisissez un paramètre aléatoire A, qu'il soit 149:

 vis(149, func_1, step=0.1, c=color_1) 

Fonction oies

Les oies sont décrites comme suit:

$$

$$f (A, B) = cos (B) sin (B) * B * e ^ {iBcos (A)}$$

Déclaration Python:

 def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Son résultat pour A = 106:

Fonction focaccia

$$

$$f (A, B) = cos (B (A + 1)) * e ^ {iBcos (A)}$$

 def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A))) 

 vis(246, func_3, step=0.1, c=color_2) 

 vis(246, func_3, step=0.1, c=color_2) 

Fonction sans titre

$$

$$f (A, B) = Bsin (A + B) * e ^ {iBsin (A)}$$

 color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) vis(162, func_4, step=0.1, c=color_3) 

 vis(179, func_4, step=0.1, c=color_3) 

Formule beauté

$$

$$f (A, B) = cos (B (A + 1)) ^ {\ frac {3} {2}} * e ^ {iBcos (A)}$$

 def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A))) 

 color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) vis(345, func_5, step=0.1, c=color_4) 

 vis(350, func_5, step=0.1, c=color_4) 

C'est tout pour l'instant.