Je m'appelle Vyacheslav, je suis mathématicien chronique et depuis plusieurs années je n'ai pas utilisé de cycles pour travailler avec des tableaux ...
Exactement depuis que j'ai découvert les opérations vectorielles dans NumPy. Je veux vous présenter les fonctions NumPy que j'utilise le plus souvent pour traiter des tableaux de données et d'images. À la fin de l'article, je montrerai comment vous pouvez utiliser la boîte à outils NumPy pour convoluer des images sans itérations (= très rapide).
N'oubliez pas
import numpy as np
et c'est parti!
Table des matières
Qu'est-ce que numpy?Création de tableauxAccès aux éléments, tranchesLa forme du tableau et son évolutionRéarrangement et transposition des axesArray joinClonage de donnéesOpérations mathématiques sur les éléments du tableauMultiplication matricielleAgrégateursAu lieu d'une conclusion - un exempleQu'est-ce que numpy?
Il s'agit d'une bibliothèque open source qui s'est séparée du projet SciPy. NumPy est le descendant de Numeric et NumArray. NumPy est basé sur la bibliothèque LAPAC, qui est écrite en Fortran. Matlab est une alternative non python pour NumPy.
Du fait que NumPy est basé sur Fortran, c'est une bibliothèque rapide. Et du fait qu'il prend en charge les opérations vectorielles avec des tableaux multidimensionnels, il est extrêmement pratique.
En plus de la version de base (tableaux multidimensionnels dans la version de base), NumPy comprend un ensemble de packages pour résoudre des tâches spécialisées, par exemple:
- numpy.linalg - implémente des opérations d'algèbre linéaire (une simple multiplication de vecteurs et de matrices est dans la version de base);
- numpy.random - implémente des fonctions pour travailler avec des variables aléatoires;
- numpy.fft - implémente la transformée de Fourier directe et inverse.
Je vous propose donc de ne considérer en détail que quelques fonctionnalités de NumPy et des exemples de leur utilisation, qui vous suffiront pour comprendre la puissance de cet outil!
<up>Création de tableaux
Il existe plusieurs façons de créer un tableau:
- convertir la liste en tableau:
A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]])
- copiez le tableau (copie et copie complète requises !!!):
B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]])
- créer un zéro ou un tableau d'une taille donnée:
A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]])
B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]])
Ou prenez les dimensions d'un tableau existant:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]])
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]])
- lors de la création d'un tableau carré à deux dimensions, vous pouvez en faire une matrice diagonale unitaire:
A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
- construire un tableau de nombres de De (y compris) à À (non compris) avec l'étape Step:
From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])
Par défaut, from = 0, step = 1, donc une variante avec un paramètre est interprétée comme To:
A = np.arange(5) A Out: array([0, 1, 2, 3, 4])
Ou avec deux - comme From et To:
A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14])
Notez que dans la méthode n ° 3, les dimensions du tableau ont été transmises comme
un paramètre (un tuple de tailles). Deuxième paramètre des méthodes n ° 3 et n ° 4, vous pouvez spécifier le type d'élément de tableau souhaité:
A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]])
B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]])
En utilisant la méthode astype, vous pouvez convertir le tableau en un type différent. Le type souhaité est indiqué en paramètre:
A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32')
Tous les types disponibles peuvent être trouvés dans le dictionnaire sctypes:
np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]}
<up>Accès aux éléments, tranches
L'accès aux éléments du tableau se fait par des indices entiers, le compte à rebours commence à 0:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5
Si vous imaginez un tableau multidimensionnel comme un système de tableaux unidimensionnels imbriqués (un tableau linéaire, dont les éléments peuvent être des tableaux linéaires), il devient évident que vous pouvez accéder aux sous-tableaux à l'aide d'un ensemble d'indices incomplet:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6])
Compte tenu de ce paradigme, nous pouvons réécrire l'exemple de l'accès à un élément:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5
Lorsque vous utilisez un ensemble d'indices incomplet, les indices manquants sont implicitement remplacés par une liste de tous les indices possibles le long de l'axe correspondant. Vous pouvez le faire explicitement en définissant ":". L'exemple précédent avec un index peut être réécrit comme suit:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6])
Vous pouvez ignorer un index le long d'un ou de plusieurs axes; si l'axe est suivi d'axes avec indexation, ":" doit:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5])
Les index peuvent prendre des valeurs entières négatives. Dans ce cas, le nombre est à la fin du tableau:
A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4
Vous pouvez utiliser non pas des index uniques, mais des listes d'index le long de chaque axe:
A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4])
Ou des plages d'index sous la forme "De: À: Étape". Cette conception est appelée une tranche. Tous les éléments sont sélectionnés selon la liste des index à partir de l'index From inclusivement, jusqu'à l'index To sans
inclure avec l'étape Step:
A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2])
L'étape d'index a une valeur par défaut de 1 et peut être ignorée:
A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
Les valeurs From et To ont également des valeurs par défaut: 0 et la taille du tableau le long de l'axe d'index, respectivement:
A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4])
Si vous souhaitez utiliser From et To par défaut (tous les indices sur cet axe) et que l'étape est différente de 1, vous devez utiliser deux paires de deux-points afin que l'interpréteur puisse identifier un seul paramètre comme Step. Le code suivant «étend» le tableau le long du deuxième axe, mais ne change pas le premier:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
Maintenant faisons-le
print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]]
Comme vous pouvez le voir, via B, nous avons modifié les données en A. C'est pourquoi il est important d'utiliser des copies dans les tâches réelles. L'exemple ci-dessus devrait ressembler à ceci:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
NumPy offre également la possibilité d'accéder à plusieurs éléments de tableau via un tableau d'index booléen. Le tableau d'index doit correspondre à la forme de celui indexé.
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6])
Comme vous pouvez le voir, une telle construction renvoie un tableau plat composé d'éléments du tableau indexé qui correspondent à de vrais index. Cependant, si nous utilisons un tel accès aux éléments du tableau pour changer leurs valeurs, la forme du tableau sera préservée:
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Les opérations logiques logic_and, logic_or et logic_not sont définies sur l'indexation des tableaux booléens et effectuent les opérations logiques AND, OR et NOT par élément:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]]
Logic_and et Logic_or prennent 2 opérandes, Logic_Not en prend un. Vous pouvez utiliser les opérateurs &, | et ~ pour exécuter AND, OR et NOT, respectivement, avec un nombre quelconque d'opérandes:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Ce qui équivaut à utiliser uniquement I1.
Il est possible d'obtenir un tableau logique d'indexation correspondant sous forme à un tableau de valeurs en écrivant une condition logique avec le nom du tableau comme opérande. La valeur booléenne de l'index sera calculée comme la vérité de l'expression pour l'élément de tableau correspondant.
Recherchez un tableau d'indexation d'éléments I supérieurs à 3 et les éléments dont les valeurs sont inférieures à 2 et supérieures à 4 seront réinitialisés à zéro:
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]]
<up>La forme du tableau et son évolution
Un tableau multidimensionnel peut être représenté comme un tableau unidimensionnel de longueur maximale, coupé en fragments le long du dernier axe et posé en couches le long des axes, en commençant par ce dernier.
Pour plus de clarté, considérons un exemple:
A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]]
Dans cet exemple, nous avons formé 2 nouveaux tableaux à partir d'un tableau unidimensionnel avec une longueur de 24 éléments. Tableau B, taille 4 par 6. Si vous regardez l'ordre des valeurs, vous pouvez voir que le long de la deuxième dimension, il y a des chaînes de valeurs séquentielles.
Dans le tableau C, 4 par 3 par 2, les valeurs continues parcourent le dernier axe. Le long du deuxième axe se trouvent des blocs en série, dont la combinaison entraînerait une rangée le long du deuxième axe du réseau B.
Et étant donné que nous n'avons pas fait de copies, il devient clair qu'il s'agit de différentes formes de représentation du même tableau de données. Par conséquent, vous pouvez facilement et rapidement modifier la forme du tableau sans modifier les données elles-mêmes.
Pour connaître la dimension du tableau (nombre d'axes), vous pouvez utiliser le champ ndim (nombre) et connaître la taille le long de chaque axe - forme (tuple). La dimension peut également être reconnue par la longueur de la forme. Pour connaître le nombre total d'éléments dans un tableau, vous pouvez utiliser la valeur de taille:
A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24
Notez que ndim et shape sont des attributs, pas des méthodes!
Pour voir le tableau unidimensionnel, vous pouvez utiliser la fonction Ravel:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6])
Pour redimensionner le long des axes ou de la cote, utilisez la méthode de remodelage:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]])
Il est important que le nombre d'éléments soit préservé. Sinon, une erreur se produira:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3)
Étant donné que le nombre d'éléments est constant, la taille le long de n'importe quel axe lors du remodelage peut être calculée à partir des valeurs de longueur le long d'autres axes. La taille le long d'un axe peut être désignée -1, puis elle sera calculée automatiquement:
A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2)
Vous pouvez utiliser remodeler au lieu de ravel:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,)
Considérez l'application pratique de certaines fonctionnalités pour le traitement d'image. Comme objet de recherche, nous utiliserons une photographie:
Essayons de le télécharger et de le visualiser en utilisant Python. Pour cela, nous avons besoin d'OpenCV et de Matplotlib:
import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show()
Le résultat sera comme ceci:
Faites attention à la barre de téléchargement:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3)
OpenCV fonctionne avec des images au format BGR, et nous connaissons bien le RVB. Nous changeons l'ordre des octets le long de l'axe des couleurs sans accéder aux fonctions OpenCV en utilisant la construction
"[:,:, :: :: 1]".
Réduisez l'image de 2 fois sur chaque axe. Notre image a même des dimensions le long des axes, respectivement, peut être réduite sans interpolation:
I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show()
En changeant la forme du tableau, nous avons obtenu 2 nouveaux axes, 2 valeurs dans chacun, ils correspondent à des cadres composés de lignes et de colonnes impaires et paires de l'image d'origine.
La mauvaise qualité est due à l'utilisation de Matplotlib, car là vous pouvez voir les dimensions axiales. En fait, la qualité de la vignette est:
<up>Réarrangement et transposition des axes
En plus de changer la forme du réseau avec le même ordre d'unités de données, il est souvent nécessaire de changer l'ordre des axes, ce qui entraînera naturellement une permutation des blocs de données.
Un exemple d'une telle transformation est la transposition d'une matrice: échange de lignes et de colonnes.
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6]
Dans cet exemple, la construction AT a été utilisée pour transposer la matrice A. L'opérateur de transposition inverse l'ordre des axes. Prenons un autre exemple avec trois axes:
C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]]
Cette entrée courte a une contrepartie plus longue: np.transpose (A). Il s'agit d'un outil plus polyvalent pour remplacer l'ordre des axes. Le deuxième paramètre vous permet de spécifier un tuple de numéros d'axe du tableau source, qui détermine l'ordre de leur position dans le tableau résultant.
Par exemple, réorganisez les deux premiers axes de l'image. L'image doit basculer, mais laisser l'axe des couleurs inchangé:
I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show()
Pour cet exemple, un autre outil swapaxes pourrait être utilisé. Cette méthode échange les deux axes spécifiés dans les paramètres. L'exemple ci-dessus pourrait être implémenté comme ceci:
I_ = np.swapaxes(I, 0, 1)
<up>Array join
Les tableaux fusionnés doivent avoir le même nombre d'axes. Les tableaux peuvent être combinés avec la formation d'un nouvel axe ou le long d'un axe existant.
Pour se combiner avec la formation d'un nouvel axe, les tableaux originaux doivent avoir les mêmes dimensions sur tous les axes:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]])
Comme vous pouvez le voir dans l'exemple, les tableaux d'opérandes sont devenus des sous-tableaux du nouvel objet et alignés le long du nouvel axe, qui est le tout premier dans l'ordre.
Pour combiner des tableaux le long d'un axe existant, ils doivent avoir la même taille sur tous les axes, sauf celui sélectionné pour la jonction, et ils peuvent avoir des tailles arbitraires le long de celui-ci:
A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]])
Pour combiner le long du premier ou du deuxième axe, vous pouvez utiliser les méthodes vstack et hstack, respectivement. Nous montrons cela avec un exemple d'images. vstack combine des images de la même largeur en hauteur, et hsstack combine les mêmes images en hauteur sur une seule largeur:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show()
Veuillez noter que dans tous les exemples de cette section, les tableaux joints sont transmis par un paramètre (tuple). Le nombre d'opérandes peut être quelconque, mais pas nécessairement seulement 2.
Faites également attention à ce qui arrive à la mémoire lors de la combinaison de tableaux:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]]
Puisqu'un nouvel objet est créé, les données qu'il contient sont copiées à partir des tableaux d'origine, donc les modifications apportées aux nouvelles données n'affectent pas l'original.
<up>Clonage de données
L'opérateur np.repeat (A, n) renverra un tableau unidimensionnel avec des éléments du tableau A, chacun étant répété n fois.
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8]
Après cette conversion, vous pouvez reconstruire la géométrie du tableau et collecter les données en double sur un axe:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]]
Cette option diffère de la combinaison du tableau avec l'opérateur de pile lui-même uniquement à la position de l'axe le long duquel se trouvent les mêmes données. Dans l'exemple ci-dessus, c'est le dernier axe, si vous utilisez stack - le premier:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]]
Quelle que soit la façon dont les données sont clonées, l'étape suivante consiste à déplacer l'axe le long duquel les mêmes valeurs se trouvent à n'importe quelle position avec le système d'axes:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]]
Si nous voulons «étirer» n'importe quel axe en utilisant la répétition des éléments, alors l'axe avec les mêmes valeurs doit être placé
après l' expansible (en utilisant la transposition), puis combiner ces deux axes (en utilisant le remodelage). Prenons un exemple d'étirement d'une image le long d'un axe vertical en dupliquant des lignes:
I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1]
<up>Opérations mathématiques sur les éléments du tableau
Si A et B sont des tableaux de même taille, ils peuvent être ajoutés, multipliés, soustraits, divisés et élevés à une puissance. Ces opérations sont effectuées
élément par élément , le tableau résultant coïncidera en géométrie avec les tableaux d'origine, et chacun de ses éléments sera le résultat de l'opération correspondante sur une paire d'éléments des tableaux d'origine:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]]
Vous pouvez effectuer n'importe quelle opération de ce qui précède sur le tableau et le numéro. Dans ce cas, l'opération sera également effectuée sur chacun des éléments du tableau:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]]
En considérant qu'un tableau multidimensionnel peut être considéré comme un tableau plat (premier axe), dont les éléments sont des tableaux (autres axes), il est possible d'effectuer les opérations considérées sur les tableaux A et B dans le cas où la géométrie B coïncide avec la géométrie des sous-réseaux A avec une valeur fixe le long du premier axe . En d'autres termes, avec le même nombre d'axes et de tailles A [i] et B. Dans ce cas, chacun des tableaux A [i] et B sera des opérandes pour les opérations définies sur les tableaux.
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]]
Dans cet exemple, le tableau B est soumis à une opération avec chaque ligne du tableau A. Si vous devez multiplier / diviser / ajouter / soustraire / augmenter le degré de sous-réseaux le long d'un autre axe, vous devez utiliser la transposition pour placer l'axe souhaité à sa première place, puis le remettre à sa place. Considérez l'exemple ci-dessus, mais avec la multiplication par le vecteur B des colonnes du tableau A:
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]]
Pour les fonctions plus complexes (par exemple, trigonométrique, exposant, logarithme, conversion entre degrés et radians, module, racine carrée, etc.), NumPy a une implémentation. Prenons l'exemple de l'exponentiel et du logarithme: A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]]
Une liste complète des opérations mathématiques dans NumPy peut être trouvée ici .<up>Multiplication matricielle
L'opération ci-dessus du produit des matrices est effectuée élément par élément. Et si vous devez effectuer des opérations selon les règles de l'algèbre linéaire sur les tableaux comme sur les tenseurs, vous pouvez utiliser la méthode point (A, B). Selon le type d'opérandes, la fonction effectuera:- si les arguments sont des scalaires (nombres), alors la multiplication sera effectuée;
- si les arguments sont un vecteur (tableau unidimensionnel) et un scalaire, alors le tableau sera multiplié par un nombre;
- si les arguments sont vectoriels, alors une multiplication scalaire sera effectuée (la somme des produits par élément);
- si les arguments sont tensor (tableau multidimensionnel) et scalaire, alors le vecteur sera multiplié par un nombre;
- si les arguments du tenseur, alors le produit des tenseurs le long du dernier axe du premier argument et de l'avant-dernier - second sera exécuté;
- si les arguments sont des matrices, alors le produit des matrices est exécuté (c'est un cas particulier du produit des tenseurs);
- si les arguments sont matrice et vecteur, alors le produit de la matrice et du vecteur sera exécuté (c'est aussi un cas particulier du produit des tenseurs).
Pour effectuer les opérations, les tailles correspondantes doivent coïncider: pour les vecteurs de longueur, pour les tenseurs, les longueurs le long des axes le long desquels les produits par élément seront additionnés.Prenons des exemples avec des scalaires et des vecteurs:
Avec les tenseurs, nous verrons seulement comment la géométrie du tableau résultant change de taille:
Pour effectuer un produit tensoriel en utilisant d'autres axes, au lieu de ceux définis pour le point, vous pouvez utiliser tensordot avec un axe explicite: A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8)
Nous avons explicitement indiqué que nous utilisons le troisième axe du premier tableau et le deuxième - du second (les tailles le long de ces axes doivent correspondre).<up>Agrégateurs
Les agrégateurs sont des méthodes NumPy qui vous permettent de remplacer des données par des caractéristiques intégrales le long de certains axes. Par exemple, vous pouvez calculer la valeur moyenne, le maximum, le minimum, la variation ou une autre caractéristique le long d'un ou de plusieurs axes et former un nouveau tableau à partir de ces données. La forme du nouveau tableau contiendra tous les axes du tableau d'origine, à l'exception de ceux le long desquels l'agrégateur a été compté.Pour un exemple, nous allons former un tableau avec des valeurs aléatoires. Ensuite, nous trouvons la valeur minimale, maximale et moyenne dans ses colonnes: A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039]
Avec cette utilisation, les moyennes et moyennes ressemblent à des synonymes. Mais ces fonctions ont un ensemble différent de paramètres supplémentaires. Il existe différentes possibilités pour masquer et pondérer les données moyennes.Vous pouvez calculer les caractéristiques intégrales sur plusieurs axes: A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
Dans cet exemple, une autre somme caractéristique intégrale est considérée - la somme.La liste des agrégateurs ressemble à ceci:- sum: sum et nansum - une variante qui se gère correctement avec nan;
- travail: prod et nanprod;
- moyenne et attente: moyenne et moyenne (nanmean),
il n'y a pas de moyenne nanométrique ; - médiane: médiane et nanmédiane;
- percentile: percentile et nanpercentile;
- variation: var et nanvar;
- écart-type (racine carrée de la variation): std et nanstd;
- : min nanmin;
- : max nanmax;
- , : argmin nanargmin;
- , : argmax nanargmax.
Dans le cas de l'utilisation d'argmin et d'argmax (respectivement, nanargmin et nanargmax), vous devez spécifier un axe le long duquel la caractéristique sera prise en compte.Si vous ne spécifiez pas d'axe, par défaut, toutes les caractéristiques prises en compte sont prises en compte dans l' ensemble du tableau. Dans ce cas, argmin et argmax fonctionnent également correctement et trouvent l'index de l'élément maximum ou minimum, comme si toutes les données du tableau étaient étirées le long du même axe avec la commande ravel ().Il convient également de noter que les méthodes d'agrégation sont définies non seulement comme des méthodes du module NumPy, mais aussi pour les tableaux eux-mêmes: l'entrée np.aggregator (A, axes) est équivalente à l'entrée A.aggregator (axes), où agrégateur signifie l'une des fonctions considérées ci-dessus, et axes - indices d'axe. A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
<up>Au lieu d'une conclusion - un exemple
Construisons un algorithme pour le filtrage linéaire des images passe-bas.Pour commencer, téléchargez une image bruyante.
Considérons un fragment de l'image pour voir le bruit:
nous filtrerons l'image à l'aide d'un filtre gaussien. Mais au lieu d'effectuer la convolution directement (avec itération), nous appliquons la moyenne pondérée des tranches d'image décalées les unes par rapport aux autres: def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J
Nous appliquons cette fonction à notre image une, deux fois et trois fois: I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3)
On obtient les résultats suivants:
avec une seule utilisation du filtre;
avec double;
à trois reprises.On peut voir qu'avec une augmentation du nombre de passages de filtre, le niveau de bruit diminue. Mais cela réduit également la clarté de l'image. Il s'agit d'un problème connu avec les filtres linéaires. Mais notre méthode de débruitage d'image ne prétend pas être optimale: ce n'est qu'une démonstration des capacités de NumPy à implémenter la convolution sans itérations.Voyons maintenant la convolution avec laquelle les noyaux de notre filtrage sont équivalents. Pour ce faire, nous soumettrons une impulsion d'unité unique à des transformations similaires et visualiserons. En fait, l'impulsion ne sera pas unique, mais égale en amplitude à 255, car le mélange lui-même est optimisé pour les données entières. Mais cela n'interfère pas avec l'évaluation de l'aspect général des noyaux: M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show()
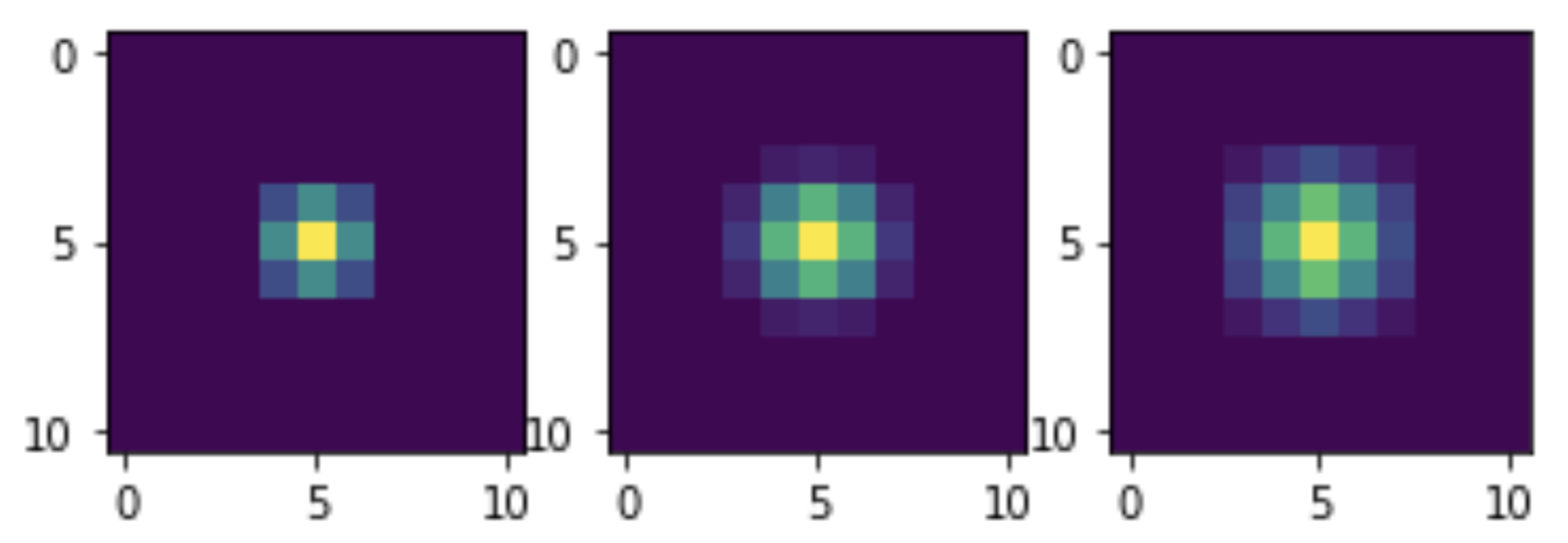Nous avons considéré un ensemble loin d'être complet de fonctionnalités NumPy, j'espère que cela a suffi pour démontrer toute la puissance et la beauté de cet outil!<up>