Dans cet article, nous parlerons du nouveau langage JetBrains avec les types dépendants d'Arend (le langage est nommé d'après
Gating Rent ). Ce langage a été développé par
JetBrains Research au cours des dernières années. Bien que les dépôts il y a un an aient été rendus publics sur
github.com/JetBrains , la version complète d'Arend n'est arrivée qu'en juillet de cette année.
Nous allons essayer de dire en quoi Arend diffère des systèmes existants de mathématiques formalisées basées sur des types dépendants, et quelles fonctionnalités sont désormais disponibles pour ses utilisateurs. Nous supposons que le lecteur de cet article est généralement familier avec les types dépendants et a entendu au moins une des langues basées sur les types dépendants: Agda, Idris, Coq ou Lean. Cependant, nous ne nous attendons pas à ce que le lecteur ait des types dépendants à un niveau avancé.
Pour plus de simplicité et de concrétisation, notre histoire sur les types Arend et homotopie sera accompagnée de l'implémentation sur Arend de l'algorithme de tri de liste le plus simple - même avec cet exemple, vous pouvez sentir la différence entre Arend et Agda et Coq. Il existe déjà un certain nombre d'articles sur Habré consacrés aux types dépendants. Disons que l'implémentation de listes de tri à l'aide de la méthode QuickSort sur Agda existe
un tel article . Nous allons implémenter un algorithme plus simple pour trier les inserts. Dans ce cas, nous nous concentrerons sur les constructions du langage Arend, et non sur l'algorithme de tri lui-même.
Ainsi, la principale différence entre Arend et d'autres langages à types dépendants est la théorie logique sur laquelle il est basé. Arend utilise à ce titre la théorie du type d'homotopie
V. Hoevodsky récemment découverte (
HoTT ). Plus précisément, Arend est basé sur une variation de HoTT appelée «théorie des types avec espacement». Rappelons que Coq est basé sur le soi-disant calcul des constructions inductives (Calcul des constructions inductives), tandis que Agda et Idris sont basés sur la
théorie intensionnelle des types de Martin-Löf . Le fait qu'Arend soit basé sur HoTT affecte de manière significative ses constructions syntaxiques et le fonctionnement de l'algorithme de vérification de type (typcheker). Nous allons discuter de ces fonctionnalités dans cet article.
Essayons de décrire brièvement l'état de l'infrastructure linguistique. Pour Arend, il existe un plugin pour IntelliJ IDEA, qui peut être installé directement à partir du référentiel des plugins IDEA. En principe, l'installation du plugin est suffisante pour fonctionner pleinement avec Arend, vous n'avez toujours pas besoin de télécharger et d'installer quoi que ce soit. En plus de la vérification de type, le plugin Arend fournit des fonctionnalités familières aux utilisateurs d'IDEA: il y a la mise en évidence et l'alignement du code, divers refactorings et conseils. Il existe également la possibilité d'utiliser la version console d'Arend. Une description plus détaillée du processus d'installation peut être trouvée
ici .
Les exemples de code de cet article sont basés sur la bibliothèque standard d'Arend, nous vous recommandons donc de télécharger son code source à partir du
référentiel . Après le téléchargement, le répertoire source doit être importé en tant que projet IDEA à l'aide de la commande Importer un projet. À Arend, certaines sections de la théorie des types d'homotopie et de la théorie des anneaux ont déjà été formalisées. Par exemple, dans la bibliothèque standard, il y a une implémentation de l'anneau de nombres rationnels Q avec des preuves de toutes les propriétés théoriques de l'anneau requises.
Une
documentation linguistique détaillée, dans laquelle de nombreux points abordés dans cet article sont expliqués plus en détail, est également du domaine public. Vous pouvez directement poser des questions aux développeurs Arend sur le
canal télégramme .
1. Présentation de HoTT / Arend
La théorie de type homotopie (ou, en bref, HoTT) est un type de théorie de type intensionnel qui diffère de la théorie de type classique de Martin-Löf (MLTT, sur laquelle Agda est basée) et du calcul de construction inductive (CIC, sur lequel Coq est basé), en ce que, avec les instructions et les ensembles contiennent les soi-disant types d'un niveau d'homotopie supérieur.
Dans cet article, nous ne nous fixons pas l'objectif d'expliquer en détail les fondements de HoTT - pour une exposition détaillée de cette théorie, il serait nécessaire de relire l'intégralité du livre (voir
cet article ). On constate seulement qu'une théorie basée sur l'axiomatique de HoTT est, en un sens, beaucoup plus élégante et intéressante que la théorie classique de type Martin-Löf. Ainsi, un certain nombre d'axiomes qui devaient auparavant être postulés en plus (par exemple, l'extensionnalité fonctionnelle) sont prouvés dans HoTT comme théorèmes. De plus, dans HoTT, on peut définir en interne des sphères d'homotopie multidimensionnelles et même compter certains de leurs
groupes d'homotopie .
Cependant, ces aspects de HoTT sont principalement intéressants pour les mathématiciens, et le but de cet article est d'expliquer comment l'Arend basé sur HoTT se compare favorablement avec Agda / MLTT et Coq / CIC par l'exemple de la représentation aussi simple et familière à toute entité de programmeur que des listes ordonnées. À la lecture de cet article, il suffit de traiter HoTT comme une sorte de théorie de type intensionnelle avec une axiomatique plus développée, ce qui est pratique lorsque l'on travaille avec des univers et des égalités.
1.1 Types dépendants, correspondance Curry-Howard, univers
Rappelons que les langages avec des types dépendants diffèrent des langages de programmation fonctionnels ordinaires en ce qu'en plus des types de données habituels, tels que les listes ou les nombres naturels, il existe des types en fonction de la valeur du paramètre. Les exemples les plus simples de ces types sont des vecteurs d'une longueur donnée n ou des arbres équilibrés d'une profondeur donnée d. Quelques autres exemples de ces types sont mentionnés
ici.Rappelons que la
correspondance Curry-Howard permet d'interpréter les énoncés de logique comme des types dépendants. L'idée principale de cette correspondance est qu'un type vide correspond à une fausse déclaration et que les types remplis correspondent à une vraie déclaration. Les éléments de type peuvent être considérés comme des preuves de l'énoncé logique correspondant. Par exemple, tout élément tel que des entiers peut être considéré comme une preuve du fait que des entiers existent (c'est-à-dire que le type d'entiers est renseigné).
Différentes constructions naturelles sur les types correspondent à différents connecteurs logiques:
- Le produit des types A × B est parfois appelé le type d'une paire Pair A B. Puisque ce type est rempli si et seulement si les deux types A et B sont remplis, cette construction correspond au «et» logique.
- La somme des types A + B. Dans Haskell, ce type est appelé Soit A B. Puisque ce type est rempli si et seulement si l'un des types A ou B est rempli, cette construction correspond à un «ou» logique.
- Type fonctionnel A → B. Toute fonction de ce type convertit les éléments de A en éléments de B. Ainsi, une telle fonction existe exactement lorsque l'existence d'un élément de type A implique l'existence d'un élément de type B. Par conséquent, cette construction correspond à l'implication.
Supposons maintenant que l'on nous donne un certain type A et une famille de types B paramétrés par un élément a de type A. Donnons des exemples de constructions plus complexes sur des types dépendants.
- Type de fonction dépendante Π (a: A) (B a). Ce type coïncide avec le type fonctionnel habituel A → B si B est indépendant de A. Une fonction de type Π (a: A) (B a) convertit tout élément a de type A en élément de type B a. Ainsi, une telle fonction existe si et seulement si, pour tout a : A, il existe un élément B a. Par conséquent, cette construction correspond au quantificateur universel ∀. Pour le type fonctionnel dépendant, Arend utilise la syntaxe
\Pi (x : A) -> B a , et le terme habitant ce type peut être construit en utilisant l'expression lambda \lam (a : A) => f a. - Le type de paires dépendantes est Σ (a: A) (B a). Ce type coïncide avec les types habituels de paires A × B si B est indépendant de A. Le type Σ (a: A) (B a) est rempli exactement lorsqu'il existe un élément a: A et un élément de type B a. Ainsi, ce type correspond au quantificateur d'existence
∃ . Le type de paires dépendantes dans Arend est désigné par \Sigma (a : A) (B a) , et les termes qui les habitent sont construits en utilisant le constructeur de la paire (a, b) dépendante) (a, b) .
- Le type d'égalité est a = a ', où a et a' sont deux éléments d'un certain type A. Un tel type est rempli si a et a 'sont égaux, et est vide sinon. Évidemment, ce type est un analogue du prédicat d'égalité en logique.
À ce stade, nous renvoyons le lecteur à des sources dans lesquelles la correspondance Curry-Howard est discutée plus en détail (voir, par exemple, un
cours magistral ou des articles
ici ou
ici ).
Toutes les expressions considérées dans la théorie des types doivent avoir un certain type. Étant donné que les expressions désignant des types sont également considérées dans le cadre de cette théorie, elles doivent également être affectées à un certain type. La question est, quel type de type devrait-il être?
La première décision naïve qui vient à l'esprit est d'assigner à tous les types un type formel
\Type , appelé l'
univers (il est ainsi appelé parce qu'il contient tous les types en général). Si nous utilisons cet univers, les constructions de somme et les produits de type mentionnés ci-dessus recevront la signature
\Type → \Type → \Type , et les constructions plus complexes du produit dépendant et la somme dépendante recevront la signature
Π (A : \Type) → ((A → \Type) → \Type) .
À ce stade, la question se pose: quel type doit avoir l'univers
\Type lui-même? Une tentative naïve de dire que le type de l'univers
\Type , par définition, est
\Type lui-même conduit au
paradoxe Girard , donc au lieu d'un seul univers
\Type considérons une
hiérarchie infinie
d'univers , c'est-à-dire la chaîne imbriquée d'univers
\Type 1 < \Type 2 < … , dont les niveaux sont numérotés par des nombres naturels, et le type de l'univers
\Type i , par définition, est l'univers
\Type (i+1) . Pour les constructions de type mentionnées ci-dessus,
des signatures plus
complexes doivent également être introduites.
Ainsi, les univers en théorie des types sont nécessaires pour que toute expression ait un certain type. Dans certaines variétés de théorie des types, les univers sont utilisés dans un autre but: distinguer les variétés de types. Nous avons déjà vu que les ensembles et les instructions sont des cas particuliers de types. Cela montre qu'il pourrait être judicieux d'introduire dans la théorie un univers Prop distinct pour les instructions et une hiérarchie distincte des univers Set
i pour les ensembles. C'est exactement l'approche utilisée dans le Calcul des constructions inductives, la théorie sur laquelle le système Coq est basé.
1.2 Exemples de types inductifs et de fonctions récursives les plus simples
Considérez les définitions sur Arend des types de données inductifs les plus simples: type booléen, type de nombre naturel et listes polymorphes. Arend utilise le mot-clé
\data pour introduire de nouveaux types inductifs.
\data Empty -- ,
\data Bool
| true
| false
\data Nat
| zero
| suc Nat
\data List (A : \Set)
| nil
| \infixr 5 :-: A (List A)Comme vous pouvez le voir dans les exemples ci-dessus, après le mot-clé
\data , vous devez spécifier le nom du type inductif et une liste de ses constructeurs. Dans le même temps, le type de données et les constructeurs peuvent avoir certains paramètres. Disons que dans l'exemple ci-dessus, le type
List a un paramètre
A Le constructeur de liste
nil n'a pas de paramètres, et le constructeur: -: a deux paramètres (dont l'un est de type
A et l'autre est de type
List A ). L'univers
\Set compose de types qui sont des ensembles (la définition des ensembles sera donnée dans la section suivante). Le
\infixr vous permet d'utiliser la notation infixe pour le constructeur: -: et, en outre, indique à l'analyseur Arend que l'opérateur: -: est une opération associative à droite avec la priorité 5.
Dans Arend, tous les mots clés commencent par un caractère barre oblique inverse («\»), une implémentation inspirée de LaTeX. Notez simplement que les règles lexicales d'Arend sont très libérales:
Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left et même
n:Nat - tous ces littéraux sont des exemples d'identifiants valides dans Arend. Le dernier exemple montre à quel point il est important pour l'utilisateur Arend
de se rappeler de mettre des espaces entre les identifiants et les deux points . Notez que dans les identifiants Arend, il n'est pas autorisé d'utiliser des caractères Unicode (en particulier, vous ne pouvez pas utiliser le cyrillique).
Arend utilise le mot clé
\func pour définir les fonctions. La syntaxe de cette construction est la suivante: après le mot-clé
\func , vous devez spécifier le nom de la fonction, ses paramètres et le type de la valeur de retour. Le dernier élément dans la définition d'une fonction est son corps.
S'il est possible de spécifier explicitement l'expression dans laquelle la fonction donnée doit être calculée, alors pour indiquer le corps de la fonction, le jeton => est utilisé. Considérons, par exemple, la définition d'une fonction de négation de type.
\func Not (A : \Type) : \Type => A -> Empty
Le type de retour d'une fonction ne doit pas toujours être spécifié explicitement. Dans l'exemple ci-dessus, Arend serait en mesure de déduire indépendamment le type
Not , et nous pourrions omettre l'expression «:
\Type » après les crochets.
Comme dans la plupart des systèmes mathématiques formalisés, l'utilisateur n'a pas à indiquer un niveau prédictif explicite dans l'univers
\Type , et les définitions dans lesquelles les univers sont utilisés sans spécifier explicitement un niveau prédictif sont considérées comme
polymorphes .
Essayons maintenant de définir une fonction qui calcule la longueur de la liste. Une telle fonction est facile à identifier grâce à la correspondance de motifs. Arend utilise pour cela le mot-clé
\elim . Après cela, vous devez spécifier les variables par lesquelles la comparaison est effectuée (s'il existe plusieurs variables de ce type, elles doivent être écrites avec une virgule). Si la comparaison est effectuée pour tous les paramètres explicites, alors
\elim ainsi que les variables peuvent être omis. Il est suivi d'un bloc de points de comparaison, séparés les uns des autres par une barre verticale "|". Chaque élément de ce bloc est une expression de la forme
«, » => «» .
\func length {A : \Set} (l : List A) : Nat | nil => 0 | :-: x xs => suc (length xs)
Dans l'exemple ci-dessus, le paramètre A de la fonction de
length est entouré d'accolades. Ces crochets dans Arend sont utilisés pour désigner des arguments implicites, c'est-à-dire arguments que l'utilisateur peut omettre lors de l'appel d'une fonction ou de l'utilisation d'un type. Notez que dans Arend, vous ne pouvez pas utiliser la notation infixe pour désigner les constructeurs lors de la correspondance avec un modèle, de sorte que la notation préfixe est utilisée dans l'exemple d'exemple.
Comme dans Coq / Agda, dans Arend, toutes les fonctions doivent être garanties d'être terminées (c'est-à-dire que la vérification de terminaison est présente dans Arend). Dans la définition de la fonction de longueur, cette vérification est réussie, car un appel récursif réduit strictement le premier argument explicite. Si une telle réduction ne se produisait pas, Arend enverrait un message d'erreur.
\func bad : Nat => bad [ERROR] Termination check failed for function 'bad' In: bad
Arend permet des dépendances circulaires et des fonctions mutuellement récursives pour lesquelles des contrôles d'achèvement sont également effectués. L'algorithme de cette vérification est implémenté sur la base de l'
article de A. Abel. Vous y trouverez une description plus détaillée des conditions que les fonctions mutuellement récursives doivent remplir.
1.3 En quoi les ensembles diffèrent-ils des énoncés?
Nous avons précédemment écrit que des exemples de types sont des ensembles et des instructions. De plus, nous avons utilisé les mots clés
\Type et
\Set pour désigner les univers dans Arend. Dans cette section, nous allons essayer d'expliquer plus en détail en quoi les énoncés diffèrent des ensembles en termes de variétés de la théorie des types intensionnels (MLTT, CIC, HoTT), et en même temps expliquer en quoi consiste la signification des mots clés
\Prop ,
\Set et
\Type dans Arend.
Rappelons que dans la théorie classique de Martin-Löf, il n'y a pas de séparation des types en ensembles et en énoncés. En particulier, en théorie, il n'y a qu'un seul univers cumulatif (qui est désigné par Set in Agda, ou Type in Idris, ou Sort in Lean). Cette approche est la plus simple, mais il existe des situations où ses lacunes se manifestent. Supposons que nous essayons d'implémenter le type "liste ordonnée" comme une paire dépendante composée d'une liste et d'une preuve de son ordre. Il s'avère alors que, dans le cadre du MLTT «pur», il ne sera pas possible de prouver l'égalité des listes ordonnées constituées d'éléments identiques, qui en même temps diffèrent en termes de preuve de commande. Avoir une telle égalité serait très naturel et souhaitable, de sorte que l'impossibilité de la prouver peut être considérée comme un défaut théorique du MLTT.
Dans Agda, ce problème est partiellement résolu à l'aide de ce que l'on appelle des annotations d'immatérialité (voir la
source , dans laquelle l'exemple de liste est discuté plus en détail). Ces annotations, cependant, ne sont pas une construction de la théorie MLTT, ni des constructions à part entière sur des types (il est impossible de marquer avec une annotation de type qui n'est pas utilisée dans l'argument de fonction).
Dans CIC, basé sur CIC, il existe deux univers différents imbriqués l'un dans l'autre:
Prop (l'univers des énoncés) et
Set (l'univers des ensembles), qui sont immergés dans la hiérarchie complète des univers
Type . La principale différence entre
Prop et
Set est qu'il existe un certain nombre de restrictions sur les variables dont le type appartient à
Prop dans Coq. Par exemple, ils ne peuvent pas être utilisés dans les calculs et leur comparaison avec l'échantillon n'est possible qu'à l'intérieur des preuves d'autres déclarations. D'autre part, tous les éléments du type appartenant à l'univers
Prop sont égaux dans l'axiome de la preuve sans conséquence, voir la déclaration dans
Coq.Logic.ProofIrrelevance . En utilisant cet axiome, nous pourrions facilement prouver l'égalité des listes ordonnées mentionnées ci-dessus.
Enfin, considérons l'approche Arend / HoTT des déclarations et des univers. La principale différence est que HoTT renonce à l'axiome de la preuve sans conséquence. Autrement dit, il n'y a pas d'axiome spécial dans HoTT qui postule que tous les éléments des déclarations sont égaux. Mais dans HoTT, un type,
par définition , est une déclaration s'il peut être prouvé que tous ses éléments sont égaux les uns aux autres. Nous pouvons définir un prédicat sur les types qui est vrai si le type est une instruction:
\func isProp (A : \Type) => \Pi (aa' : A) -> a = a'
La question se pose: quels types satisfont ce prédicat, c'est-à-dire, sont des déclarations? Il est facile de vérifier que cela est vrai pour les types vides et singleton. Pour les types où il y a au moins deux éléments différents, cela ne sera plus vrai.
Bien sûr, nous voulons que tous les connecteurs logiques nécessaires soient définis sur les instructions. Dans la section 1.1, nous avons déjà discuté de la façon dont ils pouvaient être déterminés à l'aide de constructions théoriques de type. Il y a cependant le problème suivant: toutes les opérations que nous avons saisies ne conservent pas la propriété
isProp . Les constructions du produit des types et du type fonctionnel (dépendant) conservent cette propriété, contrairement aux constructions de la somme des types et des paires dépendantes. Ainsi, nous ne pouvons pas utiliser la disjonction et le quantificateur d'existence.
Ce problème peut être résolu à l'aide d'une nouvelle construction, qui est ajoutée à HoTT, la soi-disant
troncature propositionnelle . Cette conception vous permet de transformer n'importe quel type en déclaration. Elle peut être considérée comme une opération formelle, égalisant tous les termes qui habitent ce type. Cette opération est quelque peu similaire aux annotations d'immatérialité d'Agda, cependant, contrairement à elles, c'est une opération à part entière sur les types avec signature
\Type -> \Prop .
Le dernier exemple important d'instructions est l'égalité de deux éléments d'un certain type. Il s'avère que dans le cas général, le type d'égalité
a = a' ne doit pas nécessairement être une déclaration. Les types pour lesquels il s'agit d'un sont appelés ensembles:
\func isSet (A : \Type) => \Pi (aa' : A) -> isProp (a = a')
Tous les types que l'on trouve dans les langages de programmation ordinaires satisfont à ce prédicat, c'est-à-dire que l'égalité sur eux est une déclaration. Par exemple, cela est vrai pour les nombres naturels, les entiers, les produits d'ensembles, les sommes d'ensembles, les fonctions sur les ensembles, les listes d'ensembles et d'autres types de données inductives construits à partir d'ensembles. Cela signifie que si nous ne sommes intéressés que par de telles constructions familières, nous ne pouvons pas penser à des types arbitraires qui ne satisfont pas ce prédicat. Tous les types trouvés dans Coq sont des
ensembles .
Les types qui ne sont pas des ensembles deviennent utiles si vous voulez traiter de la théorie des types d'homotopie. Pour l'instant, nous renvoyons simplement le lecteur au
module de bibliothèque standard contenant la définition d'une
sphère à n dimensions , un exemple d'un type qui n'est pas un ensemble.
Arend a des univers spéciaux
\Prop et
\Set , constitués respectivement d'instructions et d'ensembles. Si nous savons déjà que le type A est contenu dans l'univers
\Prop (ou
\Set ), alors la preuve de la
isProp (ou
isSet ) correspondante dans Arend peut être obtenue en utilisant l'axiome
Path.inProp intégré au
prélude (nous donnons un exemple d'utilisation de cet axiome dans la section 2.3).
\func inProp {A : \Prop} : \Pi (aa' : A) -> a = a'
Nous avons déjà noté que toutes les constructions naturelles sur les types ne conservent pas la propriété
isProp . Par exemple, les types de données inductifs avec deux ou plusieurs constructeurs ne le satisfont jamais. Comme indiqué ci-dessus, nous pouvons utiliser la construction de
troncature propositionnelle qui transforme n'importe quel type en instruction.
Dans la bibliothèque Arend, l'implémentation standard de la troncature propositionnelle est appelée
Logic.TruncP . On pourrait définir un type de «ou» logique dans Arend comme tronquant la somme des types:
\data \fixr 2 Or (AB : \Type) -- Sum of types; analogue of Coq's type "sum" | inl A | inr B \func \infixr 2 || (AB : \Type) => TruncP (sum AB) -- Logical “or”, analogue of Coq's type "\/"
Dans Arend, il existe un autre moyen plus simple et plus pratique de définir un type inductif tronqué propositionnellement. Pour ce faire, ajoutez simplement le mot clé
\truncated avant de définir le type de données. Par exemple, la définition d'un «ou» logique dans la bibliothèque standard Arend est donnée comme suit.
\truncated \data \infixr 2 || (AB : \Type) : \Prop -- Logical “or”, analogue of Coq's type "\/" | byLeft A | byRight B
Les travaux ultérieurs avec des types tronqués propositionnellement ressemblent à ceux des types assignés à l'univers
Prop dans Coq. Par exemple, la correspondance de modèle d'une variable dont le type est une instruction n'est autorisée que dans une situation où le type de l'expression définie est lui-même une instruction. Ainsi, il est toujours facile de définir la fonction
Or-to-|| par comparaison avec l'échantillon, mais la fonction inverse, uniquement si le type A
`Or` B est une instruction (ce qui est assez rare, par exemple, lorsque les types
A et
B sont tous deux des instructions et s'excluent mutuellement).
\func Or-to-|| {AB : \Prop} (a-or-b : A `Or` B) : A || B | inl a => byLeft a | inr b => byRight
Rappelons également que la particularité du mécanisme des univers dans Coq est que si une définition a été assignée à l'univers
Prop , il ne sera en aucun cas possible de l'utiliser dans le calcul. Pour cette raison, les développeurs de Coq eux
- mêmes
ne recommandent pas l' utilisation de constructions propositionnelles, mais conseillent de les remplacer par des analogues de l'univers des ensembles, si possible. Le mécanisme des univers Arend ne présente pas cet inconvénient, c'est-à-dire que dans certaines situations, il est possible d'utiliser des instructions dans les calculs. Nous donnerons un exemple d'une telle situation lorsque nous discuterons de la mise en œuvre de l'algorithme de tri de liste.
1.4 Classes à Arend
Notre objectif étant d'implémenter l'algorithme de tri le plus simple, il semble utile de vous familiariser avec l'implémentation des ensembles ordonnés disponibles dans la bibliothèque standard d'Arend.
Dans Arend, les classes sont utilisées pour encapsuler les opérations et les axiomes qui définissent les structures mathématiques, ainsi que pour mettre en évidence les relations entre ces structures à l'aide de l'héritage. Les classes sont également des espaces de noms, à l'intérieur desquels il est commode de placer des constructions et des théories qui ont un sens approprié.
La classe de base dont toutes les classes d'ordre dans Arend sont héritées est la classe
BaseSet , qui ne contient aucun membre autre que la désignation
E pour l'ensemble hôte (c'est-à-dire l'ensemble sur lequel les
BaseSet descendantes
BaseSet introduisent déjà diverses opérations). Considérez la définition de cette classe à partir de la bibliothèque Arend standard.
\class BaseSet (E : \Set) -- ,
Dans la définition ci-dessus, la porteuse
E déclarée paramètre de classe. On peut se demander s'il existe une différence entre la définition de
BaseSet ci-dessus et la définition suivante, dans laquelle l'opérateur E est défini comme un champ de classe?
\class BaseSet' -- | E : \Set
Une réponse légèrement inattendue est que dans Arend
il n'y a pas de différence entre les deux définitions dans le sens où tout paramètre de classe (même implicite) dans Arend est, en fait, son champ. Ainsi, pour les deux implémentations de
BaseSet , on pourrait utiliser l'expression
xE pour accéder au champ E.
BaseSet toujours une différence entre les variantes ci-dessus de la définition de
BaseSet , mais elle est plus subtile, nous l'examinerons plus en détail dans la section suivante lorsque nous discuterons des instances de classe ( instances de classe).
L'opération de tri d'une liste n'a de sens que si un ordre linéaire est spécifié sur le type d'objets dans la liste.Par conséquent, nous considérons d'abord les définitions d'un
ensemble partiellement ordonné strict et d'un
ensemble ordonné linéairement. \class StrictPoset \extends BaseSet { | \infix 4 < : E -> E -> \Prop | <-irreflexive (x : E) : Not (x < x) | <-transitive (xyz : E) : x < y -> y < z -> x < z } \class LinearOrder \extends StrictPoset { | <-comparison (xyz : E) : x < z -> x < y || y < z | <-connectedness (xy : E) : Not (x < y) -> Not (y < x) -> x = y }
Du point de vue de la théorie des types, les classes dans Arend peuvent être considérées comme des analogues des types sigma avec une syntaxe plus pratique pour les projections et les constructeurs. , Arend- -, .
,
. , . , StrictPoset
<-irreflexive <-transitive ,
E < — . , (, , ) , .
, , . , Arend
, , . , . , , , , .
:
\class DecSet \extends BaseSet | decideEq (xy : E) : Dec (x = y)
Dec ,
Dec E ,
E ,
E ,
E .
\data Dec (E : \Prop) | yes E | no (Not E)
, ,
Dec ( decidable)
Order.LinearOrder . Dec , , ,
trichotomy , ,
E , <. ,
Dec Comparable Java.
\class Dec \extends LinearOrder, DecSet { | trichotomy (xy : E) : (x = y) || (x < y) || (y < x) | <-comparison xyz x<z => {?} -- | <-connectedness xyx/<yy/<x => {?} | decideEq xy => {?} }
Dec Dec , , , , .
Dec , .
,
Dec ( ).
Dec , Arend (
Dec LinearOrder, DecSet ), , (diamond inheritance).
: , ( , ).
Dec Order.LinearOrder IDEA ( [Ctrl]+[H]), , .
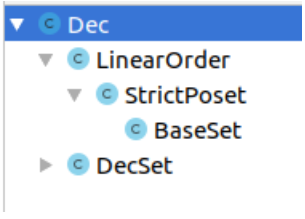
Arend ( IDEA
BaseSet ). , .
1.5 , , .
StrictPoset Nat. Arend , . -, , , - ( ), .
: . .
data \infix 4 < (ab : Nat) \with | zero, suc _ => zero<suc_ | suc a, suc b => suc<suc (a < b) \lemma irreflexivity (x : Nat) (p : x < x) : Empty | suc a, suc<suc a<a => irreflexivity a a<a \lemma transitivity (xyz : Nat) (p : x < y) (q : y < z) : x < z | zero, suc y', suc z', zero<suc_, suc<suc y'<z' => zero<suc_ | suc x', suc y', suc z', suc<suc x'<y', suc<suc y'<z' => suc<suc (transitivity x' y' z' x'<y' y'<z')
\func \lemma . , , , . ,
\lemma ,
\Prop .
x'<y' — -,
x' < y' . - (.. , , ).
(instance)
StrictPoset. Arend a plusieurs options de syntaxe différentes pour cela. La première façon d'instancier une classe est d'utiliser un mot-clé \newdans n'importe quelle expression. Dans ce cas, une «instance de classe anonyme» sera créée. \func NatOrder => \new StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
StrictPoset { … } \new : -
StrictPoset . - , , ,
\new .
\new C { … } C { … } . C, C. , ,
NatOrder StrictPoset .
, . ,
StrictPoset Nat StrictPoset { | E => Nat } . ,
NatOrder StrictPoset , ( ).
NatOrder \cowith ( - ).
\func NatOrder : StrictPoset \cowith { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
, ,
\instance. \instance NatOrder : StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity }
Arend , Haskell.
NatOrder \instance \cowith ,
StrictPoset ( ).
,
BaseSet - E ( ), , E . .
, Arend . Arend , , ( , «
»
\classifying \field , Arend ). :
- Arend . ,
X StrictPoset , List X List XE .
- Arend .
, . ,
\instance StrictPoset ,
Nat Int (
NatOrder IntOrder ).
,
x < y , x, y , , x, y . Arend ,
NatOrder.< , —
IntOrder.< .
, . Arend , <
StrictPoset , E. , Arend
x<y StrictPoset ( ), E . ,
< .
, Arend. ,
\use \coerce . Arend
— , , . - ,
\where .
.
fromNat .
\data Int | pos Nat | neg Nat \with { zero => pos zero } \where { \use \coerce fromNat (n : Nat) => pos n }
\use \coerce \func , . , , (, , ).
:
HoTT JetBrains Research.