Oh cette méthode de Newton

Beaucoup a été écrit sur les méthodes d'optimisation numérique. Cela est compréhensible, en particulier dans le contexte des succès récemment démontrés par les réseaux de neurones profonds. Et il est très gratifiant qu'au moins certains passionnés s'intéressent non seulement à la façon de bombarder leur réseau de neurones sur les frameworks qui ont gagné en popularité sur Internet, mais aussi à savoir comment et pourquoi tout cela fonctionne. Cependant, j'ai récemment dû noter que lorsque l'on pose des questions liées à la formation des réseaux de neurones (et pas seulement à la formation, et pas seulement aux réseaux), y compris sur Habré, un certain nombre de déclarations «bien connues» sont utilisées pour la transmission, dont la validité est pour le dire doucement, douteux. Parmi ces déclarations douteuses:

1. Les méthodes du deuxième ordre et plus ne fonctionnent pas bien dans les tâches de formation des réseaux de neurones. Parce que ça.
2. La méthode de Newton nécessite une définition positive de la matrice de Hesse (dérivées secondes) et ne fonctionne donc pas bien.
   
3. La méthode de Levenberg-Marquardt est un compromis entre la descente de gradient et la méthode de Newton et est généralement heuristique.
   

etc. Que de continuer cette liste, il vaut mieux se mettre aux affaires. Dans cet article, nous examinerons la deuxième déclaration, car je ne l'ai rencontré qu'au moins deux fois à Habré. Je n'aborderai la première question que dans la partie concernant la méthode de Newton, car elle est beaucoup plus étendue. Le troisième et le reste seront laissés jusqu'à des temps meilleurs.

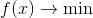
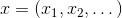
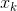
Le centre de notre attention sera la tâche de l'optimisation inconditionnelle où - un point d'espace vectoriel, ou simplement - un vecteur. Naturellement, cette tâche est plus facile à résoudre, plus nous en savons sur . Il est généralement supposé être différenciable en ce qui concerne chaque argument , et autant de fois que nécessaire pour nos actes sales. 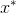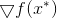Il est bien connu qu'une condition nécessaire pour cela à un moment donné le minimum est atteint, c'est l'égalité du gradient de la fonction à ce point zéro. De là, nous obtenons instantanément la méthode de minimisation suivante:

Résoudre l'équation .

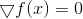
La tâche, pour le moins, n'est pas facile. Certainement pas plus facile que l'original. Cependant, à ce stade, nous pouvons immédiatement noter le lien entre le problème de minimisation et le problème de la résolution d'un système d'équations non linéaires. Cette connexion nous reviendra lors de l'examen de la méthode Levenberg-Marquardt (lorsque nous y arriverons). En attendant, rappelez-vous (ou découvrez) que l'une des méthodes les plus couramment utilisées pour résoudre des systèmes d'équations non linéaires est la méthode de Newton. Il consiste dans le fait que pour résoudre l'équation on part d'une approximation initiale construire une séquence

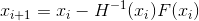
- La méthode explicite de Newton

ou

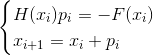
- La méthode implicite de Newton

où - matrice composée de dérivées partielles d'une fonction . Naturellement, dans le cas général, lorsque le système d'équations non linéaires nous est simplement donné en sensations, il faut quelque chose de la matrice nous n'avons pas droit. Dans le cas où l'équation est une condition minimale pour une fonction, nous pouvons affirmer que la matrice symétrique. Mais pas plus.

La méthode de Newton pour résoudre des systèmes d'équations non linéaires est très bien étudiée. Et voici la chose - pour sa convergence, le caractère définitif positif de la matrice n'est pas nécessaire . Oui, et ne peut être exigé - sinon il aurait été sans valeur. Au lieu de cela, il existe d'autres conditions qui assurent la convergence locale de cette méthode et que nous ne considérerons pas ici, en envoyant les personnes intéressées à la littérature spécialisée (ou dans le commentaire). Nous obtenons que la déclaration 2 est fausse.

Alors?

Oui et non. L'embuscade ici dans le mot est la convergence locale avant le mot. Cela signifie que l'approximation initiale doit être «assez proche» de la solution, sinon à chaque étape nous en serons de plus en plus éloignés. Que faire? Je n'entrerai pas dans les détails de la manière dont ce problème est résolu pour les systèmes d'équations non linéaires de forme générale. Revenons plutôt à notre tâche d'optimisation. La première erreur de l'énoncé 2 est en fait qu'en parlant généralement de la méthode de Newton dans les problèmes d'optimisation, cela signifie sa modification - la méthode de Newton amortie, dans laquelle la séquence d'approximations est construite selon la règle

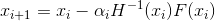
- La méthode amortie explicite de Newton

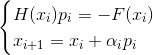
- La méthode amortie implicite de Newton

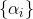
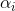
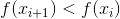
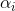
Voici la séquence est un paramètre de la méthode et sa construction est une tâche distincte. Dans les problèmes de minimisation, naturel lors du choix il faudra que, à chaque itération, la valeur de la fonction f diminue, c'est-à-dire . Une question logique se pose: existe-t-il un tel (positif) ? Et si la réponse à cette question est positive, alors appelé le sens de la descente. Ensuite, la question peut être posée de cette façon:
quand la direction générée par la méthode de Newton est-elle la direction de descente?
Et pour y répondre, vous devrez regarder le problème de la minimisation d'un autre côté.

Méthodes de descente

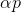
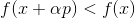
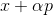
Pour le problème de minimisation, cette approche semble assez naturelle: à partir d'un point arbitraire, nous choisissons la direction p d'une certaine manière et faisons un pas dans cette direction . Si puis prenez comme nouveau point de départ et répétez la procédure. Si la direction est choisie arbitrairement, une telle méthode est parfois appelée méthode de marche aléatoire. Il est possible de prendre des vecteurs de base unitaire comme direction - c'est-à-dire de faire un pas dans une seule coordonnée, cette méthode est appelée méthode de descente de coordonnées. Inutile de dire qu'ils sont inefficaces? Pour que cette approche fonctionne bien, nous avons besoin de garanties supplémentaires. Pour ce faire, nous introduisons une fonction auxiliaire . 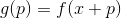Je pense qu'il est évident que la minimisation complètement équivalent à minimiser . Si différenciable alors peut être représenté comme



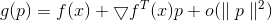
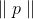
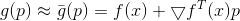
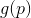
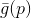
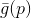
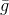
et si assez petit alors . Nous pouvons maintenant essayer de remplacer le problème de minimisation la tâche de minimiser son approximation (ou modèle ) . Soit dit en passant, toutes les méthodes basées sur l'utilisation du modèle appelé gradient. Mais le problème est, Est une fonction linéaire et, par conséquent, elle n'a pas de minimum. Pour résoudre ce problème, nous ajoutons une restriction sur la longueur de l'étape que nous voulons effectuer. Dans ce cas, il s'agit d'une exigence tout à fait naturelle - car notre modèle décrit plus ou moins correctement la fonction objectif uniquement dans un voisinage suffisamment petit. En conséquence, nous obtenons un problème supplémentaire d'optimisation conditionnelle:



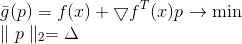
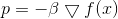
Cette tâche a une solution évidente: où - facteur garantissant le respect de la contrainte. Les itérations de la méthode de descente prennent alors la forme

,

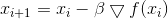
dans lequel nous apprenons la méthode bien connue de descente de gradient . Paramètre , qui est généralement appelée vitesse de descente, a maintenant acquis une signification compréhensible, et sa valeur est déterminée à partir de la condition que le nouveau point se trouve sur une sphère d'un rayon donné, circonscrite autour de l'ancien point.

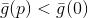
Sur la base des propriétés du modèle construit de la fonction objectif, nous pouvons affirmer qu'il existe une telle , même s'il est très petit, et si alors . Il est à noter que dans ce cas, la direction dans laquelle nous nous déplacerons ne dépend pas de la taille du rayon de cette sphère. Ensuite, nous pouvons choisir l'une des manières suivantes:

1. Sélectionnez selon une méthode la valeur .
2. Définissez la tâche de choisir la valeur appropriée , fournissant une diminution de la valeur de la fonction objectif.

La première approche est typique des méthodes de la région de confiance , la seconde conduit à la formulation du problème auxiliaire de la soi-disant recherche linéaire (LineSearch) . Dans ce cas particulier, les différences entre ces approches sont faibles et nous ne les considérerons pas. Faites plutôt attention aux points suivants:

pourquoi, en fait, recherchons-nous un décalage couché exactement sur la sphère?

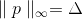
En fait, nous pourrions bien remplacer cette restriction par l'exigence, par exemple, que p appartienne à la surface du cube, c'est-à-dire, (dans ce cas, ce n'est pas trop raisonnable, mais pourquoi pas), ou une surface elliptique? Cela semble déjà tout à fait logique, si nous rappelons les problèmes qui se posent lors de la minimisation des fonctions de ravin. L'essence du problème est que le long de certaines lignes de coordonnées, la fonction change beaucoup plus rapidement que sur d'autres. Pour cette raison, nous obtenons que si l'incrément doit appartenir à la sphère, alors la quantité à laquelle la «descente» est prévue doit être très faible. Et cela conduit au fait que l'atteinte d'un minimum nécessitera un très grand nombre d'étapes. Mais si au lieu de cela nous prenons une ellipse appropriée comme voisinage, alors ce problème viendra par magie à néant.

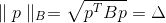
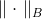
Par la condition d'appartenance des points de la surface elliptique, elle peut s'écrire où Est une matrice définie positive, également appelée métrique. Norm appelé la norme elliptique induite par la matrice . De quel type de matrice s'agit-il et où l'obtenir - nous y réfléchirons plus tard, et maintenant nous arrivons à une nouvelle tâche.



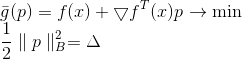
Le carré de la norme et le facteur 1/2 sont ici uniquement pour plus de commodité, afin de ne pas salir les racines. En appliquant la méthode du multiplicateur de Lagrange, on obtient le problème lié de l'optimisation inconditionnelle



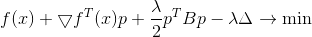
Une condition nécessaire pour un minimum car c'est

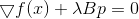
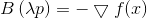
, ou d'où







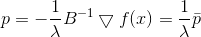
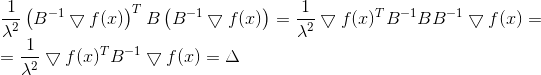
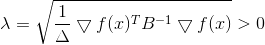
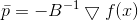
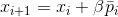
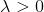
Encore une fois, nous voyons que la direction , dans lequel nous allons nous déplacer, ne dépend pas de la valeur - uniquement à partir de la matrice . Et encore une fois, nous pouvons soit ramasser qui est lourde de la nécessité de calculer et inversion matricielle explicite , ou résoudre le problème auxiliaire de trouver un biais approprié . Depuis , la solution à ce problème auxiliaire est garantie d'exister.

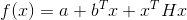
Alors, que devrait-il être pour la matrice B? Nous nous limitons aux idées spéculatives. Si la fonction objectif - quadratique, c'est-à-dire qu'il a la forme où positif défini, il est évident que le meilleur candidat pour le rôle de la matrice est jute , car dans ce cas, une itération de la méthode de descente que nous avons construite est requise. Si H n'est pas défini positif, alors il ne peut pas s'agir d'une métrique, et les itérations construites avec lui sont des itérations de la méthode de Newton amortie, mais ce ne sont pas des itérations de la méthode de descente. Enfin, nous pouvons donner une réponse rigoureuse à

Question: La matrice de Hesse dans la méthode de Newton doit-elle être définie positive?
Réponse: non, ce n'est requis ni dans la méthode standard ni dans la méthode de Newton amortie. Mais si cette condition est satisfaite, alors la méthode de Newton amortie est une méthode de descente et a la propriété d' une convergence globale , et pas seulement locale.

À titre d'illustration, voyons à quoi ressemblent les régions de confiance lors de la réduction de la fonction bien connue de Rosenbrock à l'aide de la descente en gradient et des méthodes de Newton, et comment la forme des régions affecte la convergence du processus.



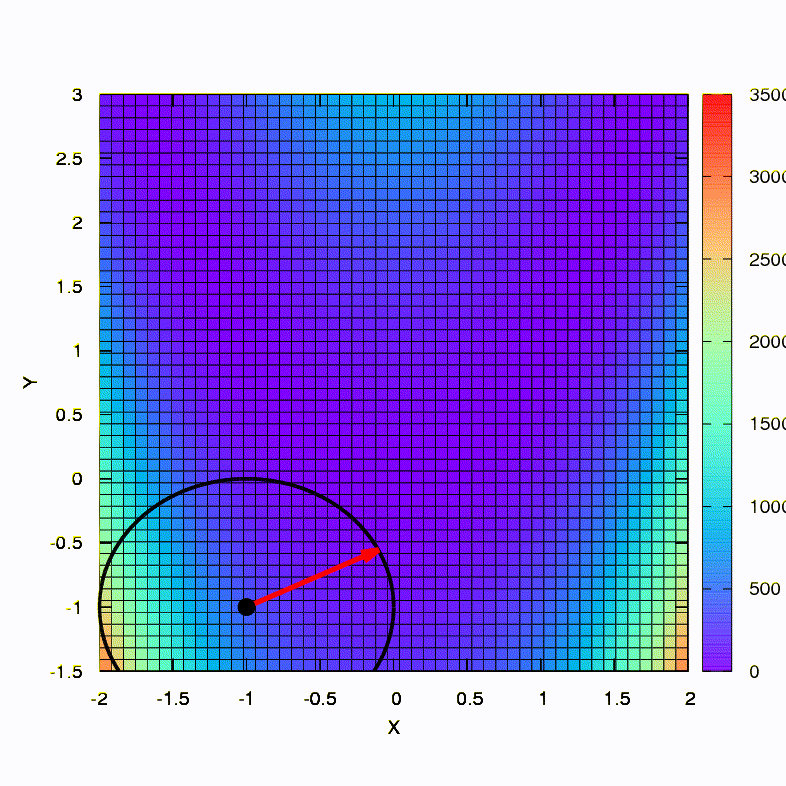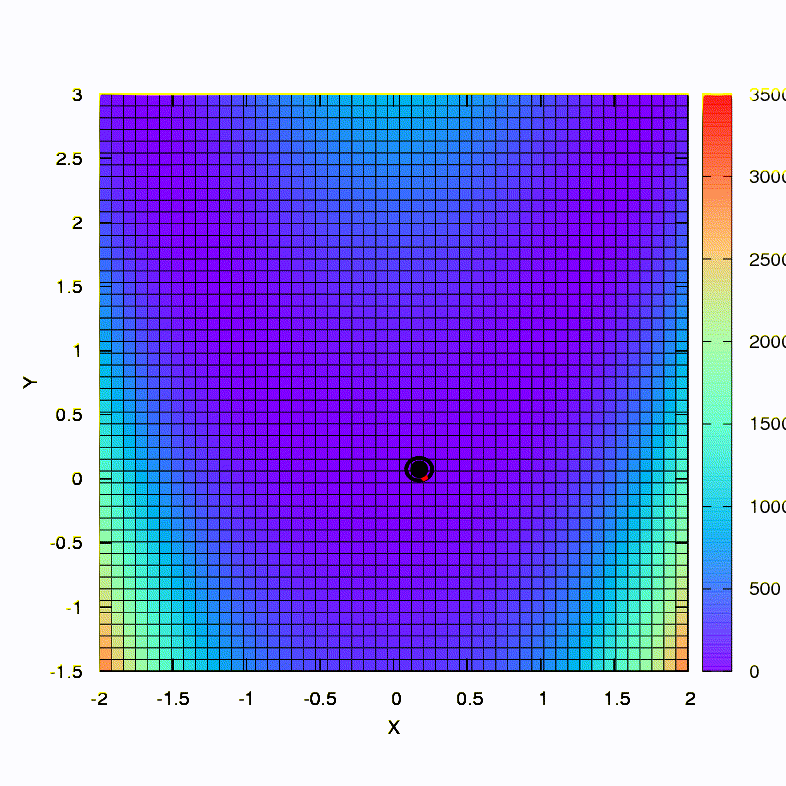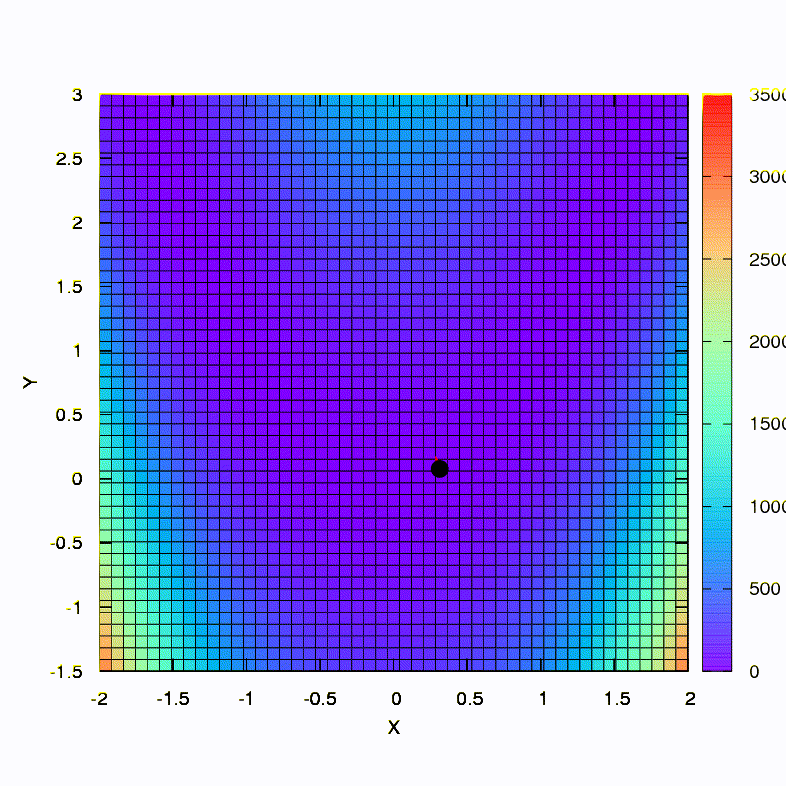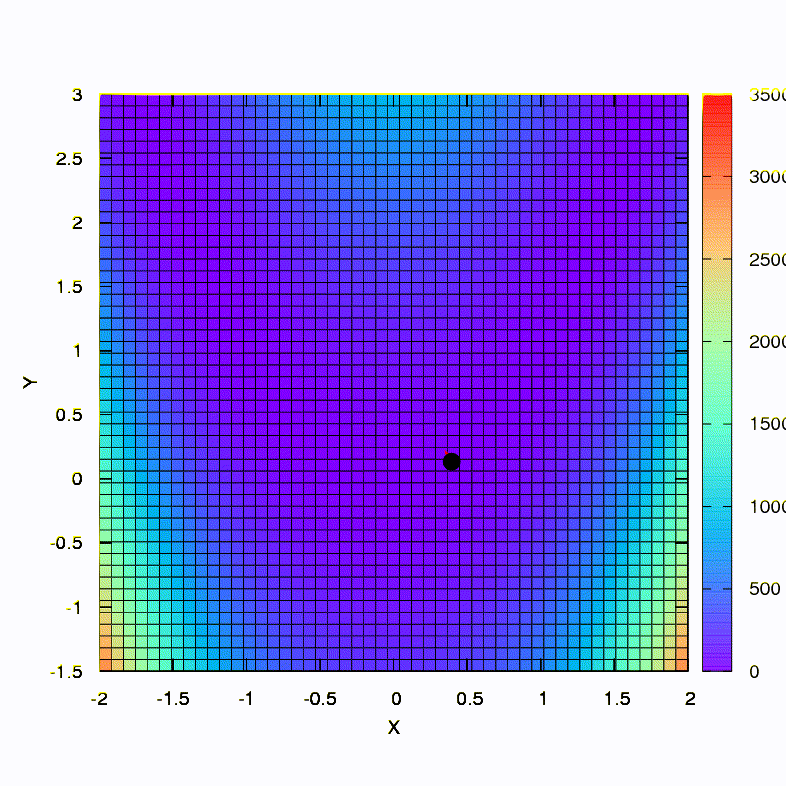
C'est ainsi que la méthode de descente se comporte avec une région de confiance sphérique, c'est aussi une descente en gradient. Tout est comme un manuel - nous sommes coincés dans un canyon.



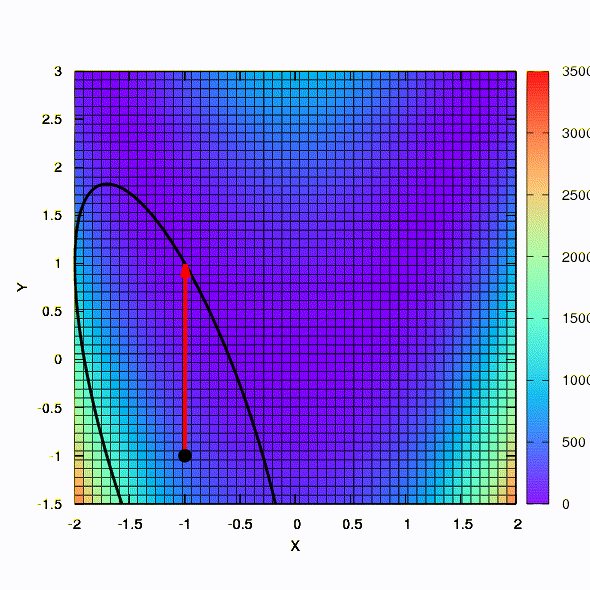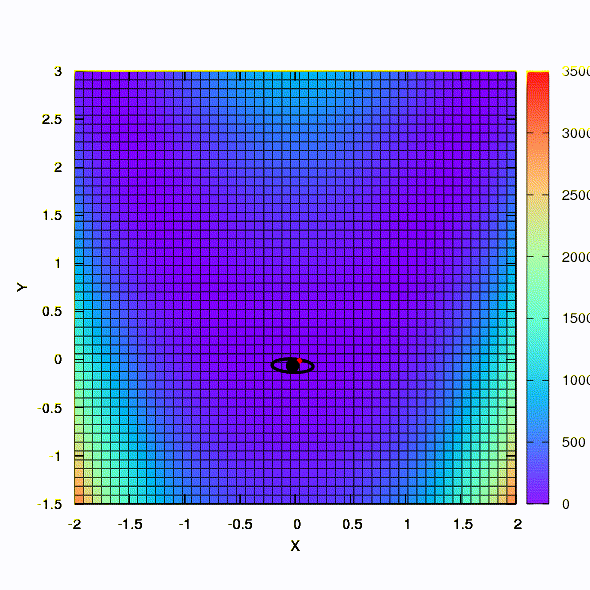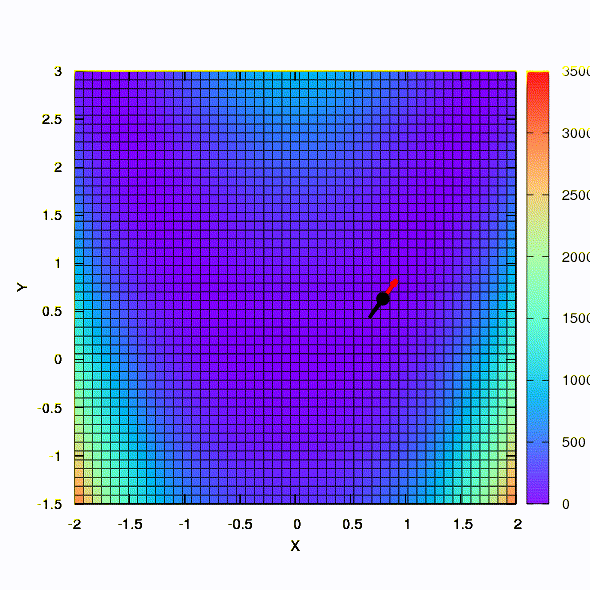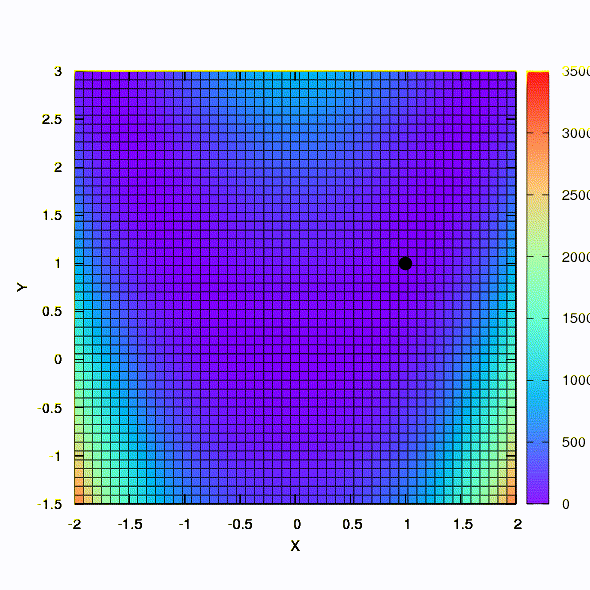
Et c'est ce que nous obtenons si la région de confiance a la forme d'une ellipse définie par la matrice de Hesse. Ce n'est rien de plus qu'une itération de la méthode Newton amortie.

Seule la question de savoir quoi faire si la matrice de Hesse n'est pas définie positive est restée non résolue. Il existe de nombreuses options. Le premier est de marquer. Vous avez peut-être de la chance et les itérations de Newton convergeront sans cette propriété. Ceci est tout à fait réel, en particulier aux étapes finales du processus de minimisation, lorsque vous êtes déjà suffisamment proche d'une solution. Dans ce cas, les itérations de la méthode standard de Newton peuvent être utilisées sans se soucier de la recherche d'un quartier admissible à la descente. 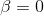Ou utilisez des itérations de la méthode Newton amortie dans le cas de c'est-à-dire que dans le cas où la direction obtenue n'est pas la direction de descente, changez-la, disons, en anti-gradient. Il suffit de ne pas vérifier explicitement si la Hesse est définie positive selon le critère Sylvestre , comme cela a été fait ici !!! . C'est inutile et inutile.
Des méthodes plus subtiles impliquent la construction d'une matrice, dans un sens proche de la matrice de Hesse, mais possédant la propriété d'être définitivement définitif, notamment en corrigeant les valeurs propres. Un autre sujet est les méthodes quasi-newtoniennes, ou méthodes métriques variables, qui garantissent le caractère définitif positif de la matrice B et ne nécessitent pas le calcul des dérivées secondes. En général, une discussion détaillée de ces questions dépasse largement le cadre de cet article.

Oui, et en passant, il résulte de ce qui a été dit que la méthode amortie de Newton avec une définition positive de la Hesse est une méthode de gradient . Ainsi que des méthodes quasi-newtoniennes. Et bien d'autres, basés sur un choix séparé de direction et de taille de pas. Il est donc incorrect de comparer la méthode de Newton à la terminologie du gradient.

Pour résumer

La méthode de Newton, dont on se souvient souvent lors de l'examen des méthodes de minimisation, n'est généralement pas la méthode de Newton dans son sens classique, mais la méthode de descente avec la métrique spécifiée par la Hesse de la fonction objectif. Et oui, il converge globalement si la Hesse est partout définie positive. Cela n'est possible que pour les fonctions convexes, qui sont beaucoup moins courantes dans la pratique que nous le souhaiterions, donc dans le cas général, sans les modifications appropriées, l'application de la méthode de Newton (nous ne nous détacherons pas du collectif et continuerons à l'appeler ainsi) ne garantit pas le résultat correct. L'apprentissage des réseaux de neurones, même peu profonds, conduit généralement à des problèmes d'optimisation non convexes avec de nombreux minima locaux. Et voici une nouvelle embuscade. La méthode de Newton converge généralement (si elle converge) rapidement. Je veux dire très vite. Et cela, curieusement, est mauvais, car nous arrivons à un minimum local en plusieurs itérations. Et cela pour les fonctions avec un terrain complexe peut être bien pire que le global. La descente en pente avec recherche linéaire converge beaucoup plus lentement, mais est plus susceptible de «sauter» les arêtes de la fonction objectif, ce qui est très important dans les premiers stades de la minimisation. Si vous avez déjà bien réduit la valeur de la fonction objectif et que la convergence de la descente du gradient a considérablement ralenti, un changement de métrique pourrait bien accélérer le processus, mais c'est pour les étapes finales.

Bien sûr, cet argument n'est pas universel, pas incontestable, et dans certains cas, même incorrect. Ainsi que l'affirmation que les méthodes de gradient fonctionnent mieux dans les problèmes d'apprentissage.