Fonctionnement de la méthode Levenberg-Marquardt

L'algorithme de Levenberg-Marquardt est simple. L'algorithme de Levenberg-Marquardt est efficace.

Et ils disent de lui qu'il est quelque part entre la descente en gradient et la méthode Newton, quoi que cela signifie. Eh bien, c'est en quelque sorte réglé avec la méthode de Newton et sa connexion avec la descente en gradient. Mais que signifient-ils lorsqu'ils prononcent cette phrase profonde? Essayons un petit peu.

Dans ses articles, le camarade Levenberg [K. Une méthode pour la résolution de certains problèmes dans les derniers carrés. Quart. Appl. Math. 1944. Vol. 2. P. 164-168.], Et après lui le citoyen Marquardt [Marquardt, Donald (1963). "Un algorithme pour l'estimation des moindres carrés des paramètres non linéaires." SIAM Journal on Applied Mathematics. 11 (2): 431–441.] Considéré comme le problème des moindres carrés, qui ressemble à ceci:

,

qui peut être écrit plus facilement sous forme vectorielle

.

Et vous pouvez encore plus facile en marquant complètement sur les moindres carrés. Cela n'affectera pas l'histoire.

Donc, le problème est considéré

.

Un tel problème se pose si souvent que l’importance de trouver une méthode efficace pour le résoudre ne peut guère être surestimée. Mais nous partirons d'un autre. Dans un article précédent, il a été montré que la méthode bien connue de descente de gradient, et pas seulement, peut être obtenue à partir des considérations suivantes. Disons que nous arrivons à un certain point dans lequel la fonction minimisée compte . 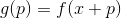Nous définissons une fonction auxiliaire à ce point , ainsi que certains de ses modèles . 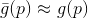Pour ce modèle, nous posons un problème auxiliaire



où - un certain ensemble prédéterminé de valeurs admissibles, choisi pour que le problème ait une solution simple et la fonction approximativement assez précisément sur . Ce schéma est appelé méthode de la région de confiance, et de nombreux sur laquelle la valeur de la fonction de modèle est minimisée - la région de confiance de cette fonction. Pour la descente en pente, nous avons pris , pour la méthode de Newton , et comme modèle pour la partie linéaire de l'expansion de Taylor .

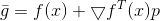
Voyons ce qui se passe si on complique le modèle en prenant

.

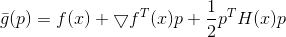
Nous minimisons cette fonction de modèle sur une région de confiance elliptique (multiplicateur ajouté pour faciliter le calcul). En appliquant la méthode du multiplicateur de Lagrange, on obtient le problème

,

dont la solution satisfait l'égalité



ou



Ici, contrairement à ce que nous avons vu précédemment lors de l'utilisation du modèle linéaire, la direction p ne dépend pas seulement de la métrique , mais aussi sur le choix de la taille de la région de confiance , ce qui signifie que la technique de recherche linéaire n'est pas applicable (du moins raisonnablement). Il s'avère également difficile de déterminer explicitement la valeur correspondant à . Cependant, il est évident qu'avec une augmentation longueur va diminuer. 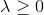Si, cependant, nous imposons toujours la condition , alors la longueur de pas ne sera plus que celle que donnerait la méthode de Newton (tout à la mode, sans modifications ni conditions).

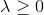
Nous pouvons donc plutôt pour une donnée chercher la bonne valeur , faites exactement le contraire: trouvez ceci dans lequel la condition . Il s'agit d'une sorte de remplacement de la recherche tardive dans ce cas. Marquardt a proposé la procédure simple suivante:

1. si pour une certaine valeur condition 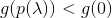fait puis répétez jusqu'à
2. si 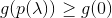alors accepte 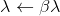et répéter.

Ici et Sont des constantes qui sont des paramètres de méthode. Multiplication par correspond à l'expansion de la région de confiance, et la multiplication par - son rétrécissement.

La technique spécifiée peut être appliquée à n'importe quelle fonction objective. Il est à noter qu'ici, le caractère définitif positif de la Hesse n'est plus requis, contrairement au cas considéré précédemment, lorsque la méthode de Newton était présentée comme un cas particulier de la méthode de descente séquentielle. Même sa non-dégénérescence n'est pas requise, ce qui dans certains cas est très important. Cependant, dans ce cas, le prix de la recherche de sens augmente, car chaque changement conduit à la nécessité de résoudre un système linéaire pour déterminer .

Voyons ce qui se passe si nous appliquons cette approche au problème des moindres carrés.

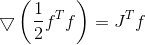
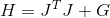
Fonction dégradé sa toile de jute où . Remplacez et obtenez le système suivant qui détermine la direction de la recherche

.

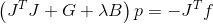
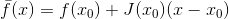
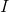
C'est tout à fait acceptable, mais le calcul des dérivées secondes d'une fonction vectorielle peut être assez coûteux. Marquardt a proposé d'utiliser la fonction elle-même pour contourner ce problème. , et son approximation linéaire à laquelle la matrice devient nul. Si maintenant prendre la matrice d'identité , nous obtenons alors la forme standard de la méthode de Levenberg-Marquardt pour résoudre le problème des moindres carrés:

.

Pour cette méthode de détermination de la direction de descente, Marquardt a prouvé le théorème qu'avec l'aspiration à l'infini a tendance à anti-gradient. Le lecteur intéressé peut trouver une preuve rigoureuse dans l'article de base, mais j'espère que cette affirmation elle-même est devenue assez évidente dans la logique de la méthode. Dans une certaine mesure, cela justifie la référence omniprésente au fait qu'avec une augmentation de lambda (que pour une raison quelconque j'appelle souvent le paramètre de régularisation), nous obtenons une descente de gradient. En fait, rien de tel - nous ne l'obtiendrions que dans la limite, dans celle-là même où la longueur de pas tend vers zéro. Il est beaucoup plus important qu'avec une valeur lambda suffisamment grande, la direction que nous obtenons soit la direction de descente , ce qui signifie que nous obtenons la convergence globale de la méthode . Et voici la deuxième partie de la déclaration que lorsque la lambda tend vers zéro, nous obtenons la méthode de Newton, c'est clairement vrai, mais seulement si nous acceptons à la place son approximation linéaire .

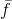
Il semblerait que tout. Nous minimisons la norme de la fonction vectorielle dans la métrique elliptique - nous utilisons le Levenberg-Marquardt. Nous avons affaire à une fonction de forme générale et avons la capacité de calculer la matrice des dérivées secondes - pour Wells, utilisez la méthode de région de confiance de région générale. Mais il y a des pervers ...

Parfois, la méthode de Levenberg-Marquardt pour minimiser la fonction ils appellent une expression comme celle-ci:

.

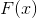
Tout semble être le même, mais ici - matrice du second! fonctions dérivées . Officiellement, cela a le droit d'exister, mais c'est une perversion. Et voici pourquoi. Le même Marquardt dans son article a proposé une méthode pour résoudre un système d'équations en minimisant la fonction la méthode décrite. Si comme prendre le gradient de la fonction objectif, alors on obtient vraiment l'expression réduite. Et la perversion est parce que

le problème de minimisation généré par le système d'équations non linéaires généré par le problème de minimisation est résolu .

Double coup. Une telle expression, au moins, n'est pas meilleure que la première équation d'une région de confiance sphérique, mais en général est bien pire à la fois du point de vue de la productivité (opérations de multiplication inutiles et dans les mises en œuvre normales - factorisation), et du point de vue de la stabilité de la méthode (la multiplication de la matrice en soi s'aggrave son conditionnement). On objecte parfois que garantie définie positivement, mais dans ce cas, cela n'a pas d'importance. Regardons la méthode de Levenberg-Marquardt du point de vue de la méthode de descente séquentielle. 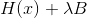Dans ce cas, il s'avère que nous voulons utiliser la matrice comme métrique , et pour qu'elle puisse agir en cette qualité, le sens devrait garantir sa certitude positive. Étant donné que valeur définie positive peut toujours être trouvé - et donc pas besoin d'exiger de une certitude positive n'est pas observée.

Comme matrice il n'est pas nécessaire d'en prendre une seule, mais pour un modèle quadratique de la fonction objectif, spécifier une région de confiance adéquate n'est plus aussi simple que pour un modèle linéaire. Si nous prenons la région elliptique induite par la Hesse, alors la méthode dégénère en méthode de Newton (enfin, presque)



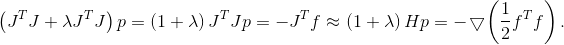
À moins, bien sûr, que la matrice de Hesse ne soit définie positive. Sinon, comme précédemment, vous pouvez utiliser la Hesse corrigée comme métrique, ou une matrice qui en quelque sorte est proche. Il est également recommandé d'utiliser une matrice comme métrique , qui, par construction, est garanti positif définitif. Malheureusement, je ne connais au moins aucune justification rigoureuse de ce choix, mais il est mentionné assez souvent comme une recommandation empirique.

À titre d'illustration, voyons comment la méthode se comporte sur la même fonction de Rosenbrock, et nous la considérerons sous deux formes - comme une simple fonction écrite sous la forme

,

et comme un problème des moindres carrés




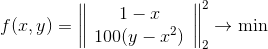
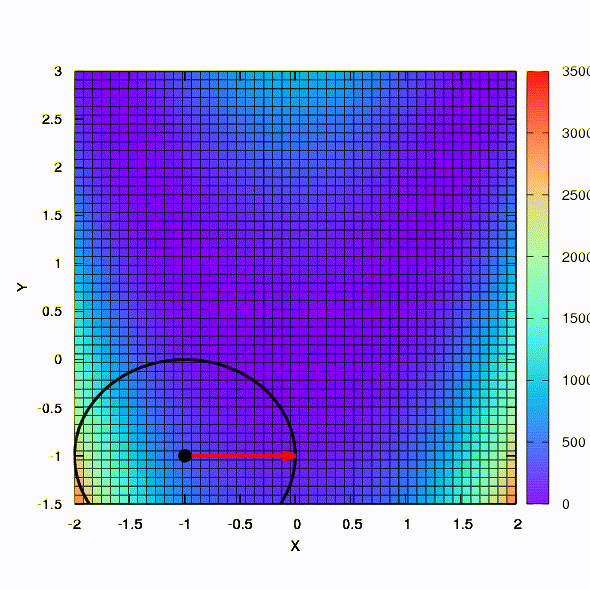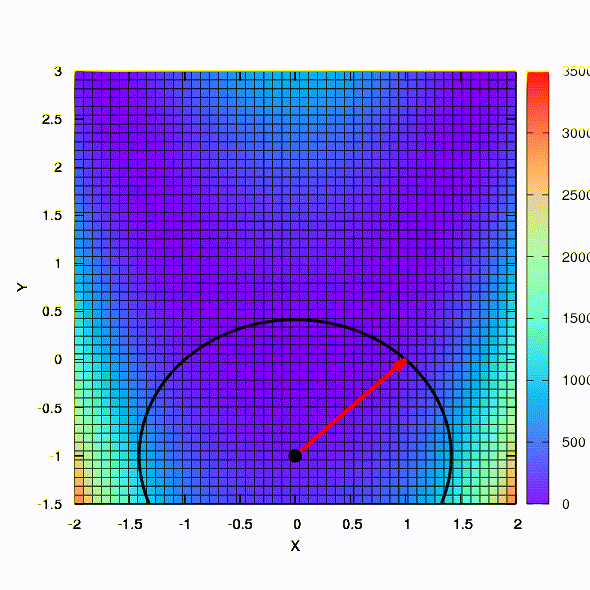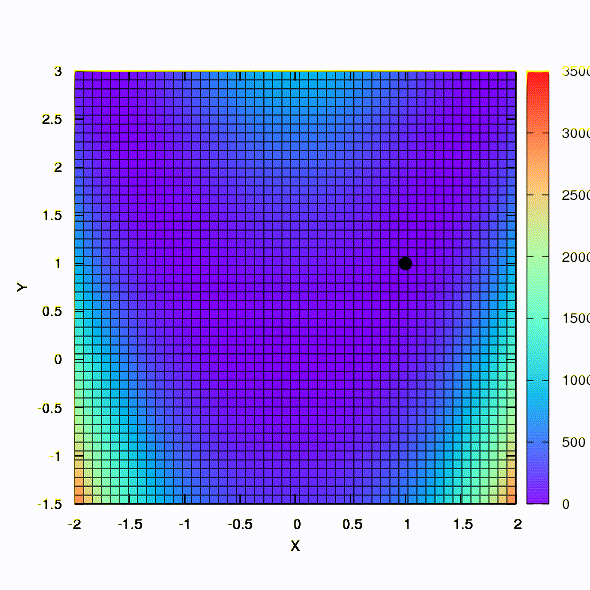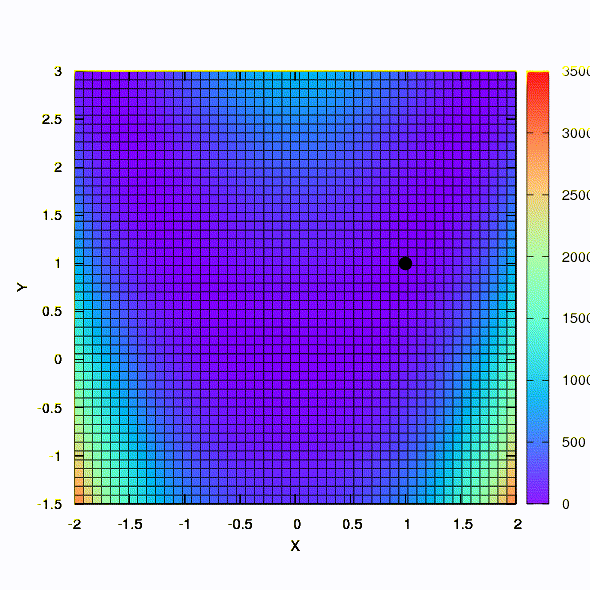
Voici comment se comporte une méthode avec une région de confiance sphérique.

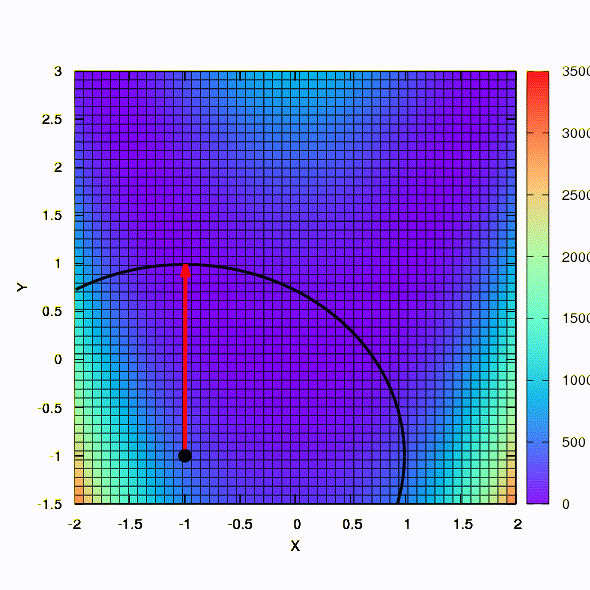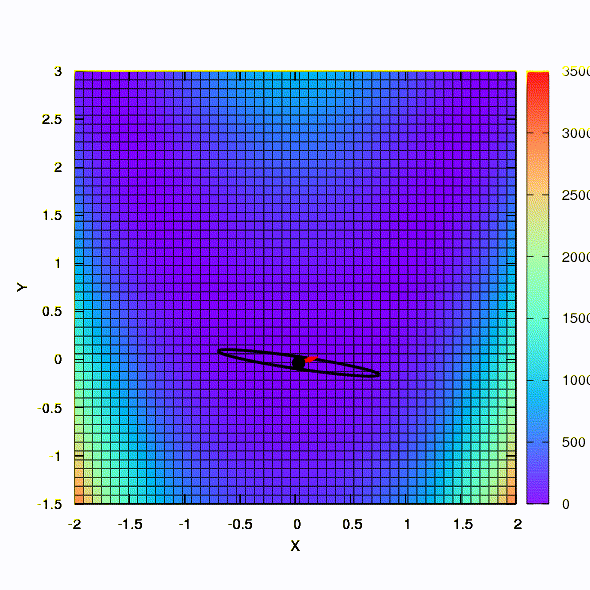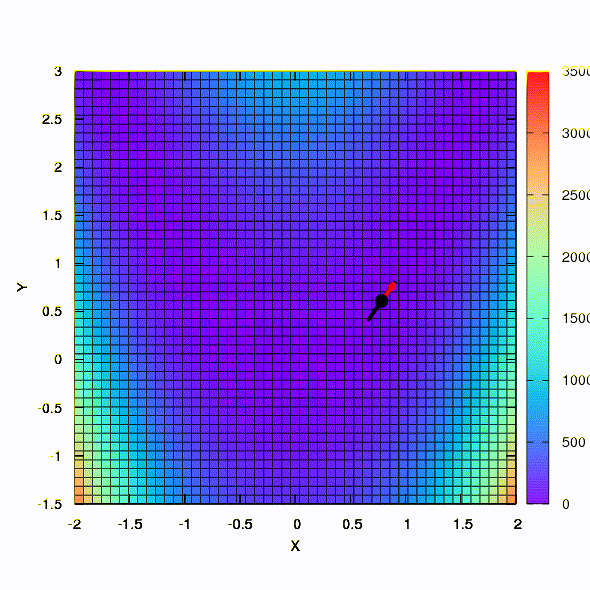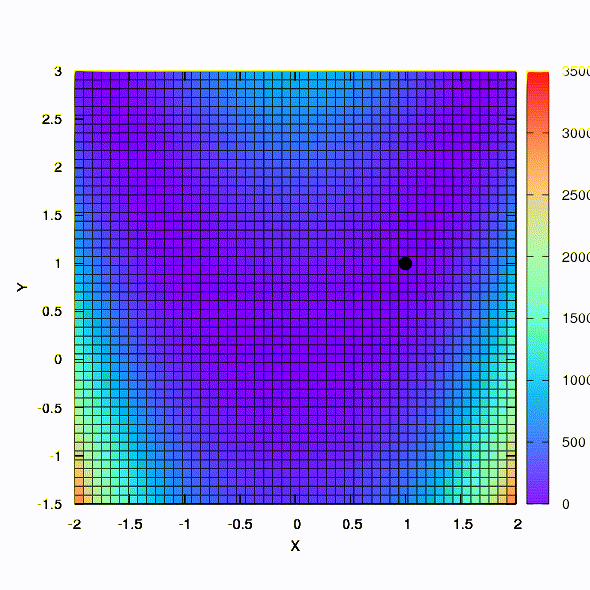
Ainsi, la même méthode se comporte si la forme de la région de confiance est donnée par une matrice construite selon la règle de Davidon-Fletcher-Powell. Il y a un effet sur la convergence, mais beaucoup plus modeste que dans le cas similaire lors de l'utilisation du modèle linéaire de la fonction objectif.

Et c'est le comportement de la méthode appliquée au problème des moindres carrés. Il converge en 5 itérations. Je vous en prie, ne tirez pas de cette conclusion que la deuxième formulation pour des fonctions de ce genre est toujours meilleure que la première . Ce n'est pas le cas, c'est juste arrivé dans ce cas particulier.

Conclusion

La méthode de Levenberg-Marquardt est, à ma connaissance, la première méthode basée sur l'idée d'une région de confiance. Il s'est très bien montré en pratique lors de la résolution du problème des moindres carrés. La méthode converge dans la plupart des cas (vue par moi) assez rapidement (j'ai dit si c'était bon ou mauvais dans un article précédent). Cependant, tout en minimisant les fonctions générales, ce n'est guère la meilleure option pour choisir une sphère comme région de confiance. De plus, un inconvénient important de la méthode (dans sa formulation de base, qui a été décrite ici) est que la taille de la région de confiance est définie implicitement. L'inconvénient est que connaître le sens nous pouvons bien sûr compter au point actuel juste calculer la longueur de foulée . Cependant, lorsque nous passons à un nouveau point, la même valeur une valeur complètement différente de la région de confiance correspondra déjà. Ainsi, nous perdons la capacité de déterminer la taille «caractéristique de la tâche» de la région de confiance et sommes obligés de déterminer sa taille d'une nouvelle manière à chaque nouveau point. Cela peut être significatif lorsqu'un nombre d'itérations suffisamment important est requis pour la convergence et que le calcul de la valeur d'une fonction est coûteux. Des problèmes similaires sont résolus dans des méthodes plus avancées basées sur l'idée d'une région de confiance.

Mais c'est une histoire complètement différente.

Addition

Grâce aux précieux commentaires de Dark_Daiver, j'ai décidé que ce qui précède devrait être complété par la remarque suivante. Bien sûr, on peut arriver à la méthode Levenberg-Marquardt d'une manière différente, purement empirique. À savoir, revenons au schéma de la méthode de descente séquentielle décrit dans l'article précédent et posons-nous à nouveau la question de construire une métrique adéquate pour le modèle linéaire de la fonction objectif.
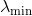
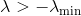
Supposons que la matrice de Hesse au point actuel dans l'espace de recherche ne soit pas définie positive et ne puisse pas servir de métrique (de plus, pour vérifier si c'est le cas, nous n'avons ni la capacité ni le désir). Désigner par sa plus petite valeur propre. Ensuite, nous pouvons corriger la Hesse en déplaçant simplement toutes ses valeurs propres par . Pour ce faire, il suffit d'ajouter la matrice à la toile de jute . 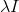L'équation déterminant le sens de la descente prendra alors la forme



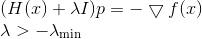
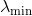
Si nous avons un bon score inférieur pour , alors nous pouvons faire tout ce qui a été fait dans les méthodes de descente séquentielle. Cependant, si nous ne disposons pas d'une telle estimation, alors en tenant compte qu'avec une augmentation la longueur p diminuera, on peut dire avec certitude qu'il y a un tel suffisamment grand qu'en même temps positif défini et .

Pourquoi je considère qu'une telle conclusion de la méthode n'est pas trop réussie. Premièrement, il n'est pas du tout évident que la métrique ainsi construite convient à une utilisation pratique. Il utilise, bien sûr, des informations sur les dérivées secondes, mais il ne s'ensuit pas de quelque part que le décalage des valeurs propres d'une valeur donnée ne le rendra pas inutilisable. Comme l'a noté le collègue dans les commentaires, il semble évident que l'ajout d'une matrice d'identité à l'échelle à la matrice de Hesse conduit au fait que la région de confiance elliptique aura tendance à être sphérique et là encore (comme il semble) les problèmes de coincement dans le canyon et d'autres délices de descente de gradient et de proches pour lui les méthodes. Mais en pratique, cela ne se produit pas. En tout cas, je n'ai jamais pu observer d'exemples illustrant un tel comportement. Dans ce cas, la question se pose: mais, en fait, pourquoi ?

Mais une telle question ne se pose pas si nous considérons cette méthode non pas comme un cas particulier de méthodes de descente, mais comme une méthode de région de confiance avec un modèle quadratique de la fonction objectif, car la réponse est évidente: lorsque le lambda augmente, nous compressons simplement la sphère - la région de confiance pour notre modèle. Les informations sur la courbure ne vont nulle part et ne sont emportées par rien - il suffit de choisir la taille de la région dans laquelle le modèle quadratique décrit correctement la fonction objectif. Il en résulte qu'il ne vaut guère la peine d'attendre un effet significatif d'un changement de métrique, c'est-à-dire la forme de la région de confiance, puisque toutes les informations dont nous disposons sur la fonction objectif sont déjà prises en compte dans son modèle.

Et deuxièmement, lors de l'examen d'une méthode, il est important de comprendre l'idée principale qui a conduit Marquardt à cette méthode, à savoir l'idée d'une région de confiance. En effet, en dernière analyse, seule la compréhension des tenants et aboutissants de la méthode numérique nous permettra de comprendre pourquoi elle fonctionne et, plus important encore, pourquoi elle peut ne pas fonctionner.