RESHI.RU - un robot résout et explique les problèmes de texte scolaire en mathématiques

Présentation

Lorsque j'ai expliqué à mon enfant en 4e année comment résoudre un problème de texte en mathématiques, j'ai soudain compris deux choses. Tout d'abord, le processus d'explication de la décision peut être automatisé. Et deuxièmement, pour la plupart des problèmes informatiques scolaires, une méthode universelle est appropriée grâce à un système d'équations qui, pour une raison quelconque, n'a pas encore été étudié dans les classes inférieures de l'école. De plus, la maîtrise de cette méthode est tout à fait à la portée du lycéen et lui permettra de faire face à des tâches qui lui étaient auparavant inaccessibles. Le résultat de cette compréhension a été le site Web RESHI.RU avec un robot expliquant les tâches.

La différence avec de nombreux sites avec des devoirs prêts à l'emploi est que le problème peut être résolu théoriquement par n'importe qui, et non prédéterminé. Mais seulement théoriquement, car dans la pratique, le robot ne comprend que les types de tâches pour lesquelles une implémentation logicielle a été effectuée. Sur les tâches des manuels pour la 4e année, le robot montre 65% des bonnes solutions (et s'il ne peut pas ou doute, puis en avertit honnêtement), pour la 3e année - environ 80%.
Le problème à résoudre doit être formulé avec un texte sans erreur, ne pas avoir d'informations graphiques dans la condition (images, diagrammes) et être informatique, c'est-à-dire que la réponse doit être une ou plusieurs quantités. Les valeurs dans l'état du problème peuvent être des nombres ou des variables.

Le robot essaie de composer un système d'équations simples pour le problème et de le résoudre. Pour certains types de tâches, le robot peut résoudre de manière scolaire, ce qui est proposé en tant que tâche supplémentaire.

Néanmoins, l'objectif principal de RESHI.RU n'est pas de résoudre des problèmes spécifiques, mais d'expliquer par des exemples la méthode universelle de résolution à travers un système d'équations simples.

Exemple de tâche

Prenons un exemple de robot résolvant le problème suivant sur le site Web RESHI.RU .

Deux bus ont quitté le village et la ville l'un vers l'autre. Un bus a parcouru 100 km jusqu'à la réunion à une vitesse de 25 km / h. Combien de kilomètres avant la rencontre le deuxième bus a parcouru si sa vitesse est de 50 km / h.

Le robot s'est rendu compte que c'était une tâche pour le mouvement de deux objets et il sait comment les résoudre. Reste
sélectionner correctement toutes les quantités, comprendre leurs types et corréler avec ces deux objets.
À titre d'explication, le robot affiche une séquence de sections, chacune décrivant l'un ou l'autre aspect, plus près de recevoir une réponse. Voici des captures d'écran de ces sections.









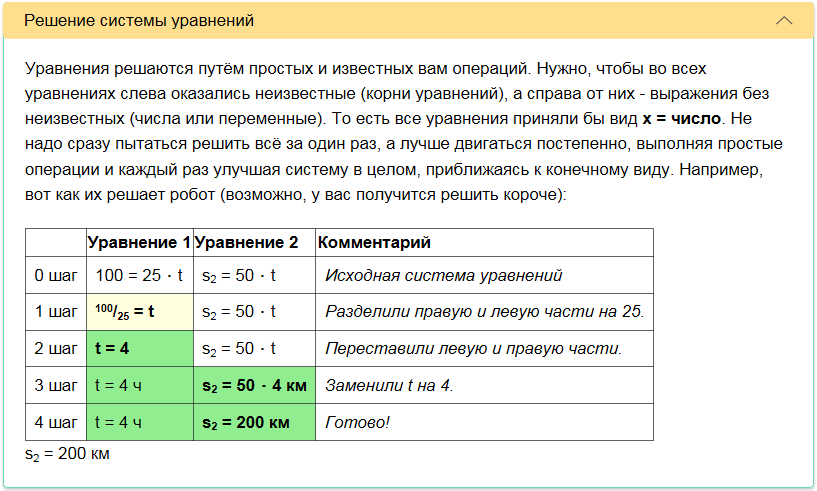
Le robot a également réalisé qu'en plus de la méthode universelle, il existe une méthode de solution scolaire, plus courte et plus simple.



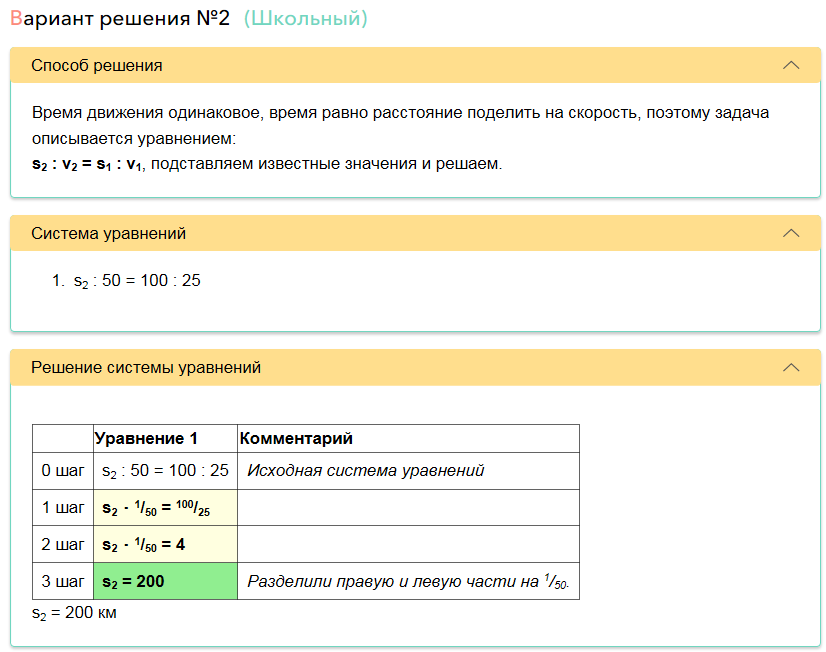
Tout cela avec le schéma est généré automatiquement pour chaque problème résolu et non défini initialement.

La façon universelle de résoudre

La plupart des problèmes de texte scolaire peuvent être résolus par la méthode universelle - grâce à un système d'équations simples. Si l'élève maîtrise cette méthode, il sera en principe en mesure de résoudre tout problème mathématique scolaire typique donné par le texte.

En 1re année, les écoliers apprennent à résoudre des problèmes simples décrits par une seule équation a = b + c ou a = b - c. Et en 3e année, après avoir maîtrisé les opérations de multiplication avec division, des problèmes simples apparaissent sur a = b ⋅ s ou a = b / c. Les problèmes composés sont des problèmes qui ne sont pas simples, c'est-à-dire qui ne sont pas décrits par une seule équation à trois quantités. Ici, l'étudiant est invité à être intelligent pour faire une équation complexe ou réduire le problème à un certain nombre de problèmes plus simples qui sont résolus les uns après les autres. Les tâches composites et soustractives composites sont activement proposées à partir de la 2e année, et à partir de la 3e année, la complexité augmente encore plus avec l'avènement de nouvelles opérations.

Mais il existe une autre façon de résoudre des problèmes composites, et elle consiste à compiler quelques équations simples (un système d'équations), puis à la résoudre dans son intégralité. En effet, si un élève peut résoudre des problèmes simples (c'est-à-dire composer correctement une équation simple en fonction du texte de la condition), alors pour un problème composite, il peut, en principe, composer sa propre équation simple pour chaque condition individuelle. Pour ce faire, toutes les quantités survenues doivent être désignées par leurs symboles (par exemple, x, y, z, ...), et les x = y + z, etc. correspondants doivent être formés pour elles. Remplacez ensuite des nombres spécifiques dans l'équation. Et puis résoudre ce système en déterminant séquentiellement des valeurs inconnues.

Cette méthode peut s'avérer plus longue à résoudre une tâche spécifique, car certains «faits saillants» simplifient généralement le travail. Mais il ne peut pas toujours être trouvé, car c'est une sorte d'art. Une méthode universelle n'exige pas cela, étant une technologie telle que "faites-le une fois, puis faites-en deux, et voici la réponse."

Le robot l'utilise de manière universelle et essaie d'expliquer le plus en détail possible sur une tâche spécifique comment il obtient une solution. Il est supposé que l'élève passera un certain temps à comprendre comment le robot le fait afin de répéter des actions similaires dans d'autres tâches à l'avenir. Cependant, le robot propose également une solution scolaire si le robot est formé pour cela pour ce type de tâche ( maintenant pas pour tous les types, mais apprend progressivement ).

Il est utile ou non pour les étudiants - un point discutable. D'une part, cela peut augmenter le pourcentage de tâches résolues par les étudiants. D'un autre côté, chez certains étudiants, une telle technologie peut supprimer les pousses délicates du savoir mathématique. Je propose d'envoyer à l'auteur ou d'écrire mes considérations et préoccupations raisonnables ici.

Classificateur de tâche

Selon un système d'équations simples, les problèmes peuvent être classés automatiquement. Cela peut être utile, par exemple, afin d'offrir à l'élève de résoudre un problème similaire pour consolider la compétence. De plus, le robot peut comprendre à quelle classe la tâche appartient, car même dans les manuels de 4e année il y a des problèmes de niveau de 1ère classe!

Actuellement, le site a téléchargé plus de 4000 tâches à partir de vrais manuels, et vous pouvez voir ce classificateur automatique pour ces tâches.

Implémentation du robot

Bien sûr, une question raisonnable se pose - comment fonctionne ce robot? Je dois dire que c'est une mise en œuvre très complexe . Je traite des textes en langage naturel depuis environ 10 ans, et c'est la tâche la plus difficile que j'ai rencontrée dans ce domaine. La difficulté réside dans le fait que vous devez sélectionner correctement les quantités numériques, comprendre leur type et se rapporter aux objets. Toute inexactitude dans au moins un aspect conduit à un résultat incorrect.
Je vais énumérer seulement certains des problèmes auxquels j'ai dû faire face.

• Pseudo-quantités qui ne sont pas pertinentes pour le problème (il y avait 2 roses en fleurs sur le buisson. Après 3 jours , 4 autres roses ont fleuri. Combien de roses sont sur le buisson?);
• Valeurs implicites données par différentes combinaisons du type "même", "moitié de" et ainsi de suite;
• Synonymie, lorsque le même objet est indiqué par différentes combinaisons (camion = camion);
• Difficulté à identifier les objets (les bateaux à moteur naviguaient de deux marinas l'une vers l'autre ... - on ne sait pas qui sont les objets ici, les marinas ou les bateaux à moteur?);
• Anaphora (pronom il, elle, elle) ne se réfère pas toujours uniquement à un objet;
• La nécessité de diviser la tâche en sous-tâches lorsque la condition de base est une, mais les conditions supplémentaires ou ce qui doit être trouvé sont variées;
• Une condition implicite qui change radicalement le sens de la tâche (La couverture de table a 3 angles. Un coin a été coupé. Combien de coins la couverture de table avait-elle?);

Mais c'est ce qui se trouve à la surface. Au niveau algorithmique, ces problèmes sont beaucoup plus importants.
L'idée principale de l'algorithme est que des gestionnaires de tâches spécifiques qui comprennent leurs types sont implémentés. La tâche est exécutée par tous les gestionnaires, et dont l'un reconnaît son type, ce qui résout le problème. Chaque gestionnaire résout un éventail assez large de tâches de son type.

Maintenant, ces types sont:

• Tâches pour le mouvement d'un ou plusieurs objets;
• Tâches sur des rectangles et des carrés (un ou plusieurs), des zones, des périmètres, se remplissant les uns les autres;
• Tâches pour des quantités homogènes (lorsque toutes les quantités sont réduites à une dimension et que la tâche elle-même est un système d'équations linéaires);
• Tâches pour les quantités à deux genres (lorsque la multiplication est présente dans le système d'équations);
• Décrire explicitement l'équation (par exemple, le quotient des nombres 2082 et 6 est égal à la somme du nombre voulu et du nombre 48);
• Tâches pour l'heure de la journée;
• Tâches en moyenne, transformation des dimensions et autres bagatelles;

Lorsque le robot a compris la tâche, c'est-à-dire qu'il l'a attribuée à l'un des types pris en charge, après avoir correctement défini les valeurs et compris ce qui doit être calculé, il peut générer sa compréhension avec son propre langage. Soit dit en passant, sur le site, cette compréhension est affichée à droite du texte des tâches pour les manuels. Nous donnons des exemples sur le site.

Condition : le quotient des nombres 2082 et 6 est égal à la somme du nombre voulu et du nombre 48.
Comprendre : trouver la racine de l'équation: 2082: 6 = x + 48.

Condition : Le jeu pour enfants a commencé à 11 heures et s'est terminé à 12 h 35 min. Combien de temps a duré cette représentation?
Comprendre : Il y a un intervalle de temps. Le début de l'intervalle est de 11 heures et la fin de l'intervalle est de 12 heures 35 minutes. Quelle est la durée de l'intervalle?

Condition : Ane a 12 ans. Elle est 3 fois plus âgée que son frère. Quel âge a Anya plus âgée que son frère?
Compréhension : Il y a 2 valeurs numériques: l'âge d'Ani et l'âge du frère. L'âge d'Ani est de 12 ans, il est 3 fois plus que l'âge de son frère. Combien a l'âge d'Ani plus que celui de son frère?

Condition : Un tourneur fait 8 pièces toutes les heures, et un autre - 7 pièces. Combien d'heures produiront-ils 90 pièces ensemble si leur production par heure ne change pas?
Comprendre : Il y a 2 objets: Turner n ° 1 et Turner n ° 2. Le nombre de pièces en heures de tourneur n ° 1: 8 parties. Le nombre de pièces en heures de tourneur n ° 2: 7 pièces. Le nombre total de pièces ensemble: 90 pièces. Tous les objets ont la même heure. Que signifie le temps en heures?

Condition : Deux camarades, Misha et Kolya, sont sortis de deux villages en même temps l'un vers l'autre. Misha marcha à une vitesse de 3 km / h et Kolya à 5 km / h. En même temps que Misha, un chien a couru vers Kolya. Elle a couru à une vitesse de 8 km / h. Quand elle a atteint Kolya, elle s'est retournée vers Misha et a couru entre les gars jusqu'à ce qu'ils se rencontrent. Combien de kilomètres le chien a-t-il parcouru si la distance entre les villages est de 16 km?
Comprendre : Deux objets (Misha et Kolya) ont simultanément commencé à se rapprocher à une distance de 16 km. Entre eux, le troisième objet (chien) se déplace d'avant en arrière à une vitesse de 8 km / h. Le premier objet (Misha) s'est déplacé à une vitesse de 3 km / h. Le deuxième objet (roue) s'est déplacé à une vitesse de 5 km / h. Quel chemin en km le 3e objet a-t-il franchi?

Condition : Dans la pièce, dont la longueur est de 8 m, et la largeur est inférieure de 2 m à la longueur, le sol doit être peint. De combien de peinture aurez-vous besoin si vous dépensez 150 g par 1 m2?
Comprendre : Un rectangle de 8 m de long et 2 m de moins que la longueur. La zone est remplie d'éléments de 150 g par unité de surface. Combien d'éléments sont sur toute la zone?

Et ensuite?

Les orientations de développement suivantes sont prévues:

• Augmentez le pourcentage de tâches. Maintenant, pour les tâches de la 4e classe, le robot affiche 65% des solutions correctes, pour la 3e classe - environ 80%, pour 1 et 2 - le pourcentage est encore plus élevé;
• Organiser la promotion du site Web;
• Présenter les tâches de tous les manuels populaires en mathématiques, y compris pour les pays de la CEI (en russe);
• Soutenir d'autres langues du groupe slave;
• Allez en 5e année et au-delà;
• Pensez aux problèmes de texte en physique;

La mise en œuvre de ces zones dépendra de la pertinence réelle du site.