L'article discutera de l'expérience de développement d'un programme pour créer un portefeuille obligataire efficace en termes de minimisation de sa durée . Je ne serai peut-être pas original et pour tous ceux qui investissent dans des obligations, les problèmes de détermination des pondérations optimales sont résolus depuis longtemps, mais j'espère néanmoins que l'approche décrite et le code de programme fourni seront utiles à quelqu'un.

L'article, en raison de la présence d'une petite quantité de mathématiques, peut sembler compliqué à quelqu'un. Mais si vous avez déjà décidé de commencer à investir, vous devez vous préparer au fait que les mathématiques se trouvent souvent dans la réalité financière et sont encore plus compliquées.

Le code source du programme et un exemple de portfolio pour l'optimisation sont disponibles sur GitHub.

MISE À JOUR: Comme promis, a fait un service Web simple qui rend le programme disponible pour tout le monde sans copier ni compiler de code.
le lien
Mode d'emploi au même endroit.
Si quelque chose ne fonctionne pas ou si vous devez réparer quelque chose - écrivez dans les commentaires.

Nous avons donc pour tâche de constituer un portefeuille d'obligations efficace.

Partie 1. Détermination de la durée du portefeuille

Du point de vue de la minimisation des risques non systémiques (pour lesquels le portefeuille est diversifié), le choix des titres a été effectué en considérant les paramètres d'une émission particulière, l'émetteur (sinon limité à l' OFZ ), le comportement papier, etc. (les approches d'une telle analyse sont assez individuelles pour chaque investisseur et ne sont pas prises en compte dans cet article).

Après avoir sélectionné plusieurs titres les plus préférables pour l'investissement, une question naturelle se pose: combien d'obligations de chaque émission devez-vous acheter? C'est la tâche d'optimiser le portefeuille afin que les risques du portefeuille soient minimes.

Il est naturel de considérer la durée comme un paramètre optimisé. Ainsi, la tâche consiste à déterminer le poids des titres en portefeuille, de telle sorte que la durée du portefeuille soit minimale pour un certain rendement fixe du portefeuille. Ici, vous devez faire quelques réservations:

1. La durée du portefeuille obligataire est déterminée par ses titres constitutifs. Ces durées sont connues (elles sont du domaine public). La durée du portefeuille n'est pas égale à la durée maximale des titres qui y sont inclus (il y a une telle erreur). La relation entre les durées de titres individuels et la durée de l'ensemble du portefeuille n'est pas linéaire, c'est-à-dire n'est pas égal à la durée moyenne pondérée de ses obligations constitutives (pour le vérifier, il suffit de considérer la formule de duration (voir (1) ci-dessous) et d'essayer de calculer la durée moyenne pondérée d'un portefeuille conditionnel composé, par exemple, de deux papiers. Substitution de la formule de duration dans une telle expression de chaque papier, à la sortie, nous obtenons non pas une formule pour la durée du portefeuille, mais une sorte de "non-sens", avec deux taux d'actualisation et des flux de trésorerie incohérents comme pondérations).
2. Contrairement à la duration, le rendement du portefeuille dépend linéairement des rendements des instruments qui y sont inclus. C'est-à-dire en plaçant de l'argent dans plusieurs instruments à revenu fixe, nous obtiendrons un rendement directement proportionnel au volume des investissements dans chaque instrument (et cela fonctionne pour un taux complexe, et pas seulement pour un simple). Assurez-vous que c'est encore plus facile.
3. Le rendement à l'échéance ( YTM ) est utilisé comme taux de rendement des obligations. Il est généralement utilisé pour calculer la durée. Cependant, le rendement à l'échéance de l'ensemble du portefeuille ici est plutôt arbitraire, car l'échéance de tous les titres est différente. Lors de la constitution d'un portefeuille, cette caractéristique doit être prise en compte dans le sens où le portefeuille doit être revu, tout comme les outils dont il est composé, sortent de la circulation.

Ainsi, la première tâche consiste à calculer correctement la durée du portefeuille lui-même. La manière immédiate de le faire est de: déterminer tous les paiements pour le portefeuille, calculer le rendement à l'échéance, actualiser les paiements, multiplier les valeurs reçues par les termes de ces paiements et additionner. Pour ce faire, vous devez combiner les calendriers de paiement de tous les instruments en un seul calendrier de paiement pour l'ensemble du portefeuille, composer une expression pour calculer le rendement à l'échéance, le calculer, l'escompter pour chaque paiement, multiplier par sa date d'échéance, ajouter ... En général, un cauchemar. Faire cela même pour deux articles est une tâche très laborieuse, sans parler de recalculer régulièrement le portefeuille à l'avenir. Cette façon ne nous convient pas.

Par conséquent, il est nécessaire de rechercher une opportunité pour déterminer la durée du portefeuille d'une manière différente et plus rapide. Une option acceptable serait celle qui vous permet de déterminer la durée du portefeuille en fonction des durées connues des instruments. Des études sur la formule de durée ont montré qu'il existe un tel chemin et ici je voudrais le donner en détail (si quelqu'un n'est pas intéressé par les détails mathématiques des calculs, vous pouvez sauter en toute sécurité quelques paragraphes avec les formules et aller directement à l'exemple).

La durée d'un instrument de dette est définie comme suit:

$$$$ afficher $$ \ commencer {équation} D = \ frac {\ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~~~ (1) \ fin {équation} $$ afficher $$

où:

• t _i est le moment de l'heure du i-ème paiement;
• $$$ inline $ \ begin {equation} PV_i = \ frac {CF_i} {(1 + r) ^ {t_i}} \ end {equation} $ inline $ - i-ème paiement à prix réduit;
• CF _i - i-ème paiement;
• r est le taux d'actualisation.

Nous introduisons le coefficient d'actualisation k = (1 + r) et considérons le montant des paiements actualisés P en fonction de k :

$$$$ afficher $$ \ commencer {équation} P (k) = \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~ ~~~~ (2) \ end {equation} $$ display $$

En différenciant P par rapport à k, on obtient

$$$$ afficher $$ \ commencer {équation} P '(k) = - \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} = - \ frac {1} {k} \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~~ (3) \ end {equation} $$ display $$

Compte tenu de ce dernier, l'expression de la durée de l'obligation prend la forme

$$$$ affiche $$ \ begin {equation} D = -k \ frac {P '(k)} {P (k)} ~~~~~~~~~~~~~ (4) \ end {equation} $$ afficher $$

Dans le même temps, nous rappelons que comme taux d'actualisation r dans le cas d'une obligation, le rendement à l'échéance (YTM) est utilisé.

L'expression obtenue est valable pour une obligation, mais nous nous intéressons à un portefeuille d' obligations. Passons maintenant à la détermination de la durée du portefeuille.

Nous introduisons la notation suivante:

• P _i est le prix de la i-ème obligation;
• z _i - le nombre de titres de la i-ème obligation en portefeuille;
• k _i - coefficient d'actualisation de la i-ème obligation du portefeuille;
• $$$ inline $ \ begin {equation} P_p = \ sum_ {i} {z_iP_i} \ end {equation} $ inline $ - prix du portefeuille;
• $$$ inline $ \ begin {equation} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} \ end {equation} $ inline $ - le poids de la ième obligation dans le portefeuille; exigence évidente$$ $ inline $ \ begin {equation} \ sum_ {i} w_i = 1 \ end {equation} $ inline $ ;
• $$$ inline $ \ begin {equation} k_p = \ sum_ {i} w_ik_i \ end {equation} $ inline $ - coefficient d'actualisation du portefeuille;

En raison de la linéarité de la différenciation, ce qui suit est vrai:

$$$$ afficher $$ \ commencer {équation} P'_p (k) = \ gauche (\ sum_ {i} z_iP_i (k) \ droite) '= \ sum_ {i} z_iP'_i (k) ~~~~~ ~~~~~~~~ (5) \ end {équation} $$ display $$

Ainsi, compte tenu des points (4) et (5), la durée du portefeuille peut être exprimée en

$$$$ afficher $$ \ commencer {équation} D_p = -k_p \ frac {P'_p} {P_p} = - \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} z_jP'_j} {\ sum_ {j} z_jP_j} \ à droite) ~~~~~~~~~~~~~~ (6) \ end {équation} $$ display $$

De (4), il suit sans ambiguïté$$ $ inline $ \ begin {equation} P'_j = - \ frac {D_jP_j} {k_j} \ end {equation} $ inline $ .
En substituant cette expression dans (6), nous arrivons à la formule suivante pour la durée du portefeuille:

$$$$ afficher $$ \ commencer {équation} D_p = \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} \ frac {D_j} {k_j} z_jP_j} {\ sum_ {j} z_jP_j} \ droite) = \ left (\ sum_ {i} w_ik_i \ right) \ left (\ sum_ {j} w_j \ frac {D_j} {k_j} \ right) ~~~~~~~~~~~~~ (7) \ fin {équation} $$ afficher $$

Dans les conditions où la durée et le rendement à l'échéance de chaque instrument sont connus (et nous rappelons que nous sommes dans de telles conditions), l'expression (7) est la formule souhaitée pour déterminer la durée d'un portefeuille en fonction de la durée de ses obligations. Cela ne semble compliqué qu'en apparence, mais en fait, il est déjà prêt pour une utilisation pratique à l'aide des fonctions les plus simples de MS Excel, que nous allons maintenant faire avec un exemple.

Exemple

Pour calculer la durée du portefeuille selon la formule (7), nous avons besoin de données d'entrée qui incluent l'ensemble réel des titres inclus dans le portefeuille, leurs durées et leur rendement à l'échéance. Comme mentionné ci-dessus, ces informations sont accessibles au public, par exemple, sur le site Web rusbonds.ru dans la section analyse des obligations. Les données source peuvent être téléchargées au format Excel.

Prenons par exemple un portefeuille de titres composé de 9 obligations. Le tableau de données d'origine téléchargé à partir de rusbonds a la forme suivante.



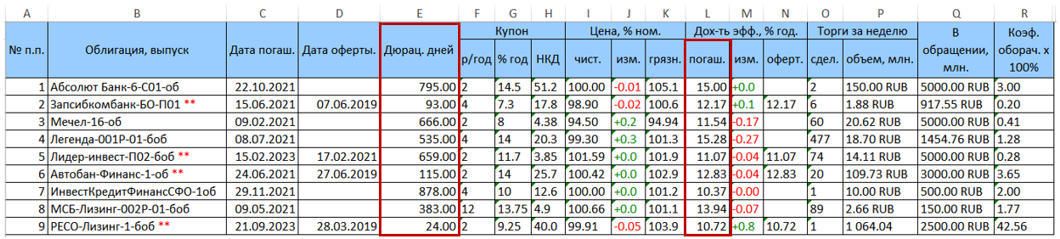
Deux colonnes qui nous intéressent avec une durée (colonne E) et un rendement à maturité (colonne L = YTM) sont surlignées en rouge.

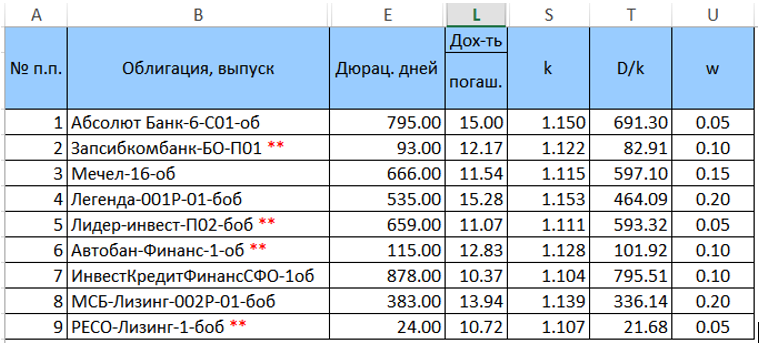
Nous fixons les pondérations w pour les obligations de ce portefeuille (jusqu'à présent de manière arbitraire, mais pour que leur somme soit égale à l'unité) et calculons k = (1 + YTM / 100) et D / k = («colonne E» / k). La table convertie (sans colonnes supplémentaires) ressemblera à



Ensuite, nous calculons le produit$$ $ inline $ \ begin {equation} w_j \ frac {D_j} {k_j} \ end {equation} $ inline $ et$$ $ inline $ \ begin {equation} w_ik_i \ end {equation} $ inline $ et les additionner, et multiplier les montants résultants par l'un par l'autre. Le résultat de cette multiplication sera la durée souhaitée pour une distribution donnée des poids.



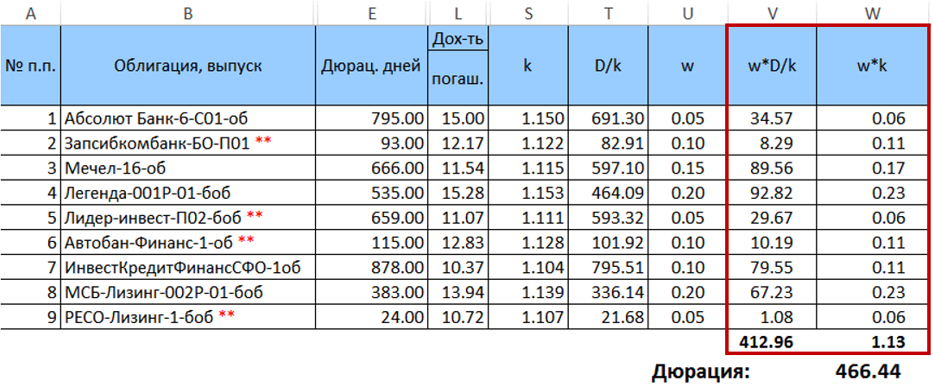
La durée souhaitée du portefeuille est donc de 466,44 jours. Il est important de noter que dans ce cas particulier, la durée calculée par la formule (7) est très légèrement différente de la durée moyenne pondérée calculée avec les mêmes poids (écart <0,5 jours). Cependant, cette différence augmente avec une augmentation de la dispersion des poids. Il augmentera également avec une augmentation de l'étalement des durées de papier.

Après avoir obtenu la formule de calcul de la durée du portefeuille, l'étape suivante consiste à déterminer le poids des titres afin qu'à un rendement donné la durée estimée du portefeuille soit minimale. Nous passons à la partie suivante - l'optimisation du portefeuille.

Partie 2. Optimisation du portefeuille obligataire

L'expression (7) est une forme quadratique, avec la matrice

$$$$ afficher $$ \ commencer {équation} A = \ gauche \ {k_i \ frac {D_j} {k_j} \ droite \} = \ commencer {pmatrix} D_1 & \ ldots & k_1 \ frac {D_n} {k_n} \ \ \ vdots & D_j & \ vdots \\ k_n \ frac {D_1} {k_1} & \ ldots & D_n \ end {pmatrix} \ end {equation} $$ display $$

En conséquence, sous forme matricielle, l'expression de la durée du portefeuille (7) peut s'écrire comme suit:

$$$$ afficher $$ \ commencer {équation} D_p = w ^ TAw ~~~~~~~~~~~~~ (8) \ fin {équation} $$ afficher $$

où w est le vecteur colonne des pondérations obligataires dans le portefeuille. Comme mentionné ci-dessus, la somme des éléments du vecteur w doit être égale à l'unité. D'un autre côté, l'expression $$$k_p = \ sum_ {i} w_i k_i$(qui, en substance, est un simple produit scalaire ( w , k ) , où k est le vecteur des coefficients d'actualisation des obligations) doit être égal au taux d'actualisation cible du portefeuille et, par conséquent, le rendement du portefeuille cible doit être défini.

Ainsi, la tâche d'optimisation d'un portefeuille obligataire est de minimiser la fonction quadratique (8) avec des contraintes linéaires.

La méthode classique pour trouver l'extrémum conditionnel d'une fonction de plusieurs variables est la méthode du multiplicateur de Lagrange. Cependant, cette méthode n'est pas applicable ici, ne serait-ce que parce que la matrice A est dégénérée par construction (mais pas seulement à cause de cela; nous omettons ici les détails de l'analyse de l'applicabilité de la méthode Lagrange afin de ne pas surcharger l'article avec un contenu mathématique excessif).

L'incapacité d'appliquer une méthode analytique facile et abordable conduit à la nécessité d'utiliser des méthodes numériques. Le problème de l'optimisation d'une fonction quadratique est bien connu et comporte plusieurs algorithmes efficaces développés depuis longtemps et mis en œuvre dans les bibliothèques publiques.

Pour résoudre ce problème particulier, la bibliothèque ALGLIB et les algorithmes d'optimisation quadratiques qui y sont implémentés, QP-Solvers , inclus dans le package minqp, ont été utilisés.

Le problème d'optimisation quadratique en général est le suivant:

Il est nécessaire de trouver un vecteur à n dimensions w minimisant la fonction

$$$$ afficher $$ \ commencer {équation} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~~ (9) \ end {equation} $$ afficher $$

Avec des restrictions données
1) l ≤ w ≤ u ;
2) Cw * d ;
où w, l, u, d, b sont des vecteurs à n dimensions réelles, Q est la matrice symétrique de la partie quadratique et le signe * signifie l'une des relations ≥ = ≤.
Comme le montre (8), la partie linéaire b ^T w dans notre fonction objectif est égale à zéro. Cependant, la matrice A n'est pas symétrique, ce qui n'empêche cependant pas de l'amener à une forme symétrique sans changer la fonction elle-même. Pour ce faire, il suffit de mettre au lieu de A l' expression$$ $ inline $ \ begin {equation} \ frac {A ^ T + A} {2} \ end {equation} $ inline $ Étant donné que la formule (9) inclut le coefficient $$$\ frac {1} {2}$alors nous en tant que Q nous pouvons accepter $$$A ^ T + A$.

Les coordonnées des vecteurs l et u spécifient les limites du vecteur souhaité et se situent dans l'intervalle [-1,1]. Puisque nous ne supposons pas de ventes à découvert d'obligations, les coordonnées des vecteurs dans notre cas ne sont pas toutes inférieures à 0. Dans le programme d'exemple ci-dessous, pour simplifier, le vecteur l est supposé être nul et les coefficients du vecteur u sont tous de 0,3 . Cependant, rien ne nous empêche d'améliorer le programme et de rendre les vecteurs de contraintes plus personnalisables.

La matrice C dans notre cas comprendra deux lignes: 1) les coefficients d'actualisation qui, lorsqu'ils sont multipliés de façon scalaire par les pondérations (les mêmes ( w , k )), devraient donner le taux de rendement cible du portefeuille; 2) une chaîne composée d'unités. Il est nécessaire de fixer des limites $$$\ sum_ {i} w_i = 1$.

Ainsi, l'expression Cw * d pour notre tâche ressemblera à ceci:

$$$$ afficher $$ \ begin {equation} \ left \ {\ begin {array} {ccc} ({\ bf w, k}) = k_p \\ \ sum_ {i} w_i = 1 \\ \ end {array} \ à droite. ~~~~~~~~~~~~~ (10) \ end {équation} $$ afficher $$

Nous passons maintenant à l'implémentation logicielle de la recherche du portefeuille optimal. La base de l'optimiseur quadratique dans ALGLIB est l'objet $$$\ tt \ small minqpstate$

alglib::minqpstate state; 

Pour initialiser l'optimiseur, cet objet est passé à la fonction minqpcreate avec le paramètre de dimension de tâche n

 alglib::minqpcreate(n, state); 

Le prochain point le plus important est le choix de l'algorithme d'optimisation (solveur). La bibliothèque ALGLIB pour l'optimisation quadratique propose trois solveurs:

• QP-BLEIC est l'algorithme le plus universel conçu pour résoudre des problèmes avec un nombre de contraintes linéaires peu élevé (jusqu'à 50 selon les recommandations de la documentation) (de la forme Cw * d ). Dans le même temps, il peut être efficace sur des tâches de grande dimension (comme le prétend la documentation - jusqu'à n = 10000).
• QuickQP est un algorithme très efficace, surtout lorsqu'une fonction convexe est optimisée. Cependant, malheureusement, il ne peut pas fonctionner avec des contraintes linéaires - uniquement avec des conditions aux limites (de la forme l≤w≤u ).
• Dense-AUL - optimisé pour le cas de très grandes dimensions et d'un grand nombre de restrictions. Mais, selon la documentation, les tâches de petite dimension et le nombre de restrictions seront résolus plus efficacement en utilisant d'autres algorithmes.

Compte tenu des caractéristiques ci-dessus, il est évident que le solveur QP-BLEIC convient le mieux à notre tâche.

Pour demander à l'optimiseur d'utiliser cet algorithme, vous devez appeler la fonction $$$\ tt \ small minqpsetalgobleic$. L'objet lui-même et les critères d'arrêt sont passés à cette fonction, sur laquelle nous ne nous attarderons pas plus en détail: dans le programme considéré ici, les valeurs par défaut sont utilisées. L'appel de fonction est le suivant:

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

L'initialisation supplémentaire du solveur comprend:

• Le transfert de la matrice de la partie quadratique Q - $$$\ tt \ small alglib :: minqpsetquadraticterm (état, qpma);$
• La transmission du vecteur de la partie linéaire (dans notre cas, le vecteur zéro) - $$$\ tt \ small alglib :: minqpsetlinearterm (état, b);$
• Le transfert des vecteurs de conditions aux limites l et u - $$$\ tt \ small alglib :: minqpsetbc (état, bndl, bndu);$
• Transmission linéaire - $$$\ tt \ small alglib :: minqpsetlc (état, c, ct);$
• Définition de l'échelle de coordonnées de l'espace vectoriel $$$\ tt \ small alglib :: minqpsetscale (état, s);$

Arrêtons-nous sur chaque élément:
Pour spécifier des vecteurs et des matrices, la bibliothèque ALGLIB utilise des objets de types spéciaux (entiers et réels): $$$\ tt \ small alglib :: integer \ _1d \ _array$, $$$\ tt \ small alglib :: real \ _1d \ _array$, $$$\ tt \ small alglib :: integer \ _2d \ _array$, $$$\ tt \ small alglib :: real \ _2d \ _array$. Pour préparer la matrice, nous avons besoin d'un type $$$\ tt \ small real \ _2d \ _array$. Dans le programme, créez d'abord une matrice A ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpma$), puis selon la formule $$$Q = A ^ T + A$on en construit la matrice Q ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpmq$) La définition des dimensions de la matrice dans ALGLIB est une fonction distincte $$$\ tt \ small setlength (n, m)$.

Pour construire les matrices, nous avons besoin du vecteur des coefficients d'actualisation ( k _i ) et de la relation de durée avec ces coefficients ( $$$\ frac {D_j} {k_j}$):

 std::vector<float> disfactor; std::vector<float> durperytm; 

L'extrait de code qui implémente la construction de matrices est illustré dans la liste suivante:

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

Le vecteur de la partie linéaire, comme déjà indiqué, est nul dans notre cas, donc tout est simple avec lui:

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

Les conditions aux limites des vecteurs sont transmises par une fonction. Pour résoudre ce problème, des conditions aux limites très simples sont appliquées: le grammage de chaque papier ne doit pas être inférieur à zéro (nous n'autorisons pas les positions négatives) et ne doit pas dépasser 30%. Si vous le souhaitez, les restrictions peuvent être compliquées. Des expériences avec le programme ont montré que même un simple changement dans cette plage peut affecter considérablement les résultats. Ainsi, une augmentation de la limite inférieure et / ou une diminution de la limite supérieure conduit à une plus grande diversification du portefeuille final, car lors de l'optimisation, un solveur peut exclure certains titres du vecteur résultant (leur attribuer un poids de 0%) comme ne convenant pas. Si vous définissez la limite inférieure des échelles, disons à 5%, tous les papiers sont garantis pour être inclus dans le portefeuille. Cependant, la durée calculée à de tels paramètres sera, bien sûr, plus longue que dans le cas où l'optimiseur peut exclure le papier.

Ainsi, les conditions aux limites sont définies par deux vecteurs et transférées au solveur:

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

Ensuite, l'optimiseur doit passer les contraintes linéaires spécifiées par le système (10). Dans ALGLIB, cela se fait en utilisant la fonction $$$\ tt \ small alglib :: minqpsetlc (état, c, ct)$, où c est la matrice combinant les côtés gauche et droit du système (10), c'est-à-dire voir la matrice $$$(C ~~ d)$, et ct est le vecteur de relations (c'est-à-dire les correspondances de la forme ≥, = ou ≤). Dans notre cas, ct = (0,0), ce qui correspond au rapport '=' pour les deux rangées de système (10).

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

La documentation de la bibliothèque ALGLIB recommande fortement de définir l'échelle des variables avant de démarrer l'optimiseur. Cela est particulièrement important si les variables sont mesurées en unités, dont le changement diffère selon les ordres de grandeur (par exemple, lors de la recherche d'une solution, les tonnes peuvent être modifiées en centièmes ou millièmes et en mètres en unités; le problème peut être résolu dans l'espace tonne-mètre), ce qui affecte les critères d'abandon. Il existe toutefois une réserve selon laquelle, avec la même mise à l'échelle des variables, la définition de l'échelle n'est pas nécessaire. Dans le programme à l'étude, nous poursuivons toujours la tâche d'échelle pour une plus grande rigueur de l'approche, d'autant plus que c'est très simple à faire.

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

Ensuite, nous définissons l'optimiseur comme point de départ. En général, cette étape est également facultative et le programme réussit à exécuter la tâche sans point de départ clairement défini. De même, pour des raisons de rigueur, nous fixons le point de départ. Nous ne serons pas intelligents: le point de départ sera le point avec les mêmes poids pour toutes les obligations.

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

Il reste à déterminer la variable dans laquelle l'optimiseur renverra la solution trouvée et la variable d'état. Ensuite, vous pouvez exécuter l'optimisation et traiter le résultat

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

Surtout, le temps d'exécution du programme n'a pas été mesuré dans les expériences, mais tout fonctionne très rapidement. Dans le même temps, il est clair qu'un investisseur privé est peu susceptible d'optimiser un portefeuille de plus de 10 à 15 obligations.

Il est également important de noter ce qui suit. L'optimiseur renvoie précisément le vecteur des poids. Pour obtenir la durée calculée elle-même, vous devez utiliser directement la formule (8). Le programme peut le faire. A cet effet, deux fonctions de multiplication des vecteurs et des matrices ont été spécialement ajoutées. Nous ne les donnerons pas ici. Ceux qui le souhaitent se retrouveront facilement dans les codes sources publiés.

C’est tout. Un investissement efficace dans des titres de créance pour tous.

PS Comprendre que choisir le code de quelqu'un d'autre n'est pas la profession la plus attrayante, et pour beaucoup de gens qui veulent investir, ce n'est pas du tout spécialisé, j'essaierai de déplacer ce programme un peu plus tard sous la forme d'un service Web simple que tout le monde peut utiliser, indépendamment des connaissances en mathématiques et programmation.