 Traduction originale dans mon blog
Traduction originale dans mon blogSteven Wolfram Live Contest Broadcast (en anglais) Site Web du concoursExpliquons aux lecteurs ce que signifie «Règle 30» - il s'agit d'un automate cellulaire élémentaire (voir Wiki ), dont l'état (la règle pour construire un nouveau niveau de cellules basé sur l'ancien) dans le système de nombres binaires est défini comme 0-0-0-1-1-1-1 -1-0, qui peut être interprété comme 30 en notation décimale.
Alors, où tout a-t-il commencé? - «Règle 30»
Comment se fait-il qu'une chose
incroyablement simple produise quelque chose d'incroyablement complexe ? Cela fait près de 40 ans que je me
suis familiarisé avec la Règle 30, mais cela m'étonne encore et me ravit. Pendant longtemps, c'est devenu ma découverte préférée dans l'
histoire de la science, au fil des ans, cela a changé ma vision du monde et m'a conduit à une
variété de nouveaux types de compréhension de la science, de la technologie, de la philosophie et bien plus encore .
Mais même après tant d'années, il y a encore de nombreux concepts de base sur la règle 30 qui nous restent inaccessibles. J'ai donc décidé qu'il était temps de tout faire pour stimuler le processus d'identification de l'ensemble de base de ces modèles de base.
Donc, aujourd'hui, j'offre aux candidats 30 000 $ comme prix total pour répondre aux trois questions principales concernant la règle 30.
La règle 30 est extrêmement simple:
Il existe une séquence de rangées de cellules noires et blanches (cellules) et, en tenant compte d'une rangée spécifique de cellules noires et blanches, les couleurs des cellules de la rangée ci-dessous sont déterminées, en considérant chaque cellule individuellement et ses cellules adjacentes adjacentes, puis la règle de substitution simple suivante leur est appliquée, à savoir:

CodeRulePlot[CellularAutomaton[30]]
[Regardez la vidéo qui, en quelques minutes, raconte l'essence des automates cellulaires et la règle 30 - note du traducteur]
Que se passe-t-il si vous commencez avec une seule cellule noire? [Une
ligne de cellules blanches est prise, infinie des deux côtés et une cellule noire, puis les règles ci-dessus s'appliquent à cette ligne, une nouvelle ligne est obtenue, etc. - Note du traducteur ] Supposons (comme je l'ai fait moi-même au début) que la règle est assez simple, et le modèle obtenu sur la base de son travail devrait également être simple. Cependant, si vous menez une expérience, vous verrez ce qui se passe après les 50 premières étapes de l'algorithme:

CodeRulePlot[CellularAutomaton[30], {{1}, 0}, 50, Mesh -> All,
ImageSize -> Full]
Naturellement, nous pouvons supposer qu'à la suite de l'algorithme, un objet mathématique beaucoup plus simple sera obtenu. Cependant, voici ce qui se passe après les 300 premières étapes:

Cela montre qu'il existe un certain
modèle - sur le côté gauche de la pyramide . Mais en même temps, de nombreux aspects de ce modèle
ressemblent à quelque chose de aléatoire .
Il est incompréhensible qu'une règle aussi simple puisse finalement conduire à un comportement système aussi complexe. Sur cette base, je suis parvenu à la conclusion
que dans l'univers informatique de tous les programmes informatiques possibles, ce comportement est assez courant, d'autant plus qu'il se retrouve presque partout.
Sur la base de cette hypothèse, j'ai développé une approche de la formation d'un tout
nouveau type de science - basée sur les
principes d' observation du fonctionnement d'algorithmes simples.
Progressivement, de plus en plus de preuves s'accumulaient sur ces principes.
Revenons cependant à la règle 30 et examinons en détail ce qu'elle nous permet exactement de faire et quelle est son utilisation? Que dire exactement du comportement de cet algorithme? Il est immédiatement évident que même les réponses aux questions les plus évidentes s'avèrent difficiles.
Même après des décennies pour lesquelles aucune réponse n'a été trouvée, j'ai décidé qu'il était temps de poser des questions spécifiques sur la règle 30, tout en stimulant ce domaine avec de sérieux prix en espèces.
J'ai déjà essayé de faire quelque chose de similaire en 2007, en
fixant un prix pour avoir répondu à la question de base sur une
machine Turing spécifique. Et dans ce cas, le résultat a été positif et n'a pas tardé à attendre. Quelques mois plus tard, ce
prix a été remporté - après avoir établi pour toujours ce qu'est la plus simple des machines Turing universelles possibles, et aussi prouver de manière très convaincante le
principe général
d'équivalence informatique , que j'ai personnellement développé plus tôt.
Le concours de la règle 30 se fixe une fois de plus l'objectif de résoudre une tâche clé, à savoir:
quelle est la complexité du comportement de la règle 30 ? Chacune des tâches pose une question dans ce domaine à sa manière et en particulier. Comme la règle 30 elle-même, ils sont tous d'une simplicité trompeuse dans leur cadre d'origine. Néanmoins, la solution à l'un d'entre eux sera une énorme réussite, qui contribuera finalement à éclairer les principes fondamentaux des propriétés de la formation de l'univers informatique, qui vont bien au-delà des spécificités de la règle 30.
Je
travaille sur chacune de ces questions depuis plus de 35 ans . Et pendant tout ce temps, j'ai essayé de trouver la bonne idée dans le cadre d'une pensée mathématique ou informatique cohérente, dans le but de résoudre enfin au moins un de ces problèmes. Maintenant, je veux ouvrir ce processus à toute la communauté mondiale. Cependant, je serai intéressé de savoir ce qui peut être réalisé pour résoudre ces problèmes et quelles méthodes peuvent être utilisées dans ce cas.
Règle 30 - Tâches à résoudre
Quant aux tâches compétitives selon la Règle 30, je donne la priorité à l'une des caractéristiques clés de l'algorithme de la Règle 30, à savoir: le
caractère aléatoire évident de la formation des cellules de sa colonne centrale . Commencez avec une cellule noire, puis regardez la séquence des valeurs de couleur des cellules dans cette colonne et vous arriverez à la conclusion qu'elles sont aléatoires:

CodeArrayPlot[
MapIndexed[If[#2[[2]] != 21, # /. {0 -> 0.2, 1 -> .6}, #] &,
CellularAutomaton[30, {{1}, 0}, 20], {2}], Mesh -> All]
Mais dans quel sens sont-ils
"vraiment aléatoires" ? Et cette hypothèse peut-elle être prouvée? Chacune des tâches définies dans le cadre du concours utilise son propre critère de hasard, puis demande si la séquence est aléatoire selon ce critère.
Tâche 1: la colonne centrale reste-t-elle toujours non périodique?
Considérez le début de la colonne centrale de la règle 30:

CodeArrayPlot[List@CellularAutomaton[30, {{1}, 0}, {80, {{0}}}],
Mesh -> True, ImageSize -> Full]
Il n'est pas difficile de trouver que les valeurs de cette colonne ne sont pas répétées - ce n'est pas périodique. Mais le défi est, la colonne centrale deviendra-t-elle jamais périodique du tout? En lançant la règle 30, nous voyons que la séquence ne devient pas périodique, même au
premier milliard d'étapes . Ce qui doit être fait pour établir et prouver cela avec certitude.
Voici le lien où se trouvent le
premier million et le
premier milliard de valeurs de cette séquence (
entrepôt de données Wolfram ).
Tâche 2: Chaque couleur de la cellule (noir ou blanc) est-elle en moyenne également probable dans la colonne centrale?
C'est ce que nous obtenons lorsque nous comptons le nombre de cellules noires et blanches séquentiellement à plusieurs étapes dans la colonne centrale de l'algorithme de la règle 30:

CodeDataset[{{1, 1, 0, ""}, {10, 7, 3, 2.3333333333333335}, {100, 52, 48, 1.0833333333333333},
{1000, 481, 519, 0.9267822736030829}, {10000, 5032, 4968, 1.0128824476650564},
{100000, 50098, 49902, 1.0039276982886458}, {1000000, 500768, 499232,
1.003076725850907}, {10000000, 5002220, 4997780, 1.0008883944471345},
{100000000, 50009976, 49990024, 1.000399119632349},
{1000000000, 500025038, 499974962, 1.0001001570154626}}]
Les résultats sont certainement proches de l'égalité pour les cellules noires et blanches. Ici, la problématique (question du problème) est de
savoir si cette relation converge vers 1 avec un nombre croissant d'étapes dans le cycle .
Tâche 3: Le calcul de la nième cellule de la colonne centrale nécessite-t-il au moins O ( n ) opérations?
Pour trouver la
nième cellule dans la colonne centrale, vous pouvez toujours simplement exécuter la règle 30 pour
n étapes, en calculant les valeurs de toutes les cellules à l'intérieur du diamant sélectionné dans la figure ci-dessous:

CodeWith[{n = 100},
ArrayPlot[
MapIndexed[If[Total[Abs[#2 - n/2 - 1]] <= n/2, #, #/4] &,
CellularAutomaton[30, CenterArray[{1}, n + 1], n], {2}]]]
Mais si vous le faites directement, cela
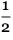 n 2
n 2 mises à jour de cellules distinctes, par conséquent, la puissance de calcul requise augmente à mesure que O (
n 2 ). La question de ce problème est de
savoir s'il existe une méthode plus (ou la plus) rapide pour calculer la valeur de la nième cellule sans tous les calculs intermédiaires - ou, en particulier, en moins de O ( n ) opérations .
Les chiffres qui composent Pi
La règle 30 est un produit de l'univers informatique: un système basé sur l'étude de programmes simples possibles avec une nouvelle structure intellectuelle, fournie par le paradigme de l'informatique. Cependant
, les tâches que j'ai définies dans le concours pour la règle 30 ont des analogues en mathématiques, qui existent depuis des siècles .
Considérez les
valeurs des nombres dans le nombre Pi . Le comportement de ces nombres est similaire à la génération de données dans la colonne centrale de l'algorithme de la règle 30. Autrement dit, il existe un algorithme donné pour les calculer, et une fois formulés, ils semblent presque aléatoires pour toutes les tâches.
![N [Pi, 85] N[Pi, 85]](https://habrastorage.org/getpro/habr/post_images/49e/ae6/17d/49eae617de3c0c9a864d4624413c6ce8.png)
Juste pour rendre l'analogue un peu plus proche, voici les premiers chiffres de Pi dans le système numérique avec base 2:
![BaseForm [N [Pi, 25], 2] BaseForm[N[Pi, 25], 2]](https://habrastorage.org/getpro/habr/post_images/18e/d4b/8f6/18ed4b8f6fd778443cc62470ea0956a9.png)
CodeBaseForm[N[Pi, 25], 2]
Et voici les premiers bits de la colonne centrale de la règle 30:
![Ligne [CellularAutomaton [30, {{1}, 0}, {90, {{0}}}] Row[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]](https://habrastorage.org/getpro/habr/post_images/9e9/f64/a52/9e9f64a521480621d3adbb859609742a.png)
CodeRow[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]
Pour le plaisir, vous pouvez les convertir en décimal:
![N [FromDigits [{Aplatir [CellularAutomaton [30, {{1}, 0}, {500, {0}}]], 0}, 2], 85] N[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]], 0}, 2], 85]](https://habrastorage.org/getpro/habr/post_images/0df/d67/782/0dfd677828ca278c971d267948d88ad3.png)
CodeN[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]],
0}, 2], 85]
Bien sûr, les algorithmes bien connus pour calculer les chiffres de Pi sont beaucoup plus compliqués que la règle relativement simple de génération de cellules dans la colonne centrale de la règle 30. Alors, que savons-nous des chiffres de Pi?
Tout d'abord, nous savons qu'ils ne se répètent pas. Cela a été prouvé dans les années 60 du 18e siècle, quand il a été démontré
que Pi est un nombre irrationnel , car les seuls nombres dans lesquels les nombres sont répétés sont des nombres rationnels. (En
1882, il a également été
démontré que Pi est transcendantal , c'est-à-dire qu'il ne peut pas être exprimé à travers les racines des polynômes).
Quel genre d'analogie peut-on tirer de la formulation du problème 2? Savons-nous que dans une séquence de chiffres de
Pi, différents chiffres se produisent avec la même fréquence? À ce jour
, plus de
100 trillions de chiffres binaires ont été calculés - et les fréquences des chiffres mesurés sont très proches (dans les
40 premiers
trillions de chiffres binaires de Pi, le rapport des unités aux zéros est d'environ 0,99999998064). Mais lors du calcul de la limite, les fréquences seront-elles exactement les mêmes? Les scientifiques posent cette question depuis plusieurs siècles, mais jusqu'à présent, les mathématiques n'ont pas pu y répondre.
Pour les nombres rationnels, les séquences de chiffres qui les composent sont périodiques, et il est facile de déterminer les fréquences relatives d'occurrence de ces nombres dans un nombre. Cependant, pour la séquence de chiffres de tous les autres nombres «créés par la nature (naturellement construits)», dans la plupart des cas, on ne sait pratiquement rien de ce que les fréquences des chiffres inclus dans le nombre ont tendance. Il serait logique de supposer qu'en fait, les chiffres de Pi (ainsi que la colonne centrale de la règle 30) sont «
normaux » dans le sens où non seulement chaque chiffre individuel, mais aussi tout bloc de chiffres d'une longueur donnée se rencontrent avec une fréquence maximale égale. Et, comme cela a été noté dans les travaux sur ce sujet des années 30, il est tout à fait possible de "construire une construction numérique (modèle)" de nombres normaux.
La constante de Champernone obtenue en combinant les chiffres d'entiers consécutifs est un exemple du raisonnement ci-dessus (le même peut être obtenu sur la base de n'importe quel nombre normal en combinant les valeurs des fonctions d'entiers consécutifs):
![N [ChampernowneNumber [10], 85] N[ChampernowneNumber[10], 85]](https://habrastorage.org/getpro/habr/post_images/253/f93/8f3/253f938f3261e70f8985a49bf1158dde.png)
CodeN[ChampernowneNumber[10], 85]
Il convient de noter que le point ici est que pour les nombres «naturellement construits» formés par des combinaisons de fonctions mathématiques standard, aucun exemple découvert n'est trouvé où une séquence régulière de nombres serait trouvée. Naturellement, en fin de compte, cette disposition dépend de ce que l'on entend par «régularité» et, à un certain stade, la tâche se transforme en une sorte de recherche
numérique-analogique pour l'intelligence extraterrestre . Cependant, rien ne prouve qu'il ne soit pas possible, par exemple, de trouver une combinaison complexe de racines carrées qui aurait une séquence de nombres avec une régularité très évidente.
Alors, enfin, considérez l'analogue du problème 3 pour Pi? Contrairement à la règle 30, où la façon évidente de calculer les éléments dans une séquence est une étape à la fois, les méthodes traditionnelles de calcul des chiffres de Pi incluent l'obtention des meilleures approximations de Pi en tant que nombre exact. Avec la série standard ("bizarre") inventée par
Ramanujan en 1910 et améliorée
par les frères Chudnovsky en 1989, les premiers membres de cette série donnent les approximations suivantes:

CodeStyle[Table[N[(12*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(n\)]
\*FractionBox[\(
\*SuperscriptBox[\((\(-1\))\), \(k\)]*\(\((6*k)\)!\)*\((13591409 +
545140134*k)\)\), \(\(\((3*k)\)!\)
\*SuperscriptBox[\((\(k!\))\), \(3\)]*
\*SuperscriptBox[\(640320\), \(3*k + 3/2\)]\)]\))^-1, 100], {n, 10}] //
Column, 9]
Alors, combien d'opérations sont nécessaires pour trouver le
nième chiffre? Le nombre de termes requis dans la ligne est O (
n ). Mais chaque condition doit être calculée avec une précision à
n chiffres, ce qui nécessite au moins O (
n ) opérations de calcul distinctes, ce qui implique qu'en général les charges de travail de calcul seront supérieures à O (
n ).
Jusqu'aux années 1990, on supposait qu'il n'y avait aucun moyen de calculer le
nième chiffre de Pi sans calculer tous les précédents. Mais en 1995,
Simon Pluff a découvert qu'il est effectivement possible de calculer, bien qu'avec une certaine probabilité, le
nième chiffre sans calculer les précédents. Et bien que l'on puisse penser que cela vous permettrait d'obtenir le
nième chiffre en moins de O (
n ) opérations, le fait que vous ayez besoin d'effectuer des calculs avec une précision de
n chiffres signifie qu'au moins
O ( n ) opérations.
Résultats, analogies et intuition
Tâche 1: la colonne centrale reste-t-elle toujours non périodique?
Des trois prix du concours Rule 30, c'est celui dans lequel la plupart des progrès dans la résolution de ce problème ont déjà été réalisés. Comme on ne sait toujours pas si la colonne centrale de la Règle 30 deviendra périodique,
Erica Jen en 1986 a
montré que deux colonnes ne peuvent pas être périodiques. Et en fait, c'est le cas, et on peut également plaider en faveur du fait
qu'une colonne en combinaison avec des cellules individuelles dans une autre colonne ne peut pas être périodique .
La preuve de la paire de colonnes utilise une caractéristique de la règle 30. Considérez la structure de la règle:
![RulePlot [CellularAutomaton [30]] RulePlot[CellularAutomaton[30]]](https://habrastorage.org/getpro/habr/post_images/5fa/ca7/858/5faca785893d90e7969ef2a4dad73c58.png)
CodeRulePlot[CellularAutomaton[30]]
Il est possible de dire simplement que pour chaque triple de cellules, la règle détermine la couleur de la cellule centrale, mais pour la règle 30, vous pouvez également exécuter efficacement la règle sur le côté: en tenant compte de la cellule à droite et au-dessus, vous pouvez également déterminer de manière unique la couleur de la cellule à gauche. Cela signifie que si vous prenez deux colonnes adjacentes,
vous pouvez restaurer l'intégralité du modèle sur la gauche :

CodeGraphicsRow[
ArrayPlot[#, PlotRange -> 1, Mesh -> All, PlotRange -> 1,
Background -> LightGray,
ImageSize -> {Automatic, 80}] & /@ (PadLeft[#, {Length[#], 10},
10] & /@
Module[{data = {{0, 1}, {1, 1}, {0, 0}, {0, 1}, {1, 1}, {1,
0}, {0, 1}, {1, 10}}},
Flatten[{{data},
Table[Join[
Table[Module[{p, q = data[[n, 1]], r = data[[n, 2]],
s = data[[n + 1, 1]] },
p = Mod[-q - r - qr + s, 2];
PrependTo[data[[n]], p]], {n, 1, Length[data] - i}],
PrependTo[data[[-#]], 10] & /@ Reverse[Range[i]]], {i, 7}]},
1]])]
Cependant, si les colonnes avaient une structure périodique, il s'ensuivrait immédiatement que le modèle restauré devrait également être périodique. Ainsi, par exemple, par construction, au moins les conditions initiales ne sont certainement pas périodiques, et donc les deux colonnes ne peuvent pas être périodiques. La même affirmation est vraie si les colonnes ne sont pas adjacentes et si toutes les cellules des deux colonnes ne sont pas connues. Cependant, il n'existe aucun moyen connu de distribuer cette disposition pour une seule colonne, telle qu'une colonne centrale, et cela ne résout donc pas la première tâche du concours en vertu de la règle 30.
Alors, que peut-on utiliser pour le résoudre? S'il s'avère que la colonne centrale est finalement périodique, vous pouvez simplement la calculer. Nous savons que ce n'est pas périodique pour le premier milliard d'étapes, mais nous pouvons au moins supposer qu'il peut y avoir un processus de transition avec des milliards d'étapes, après quoi il devient périodique.
Pensez-vous que cela soit crédible?
Des transitoires se produisent - et théoriquement (comme dans le
problème classique
de l'arrêt d'une machine de Turing ), ils peuvent même être de longueur arbitraire. Ici, nous regardons un exemple - trouvé lors de la recherche -
Règles avec 4 couleurs possibles (code commun 150898). Supposons que nous exécutions 200 étapes et, comme vous pouvez le voir, la colonne centrale sera complètement aléatoire:

CodeArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {200, 150 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]},
PixelConstrained -> 2, Frame -> False]
Après 500 étapes, le modèle entier semble complètement aléatoire:

CodeArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {500, 300 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, Frame -> False,
ImagePadding -> 0, PlotRangePadding -> 0, PixelConstrained -> 1]
Ici, vous pouvez voir qu'à l'approche de la colonne centrale, quelque chose de surprenant se produit: après 251 étapes, la colonne centrale semble renaître à une valeur fixe (ou au moins fixée à plus d'un million de pas):

CodeGrid[{ArrayPlot[#, Mesh -> True,
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, ImageSize -> 38,
MeshStyle -> Lighter[GrayLevel[.5, .65], .45]] & /@
Partition[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {1400, {-4, 4}}],
100]}, Spacings -> .35]
La même transition pourrait-elle se produire dans la règle 30? Examinez les motifs de la règle 30 et sélectionnez ceux où les diagonales de gauche ont une périodicité:

Codesteps = 500;
diagonalsofrule30 =
Reverse /@
Transpose[
MapIndexed[RotateLeft[#1, (steps + 1) - #2[[1]]] &,
CellularAutomaton[30, {{1}, 0}, steps]]];
diagonaldataofrule30 =
Table[With[{split =
Split[Partition[Drop[diagonalsofrule30[[k]], 1], 8]],
ones = Flatten[
Position[Reverse[Drop[diagonalsofrule30[[k]], 1]],
1]]}, {Length[split[[1]]], split[[1, 1]],
If[Length[split] > 1, split[[2, 1]],
Length[diagonalsofrule30[[k]]] - Floor[k/2]]}], {k, 1,
2 steps + 1}];
transientdiagonalrule30 = %;
transitionpointofrule30 =
If[IntegerQ[#[[3]]], #[[3]],
If[#[[1]] > 1,
8 #[[1]] + Count[Split[#[[2]] - #[[3]]][[1]], 0] + 1, 0] ] & /@
diagonaldataofrule30;
decreasingtransitionpointofrule30 =
Append[Min /@ Partition[transitionpointofrule30, 2, 1], 0];
transitioneddiagonalsofrule30 =
Table[Join[
Take[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]] + 2,
Drop[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]]], {n, 1, 2 steps + 1}];
transientdiagonalrule30 =
MapIndexed[RotateRight[#1, (steps + 1) - #2[[1]]] &,
Transpose[Reverse /@ transitioneddiagonalsofrule30]];
smallertransientdiagonalrule30 =
Take[#, {225, 775}] & /@ Take[transientdiagonalrule30, 275];
Framed[ArrayPlot[smallertransientdiagonalrule30,
ColorRules -> {0 -> White, 1 -> Gray, 2 -> Hue[0.14, 0.55, 1],
3 -> Hue[0.07, 1, 1]}, PixelConstrained -> 1,
Frame -> None,
ImagePadding -> 0, ImageMargins -> 0,
PlotRangePadding -> 0, PlotRangePadding -> Full
], FrameMargins -> 0, FrameStyle -> GrayLevel[.75]]
Apparemment, il y a une bordure qui sépare l'ordre à gauche du trouble à droite. Et, au moins pour les 100 000 premiers pas environ, il semble que la frontière se déplace en moyenne d'environ 0,252 pas vers la gauche à chaque pas -
avec quelques écarts aléatoires :
Codedata = CloudGet[
CloudObject[
"https://www.wolframcloud.com/obj/bc470188-f629-4497-965d-\
a10fe057e2fd"]];
ListLinePlot[
MapIndexed[{First[#2], -# - .252 First[#2]} &,
Module[{m = -1, w},
w = If[First[#] > m, m = First[#], m] & /@ data[[1]]; m = 1;
Table[While[w[[m]] < i, m++]; m - i, {i, 100000}]]],
Filling -> Axis, AspectRatio -> 1/4, MaxPlotPoints -> 10000,
Frame -> True, PlotRangePadding -> 0, AxesOrigin -> {Automatic, 0},
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
Mais comment découvre-t-on finalement à quel point ces fluctuations cesseront d'être significatives, à tel point qu'elles obligent l'ordre de gauche à traverser la colonne centrale et, peut-être, à rendre périodique l'ensemble du modèle? À en juger par les données disponibles, l'hypothèse semble peu probable, alors que je ne peux pas dire exactement comment cela peut être déterminé.
C'est bien sûr précisément le cas qui illustre l'existence de systèmes avec des «transitoires» exceptionnellement longs. Considérons maintenant la distribution des nombres premiers et calculons
LogIntegral [
n ] -
PrimePi [
n ]
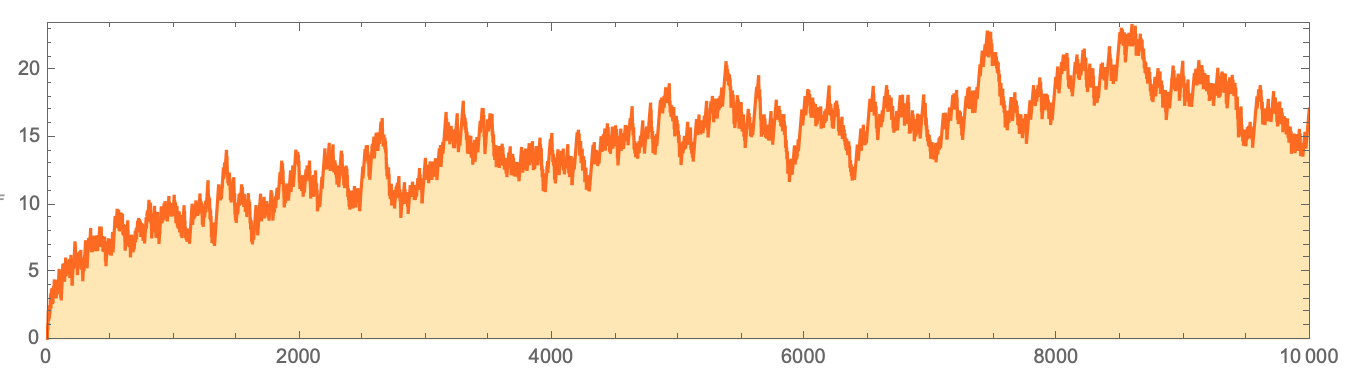
CodeDiscretePlot[LogIntegral[n] - PrimePi[n], {n, 10000},
Filling -> Axis,
Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4,
Joined -> True, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
Oui, il y a des fluctuations, mais dans cette illustration, il semble que cette différence sera toujours dans la zone positive. Et c'est, par exemple, ce dont parlait Ramanujan, mais finalement
il s'avère que ce n'est pas le cas . Au début, la limite de l'endroit où il a échoué était, à cette époque, astronomiquement grande (
Skives numéro 10
10 10 964 ). Et bien que personne n'ait encore trouvé de valeur explicite de
n pour laquelle la différence soit négative, on sait que jusqu'à
n = 10
317 elle doit exister (et finalement la différence sera négative).
Je suis d'avis que rien de ce genre n'arrive à la colonne centrale de l'article 30, mais jusqu'à présent, nous n'avons aucune preuve que cela est impossible, cela ne peut être soutenu.
Il convient de noter qu'il est possible de faire l'hypothèse que bien qu'il soit fondamentalement possible de prouver la périodicité en révélant la régularité dans la colonne centrale de la règle 30, rien de ce genre ne peut être fait pour la non-périodicité. Il est connu qu'il existe des motifs dont les colonnes centrales sont non périodiques, bien qu'elles soient très régulières. La classe principale de ces exemples sont les modèles imbriqués. Voici, par exemple, une illustration très simple de la règle 161, dans laquelle la colonne centrale a des globules blancs lorsque
n = 2
k :

CodeGraphicsRow[
ArrayPlot[CellularAutomaton[161, {{1}, 0}, #]] & /@ {40, 200}]
Et voici un
exemple légèrement plus complexe (de la règle bicolore 69540422 pour deux voisins) , dans lequel la colonne centrale est une
séquence Thue - Morse -
ThueMorse [
n ]:

CodeGraphicsRow[
ArrayPlot[
CellularAutomaton[{69540422, 2, 2}, {{1},
0}, {#, {-#, #}}]] & /@ {40, 400}]
On peut supposer que la séquence Thue - Morse est générée par l'application séquentielle de la substitution:

CodeRulePlot[SubstitutionSystem[{0 -> {0, 1}, 1 -> {1, 0}}],
Appearance -> "Arrow"]
Il s'avère que le
nième terme de cette séquence est défini comme
Mod [
DigitCount [
n , 2, 1], 2] - cet objet ne sera jamais périodique.
Se pourrait-il que la colonne centrale de la règle 30 puisse être générée par
remplacement ? Si tel est le cas, je serais étonné de ce fait (bien qu'il
semble y avoir des exemples naturels lorsque des systèmes de substitution très complexes apparaissent ), mais encore une fois, tant qu'il n'y a aucune preuve de cela.
Il convient de noter que toutes les tâches compétitives de la règle 30 sont prises en compte dans la formulation d'un algorithme qui s'exécute sur un nombre infini de cellules. ,
n , , ( )? , 2
n —
, , .
n =5:

Graph[# -> CellularAutomaton[30][#] & /@ Tuples[{1, 0}, 4],
VertexLabels -> ((# ->
ArrayPlot[{#}, ImageSize -> 30, Mesh -> True]) & /@
Tuples[{1, 0}, 4])]
=5
n =11:

Row[Table[
Framed[Graph[# -> CellularAutomaton[30][#] & /@
Tuples[{1, 0}, n]]], {n, 4, 11}]]
, , , , . , 2
n ( , ,
).
,
n 30 ,
, 2 n .
, ( ):
ListLogPlot[
Normal[Values[
ResourceData[
"Repetition Periods for Elementary Cellular Automata"][
Select[#Rule == 30 &]][All, "RepetitionPeriods"]]],
Joined -> True, Filling -> Bottom, Mesh -> All,
MeshStyle -> PointSize[.008], AspectRatio -> 1/3, Frame -> True,
PlotRange -> {{47, 2}, {0, 10^10}}, PlotRangePadding -> .1,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
, ,
n 2
0.63 n . , , . , , ? .
2: ?
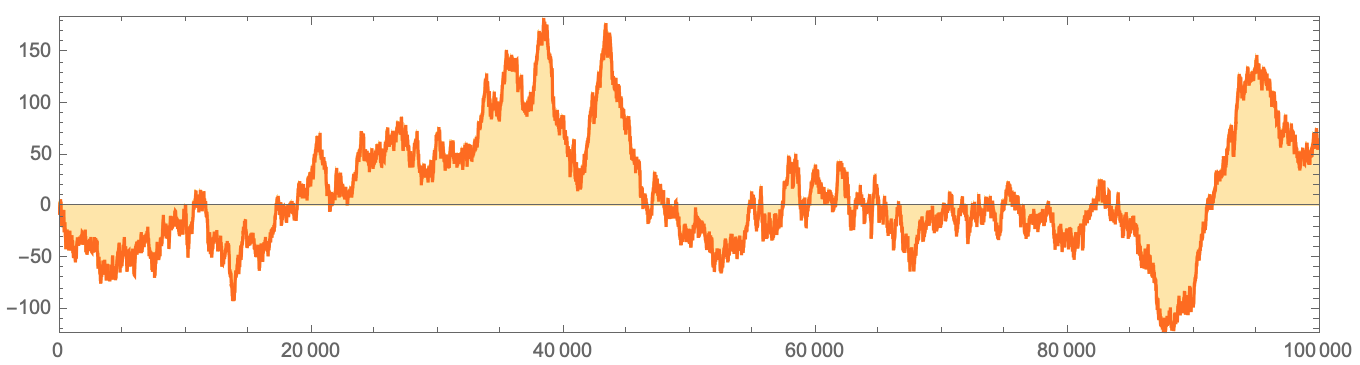
10000 30:
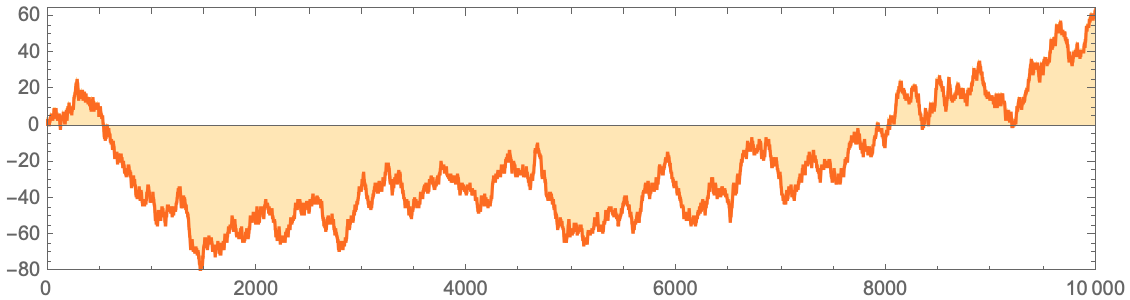
RListLinePlot[
Accumulate[2 CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}] - 1],
AspectRatio -> 1/4, Frame -> True, PlotRangePadding -> 0,
AxesOrigin -> {Automatic, 0}, Filling -> Axis,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
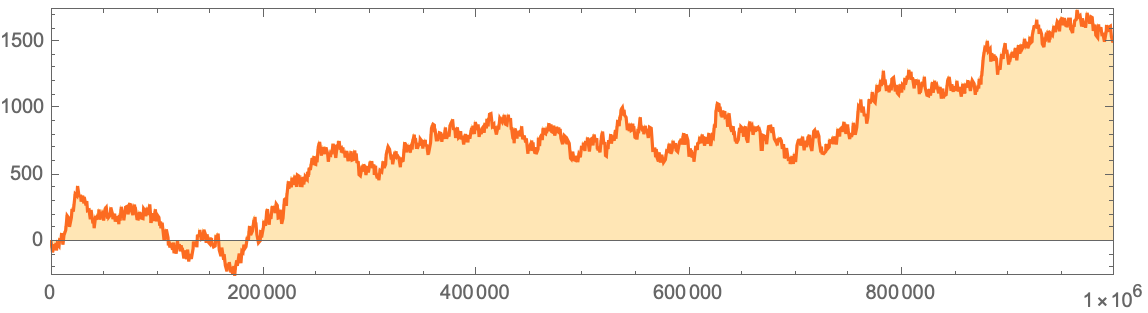
ListLinePlot[
Accumulate[
2 ResourceData[
"A Million Bits of the Center Column of the Rule 30 Cellular Automaton"] - 1], Filling -> Axis, Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4, MaxPlotPoints -> 1000, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
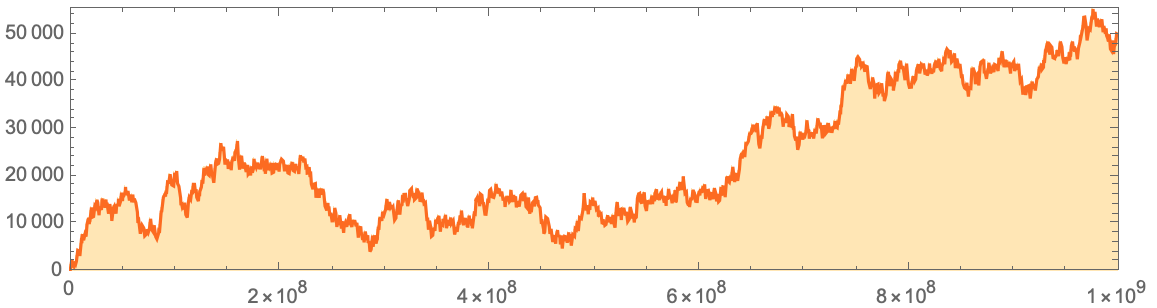
data=Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]];
data=Accumulate[2 data-1];
sdata=Downsample[data,10^5];
ListLinePlot[Transpose[{Range[10000] 10^5,sdata}],Filling->Axis,Frame->True,PlotRangePadding->0,AspectRatio->1/4,MaxPlotPoints->1000,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, , 1 () 0 (), , , , , , , .
. 10 000 :

Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.88, 1.04}}]]
, 1? …
, :
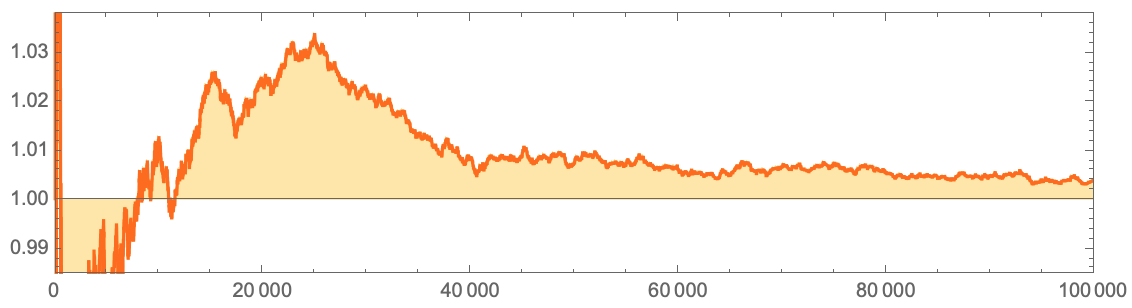
Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^5 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.985, 1.038}}]]
, , . 1 , :
accdata=Accumulate[Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]]];
diffratio=FunctionCompile[Function[Typed[arg,TypeSpecifier["PackedArray"]["MachineInteger",1]],MapIndexed[Abs[N[#]/(First[#2]-N[#])-1.]&,arg]]];
data=diffratio[accdata];
ListLogLogPlot[Join[Transpose[{Range[3,10^5],data[[3;;10^5]]}],Transpose[{Range[10^5+1000,10^9,1000],data[[10^5+1000;;10^9;;1000]]}]],Joined->True,AspectRatio->1/4,Frame->True,Filling->Axis,PlotRangePadding->0,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, ? . , . , , , , .
, , 30, .
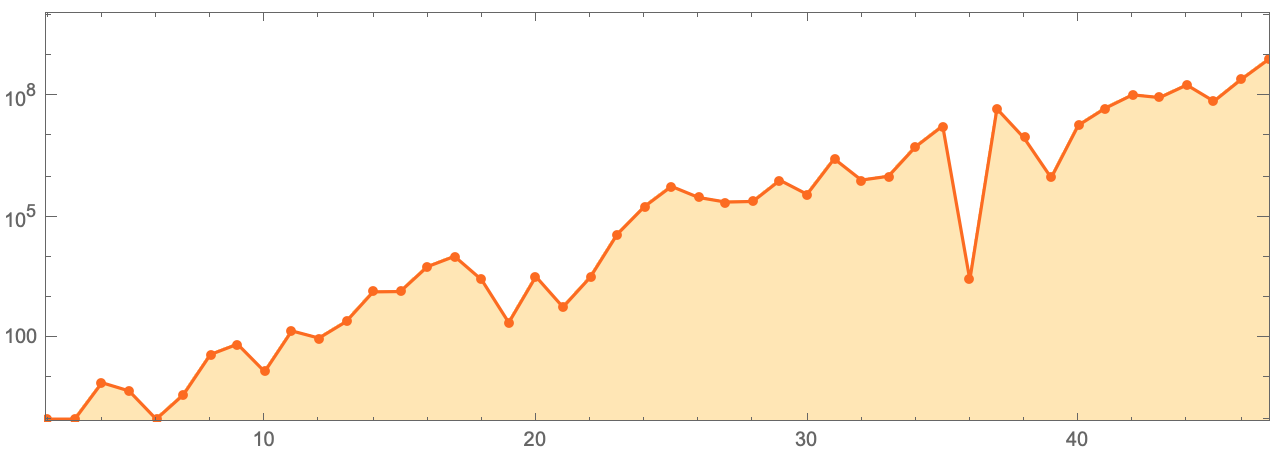
, ,
k . , 2
k . , - , , , , 30
k ( ).
,
. , ,
k =22, 2
k , , :

ListLogPlot[{3, 7, 13, 63, 116, 417, 1223, 1584, 2864, 5640, 23653,
42749, 78553, 143591, 377556, 720327, 1569318, 3367130, 7309616,
14383312, 32139368, 58671803}, Joined -> True, AspectRatio -> 1/4,
Frame -> True, Mesh -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.01]}],
PlotTheme -> "Detailed",
PlotStyle -> Directive[{Thickness[.004], Hue[0.1, 1, 0.99]}]]
, , . , –
, , .
—
— , , ,
, , , 30,
, ,
, , .
30 , , «
», , , , , , . , «»: 30, , , , , , , , 30.
, . 30, , - ,
, , 30, , , - .
. 30
, , . , , 30 - ( ), , , , 30. 200 :

ListLinePlot[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {200, {0, 200}}], Mesh -> All,
AspectRatio -> 1/4, Frame -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.0085]}],
PlotTheme -> "Detailed", PlotStyle -> Directive[{
Hue[0.1, 1, 0.99]}], ImageSize -> 575]
, :

Grid[{Table[
Histogram[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {10^n, {0, 20}}], {.01},
Frame -> True,
FrameTicks -> {{None,
None}, {{{0, "0"}, .2, .4, .6, .8, {1, "1"}}, None}},
PlotLabel -> (StringTemplate["`` steps"][10^n]),
ChartStyle -> Directive[Opacity[.5], Hue[0.09, 1, 1]],
ImageSize -> 208,
PlotRangePadding -> {{0, 0}, {0, Scaled[.06]}}], {n, 4, 6}]},
Spacings -> .2]
, , , 0 1.
1900- . , ,
FractionalPart [
hn ]
n h . ,
FractionalPart [
h n ]
h (
), —
FractionalPart [(3/2)
n ] — . (,
, 16- , , 2-
FractionalPart [16
x n -1 +
r [
n ]],
r [
n ]
n .)
3: n- O( n ) ?
,
150 :

Row[{ArrayPlot[CellularAutomaton[150, {{1}, 0}, 30], Mesh -> All,
ImageSize -> 315],
ArrayPlot[CellularAutomaton[150, {{1}, 0}, 200], ImageSize -> 300]}]
, ( ), , :

ArrayPlot[{Table[Mod[IntegerExponent[t, 2], 2], {t, 80}]},
Mesh -> All, ImageSize -> Full]
? , ,
:
Mod [
IntegerExponent [
n , 2], 2]. ,
n , , .
, « »? ,
n ,
Log [2,
n ] . , , O(log
n ) .
- 30? ,
n- , 30
n 2 , , . , -, , , — , , , , , .
« » (,
, . .), , , , , (,
,
3D- . .), .
,
1980- , , , ,
, , , .
, 3 30 , , . ( O(
n ) ; O(
n α ) α <2, , , O(log
β (
n )) — , , .)
3 , ,
n- , O(
n ), 150 .
O (
n )? () , « »?
, — — , , .
,
. , , ,
n , ,
,
n , (, «», O(log
n ) .
, . , , , ,
Wolfram Language . « ». , , Wolfram Language
, .
, 30 , 3 , , , , , ,
n- , O(
n ) , .
, , . , ,
. , , , , , — , O(log
n ) ,
n .
,
P NP . , 30 ( P
LOGTIME ), , , , . , , ,
n n , O(
n 2 ) , , P (« »), , , , , NP. («») , , , , 2
n .
, 2
n , , . ,
NP- , , , NP . 30 NP-? , , ( - , 30
NP).
30 . : 30 , , 30, «» , , , , .
, 256
110 ( , ),
110 , ,
, . , , , «» 110 .

SeedRandom[23542345]; ArrayPlot[
CellularAutomaton[110, RandomInteger[1, 600], 400],
PixelConstrained -> 1]
30, , — , «» , . ,
, 30 , , ,
, .
, , , , , 30. , , (, )
, , . , , — , . , .
, , 3.
,
,
,
,
n- ?
, 30 . , 2
m 2 m ×
m , , . , , , O(
n 2 ) ( ). , O(
n ) ? .
, 1 , , - O(
n ) — , « ». , ( , 2 ), , , .
- , , , ? ,
, .
. «» , , , .
30 - . ( — — 30
Wolfram Language, « !» ).
: «
- , , ». ? , , , - .
. , — , . ,
, , — - «» 30.
,
30. , 30 - . , , , - 30 , , , , — 30, , , , .
. ,
3 2 6 :

Row[Riffle[
ArrayPlot[#, ImageSize -> {Automatic, 275}] & /@ {Table[
IntegerDigits[3^t, 2, 159], {t, 100}],
Table[IntegerDigits[3^t, 6, 62], {t, 100}]}, Spacer[10]]]
, 6
. ( 2 ). , , .
s- n .
s- 3
n , «» (
b — , 2 6)
Mod [
Quotient [3
n , b
s ], b]. ? , 3
n n , : , , 3
n , log(
n ). , ,
, . , 30, , - , .
3
n -
30 , , O(
n ), ,
n , . ,
r [
n ] ,
r [
n ] «O-»
n , ,
MaxLimit [
r [
n ]/
n ,
n →∞ ]<∞.
, ( - ), . ,
r [
n ]
n , , , - , ,
r [
n ]
. , -
n ( - ),
r [
n ] . , , ,
r [
n ] O(
n ).
30
, ( , ).
Wolfram Language
t 30 :
![c[t_] c[t_]](https://habrastorage.org/getpro/habr/post_images/219/e07/f8e/219e07f8ec41111ce3457989e3d3c188.png)
c[t_] := CellularAutomaton[30, {{1}, 0}, {t, {{0}}}]
[
t ].
1: ?

\!\(
\*SubscriptBox[\(\[NotExists]\), \({p, i}\)]\(
\*SubscriptBox[\(\[ForAll]\), \(t, t > i\)]c[t + p] == c[t]\)\)

NotExists[{p, i}, ForAll[t, t > i, c[t + p] == c[t]]]
,
t >
i ,
[
t +
p ]
c [
t ].
2: ?

\!\(\*UnderscriptBox[\(\[Limit]\), \(t\*
UnderscriptBox["\[Rule]",
TemplateBox[{},
"Integers"]]\[Infinity]\)]\) Total[c[t]]/t == 1/2

DiscreteLimit[Total[c[t]]/t, t -> Infinity] == 1/2
[
t ]/
t t →∞ 1/2.
3: n- O( n ) ?
machine[
m ] ,
m (,
TuringMachine [...]), machine[
m ][
n ] {
v ,
t },
v — ,
t — (, ). :
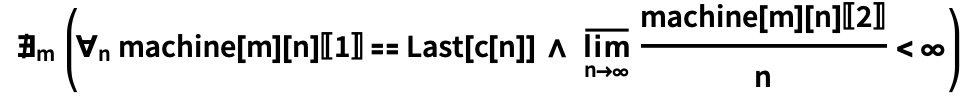
\!\(
\*SubscriptBox[\(\[NotExists]\), \(m\)]\((
\*SubscriptBox[\(\[ForAll]\), \(n\)]\(\(machine[m]\)[n]\)[[1]] ==
Last[c[n]]\ \[And] \
\*UnderscriptBox[\(\[MaxLimit]\), \(n -> \[Infinity]\)]
\*FractionBox[\(\(\(machine[m]\)[n]\)[[
2]]\), \(n\)] < \[Infinity])\)\)
« m, , machine[
m ]
n c [
n ] ,
n , ». (
m , «» ).
, , , , . 3 ( ), , 1 2, . 3 ( ), , 1 . :
1 , , 3 .
1 , , , , , 2. , 2 - 3. ,
, O(
n ) — , , 3, , .
, , ?
1 , , , 30 - , . , 1 , . , , - , .
( , ), 2, 3 , — , , , . , 3 , , (, , ), O(
n ) .
, - . ,
n n- . . , - , . , ,
n n . , . , « » . ,
n , . , , O(
n ) .
:
? « »,
/
( ).
, , (
)? , , , , «» , -, ( ) , .
, ,
. , , , . , () .
, , , , : «
». , , , .
, — - . -
n , . . — («
» . .). , , , .
— , , . , (
FindEquationalProof ). , ()
.
,
, , — , . — , .
, .
Wolfram|Alpha (, ) , . , .
, , -
, , , , .
? ,
«» , .
Wolfram Language , . Wolfram Language, .
« »? , , - . . - , , «» , , - ( ), . , , «» — , .
?
, ? . . , . - , . . - , , .
, , «» — , — , « ». ,
2,3 2007 .
— , , 30, , .
. - ( , , ). , , ( ) , , .
n — 30
n ,
n .
Wolfram Language . , 0,4 100 000 :

CellularAutomaton[30, {{1}, 0}, {100000, {{0}}}]; // Timing
,
30 Xor [
p ,
Or [
q ,
r ]],
.
,
CellularAutomaton :

Module[{a = 1},
Table[BitGet[a, a = BitXor[a, BitOr[2 a, 4 a]]; i - 1], {i,
100000}]]; // Timing
.
. , , 30, , 30 , , , : .
. , , «»
. 30 — . , , , .
— , , . , , 30, .
, , 30,
. 45° , 30, , . ; . ?
? ? - ?
, , , , , .
?
30, . , , ,
, ,
. , - , , ,
, , , - .
– , «» .
( , - ). , , , ,
« » :

GraphicsRow[(ArrayPlot[
CellularAutomaton[30,
MapAt[1 - #1 &, Flatten[Table[#1, Round[150/Length[#1]]]], 50],
100]] &) /@ {{1, 0}, {1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0}, {1,
0, 0, 0, 0, 0, 0}, {1, 1, 1, 0, 0}}]
, , , . ? , « » ?
, (, ), , - 30?
« 30». , «» ? 30 , ? «» ?
, , 30, , , , 30, . 256 ( ) , , :

Row[Riffle[
Labeled[ArrayPlot[CellularAutomaton[#, {{1}, 0}, {150, All}],
PixelConstrained -> 1, Frame -> False],
Style[Text[StringTemplate["rule ``"][#]], 12],
LabelStyle -> Opacity[.5]] & /@ {45, 73}, Spacer[8]]]
, . , . ,
, . , , , « 30», .
« 30». 30 ( 1), , — , .
2, 30, , .
3 .
n- O(
n γ ) γ <2 ( - )? ,
n- , O(log(
n )) ? O(log(
n )) ? ? . ?
, 30. 30, (, , 110) , 30.
, NP-, 30 , , NP-? , . , , , « », 30?
?
2007 2,3 , — , , , . , . 30? . 40 , - ( , !). , , (, ) .
, - ( ), , , , , , , . ( ), , , .
, « » ( , ), . , . , (« » . .). . , - « », , , …
, . , , . , , . , .
, 30 40 , - .
Wolfram Language?
« Wolfram » ( ).