Intégrale d'Euler-Poisson. Détails sur les méthodes de calcul

Dans l'article, en détail, jusqu'au moindre détail, trois méthodes de prise de l'intégrale d'Euler-Poisson sont considérées. Dans l'une des méthodes, une formule de réduction auxiliaire est dérivée. Pour trouver des intégrales complexes, on peut utiliser des formules de réduction qui permettent d'abaisser le degré de l'intégrande et de calculer les intégrales correspondantes en un nombre fini d'étapes.

Cette intégrale est tirée de la fonction gaussienne: $$$I = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx}$
Il existe une méthode mathématique très intéressante. Pour trouver l'intégrale d'origine, recherchez d'abord le carré de cette intégrale, puis prenez la racine du résultat. Pourquoi? Oui, car il est tellement plus facile et indolore d'aller aux coordonnées polaires. Par conséquent, considérons le carré de l'intégrale gaussienne:
$$$I ^ 2 = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} \ int \ limits_0 ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limits_0 ^ \ infty { \ int \ limits_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}}} dxdy$
Nous voyons que nous obtenons une double intégrale d'une fonction $$$g \ left ({x, y} \ right) = \ exp \ left [{- \ left ({x ^ 2 + y ^ 2} \ right)} \ right]$ . À la fin de cette intégrale de surface se trouve l'élément de surface dans le système de coordonnées cartésiennes $$$dS = dxdy$ .
Passons maintenant au système de coordonnées polaires:

$$

$$\ begin {array} {l} dS = dxdy = rd \ varphi \ cdot dr \\ \ left. \ begin {array} {l} x = r \ cos \ varphi \\ y = r \ sin \ varphi \\ \ end {array} \ right | \ à x ^ 2 \ cos ^ 2 \ varphi + y ^ 2 \ sin ^ 2 \ varphi = r ^ 2 \ à x ^ 2 + y ^ 2 = r ^ 2 \\ \ end {array}$$

Il convient de noter ici que r peut varier de 0 à + ∞, car x variait dans la même plage. Mais l'angle φ varie de 0 à π / 2, qui décrivent la région d'intégration dans le premier quart du système de coordonnées cartésiennes. En substituant à la source, on obtient:

$$

$$\ begin {array} {l} I ^ 2 = \ int \ limits_0 ^ \ infty {\ int \ limits_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}} } dxdy = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ int \ limits_0 ^ \ infty {e ^ {- r ^ 2}}} rd \ varphi dr = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} rdr} = \ int \ limits_0 ^ {\ frac {\ pi} {2}} { d \ varphi} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} \ frac {1} {2} d \ left ({r ^ 2} \ right)} = \\ = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({\ left. {- e ^ {- r ^ 2}} \ right | _0 ^ \ infty} \ right) = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({- e ^ {- \ infty} - \ left ({ - e ^ 0} \ right)} \ right) = \ frac {1} {2} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {d \ varphi} = \ frac {1} {2 } \ left ({\ left. \ varphi \ right | _0 ^ {\ frac {\ pi} {2}}} \ right) = \ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ sqrt {\ frac {\ pi} {4}} = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

En raison de la symétrie de l'intégrale et de la plage positive de valeurs de l'intégrande, nous pouvons conclure que

$$

$$\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Trouvons-nous d'autres solutions? C'est intéressant! :)

Considérez la fonction $$$g \ left (t \ right) = \ left ({1 + t} \ right) e ^ {- t}$
Rappelons maintenant les mathématiques de l'école et réalisons une étude simple d'une fonction en utilisant des dérivées et des limites. Ce n'est pas que nous considérerons des limites complexes ici (après tout, ils ne les dépassent pas à l'école), nous discutons simplement de ce qui arrivera à la fonction si son argument tend à zéro ou à l'infini, ainsi nous allons estimer le comportement asymptotique, qui est toujours très important en mathématiques. C'est comme une évaluation qualitative de ce qui se passe.

$$

$$\ begin {array} {l} g \ left (t \ right) = \ left ({1 + t} \ right) e ^ {- t} \\ g '\ left (t \ right) = e ^ { - t} - \ left ({1 + t} \ right) e ^ {- t} = - te ^ {- t} \\ g '\ left (t \ right) = 0 \ to t = 0 \\ \ gauche [\ begin {array} {l} t <0 \ to - te ^ {- t}> 0 \ to g \ left (t \ right) - {\ rm {augmente}} \\ t> 0 \ to - te ^ {- t} <0 \ à g \ gauche (t \ droite) - {\ rm {diminue}} \\ \ end {array} \ droite. \\ g \ left (0 \ right) = \ left ({1 + 0} \ right) e ^ {- 0} = 1 \\ g \ left ({- 1} \ right) = \ left ({1 - 1} \ droite) e ^ {- \ gauche ({- 1} \ droite)} = 0 \\ g \ gauche (\ infty \ droite) = \ gauche ({1 + \ infty} \ droite) e ^ {- \ infty} = 0 \\ \ end {array}$$

Il est délimité ci-dessus par l'unité sur l'intervalle (-∞; + ∞) et zéro sur l'intervalle [-1; + ∞).

Nous effectuons le changement de variables suivant $$$t = \ pm x ^ 2$
Et nous obtenons:

$$

$$t = \ pm x ^ 2 \ to \ left \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) e ^ {x ^ 2} <1 \\ 0 < \ left ({1 + x ^ 2} \ right) e ^ {- x ^ 2} <1 \\ \ end {array} \ right. \ to \ left \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) <e ^ {- x ^ 2} \\ 0 <e ^ {- x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ end {array} \ droite.$$

Dans la première inégalité, nous limitons la variation (0,1) et dans la seconde, l'intervalle (0; + ∞), nous élevons les deux inégalités à la puissance n, car les inégalités avec des termes positifs peuvent être augmentées à n'importe quel degré positif. Nous obtenons:

$$

$$\ begin {array} {* {20} c} {\ left \ {\ begin {array} {l} \ left ({1 - x ^ 2} \ right) ^ n <e ^ {- nx ^ 2} \\ 0 <x <1 \\ \ end {array} \ right.} & {\ Left \ {\ begin {array} {l} e ^ {- nx ^ 2} <\ frac {1} {{\ left ({1 + x ^ 2} \ droite) ^ n}} \\ x> 1 \\ \ end {array} \ droite.} \\ \ end {array}$$

Construisons des graphes pour n = 1 pour démontrer les inégalités

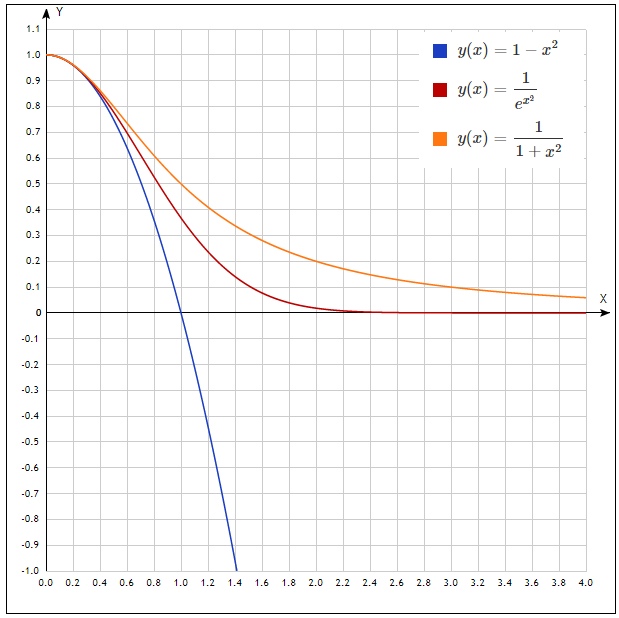
Nous essayons maintenant d'intégrer les inégalités dans les limites indiquées dans les systèmes correspondants. Et combinez immédiatement tout en une seule inégalité:

$$

$$\ int \ limits_0 ^ 1 {\ gauche ({1 - x ^ 2} \ droite) ^ n dx} <\ int \ limits_0 ^ 1 {e ^ {- nx ^ 2} dx} <\ int \ limits_0 ^ \ infty {e ^ {- nx ^ 2} dx} <\ int \ limits_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx}$$

Encore une fois, si vous regardez les graphiques, cette inégalité est vraie.

Étant donné un petit remplacement, il est facile de voir que:

$$

$$\ int \ limits_0 ^ \ infty {e ^ {- nx ^ 2} dx} = \ left [\ begin {array} {l} p = \ sqrt nx \\ p ^ 2 = nx ^ 2 \\ \ frac { {dp}} {{\ sqrt n}} = dx \\ \ end {array} \ right] = \ frac {1} {{\ sqrt n}} \ int \ limits_0 ^ \ infty {e ^ {- p ^ 2} dp} = \ frac {1} {{\ sqrt n}} I$$

C'est-à-dire dans cette grande inégalité au milieu, nous avons l'intégrale d'Euler-Poisson, et maintenant nous devons trouver les intégrales qui se trouvent aux frontières de cette inégalité.

Trouvez l'intégrale à partir de la bordure gauche:

$$

$$\ begin {array} {l} \ int \ limits_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} = \ left [{\ begin {array} {* {20} c} \ begin {array} {l} x = \ sin t \\ dx = \ cos tdt \\ 1 - x ^ 2 = 1 - \ sin ^ 2 t = \ cos ^ 2 t \\ \ end {array} & \ begin {array} {l} x = 1 \ to t = \ arcsin 1 = \ frac {\ pi} {2} \\ x = 0 \ to t = \ arcsin 0 = 0 \\ \ end {array} \\ \ end {array}} \ right] = \\ = \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n} t \ cdot \ cos tdt} = \ int \ limits_0 ^ {{ \ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} \\ \ end {array}$$

Pour le calculer et l'évaluer, trouvons d'abord une intégrale générale. Je vais maintenant vous montrer comment dériver la formule de réduction (en mathématiques, par de telles formules, elles signifient abaisser le degré) pour une intégrale donnée.

$$

$$\ begin {array} {l} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cos tdt} = \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cdot d \ left ({\ sin t} \ right)} = \\ = \ left [{\ begin {array} {* { 20} c} {u = \ cos ^ {n - 1} t} & {du = - \ left ({n - 1} \ right) \ cos ^ {n - 2} t \ sin tdt} \\ {dv = d \ left ({\ sin t} \ right)} & {v = \ sin t} \\ \ end {array}} \ right] = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ droite | _ \ alpha ^ \ beta + \ gauche ({n - 1} \ droite) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ sin ^ 2 tdt} = \\ = \ gauche. {\ cos ^ {n - 1} t \ sin t} \ droite | _ \ alpha ^ \ beta + \ gauche ({n - 1} \ droite) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ gauche ({1 - \ cos ^ 2 t} \ droite) dt} = \\ = \ gauche. {\ cos ^ {n - 1} t \ sin t} \ droite | _ \ alpha ^ \ beta + \ gauche ({n - 1} \ droite) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ end {array}$$

$$

$$\ begin {array} {l} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left. {\ cos ^ {n - 1} t \ sin t} \ droite | _ \ alpha ^ \ beta + \ gauche ({n - 1} \ droite) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt } + \ left ({n - 1} \ right) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left. {\ cos ^ {n - 1} t \ sin t} \ droite | _ \ alpha ^ \ beta + \ gauche ({n - 1} \ droite) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} \\ n \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt = \ left. {\ cos ^ {n - 1} t \ sin t} \ droite | _ \ alpha ^ \ beta + \ gauche ({n - 1} \ droite) \ int \ limits_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt}} \\ \ int \ limits_ \ alpha ^ \ beta {\ cos ^ n tdt = \ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ frac {{n - 1}} {n} \ int \ limits_ \ alpha ^ \ beta {\ cos ^ { n - 2} tdt}} \\ \ end {array}$$

Maintenant, si nous utilisons la formule de réduction, nous considérons la même intégrale, mais avec nos limites de 0 à π / 2, alors nous pouvons faire quelques simplifications:

$$

$$\ begin {array} {l} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ n tdt = \ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 1}} {n} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt}} = \ left [{\ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} = 0} \ right] = \\ = \ frac {{n - 1}} { n} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt} = \ frac {{n - 1}} {n} \ left ({\ frac {1 } {{n - 2}} \ gauche. {\ cos ^ {n - 3} t \ sin t} \ droite | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 3} } {{n - 2}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \\ = \ frac {{n - 1 }} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5 }} {{n - 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 6} tdt}} \ right)} \ right) = \\ = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5}} {{n - 4}} \ left ({\ frac {{n - 7}} {{n - 6}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 8} tdt}} \ right )} \ right)} \ right) = ... \\ \ end {array}$$

Comme nous le voyons, vous pouvez l'abaisser à l'infini (dépend de n). Cependant, il y a une subtilité. La formule change selon que n est un nombre pair ou non.
Pour cela, nous considérons deux cas.

$$

$$\ begin {array} {l} n = 10: \\ \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {10} tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 2 tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ left ({\ frac {1 } {2} + \ frac {1} {2} \ cos 2t} \ right) dt} = \\ = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ gauche. {\ left ({\ frac {1} {2} t + \ frac {1} {2} \ sin 2t} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ cdot \ frac {\ pi} {4} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} {{10 \ cdot 8 \ cdot 6 \ cdot 4 \ cdot 2}} \ cdot \ frac {\ pi} {2} = \\ = \ frac {{\ left ({n - 1} \ à droite) !!}} {{n !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

$$

$$\ begin {array} {l} n = 9: \\ \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 9 tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} \ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} à gauche. {\ left ({\ sint} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \\ = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} { {9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} = \ frac {{\ left ({n - 1} \ right) !!}} {{n !!}} \\ \ end {array}$$

Où est n !! - double factorielle. La double factorielle de n est notée n !! et est défini comme le produit de tous les nombres naturels dans l'intervalle [1, n] ayant la même parité que n

Du fait que 2n + 1 est un nombre impair pour toute valeur de n, nous obtenons pour la frontière gauche de notre inégalité:

$$

$$\ int \ limits_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} = \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ droite) !!}}$$

Trouvez l'intégrale à partir de la bordure droite:
(ici, nous utilisons la même formule de réduction qui a été prouvée précédemment)

$$

$$\ begin {array} {l} \ int \ limits_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx = \ left [\ begin {array } {l} x = \ tan t \ to \ begin {array} {* {20} c} {x = 0 \ to t = 0} \\ {x = \ infty \ to t = \ frac {\ pi} {2}} \\ \ end {array} \\ dx = \ frac {{dt}} {{\ cos ^ 2 t}} \\ \ frac {1} {{1 + x ^ 2}} = \ frac {1} {{1 + \ tan ^ 2 t}} = \ cos ^ 2 t \\ \ end {array} \ right]} = \\ = \ int \ limits_0 ^ {\ frac {\ pi} {2} } {\ cos ^ {2n - 2} tdt} = \ left [{\ left ({2n - 2} \ right) - {\ rm {even}}} right] = \ frac {{\ left ({2n - 3} \ droite) !!}} {{\ gauche ({2n - 2} \ droite) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Après avoir estimé les côtés gauche et droit de l'inégalité, nous effectuons quelques transformations pour évaluer les limites des côtés gauche et droit de l'inégalité, à condition que n tend vers ∞:

$$

$$\ begin {array} {l} \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <\ frac {1} { {\ sqrt n}} \ cdot I <\ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ sqrt n \ cdot \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <I <\ sqrt n \ cdot \ frac {{\ gauche ({2n - 3} \ droite) !!}} {{\ gauche ({2n - 2} \ droite) !!}}} cdot \ frac {\ pi} {2} \\ \ end {array}$$

Carré des deux côtés de l'inégalité:

$$

$$n \ cdot \ frac {{\ gauche ({\ gauche ({2n} \ droite) !!} \ droite) ^ 2}} {{\ gauche ({\ gauche ({2n + 1} \ droite) !! } \ droite) ^ 2}} <I ^ 2 <n \ cdot \ frac {{\ gauche ({\ gauche ({2n - 3} \ droite) !!} \ droite) ^ 2}} {{\ gauche ( {\ gauche ({2n - 2} \ droite) !!} \ droite) ^ 2}} \ cdot \ frac {{\ pi ^ 2}} {4}$$

Faisons maintenant une petite digression. En 1655, John Wallis (un mathématicien anglais, l'un des précurseurs de l'analyse mathématique) a proposé une formule pour déterminer le nombre π. J. Wallis s'approcha d'elle, calculant l'aire d'un cercle. Ce produit converge extrêmement lentement; par conséquent, la formule de Wallis est peu utile pour le calcul pratique du nombre π. Mais c'est génial pour évaluer notre expression :)

$$

$$\ pi = \ mathop {\ lim} \ limits_ {n \ to \ infty} \ frac {1} {n} \ left [{\ frac {{\ left ({2n} \ right) !!}} {{ \ left ({2n - 1} \ right) !!}}} \ right] ^ 2$$

Maintenant, nous transformons nos inégalités afin de voir où substituer la formule de Wallis:

$$

$$\ begin {array} {l} \ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}} \ cdot \ frac {1} {n} \ cdot \ frac { {\ left ({\ left ({2n} \ right) !!} \ right) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2} } <I ^ 2 <\ frac {1} {{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ right) ^ 2 }} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}}} \ cdot \ frac {{\ pi ^ 2}} {4} \\ \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}}} \ right] \ cdot \ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n} \ right) !!} \ right ) ^ 2}} {{\ gauche ({\ gauche ({2n - 1} \ droite) !!} \ droite) ^ 2}}} \ droite] <I ^ 2 <\ frac {1} {{\ mathop {\ lim} \ limits_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ droite) ^ 2}} {{\ gauche ({\ gauche ({2n - 3} \ droite) !!} \ droite) ^ 2}}} \ droite]}} \ cdot \ frac {{\ pi ^ 2} } {4} \\ \ frac {1} {4} \ cdot \ pi <I ^ 2 <\ frac {1} {\ pi} \ cdot \ frac {{\ pi ^ 2}} {4} \ to \ frac {\ pi} {4} <I ^ 2 <\ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Il résulte de la formule de Wallis que les expressions gauche et droite ont tendance à π / 4 comme n → ∞
Étant donné que la fonction exp [-x²] est paire, nous supposons en toute sécurité que

$$

$$\ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Pour la première fois, l'intégrale gaussienne unidimensionnelle a été calculée en 1729 par Euler, puis Poisson a trouvé un moyen simple de la calculer. À cet égard, il a été appelé l'intégrale d'Euler-Poisson.

Essayons de calculer l'intégrale gaussienne. Il peut être écrit sous différentes formes. Après tout, rien ne change le nom de la variable par laquelle l'intégration a lieu.

$$

$$\ begin {array} {l} I = \ int \ limits_0 ^ \ infty {e ^ {- x ^ 2} dx} \\ I = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- y ^ 2} dy} = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- z ^ 2} dz} \\ \ end {array}$$

Vous pouvez passer des coordonnées cartésiennes tridimensionnelles aux coordonnées sphériques et considérer le cube de l'intégrale de Gauss.

$$

$$\ left \ {\ begin {array} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ \ end {tableau} \ droite. \ à x ^ 2 + y ^ 2 + z ^ 2 = r ^ 2$$

Le jacobien de cette transformation peut être calculé comme suit:

$$

$$\ begin {array} {l} J = \ left | {\ begin {array} {* {20} c} {\ frac {{\ partial x}} {{\ partial r}}} & {\ frac {{\ partial x}} {{\ partial \ theta}} } & {\ frac {{\ partial x}} {{\ partial \ varphi}}} \\ {\ frac {{\ partial y}} {{\ partial r}}} & {\ frac {{\ partial y }} {{\ partial \ theta}}} & {\ frac {{\ partial y}} {{\ partial \ varphi}}} \\ {\ frac {{\ partial z}} {{\ partial r}} } & {\ frac {{\ partial z}} {{\ partial \ theta}}} & {\ frac {{\ partial z}} {{\ partial \ varphi}}} \\ \ end {array}} \ à droite | = \ gauche | {\ begin {array} {* {20} c} {\ sin \ theta \ cos \ varphi} & {r \ cos \ theta \ cos \ varphi} & {- r \ sin \ theta \ sin \ varphi} \\ {\ sin \ theta \ sin \ varphi} & {r \ cos \ theta \ sin \ varphi} & {r \ sin \ theta \ cos \ varphi} \\ {r \ cos \ theta} & {- r \ sin \ thêta} & 0 \\ \ end {array}} \ right | = \\ = r ^ 2 \ sin \ theta \\ \ end {array}$$

$$

$$\ begin {array} {l} I ^ 3 = \ int \ limits_ {- \ infty} ^ \ infty {\ int \ limits_ {- \ infty} ^ \ infty {\ int \ limits_ {- \ infty} ^ \ \ infty {e ^ {- x ^ 2 - y ^ 2 - z ^ 2}} dxdydz}} = \ int \ limits_0 ^ {2 \ pi} {\ int \ limits_0 ^ \ pi {\ int \ limits_0 ^ \ infty { e ^ {- r ^ 2} Jdrd \ theta d} \ varphi =}} \\ = \ int \ limits_0 ^ {2 \ pi} {d \ varphi} \ int \ limits_0 ^ \ pi {\ sin \ theta d \ thêta} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} \\ \ end {array}$$

Nous calculons les intégrales séquentiellement, en commençant par l'intérieure.

$$

$$\ begin {array} {l} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} = \ left [\ begin {array} {l} u = r \ to du = dr \\ dv = re ^ {- r ^ 2} dr \ to v = \ int {re ^ {- r ^ 2} dr} = \ frac {1} {2} \ int {e ^ {- r ^ 2} dr ^ 2} = - \ frac {1} {2} e ^ {- r ^ 2} \\ \ end {array} \ right] = \\ = \ left. {\ left ({- \ frac {1} {2} re ^ {- r ^ 2}} \ right)} \ right | _0 ^ \ infty + \ frac {1} {2} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ int \ limits_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ cdot \ frac {I} {2} = \ frac {I} {4} \\ \ int \ limits_0 ^ \ pi {\ sin \ theta d \ theta} = \ left. {\ gauche ({- \ cos \ theta} \ droite)} \ droite | _0 ^ \ pi = \ gauche ({- \ cos \ pi} \ droite) - \ gauche ({- \ cos 0} \ droite) = 1 + 1 = 2 \\ \ int \ limits_0 ^ {2 \ pi} {d \ varphi} = \ left. \ varphi \ right | _0 ^ {2 \ pi} = 2 \ pi \\ \ end {array}$$

Ensuite, nous obtenons:

$$

$$\ begin {array} {l} I ^ 3 = 2 \ pi \ cdot 2 \ cdot \ frac {I} {4} \ to I ^ 3 = \ pi I \ to I ^ 2 = \ pi \ to I = \ sqrt \ pi \\ I = \ int \ limits_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ sqrt \ pi \\ \ end {array}$$

L'intégrale d'Euler-Poisson est souvent utilisée dans la théorie des probabilités.

J'espère que pour quelqu'un l'article sera utile et aidera à comprendre certaines techniques mathématiques :)