Méthodes quasi-newtoniennes ou quand il y a trop de dérivées secondes pour Athos

À la première connaissance des méthodes quasi-newtoniennes, on peut être surpris deux fois. Premièrement, après un rapide coup d'œil aux formules, des doutes surgissent que cela puisse fonctionner. Cependant, ils fonctionnent. De plus, il semble douteux qu'ils fonctionnent bien. Et il est d’autant plus surprenant de voir à quel point elles sont plus rapides que les différentes variations de descente en pente, non pas sur des tâches spécialement construites, mais sur des tâches réelles tirées de la pratique. Et si après cela, il y a encore des doutes mélangés avec de l'intérêt, alors vous devez comprendre pourquoi ce quelque chose fonctionne.

L'origine et les idées de base qui animent les méthodes de gradient, y compris la méthode de Newton, ont déjà été examinées . À savoir, nous nous sommes appuyés sur les informations sur le comportement de la fonction au voisinage de la position actuelle, ce qui nous donne une analyse mathématique simple. À tout le moins, nous avons supposé que nous disposions d'informations sur les premiers dérivés. Et si c'est tout ce dont nous disposons? La descente en gradient est-elle notre phrase? Bien sûr, oui, sauf si vous vous souvenez soudainement que nous avons affaire à un processus dans lequel la fonction objectif est correctement traitée. Et si oui, pourquoi ne pas utiliser les informations accumulées sur le comportement de la fonction pour rendre notre marche à sa surface un peu moins aveugle?

L'idée d'utiliser des informations sur le chemin parcouru est au cœur de la plupart des moyens d'accélérer les méthodes de descente. Cet article présente l'une des méthodes les plus efficaces, mais pas les moins chères, pour rendre compte de ce type d'informations, ce qui a conduit à l'idée de méthodes quasi-newtoniennes.

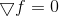
Afin de comprendre où croissent les jambes des méthodes quasi-newtoniennes et d'où vient le nom, nous devons à nouveau revenir à la méthode de minimisation basée sur la solution directe de l'équation ponctuelle stationnaire . Tout comme la prise en compte de la méthode de Newton appliquée à la solution de cette équation nous a conduit à la méthode d'optimisation du même nom (qui, contrairement à son ancêtre, a une région de convergence globale), on peut s'attendre à ce que la considération d'autres méthodes de résolution de systèmes d'équations non linéaires soit fructueuse. planifier des idées pour construire d'autres méthodes d'optimisation.

Méthodes sécantes

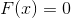
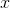
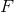
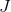
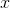
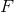
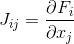
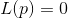
Permettez-moi de vous rappeler que la méthode de Newton pour résoudre le système d'équations , est basé sur le remplacement au voisinage d'un point proche de la solution les fonctions son approximation linéaire où Est un opérateur linéaire qui, lorsqu'il est un vecteur et a des dérivées partielles par rapport à chaque variable, coïncide avec la matrice de Jacobi . 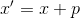Ensuite, l'équation est résolue et pointer comme une nouvelle approximation de la solution souhaitée. C'est simple et ça marche.

Mais que faire si, pour une raison quelconque, nous ne pouvons pas calculer la matrice de Jacobi? La première chose qui vient à l'esprit dans ce cas est que si nous ne pouvons pas calculer analytiquement les dérivées partielles, alors nous pouvons bien obtenir une approximation numérique pour elles. 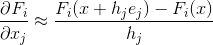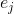L'option la plus simple (bien que nullement la seule) pour une telle approximation peut être la formule des différences finies droites: où Est le jème vecteur de base. La matrice composée de telles approximations sera désignée par . 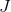Une analyse de la quantité de remplacement sur dans la méthode de Newton, sa convergence affecte, un assez grand nombre d'ouvrages sont consacrés, mais dans ce cas nous nous intéressons à un autre aspect. 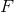A savoir, une telle approximation nécessite le calcul de la fonction en N points supplémentaires, et, en outre, la fonction à ces points interpole la fonction , c'est-à-dire



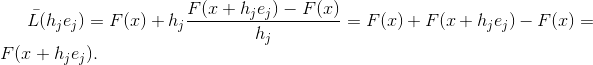
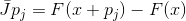
Toutes les approximations de la matrice de Jacobi n'ont pas cette propriété, mais chaque matrice d'une fonction affine qui a cette propriété est une approximation de la matrice de Jacobi. En effet, si et puis à . Cette propriété, à savoir la propriété d'interpolation, nous donne un moyen constructif de généraliser la méthode de Newton.

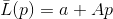
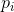
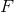
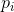
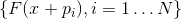
Soit - fonction satisfaisant à l'exigence pour un système de vecteurs linéairement indépendants . Ensuite, une telle fonction est appelée fonction sécante et l'équation qui le définit est l'équation sécante . 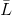Si le système de vecteurs est complet (c'est-à-dire qu'il y en a exactement N et qu'ils sont toujours linéairement indépendants), et, en plus, le système de vecteurs linéairement indépendant alors défini de façon unique.

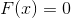
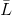
Toute méthode basée sur un changement local d'équation équation de la forme où satisfait l'équation sécante , appelée la méthode sécante .

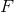
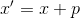
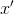
Une bonne question se pose de savoir comment construire la sécante d'une fonction de la manière la plus rationnelle. . Le raisonnement suivant semble évident: laissez un modèle affine être construit au point x qui interpole la fonction donnée aux points . Solution d'équation nous donne un nouveau point . 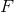Ensuite, pour construire un modèle affine à un point il est plus raisonnable de choisir des points d'interpolation pour que la valeur déjà connu - c'est-à-dire, prenez-les de l'ensemble . 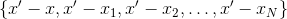Il existe différentes options pour choisir les points parmi les nombreux précédemment utilisés. 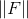Par exemple, vous pouvez prendre comme points d'interpolation ceux dans lesquels importe le moins ou juste le premier des points. En tout cas, il semble évident que devrait être inclus dans de nombreux points d'interpolation pour le nouveau modèle affine. 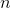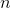Au-delà les étapes du processus itératif dans notre ensemble peuvent aller jusqu'à déplacements construits sur des points précédemment passés. 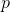Si le processus est construit de telle manière que le nouveau modèle affine n'utilise plus des valeurs précédentes, alors un tel processus est appelé la méthode sécante de p-point.

À première vue, il peut sembler que la méthode sécante à N points est la meilleure candidate pour remplacer la méthode de Newton, car elle utilise au maximum les informations que nous obtenons dans le processus de résolution, tout en minimisant le nombre de calculs supplémentaires - nous utilisons la valeur de la fonction dans cette dernière N points passés. Ce n'est malheureusement pas le cas. 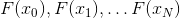Le fait est que le système vectoriel refuse obstinément d'être indépendant linéairement avec un N. suffisamment grand. De plus, même si cette condition s'avère être remplie et que le modèle affine correspondant existe toujours, alors il y a une chance que les directions s'avèrent également linéairement indépendants, il s'avère encore moins. Et cela implique le fait que le modèle affine, bien qu'il existe, est dégénéré et pratiquement inadapté.

En général, la plus stable est la méthode sécante à 2 points. Autrement dit, une méthode dans laquelle, à chaque itération, nous devons calculer des valeurs N-1 supplémentaires de la fonction. Cela ne convient manifestement pas à nos fins pratiques.

Alors la question est - qu'est-ce que tout cela?

Méthodes quasi-newtoniennes pour résoudre des équations

La sortie est simple, mais pas évidente. Si nous n'avons pas la capacité technique, sur la base des valeurs déjà calculées, de déterminer de manière unique le modèle affine qui satisfait l'équation sécante, alors ce n'est pas nécessaire. Nous prenons l'équation des sécantes comme base, mais nous exigerons qu'elle ne soit satisfaite que pour un système incomplet de vecteurs . En d'autres termes, nous exigerons que la condition d'interpolation ne soit satisfaite que pour un nombre suffisamment petit de valeurs connues. Bien sûr, dans ce cas, nous ne pouvons plus garantir que la matrice utilisée dans un tel modèle tendra vers la matrice de Jacobi, mais nous n'en aurons pas besoin. De plus, le modèle affine doit interpoler la fonction au point courant, c'est-à-dire , nous obtenons la formulation suivante de la méthode sécante:



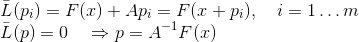
Bruiden a été le premier à envisager des méthodes de ce type pour m = 1, les qualifiant de quasi-newtoniennes. Il est clair que la condition sécante dans ce cas nous permet d'identifier de manière unique la matrice seulement si des conditions supplémentaires lui sont imposées, et chacune de ces conditions supplémentaires donne lieu à une méthode distincte. Bruyden lui-même a raisonné comme suit:

comme le mouvement dans le sens du point 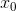au point ne nous donne aucune information supplémentaire sur la façon dont la fonction change 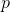directions, puis l'effet de la nouvelle fonction affine sur le vecteur devrait différer de l'effet de l'ancienne fonction sur le même vecteur moins le plus différent de 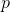. En dernier recours, lorsque orthogonale 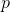, le comportement de la nouvelle fonction ne doit pas être différent de celui de l'ancienne.

L'idée de Breiden est brillante dans sa simplicité. En effet, si nous ne disposons pas de nouvelles informations sur le comportement de la fonction, le mieux que nous puissions faire est d'essayer de ne pas encrasser l'ancienne. Ensuite, la condition supplémentaire

pour tous tel que

vous permet de déterminer de manière unique la matrice de la nouvelle transformation - elle est obtenue en ajoutant une correction de rang 1 à l'ancienne matrice.



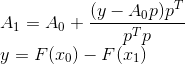
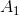
Cependant, malgré la simplicité et la cohérence des conclusions de Bruiden, elles ne fournissent pas le point d'appui qui pourrait servir de base à la construction d'autres méthodes similaires. Heureusement, il existe une expression plus formelle de son idée. À savoir, la matrice construite de cette façon Il s'avère être la solution au problème suivant:



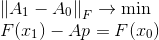
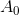
La contrainte de tâche n'est rien d'autre que l'équation sécante, et la condition de minimisation reflète notre désir de sauvegarder autant d'informations que possible dans la matrice . La mesure de l'écart entre les matrices dans ce cas est la norme Frobenius, dans laquelle le problème posé a une solution non ambiguë. Cette formulation pourrait bien servir de point de départ à la construction d'autres méthodes. À savoir, nous pouvons changer à la fois la mesure par laquelle nous évaluons les changements introduits et resserrer les conditions imposées à la matrice. En général, on peut déjà travailler avec une telle formulation de la méthode.

Méthodes d'optimisation Quasi-Newton

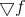
Ayant compris l'idée principale, nous pouvons enfin revenir à des problèmes d'optimisation et remarquer que l'application de la formule de Bruyden pour recalculer le modèle affine ne correspond pas très bien à notre tâche. En fait, la première dérivée de la fonction de gradient il n'y a rien d'autre que la matrice de Hesse, qui par construction est symétrique. 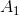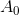Dans le même temps, la mise à jour selon la règle de Bruyden conduit à une matrice asymétrique même si était symétrique. Cela ne signifie pas que la méthode de Bruden ne peut pas être appliquée pour résoudre l'équation ponctuelle stationnaire, mais sur la base d'une telle règle de mise à jour, il est peu probable que nous puissions construire de bonnes méthodes d'optimisation. En général, il est assez évident que la méthode quasi-Newton devrait fonctionner mieux, plus le système de conditions du problème décrit avec précision les spécificités d'une matrice Jacobi spécifique.

Pour corriger cet inconvénient, nous ajoutons une contrainte supplémentaire au problème de minimisation de Bruden, exigeant explicitement que la nouvelle matrice soit symétrique avec l'ancienne:



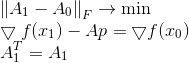
La solution à ce problème est



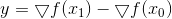
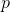
Ici et la formule de recalcul de la matrice porte le nom de ses créateurs - Powell, Shanno et Bruyden (PSB). La matrice résultante est symétrique, mais clairement pas définie positive, ne serait-ce que soudainement ne sera pas colinéaire . Et nous avons vu qu'une certitude positive est hautement souhaitable dans les méthodes d'optimisation.

Encore une fois, nous corrigerons l'état du problème, en utilisant cette fois la norme de Frobenius mise à l'échelle comme mesure de la divergence matricielle.



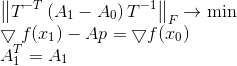
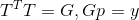
L'origine d'un tel énoncé de la question est un grand sujet distinct, mais il est intéressant de noter que si la matrice T est telle que (c'est-à-dire que G est également une matrice de transformation affine satisfaisant l'équation sécante pour la direction p), alors la solution à ce problème se révèle être indépendante du choix de T et conduit à la formule de mise à jour



connue sous le nom de formule Davidon-Fletcher-Powell. Cette méthode de mise à jour a fait ses preuves dans la pratique, car elle a la propriété suivante:

si et 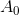positif défini alors 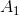également identifiées positivement.

Je note ensuite que si la première condition n'est pas remplie, alors il n'existe pas de fonction affine avec une matrice définie positive qui satisfasse l'équation sécante.

Si dans le problème conduisant à la méthode DFP, on prend, comme mesure de la divergence des modèles affines, la distance non pas entre les matrices elles-mêmes, mais entre les matrices inverses, on obtient un problème de forme



Sa solution est une formule bien connue, découverte presque simultanément par Breiden, Fletcher, Goldfarb et Shanno (BFGS).



À ce jour, on pense que le recalcul selon cette formule est le plus efficace d'un point de vue informatique et en même temps moins sujet à la dégénérescence de la matrice avec un grand nombre d'itérations. Dans les mêmes conditions que DFP, cette formule conserve la propriété du caractère définitif positif.

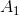
Toutes les méthodes décrites pour la mise à jour de la matrice nécessitent une correction de rang 2. Cela permet d'inverser facilement et facilement la matrice en utilisant la formule Sherman-Morrison et la valeur .



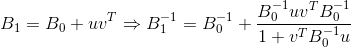
à condition que le dénominateur de la formule soit non nul. Je ne donnerai pas de formules spécifiques pour mettre à jour les matrices inverses des méthodes listées, car elles sont faciles à trouver ou à dériver indépendamment. La seule chose à noter dans ce cas est que les variantes des méthodes de mise à jour de la matrice inverse sont généralement beaucoup moins stables (c'est-à-dire qu'elles souffrent davantage d'erreurs d'arrondi) que celles qui suggèrent de mettre à jour la matrice d'origine. Il est plus efficace de mettre à jour non pas la matrice elle-même, mais sa décomposition Cholesky (à moins, bien sûr, qu'une telle décomposition ait lieu), car une telle option de mise en œuvre est plus stable numériquement et, en outre, minimise le coût de résolution d'une équation qui détermine la direction du mouvement.

Il reste à examiner la question de savoir à quoi devrait ressembler la toute première matrice dans le processus quasi-newtonien. Tout est évident ici - plus elle est proche de la matrice de Hesse ou de sa version corrigée, si la Hesse ne se révèle pas soudainement définie positive, mieux ce sera du point de vue de la convergence. Cependant, en principe, toute matrice définie positive peut nous convenir. La version la plus simple d'une telle matrice est une seule, puis la première itération coïncide avec l'itération de la descente de gradient. Fletcher et Powell ont montré (naturellement, pour la méthode DFP) que si la fonction quadratique est minimisée, quelle que soit la matrice (définie positive) utilisée comme itération DFP initiale, elles conduiront à une solution dans exactement N itérations, où N est dimension du problème, et la matrice quasi-newtonienne coïncide avec la matrice de Hesse au point minimum. Dans le cas général non linéaire d'un tel bonheur, nous n'attendrons bien sûr pas, mais cela donne au moins des raisons de ne pas trop se soucier du mauvais choix de la matrice initiale.

Conclusion

L'approche décrite de la construction de méthodes quasi-newtoniennes n'est pas la seule possible. Au minimum, les découvreurs des méthodes quasi-newtoniennes décrites et de nombreux chercheurs ultérieurs sont arrivés aux mêmes formules basées sur des considérations complètement différentes. Cependant, il est intéressant de noter que dès qu'une certaine méthode quasi-newtonienne est apparue, quelle que soit la méthode d'obtention, après un temps assez court, il est devenu clair qu'il s'agissait d'une solution à un problème d'optimisation très facilement interprétable. À mon avis, il est remarquable qu'il soit possible d'apporter un dénominateur commun pour des méthodes aussi diverses, car cela fournit la base pour construire d'autres méthodes qui prennent mieux en compte les spécificités d'une tâche particulière. En particulier, il existe des méthodes quasi-Newton conçues pour mettre à jour des matrices clairsemées, des méthodes dans lesquelles le plus petit nombre possible d'éléments subissent des modifications, et bien d'autres seraient un fantasme.

Il convient également de noter que les méthodes de métriques variables, malgré leur nom, ne conduisent pas toujours à la construction de matrices, qui sont en fait des métriques, bien qu'elles le fassent chaque fois que cela est possible. , , — , - . , , . , . , — .

, . , ( , , N , , ). ( , , ), . , , — . — .