Le thème des Allocators apparaît souvent sur Internet: en effet, un Allocator est une sorte de pierre angulaire, le cœur de toute application. Dans cette série d'articles, je veux parler en détail d'un allocateur très divertissant et éminent -
JeMalloc , soutenu et développé par Facebook et utilisé, par exemple, dans
bionic [Android] lib C.Je n'ai pas pu trouver de détails sur le réseau qui révèlent pleinement l'âme de cet allocateur, ce qui a finalement affecté l'impossibilité de tirer des conclusions sur l'applicabilité de JeMalloc dans la résolution d'un problème particulier. Beaucoup de matériel est sorti et, pour lire ce n'était pas fatigant, je propose de commencer par les bases: Structures de données de base utilisées dans JeMalloc.
Sous le chat, je parle de
Pairing Heap et
Bitmap Tree , qui forment la base de JeMalloc. À ce stade, je n'aborde pas le sujet du
multithreading et du
verrouillage à grain fin , mais en poursuivant la série de messages, je vais certainement vous parler de ces choses, pour le plaisir, en fait, différents types d'exotiques sont créés, en particulier celui décrit ci-dessous.
Bitmap_s est une structure de données arborescente qui vous permet de:
- Trouvez rapidement le premier bit activé / désactivé dans une séquence de bits donnée.
- Modifiez et obtenez la valeur d'un bit d'index i dans une séquence de bits donnée.
- L'arbre est construit selon une séquence de n bits et a les propriétés suivantes:
- L'unité de base de l'arbre est le nœud, et l'unité de base du nœud est le bit. Chaque nœud se compose exactement de k bits. Le nombre de bits d'un nœud est sélectionné de sorte que les opérations logiques sur une plage sélectionnée de bits soient calculées aussi rapidement et efficacement que possible sur un ordinateur donné. Dans JeMalloc, un nœud est représenté par un type long non signé .
- La hauteur de l'arbre est mesurée en niveaux et pour une séquence de n bits est H = niveaux.
- Chaque niveau de l'arbre est représenté par une séquence de nœuds, ce qui équivaut à une séquence de peu.
- Le niveau le plus élevé (racine) de l'arborescence est composé de k bits et le plus bas - de n bits.
- Chaque bit d'un nœud de niveau L détermine l'état de tous les bits d'un nœud enfant de niveau L - 1: si un bit est défini sur occupé, alors tous les bits d'un nœud enfant sont également définis sur occupés, sinon, les bits d'un nœud enfant peuvent avoir état «occupé» et «libre».
Il est raisonnable de représenter bitmap_t dans deux tableaux: le premier, d'une dimension égale au nombre de tous les nœuds d'arbre - pour stocker les nœuds d'arbre, et le second, de la dimension de hauteur d'arbre - pour stocker le décalage du début de chaque niveau dans le tableau de nœuds d'arbre. Avec cette méthode de spécification d'un arbre, l'élément racine peut aller d'abord, puis, en séquence, les nœuds de chacun des niveaux. Cependant, les auteurs de JeMalloc stockent l'élément racine en dernier dans le tableau, et devant lui se trouvent les nœuds des niveaux d'arborescence sous-jacents.
À titre d'exemple illustratif, prenez une séquence de 92 bits et K = 32 esprit. Nous supposons que l'état est «libre» - désigné par un seul bit, et l'état «occupé» - zéro. Supposons également que dans la séquence de bits d'origine, le bit d'index 1 (comptage à partir de zéro, de droite à gauche sur la figure) est mis à l'état occupé. Ensuite, bitmap_t pour une telle séquence de bits ressemblera à l'image ci-dessous:
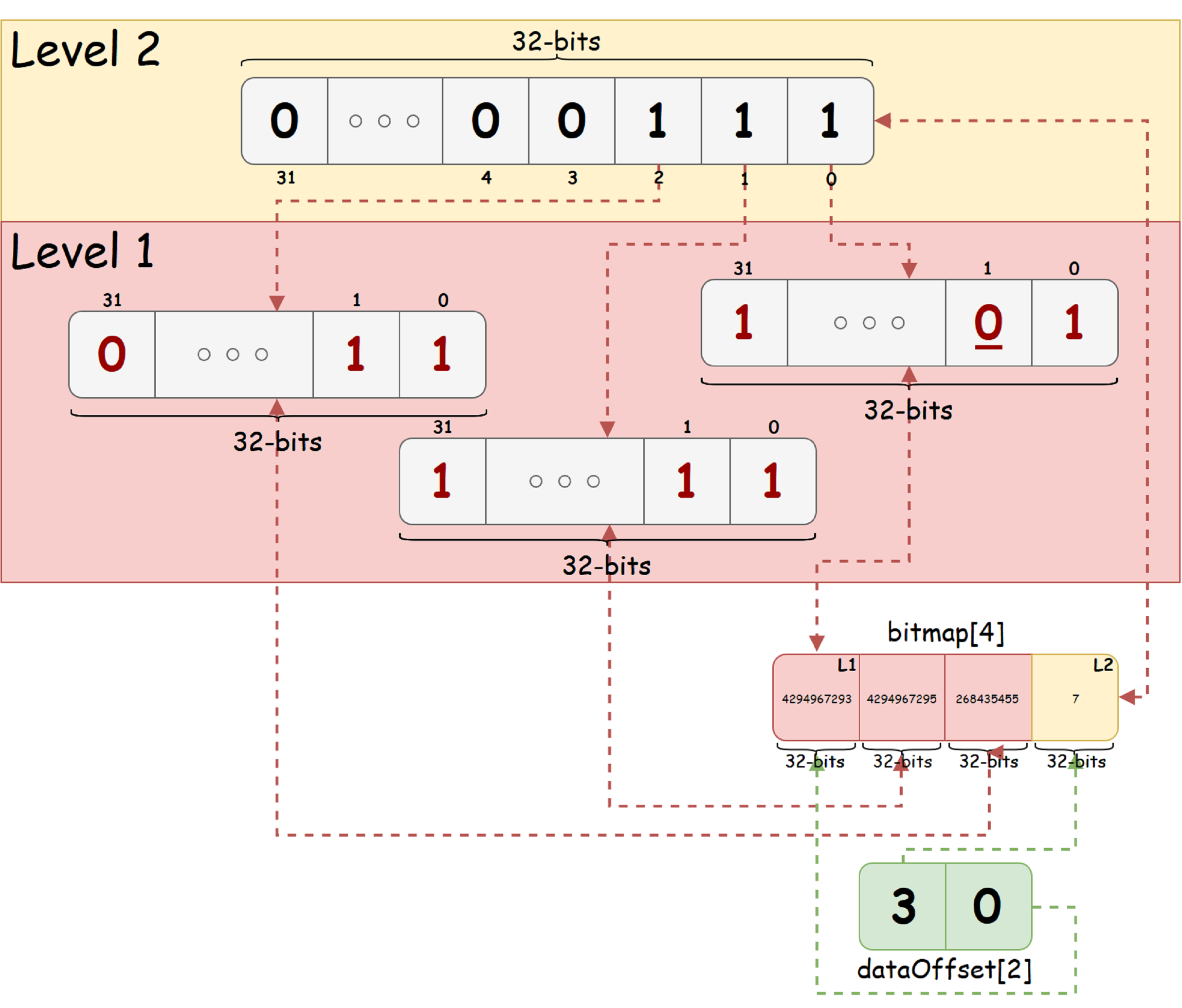Sur la figure, nous voyons que l'arbre résultant n'a que deux niveaux. Le niveau racine contient 3 bits unitaires, ce qui indique la présence de bits libres et occupés dans chacun des nœuds enfants du bit correspondant. Dans le coin inférieur droit, vous pouvez voir l'arborescence dans deux tableaux: tous les nœuds d'arbre et les décalages de chaque niveau dans le tableau de nœuds.En supposant que bitmap_t est représenté par deux tableaux (un tableau de données et un tableau de décalages au niveau de l'arborescence dans le tableau de données), nous décrivons l'opération de recherche du premier bit le moins significatif dans un bitmap_t donné:
- À partir du nœud racine, nous effectuons l'opération de recherche pour le premier bit le moins significatif du nœud: pour résoudre ce problème, les processeurs modernes fournissent des instructions spéciales qui peuvent réduire considérablement le temps de recherche. Nous enregistrerons le résultat trouvé dans la variable FirstSetedBit .
- A chaque itération de l'algorithme, nous conserverons la somme des positions des bits trouvés: countOfSettedBits + = FirstSetedBit
- En utilisant le résultat de l'étape précédente, nous allons au nœud enfant du premier bit unitaire le moins significatif du nœud et répétons l'étape précédente. La transition s'effectue selon la formule simple suivante:
- Le processus se poursuit jusqu'à ce que le niveau le plus bas de l'arbre soit atteint. countOfSettedBits - le numéro du bit souhaité dans la séquence de bits d'entrée.
Pairing Heap est une structure de données arborescente de type tas qui vous permet de:
- Insérez un élément avec une complexité temporelle constante de O (1) et un coût amorti de O (log N) ou O (1) , selon l'implémentation.
- Recherche au moins pour un temps constant - O (1)
- Fusionner deux tas de couplage avec une complexité temporelle constante - O (1) et un coût amorti O (log N) ou O (1) - selon la mise en œuvre
- Supprimer un élément arbitraire (en particulier un élément minimal) avec une estimation de complexité temporaire en O (N) et une estimation de complexité amortie en O (log N)
Plus formellement, Pairing Heap est un arbre arbitraire avec une racine dédiée qui satisfait les propriétés du tas (la clé de chaque sommet n'est ni plus ni moins que la clé de son parent).
Un tas de couplage typique dans lequel la valeur du nœud enfant est inférieure à la valeur du nœud parent (aka Min Pairing Heap) ressemble à ceci:
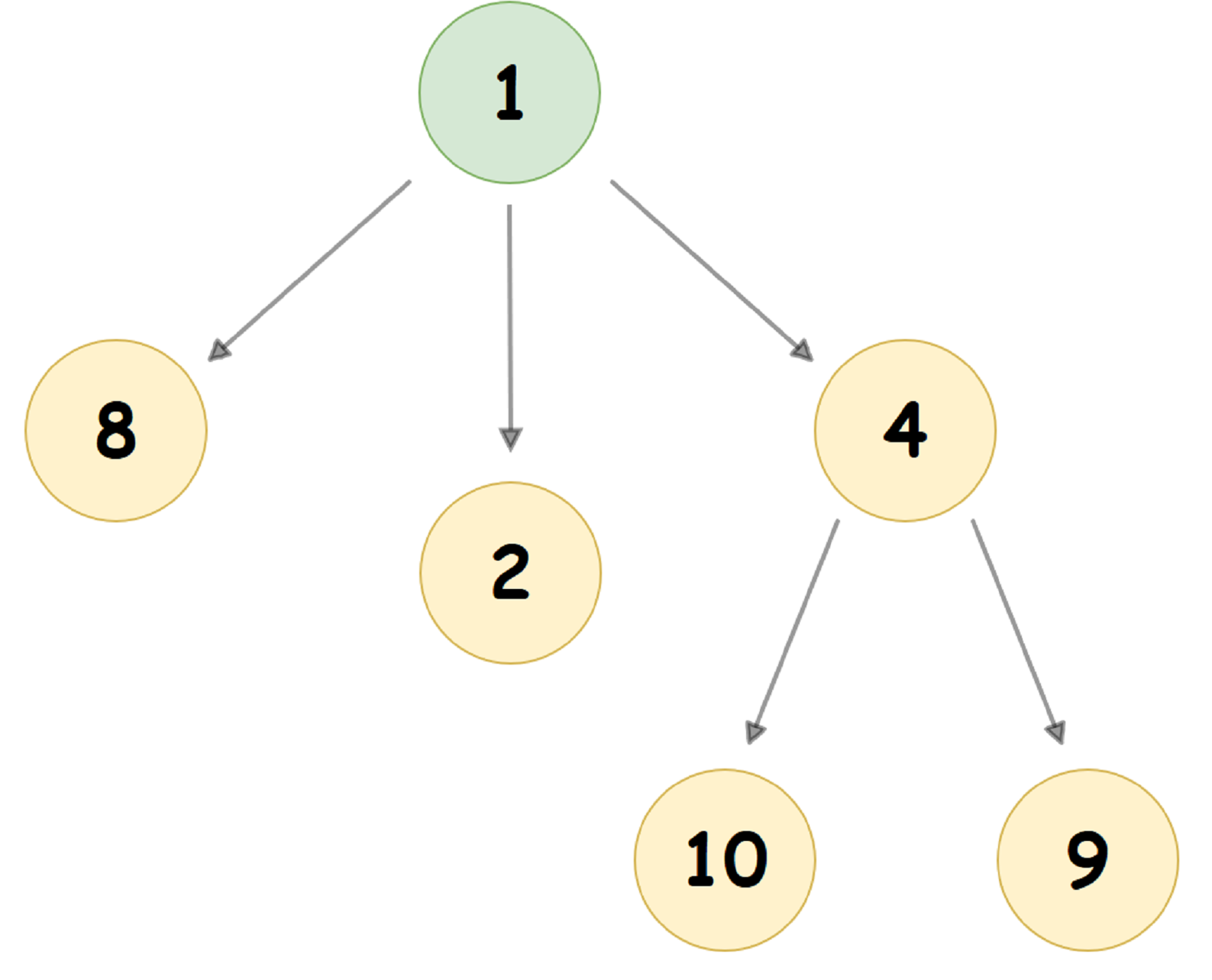
Dans la mémoire de l'ordinateur, Pairing-Heap, en règle générale, est présenté d'une manière complètement différente: chaque nœud de l'Arbre stocke 3 pointeurs:
- Pointeur vers le nœud enfant le plus à gauche du nœud actuel
- Pointeur vers le frère gauche du nœud
- Pointeur vers le frère droit du nœud
Si l'un des nœuds indiqués est manquant, le pointeur de nœud correspondant est annulé.
Pour le tas présenté dans la figure ci-dessus, nous obtenons la représentation suivante:
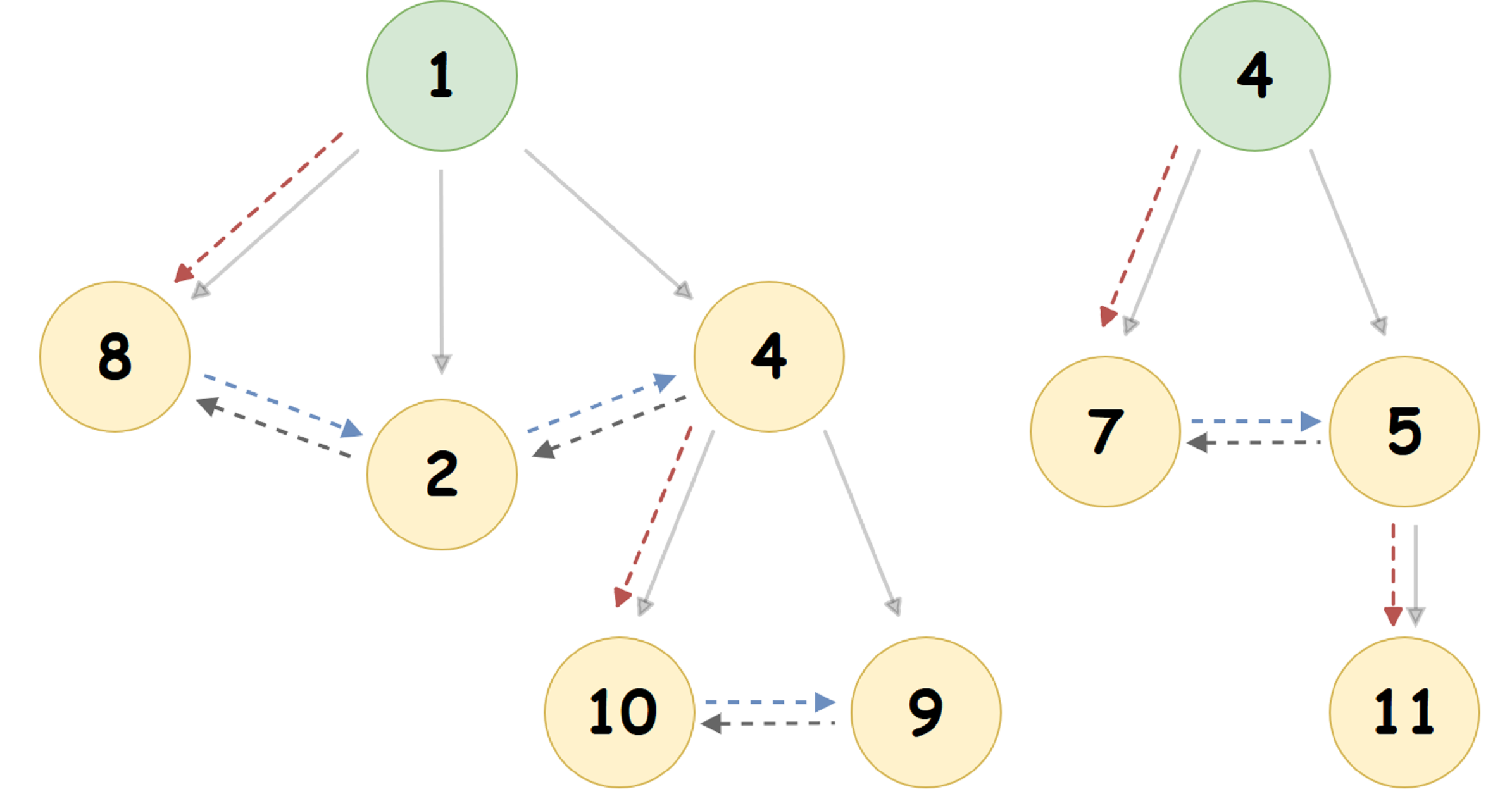Ici, le pointeur vers le nœud enfant le plus à gauche est indiqué par une flèche pointillée rouge, le pointeur vers le frère droit du nœud est bleu et le pointeur vers le frère gauche est gris. La flèche pleine montre la représentation du tas de couplage sous une forme arborescente courante pour une personne.Veuillez noter les deux faits suivants:
- À la racine du tas, il n'y a toujours pas de frères droit et gauche.
- Si un nœud U a un pointeur non nul vers le nœud enfant le plus à gauche, alors ce nœud sera la «tête» de la liste doublement liée de tous les nœuds enfants de U. Cette liste est appelée siblingList.
Ensuite, nous listons l'algorithme des opérations principales dans le
tas d'appariement min :
- Insérez le nœud dans le tas de couplage:
Soit donné un tas de couplage avec une racine et une valeur dedans {R, V_1} , ainsi qu'un nœud {U, V_2} . Ensuite, lors de l'insertion d'un nœud U dans un segment de couplage donné:
- Si la condition V_2 <V_1 est satisfaite: U devient le nouveau nœud racine du tas, "évincant" la racine R à la position de son nœud enfant gauche. En même temps, le frère droit du nœud R devient son nœud le plus à gauche le plus ancien, et le pointeur vers le nœud le plus à gauche du nœud R devient zéro.
- Sinon: U devient le nœud enfant le plus à gauche de la racine de R, et son frère aîné est le nœud le plus à gauche de la racine de R.
- Fusion de deux segments de couplage:
Soit deux segments d'appariement avec des racines et des valeurs en eux {R_1, V_1} , {R_2, V_2}, respectivement, donnés. Nous décrivons l'un des algorithmes de fusion de ces tas dans le tas de couplage résultant:
- Choisissez le tas avec la valeur la plus basse à la racine. Que ce soit un groupe de {R_1, V_1}.
- 'Détachez' la racine R_1 du tas sélectionné: pour cela, nous annulons simplement son pointeur sur le nœud enfant le plus à gauche.
- Avec le nouveau pointeur sur le nœud enfant le plus à gauche de la racine R_1, créez la racine R_2. Notez qu'à partir de maintenant, R_2 perd le statut racine et est un nœud normal dans le tas résultant.
- Nous définissons le frère droit du nœud R_2: avec la nouvelle valeur, nous créons l'ancien pointeur (avant la mise à zéro) sur le nœud enfant le plus à gauche de la racine R_1, et pour R_1, respectivement, mettons à jour le pointeur sur le frère gauche.
Considérez l'algorithme de fusion à l'aide d'un exemple spécifique:
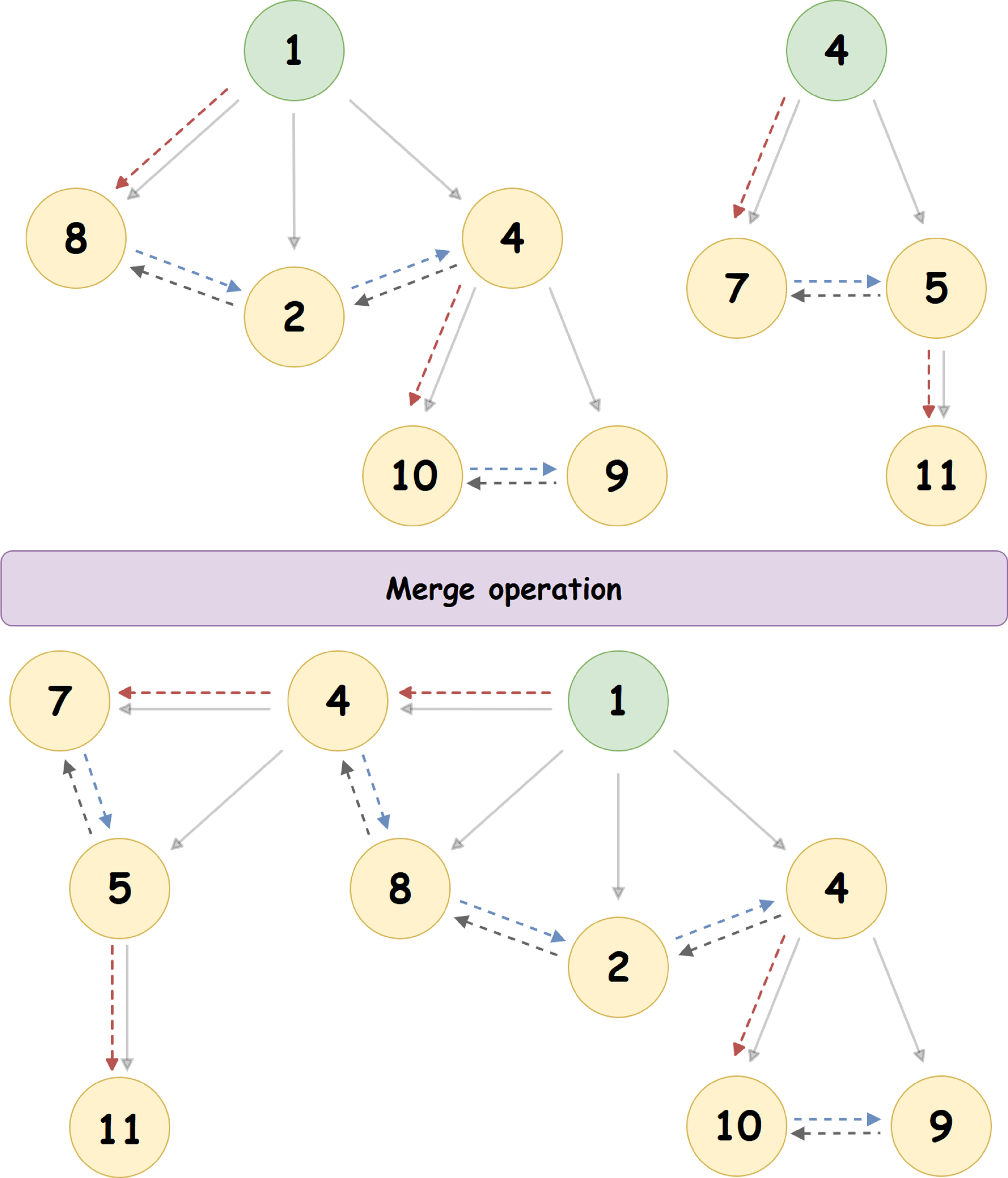Ici, le tas avec la racine «4» rejoint le tas avec la racine «1» (1 <4), devenant son nœud enfant le plus à gauche. Le pointeur vers le frère droit du nœud '4' - est mis à jour, ainsi que le pointeur vers le frère gauche du nœud '8'.- Suppression de la racine (nœud avec la valeur minimale) Pairing Heap:
Il existe plusieurs algorithmes pour supprimer un nœud d'un tas de couplage, garantissant une estimation amortie de la complexité en O (log N). Nous en décrivons un, appelé algorithme multipasse et utilisé dans JeMalloc:
- Nous supprimons la racine du tas donné, ne laissant que son nœud enfant le plus à gauche.
- Le nœud enfant le plus à gauche forme une liste doublement liée de tous les nœuds enfants du nœud parent et, dans notre cas, la racine précédemment supprimée. Nous allons parcourir cette liste de manière séquentielle jusqu'à la fin et, en considérant les nœuds comme les racines du tas de couplage indépendant, effectuer l'opération de fusion de l'élément actuel de la liste avec le suivant, en plaçant le résultat dans une file d'attente FIFO pré-préparée.
- Maintenant que la file d'attente FIFO est initialisée, nous allons itérer dessus, effectuant l'opération de fusion de l'élément actuel de la file d'attente avec le suivant. Le résultat de la fusion est placé à la fin de la file d'attente.
- Nous répétons l'étape précédente jusqu'à ce qu'un élément reste dans la file d'attente: le tas de couplage résultant.
Un bon exemple du processus décrit ci-dessus:
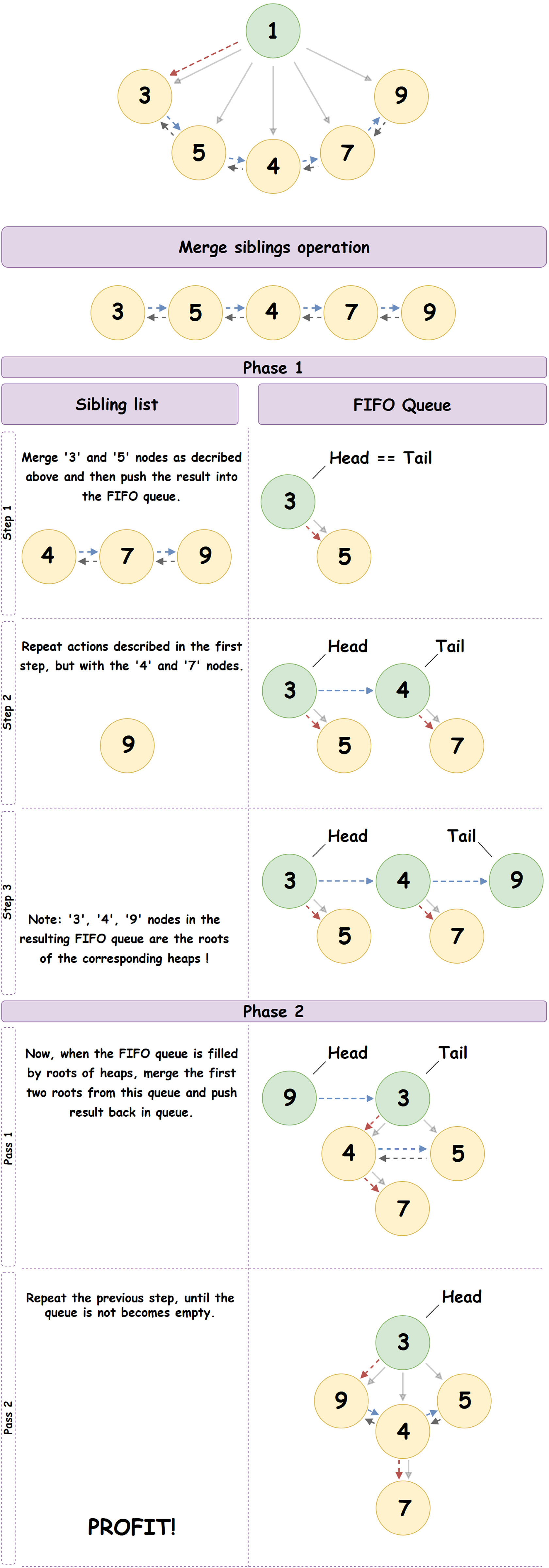
- Suppression d'un tas de couplage de nœuds non root arbitraire:
Considérez le nœud supprimé comme la racine de certains sous-arbres du tas d'origine. Tout d'abord, nous supprimons la racine de cette sous-arborescence, en suivant l'algorithme décrit précédemment pour supprimer la racine du tas de couplage, puis nous exécutons la procédure de fusion de l'arborescence résultante avec l'arborescence d'origine. - Obtention de l'élément de segment de couplage minimum:
Renvoyez simplement la valeur de la racine du tas.
Cependant, notre connaissance de Pairing Heap ne s'arrête pas là: Pairing Heap vous permet d'effectuer certaines opérations non pas immédiatement, mais uniquement en cas de besoin. En d'autres termes, Pairing Heap vous permet d'effectuer des opérations
«paresseusement» , réduisant ainsi le coût amorti de certaines d'entre elles.
Supposons que nous ayons fait K insertions et K suppressions dans Pairing Heap. De toute évidence, le résultat de ces opérations ne devient nécessaire que lorsque nous demandons l'élément minimum du tas.
Voyons comment l'algorithme des actions des opérations décrites précédemment changera au cours de leur implémentation Lazy:
Profitant du fait que la racine de Kuchi a au moins deux pointeurs nuls, nous utiliserons l'un d'entre eux pour représenter la tête d'une liste doublement liée (ci-après
auxList ) d'éléments insérés dans le tas, chacun étant considéré comme la racine d'un tas de couplage indépendant. Ensuite:
- Insertion de nœud paresseux dans le tas de couplage:
Lors de l'insertion du nœud U spécifié dans le tas de couplage { R_1 , V_1 }, nous le mettons dans auxList - après le début de la liste:
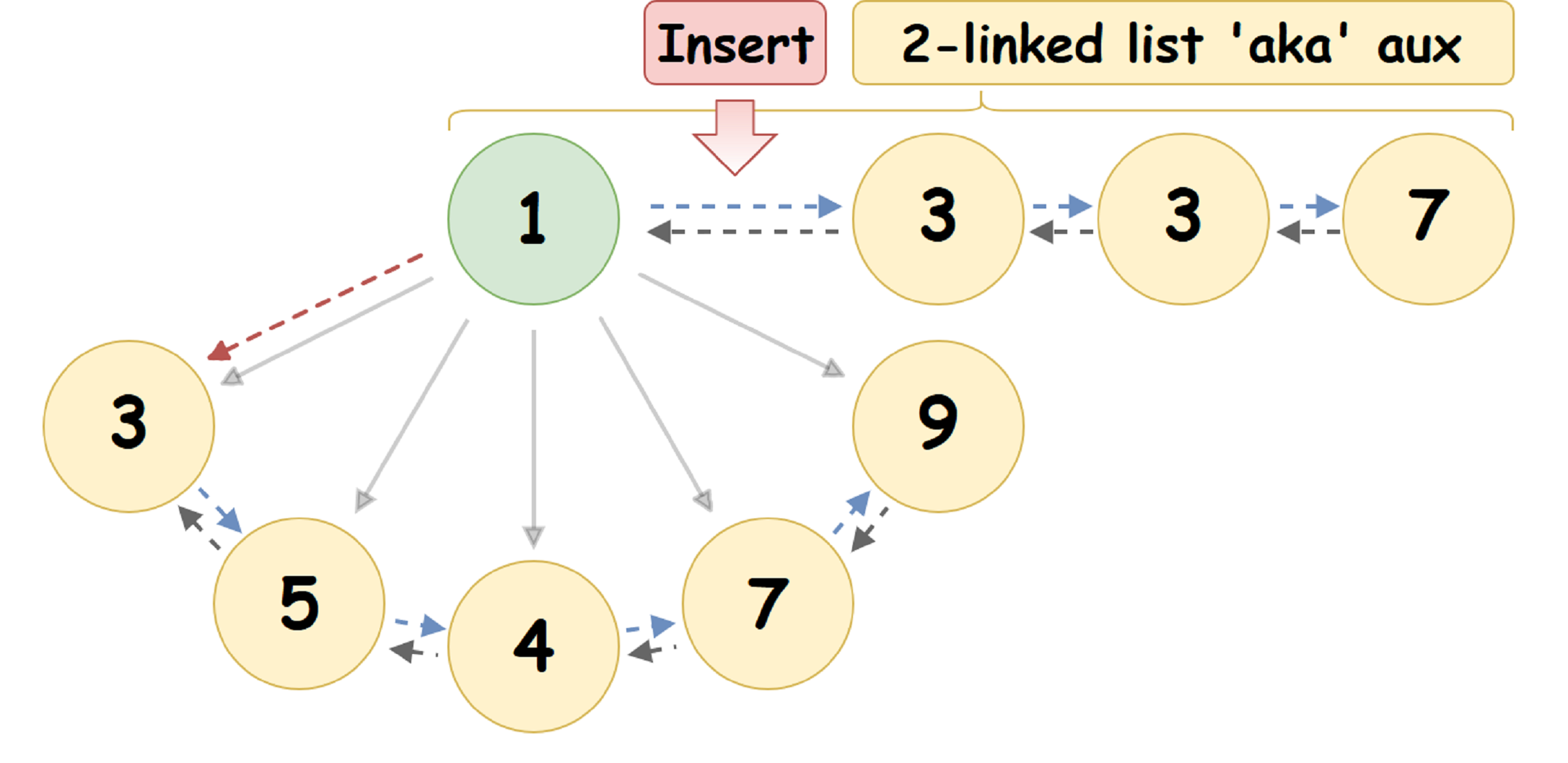
- La fusion paresseuse de deux paires de paires:
Lazy Merging two Pairing Heap, similaire à l'insertion de nœud Lazy, où le nœud inséré est la racine (tête de l'auxList doublement connectée) de l'un des tas. - Lazy obtient l'élément de tas de couplage minimum:
Lorsque vous demandez un minimum, nous passons par auxList à la liste des racines du tas de couplage indépendant, en combinant par paire les éléments de cette liste avec l'opération de fusion, et renvoyons la valeur de la racine contenant l'élément minimum à l'un des tas de couplage résultants. - Suppression paresseuse de l'élément de segment de couplage minimum:
Lorsque vous demandez la suppression de l'élément minimum spécifié par le tas de couplage, nous trouvons d'abord le nœud contenant l'élément minimum, puis le supprimons de l'arborescence dans laquelle il est la racine, en insérant ses sous-arbres dans la liste auxiliaire du tas principal. - Suppression paresseuse d'un nœud de tas de couplage non root arbitraire:
Lors de la suppression d'un nœud de segment de couplage non root arbitraire, le nœud est supprimé du segment de mémoire et ses nœuds enfants sont insérés dans la liste AuxList du segment de mémoire principal.
En fait, l'utilisation de l'implémentation du tas de couplage paresseux réduit le coût amorti de l'insertion et de la suppression de nœuds arbitraires dans le tas de couplage: de O (log N) à O (1).
C’est tout et vous trouverez ci-dessous une liste de liens et de ressources utiles:
[0] Page Github JeMalloc[1] Article original sur le jumelage des tas[2] Article original sur les tas d'association d'implémentations paresseuses[3] Canal télégramme sur les optimisations de code, C ++, Asm, «bas niveau» et rien de plus!À suivre ...