Équation de Navier-Stokes et simulation des fluides sur CUDA

Salut, Habr. Dans cet article, nous traiterons de l'équation de Navier-Stokes pour un fluide incompressible, le résoudrons numériquement et ferons une belle simulation qui fonctionne par calcul parallèle sur CUDA. L'objectif principal est de montrer comment vous pouvez appliquer les mathématiques sous-jacentes à l'équation dans la pratique lors de la résolution du problème de la modélisation des liquides et des gaz.




Remarque: si vous lisez le Habr depuis un appareil mobile et que vous ne voyez pas les formules, utilisez la version complète du site

Équation de Navier-Stokes pour un fluide incompressible

$$

$${\ partial {\ bf \ vec {u}} \ over {\ partial t}} = - ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}} - {1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$$

Je pense que tout le monde a entendu parler de cette équation au moins une fois, certains, peut-être même de manière analytique, ont résolu ses cas particuliers, mais en termes généraux, ce problème n'est pas résolu jusqu'à présent. Bien sûr, nous ne fixons pas l'objectif de résoudre le problème du millénaire dans cet article, mais nous pouvons toujours lui appliquer la méthode itérative. Mais pour commencer, regardons la notation dans cette formule.

Classiquement, l'équation de Navier-Stokes peut être divisée en cinq parties:

• $$$\ partial {\ bf \ vec {u}} \ over \ partial t$ - désigne le taux de variation de la vitesse du fluide en un point (nous le considérerons pour chaque particule dans notre simulation).
• $$$- ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}}$ - le mouvement du fluide dans l'espace.
• $$$- {1 \ over \ rho} \ nabla {\ bf p}$ La pression exercée sur la particule (ici $$$\ rho$ - coefficient de densité du fluide).
• $$$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ - viscosité du milieu (plus il est grand, plus le liquide résiste à la force appliquée sur sa partie), $$$\ nu$ - coefficient de viscosité).
• $$$\ bf \ vec {F}$ - les forces externes que nous appliquons au fluide (dans notre cas, la force jouera un rôle très spécifique - elle reflétera les actions effectuées par l'utilisateur.

Aussi, puisque nous considérerons le cas d'un fluide incompressible et homogène, nous avons une autre équation: $$${{\ \ nabla \ cdot \ bf \ vec {u}} = 0}$ . L'énergie dans l'environnement est constante, ne va nulle part, ne vient de nulle part.

Il sera erroné de priver tous les lecteurs qui ne sont pas familiers avec l' analyse vectorielle , donc, en même temps et de passer brièvement en revue tous les opérateurs qui sont présents dans l'équation (cependant, je recommande fortement de rappeler ce que sont la dérivée, la différentielle et le vecteur, car ils sous-tendent tout cela ce qui sera discuté ci-dessous).

Nous commençons par l'opérateur nabla, qui est un tel vecteur (dans notre cas, il sera à deux composants, puisque nous modéliserons le fluide dans un espace à deux dimensions):

$$

$$\ nabla = {\ begin {pmatrix} {\ partial \ over \ partial x}, {\ partial \ over \ partial y} \ end {pmatrix}}$$

L'opérateur nabla est un opérateur différentiel vectoriel et peut être appliqué à la fois à une fonction scalaire et à une fonction vectorielle. Dans le cas d'un scalaire, on obtient le gradient de la fonction (le vecteur de ses dérivées partielles), et dans le cas d'un vecteur, la somme des dérivées partielles le long des axes. La caractéristique principale de cet opérateur est qu'à travers lui, vous pouvez exprimer les principales opérations de l'analyse vectorielle - grad ( gradient ), div ( divergence ), rot ( rotor ) et $$$\ nabla ^ 2$ ( Opérateur Laplace ). Il convient de noter immédiatement que l'expression $$$({\ bf \ vec {u} \ cdot \ nabla}) {\ bf \ vec {u}}$ ne revient pas à $$$({\ nabla \ cdot \ bf \ vec {u}}) {\ bf \ vec {u}}$ - l'opérateur nabla n'a pas de commutativité.

Comme nous le verrons plus loin, ces expressions sont sensiblement simplifiées lors du déplacement vers un espace discret dans lequel nous effectuerons tous les calculs, alors ne vous inquiétez pas si pour le moment vous ne savez pas trop quoi faire avec tout cela. Après avoir divisé la tâche en plusieurs parties, nous allons successivement résoudre chacune d'elles et présenter tout cela sous la forme de l'application séquentielle de plusieurs fonctions à notre environnement.

Solution numérique de l'équation de Navier-Stokes

Pour représenter notre fluide dans le programme, nous devons obtenir une représentation mathématique de l'état de chaque particule fluide à un moment arbitraire. La méthode la plus pratique pour cela consiste à créer un champ vectoriel de particules stockant leur état sous la forme d'un plan de coordonnées:



Dans chaque cellule de notre réseau bidimensionnel, nous enregistrerons la vitesse des particules à la fois $$$t: {\ bf \ vec {u}} = u ({\ bf \ vec {x}}, t), \ bf \ vec {x} = \ begin {pmatrix} x, y \ end {pmatrix}$ et la distance entre les particules est indiquée par $$$\ delta x$ et $$$\ delta y$ en conséquence. Dans le code, il nous suffira de changer la valeur de la vitesse à chaque itération, en résolvant un ensemble de plusieurs équations.

Nous exprimons maintenant le gradient, la divergence et l'opérateur de Laplace en tenant compte de notre grille de coordonnées ( $$$i, j$ - indices dans le tableau, $$$\ bf \ vec {u} _ {(x)}, \ vec {u} _ {(y)}$ - en prenant les composantes correspondantes du vecteur):

Nous pouvons simplifier davantage les formules discrètes d'opérateurs vectoriels si nous supposons que $$$\ delta x = \ delta y = 1$ . Cette hypothèse n'affectera pas considérablement la précision de l'algorithme, cependant, elle réduit le nombre d'opérations par itération et rend généralement les expressions plus agréables à l'œil.

Mouvement des particules

Ces énoncés ne fonctionnent que si nous pouvons trouver les particules les plus proches par rapport à celle considérée à l'heure actuelle. Afin d'annuler tous les coûts possibles associés à leur recherche, nous suivrons non pas leur mouvement, mais d' où viennent les particules au début de l'itération en projetant la trajectoire du mouvement vers l'arrière dans le temps (en d'autres termes, soustrayez le vecteur vitesse à partir duquel le temps passe de position actuelle). En utilisant cette technique pour chaque élément du tableau, nous serons sûrs que toute particule aura des «voisins»:



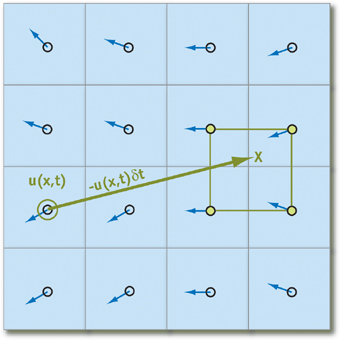
Mettre ça $$$q$ - un élément du tableau qui stocke l'état de la particule, on obtient la formule suivante pour calculer son état dans le temps $$$\ delta t$ (nous pensons que tous les paramètres nécessaires sous forme d'accélération et de pression ont déjà été calculés):

$$

$$q ({{\ \ vec {\ bf x}}, t + \ delta t}) = q ({{\ \ bf \ vec {x}} - {\ bf \ vec {u}} \ delta t}, t)$$

On constate immédiatement que pour suffisamment petit $$$\ delta t$ et nous ne pouvons jamais aller au-delà des limites de la cellule, il est donc très important de choisir la bonne impulsion que l'utilisateur donnera aux particules.

Afin d'éviter toute perte de précision dans le cas d'une projection atteignant la limite de la cellule ou dans le cas de coordonnées non entières, nous effectuerons une interpolation bilinéaire des états des quatre particules les plus proches et la prendrons comme vraie valeur au point. En principe, une telle méthode ne réduira pratiquement pas la précision de la simulation, et en même temps, elle est assez simple à mettre en œuvre, nous allons donc l'utiliser.

La viscosité

Chaque liquide a une certaine viscosité, la capacité d'empêcher l'influence de forces externes sur ses parties (le miel et l'eau en seront un bon exemple, dans certains cas leurs coefficients de viscosité diffèrent d'un ordre de grandeur). La viscosité affecte directement l'accélération acquise par le liquide, et peut être exprimée par la formule ci-dessous, si par souci de concision nous omettons d'autres termes pendant un certain temps:

$$

$${\ partial \ vec {\ bf u} \ over \ partial t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$$

. Dans ce cas, l'équation itérative de la vitesse prend la forme suivante:

$$

$$u ({\ bf \ vec {x}}, t + \ delta t) = u ({\ bf \ vec {x}}, t) + \ nu \ delta t \ nabla ^ 2 \ bf \ vec {u }$$

Nous allons légèrement transformer cette égalité, la concrétiser $$$\ bf A \ vec {x} = \ vec {b}$ (forme standard d'un système d'équations linéaires):

$$

$$({\ bf I} - \ nu \ delta t \ nabla ^ 2) u ({\ bf \ vec {x}}, t + \ delta t) = {u ({\ bf \ vec {x}}, t )}$$

où $$$\ bf I$ Est la matrice d'identité. Nous avons besoin de telles transformations afin d'appliquer ultérieurement la méthode de Jacobi pour résoudre plusieurs systèmes d'équations similaires. Nous en discuterons également plus tard.

Forces externes

L'étape la plus simple de l'algorithme est l'application de forces externes au milieu. Pour l'utilisateur, cela se traduira par des clics sur l'écran avec la souris ou son mouvement. La force externe peut être décrite par la formule suivante, que nous appliquons pour chaque élément de la matrice ( $$$\ vec {\ bf G}$ - vecteur d'élan $$$x_p, y_p$ - position de la souris $$$x, y$ - coordonnées de la cellule courante, $$$r$ - rayon d'action, paramètre d'échelle):

$$

$$\ vec {\ bf F} = \ vec {\ bf G} \ delta t {\ bf exp} \ left (- {{(x - x_p) ^ 2 + (y - y_p) ^ 2} \ over r} \ droite)$$

Un vecteur d'impulsion peut être facilement calculé comme la différence entre la position précédente de la souris et la position actuelle (s'il y en avait une), et ici, vous pouvez toujours être créatif. C'est dans cette partie de l'algorithme que l'on peut introduire l'ajout de couleurs à un liquide, son illumination, etc. Les forces externes peuvent également inclure la gravité et la température, et bien qu'il ne soit pas difficile de mettre en œuvre de tels paramètres, nous ne les examinerons pas dans cet article.

La pression

La pression dans l'équation de Navier-Stokes est la force qui empêche les particules de remplir tout l'espace dont elles disposent après leur avoir appliqué une force externe. Immédiatement, son calcul est très difficile, mais notre problème peut être grandement simplifié en appliquant le théorème de décomposition de Helmholtz .

Appeler $$$\ bf \ vec {W}$ champ vectoriel obtenu après calcul du déplacement, des forces externes et de la viscosité. Il aura une divergence non nulle, ce qui contredit la condition d'incompressibilité du liquide ( $$$\ nabla \ cdot \ bf \ vec {u} = 0$ ), et pour y remédier, il est nécessaire de calculer la pression. Selon le théorème de décomposition de Helmholtz, $$$\ bf \ vec {W}$ peut être représenté comme la somme de deux champs:

$$

$$\ bf \ vec {W} = \ vec {u} + \ nabla p$$

où $$$\ bf u$ - c'est le champ vectoriel que nous recherchons avec une divergence nulle. Aucune preuve de cette égalité ne sera donnée dans cet article, mais à la fin, vous trouverez un lien avec une explication détaillée. Nous pouvons appliquer l'opérateur nabla des deux côtés de l'expression pour obtenir la formule suivante pour calculer le champ de pression scalaire:

$$

$$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot (\ vec {u} + \ nabla p) = \ nabla \ cdot \ vec {u} + \ nabla ^ 2 p = \ nabla ^ 2 p$$

L'expression écrite ci-dessus est l'équation de Poisson pour la pression. Nous pouvons également le résoudre par la méthode de Jacobi susmentionnée, et ainsi trouver la dernière variable inconnue dans l'équation de Navier-Stokes. En principe, les systèmes d'équations linéaires peuvent être résolus de diverses manières différentes et sophistiquées, mais nous nous attarderons toujours sur les plus simples d'entre elles, afin de ne pas alourdir davantage cet article.

Conditions limites et initiales

Toute équation différentielle modélisée sur un domaine fini nécessite des conditions initiales ou limites correctement spécifiées, sinon nous sommes très susceptibles d'obtenir un résultat physiquement incorrect. Les conditions aux limites sont établies pour contrôler le comportement du fluide près des bords de la grille de coordonnées, et les conditions initiales spécifient les paramètres des particules au moment du démarrage du programme.

Les conditions initiales seront très simples - au départ, le fluide est stationnaire (la vitesse des particules est nulle) et la pression est également nulle. Les conditions aux limites seront définies pour la vitesse et la pression par les formules données:

$$

$${\ bf \ vec {u} _ {0, j} + \ bf \ vec {u} _ {1, j} \ over 2 \ delta y} = 0, {\ bf \ vec {u} _ {i , 0} + \ bf \ vec {u} _ {i, 1} \ over 2 \ delta x} = 0$$

$$

$${\ bf p_ {0, j} - \ bf p_ {1, j} \ over \ delta x} = 0, {\ bf p_ {i, 0} - \ bf p_ {i, 1} \ over \ delta y} = 0$$

Ainsi, la vitesse des particules sur les bords sera opposée à la vitesse sur les bords (ainsi elles se repousseront du bord), et la pression est égale à la valeur immédiatement à côté de la frontière. Ces opérations doivent être appliquées à tous les éléments de délimitation du tableau (par exemple, il existe une taille de grille $$$N \ fois M$ , nous appliquons ensuite l'algorithme pour les cellules marquées en bleu sur la figure):

Teinture

Avec ce que nous avons maintenant, vous pouvez déjà trouver beaucoup de choses intéressantes. Par exemple, pour réaliser la propagation du colorant dans un liquide. Pour ce faire, il suffit de maintenir un autre champ scalaire, qui serait responsable de la quantité de peinture à chaque point de la simulation. La formule de mise à jour du colorant est très similaire à la vitesse et s'exprime comme suit:

$$

$${\ partial d \ over \ partial t} = {- (\ vec {\ bf u} \ cdot \ nabla) d} + \ gamma \ nabla ^ 2d + S$$

Dans la formule $$$S$ responsable de reconstituer la zone avec un colorant (éventuellement selon l'endroit où l'utilisateur clique), $$$d$ est directement la quantité de colorant au point, et $$$\ gamma$ - coefficient de diffusion. Le résoudre n'est pas difficile, car tous les travaux de base sur la dérivation des formules ont déjà été effectués, et il suffit de faire quelques substitutions. La peinture peut être implémentée dans le code en tant que couleur au format RVB, et dans ce cas, la tâche est réduite à des opérations avec plusieurs valeurs réelles.

Tourbillon

L'équation de tourbillon n'est pas une partie directe de l'équation de Navier-Stokes, mais c'est un paramètre important pour une simulation plausible du mouvement d'un colorant dans un liquide. En raison du fait que nous produisons un algorithme sur un champ discret, ainsi qu'en raison de pertes de précision des valeurs à virgule flottante, cet effet est perdu, et nous devons donc le restaurer en appliquant une force supplémentaire à chaque point de l'espace. Le vecteur de cette force est désigné par $$$\ bf \ vec {T}$ et est déterminé par les formules suivantes:

$$

$$\ bf \ omega = \ nabla \ times \ vec {u}$$

$$

$$\ vec {\ eta} = \ nabla | \ omega |$$

$$

$$\ bf \ vec {\ psi} = {\ vec {\ eta} \ over {| \ vec {\ eta} |}}$$

$$

$$\ bf \ vec {T} = \ epsilon (\ vec {\ psi} \ times \ omega) \ delta x$$

$$$\ omega$ il y a le résultat de l'application du rotor sur le vecteur vitesse (sa définition est donnée en début d'article), $$$\ vec \ eta$ - gradient du champ scalaire de valeurs absolues $$$\ omega$ . $$$\ vec \ psi$ représente un vecteur normalisé $$$\ vec \ eta$ et $$$\ epsilon$ Est une constante qui contrôle la taille des vortex dans notre fluide.

Méthode de Jacobi pour résoudre des systèmes d'équations linéaires

En analysant les équations de Navier-Stokes, nous avons trouvé deux systèmes d'équations - l'un pour la viscosité et l'autre pour la pression. Ils peuvent être résolus par un algorithme itératif, qui peut être décrit par la formule itérative suivante:

$$

$$x ^ {(k + 1)} _ {i, j} = {{x ^ {(k)} _ {i-1, j} + x ^ {(k)} _ {i + 1, j} + x ^ {(k)} _ {i, j-1} + x ^ {(k)} _ {i, j + 1} + \ alpha b_ {i, j}} \ over \ beta}$$

Pour nous $$$x$ - éléments de tableau représentant un champ scalaire ou vectoriel. $$$k$ - le nombre d'itérations, nous pouvons l'ajuster afin d'augmenter la précision du calcul ou vice versa pour le réduire et augmenter la productivité.

Pour calculer la viscosité, nous substituons: $$$x = b = \ bf \ vec {u}$ , $$$\ alpha = {1 \ over \ nu \ delta t}$ , $$$\ beta = 4+ \ alpha$ , voici le paramètre $$$\ beta$ - la somme des poids. Ainsi, nous devons stocker au moins deux champs de vitesse vectorielle afin de lire indépendamment les valeurs d'un champ et de les écrire dans un autre. En moyenne, pour calculer le champ de vitesse par la méthode Jacobi, il est nécessaire d'effectuer 20 à 50 itérations, ce qui est beaucoup si nous effectuons des calculs sur le CPU.

Pour l'équation de pression, nous faisons la substitution suivante: $$$x = p$ , $$$b = \ nabla \ bf \ cdot \ vec {W}$ , $$$\ alpha = -1$ , $$$\ beta = 4$ . En conséquence, nous obtenons la valeur $$$p_ {i, j} \ delta t$ au point. Mais comme il n'est utilisé que pour calculer le gradient soustrait du champ de vitesse, des transformations supplémentaires peuvent être omises. Pour un champ de pression, il est préférable d'effectuer 40 à 80 itérations, car à des nombres inférieurs, l'écart devient perceptible.

Implémentation d'algorithme

Nous implémenterons l'algorithme en C ++, nous avons également besoin du Cuda Toolkit (vous pouvez lire comment l'installer sur le site Web de Nvidia), ainsi que de SFML . Nous avons besoin de CUDA pour paralléliser l'algorithme, et SFML ne sera utilisé que pour créer une fenêtre et afficher une image à l'écran (En principe, cela peut être écrit en OpenGL, mais la différence de performances ne sera pas significative, mais le code augmentera de 200 lignes supplémentaires).

Boîte à outils Cuda

Tout d'abord, nous allons parler un peu de la façon d'utiliser le Cuda Toolkit pour paralléliser les tâches. Un guide plus détaillé est fourni par Nvidia lui-même, donc ici nous nous limitons aux plus nécessaires. Il est également supposé que vous avez pu installer le compilateur et que vous avez pu créer un projet de test sans erreur.

Pour créer une fonction qui s'exécute sur le GPU, vous devez d'abord déclarer combien de noyaux nous voulons utiliser et combien de blocs de noyaux nous devons allouer. Pour cela, le Cuda Toolkit nous fournit une structure spéciale - dim3 , en définissant par défaut toutes ses valeurs x, y, z sur 1. En le spécifiant comme argument lors de l'appel de la fonction, nous pouvons contrôler le nombre de noyaux alloués. Puisque nous travaillons avec un tableau à deux dimensions, nous devons définir seulement deux champs dans le constructeur: x et y :

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads); 

où size_x et size_y sont la taille du tableau en cours de traitement. La signature et l'appel de fonction sont les suivants (les crochets à triple angle sont traités par le compilateur Cuda):

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host 

Dans la fonction elle-même, vous pouvez restaurer les indices d'un tableau à deux dimensions via le numéro de bloc et le numéro de noyau dans ce bloc à l'aide de la formule suivante:

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; 

Il convient de noter que la fonction exécutée sur la carte vidéo doit être marquée avec la balise __global__ , et également retourner nulle , donc le plus souvent, les résultats des calculs sont écrits dans le tableau passé en argument et préalloués dans la mémoire de la carte vidéo.

Les fonctions CudaMalloc et CudaFree sont responsables de la libération et de l'allocation de mémoire sur la carte vidéo. Nous pouvons opérer sur des pointeurs vers la zone mémoire qu'ils retournent, mais nous ne pouvons pas accéder aux données du code principal. La façon la plus simple de renvoyer les résultats des calculs est d'utiliser cudaMemcpy , similaire à la mémoire standard, mais capable de copier des données d'une carte vidéo vers la mémoire principale et vice versa.

SFML et rendu de fenêtre

Armé de toutes ces connaissances, nous pouvons enfin passer directement à l'écriture de code. Pour commencer, créons le fichier main.cpp et y plaçons tout le code auxiliaire pour le rendu de la fenêtre:


ligne au début de la fonction principale

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); 

crée une image RGBA sous la forme d'un tableau unidimensionnel de longueur constante. Nous le transmettrons avec d'autres paramètres (position de la souris, différence entre les images) à la fonction computeField . Ces dernières, ainsi que plusieurs autres fonctions, sont déclarées dans kernel.cu et appellent le code exécuté sur le GPU. Vous pouvez trouver de la documentation sur l'une des fonctions sur le site Web SFML, rien de super intéressant ne se passe dans le code du fichier, donc nous ne nous arrêterons pas là longtemps.

GPU Computing

Pour commencer à écrire du code sous gpu, créez d'abord un fichier kernel.cu et définissez-y plusieurs classes auxiliaires: Color3f, Vec2, Config, SystemConfig :


L'attribut __host__ devant le nom de la méthode signifie que le code peut être exécuté sur le CPU, __device__ , au contraire, oblige le compilateur à collecter du code sous le GPU. Le code déclare des primitives pour travailler avec des vecteurs à deux composants, la couleur, des configurations avec des paramètres qui peuvent être modifiés au moment de l'exécution, ainsi que plusieurs pointeurs statiques vers des tableaux, que nous utiliserons comme tampons pour les calculs.

cudaInit et cudaExit sont également définis de manière assez triviale:


Dans la fonction d'initialisation, nous allouons de la mémoire aux tableaux bidimensionnels, spécifions un tableau de couleurs que nous utiliserons pour peindre le liquide et définirons également les valeurs par défaut dans la configuration. Dans cudaExit, nous libérons simplement tous les tampons. Aussi paradoxal que cela puisse paraître, pour stocker des tableaux bidimensionnels, il est très avantageux d'utiliser des tableaux unidimensionnels, dont l'accès sera effectué avec l'expression suivante:

 array[y * size_x + x]; // equals to array[y][x] 

Nous commençons l'implémentation de l'algorithme direct avec la fonction de déplacement de particules. Les champs oldField et newField (le champ d'où proviennent les données et où elles sont écrites), la taille du tableau, ainsi que le delta temporel et le coefficient de densité (utilisés pour accélérer la dissolution du colorant dans le liquide et rendre le milieu peu sensible à l' advect, sont transférés à advect actions utilisateur). La fonction d' interpolation bilinéaire est implémentée de manière classique en calculant des valeurs intermédiaires:


Il a été décidé de diviser la fonction de diffusion de la viscosité en plusieurs parties: computeDiffusion est appelé à partir du code principal, qui appelle diffuse et computeColor un nombre prédéterminé de fois, puis échange le tableau d'où nous prenons les données et celui où nous les écrivons. C'est le moyen le plus simple de mettre en œuvre un traitement parallèle des données, mais nous dépensons deux fois plus de mémoire.

Les deux fonctions provoquent des variations de la méthode Jacobi. Le corps de jacobiColor et jacobiVelocity vérifie immédiatement que les éléments actuels ne sont pas à la frontière - dans ce cas, nous devons les définir conformément aux formules décrites dans la section Limites et conditions initiales .


L'utilisation de la force externe est implémentée à travers une seule fonction - applyForce , qui prend comme argument la position de la souris, la couleur du colorant, ainsi que le rayon d'action. Avec son aide, nous pouvons donner de la vitesse aux particules, ainsi que les peindre. L'exposant fraternel vous permet de rendre la zone pas trop nette et en même temps assez claire dans le rayon spécifié.


Le calcul du tourbillon est déjà un processus plus complexe, nous l'implémentons donc dans computeVorticity et applyVorticity , nous notons également que pour eux, il est nécessaire de définir deux opérateurs vectoriels tels que curl (rotor) et absGradient (gradient des valeurs de champ absolues). Pour spécifier des effets de vortex supplémentaires, nous multiplions $$$y$ composante du vecteur de gradient sur $$$-1$ , puis normalisez-le en divisant par la longueur (sans oublier de vérifier que le vecteur n'est pas nul):


La prochaine étape de l'algorithme sera le calcul du champ de pression scalaire et sa projection sur le champ de vitesse. Pour ce faire, nous devons implémenter 4 fonctions: la divergence , qui prendra en compte la divergence de vitesse, jacobiPressure , qui implémente la méthode Jacobi pour la pression, et computePressure avec computePressureImpl , qui itère les calculs de champ:


La projection tient dans deux petites fonctions - projet et le gradient qu'elle appelle la pression. Cela peut être dit la dernière étape de notre algorithme de simulation:


Après la projection, nous pouvons procéder en toute sécurité au rendu de l'image dans le tampon et divers post-effets. La fonction de peinture copie les couleurs du champ de particules dans le réseau RGBA. La fonction applyBloom a également été implémentée, qui met en évidence le liquide lorsque le curseur est placé dessus et que le bouton de la souris est enfoncé. Par expérience, cette technique rend l'image plus agréable et intéressante pour les yeux de l'utilisateur, mais ce n'est pas du tout nécessaire.

En post-traitement, vous pouvez également mettre en évidence les endroits où le fluide a la vitesse la plus élevée, changer de couleur en fonction du vecteur de mouvement, ajouter divers effets, etc., mais dans notre cas, nous nous limiterons à une sorte de minimum, car même avec lui, les images sont très fascinantes (surtout en dynamique) :


Et à la fin, nous avons encore une fonction principale que nous appelons depuis main.cpp - computeField . Il relie tous les éléments de l'algorithme, appelle le code sur la carte vidéo et copie également les données de gpu vers cpu. Il contient également le calcul du vecteur momentum et le choix de la couleur du colorant, que nous passons pour appliquer Force :

Conclusion

Dans cet article, nous avons analysé un algorithme numérique pour résoudre l'équation de Navier-Stokes et écrit un petit programme de simulation pour un fluide incompressible. Peut-être que nous n'avons pas compris toutes les subtilités, mais j'espère que le matériel s'est avéré intéressant et utile pour vous, et a au moins servi de bonne introduction au domaine de la modélisation des fluides.

En tant qu'auteur de cet article, j'apprécierai sincèrement tous les commentaires et ajouts, et j'essaierai de répondre à toutes vos questions sous ce post.

Matériel supplémentaire

Vous pouvez trouver tout le code source dans cet article dans mon référentiel Github . Toute suggestion d'amélioration est la bienvenue.

Le matériel original qui a servi de base à cet article, vous pouvez le lire sur le site officiel de Nvidia. Il présente également des exemples de mise en œuvre de parties de l'algorithme dans le langage des shaders:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

La preuve du théorème de décomposition de Helmholtz et une énorme quantité de matériel supplémentaire sur la mécanique des fluides se trouvent dans ce livre (en anglais, voir la section 1.2):
Chorin, AJ et JE Marsden. 1993. Une introduction mathématique à la mécanique des fluides. 3e éd. Springer

La chaîne d'un YouTube anglophone, faisant du contenu de haute qualité lié aux mathématiques, et la solution d'équations différentielles en particulier (anglais). Vidéos très visuelles qui aident à comprendre l'essence de beaucoup de choses en mathématiques et en physique:
3Blue1Brown -
Equations différentielles YouTube (3Blue1Brown)

Je remercie également WhiteBlackGoose pour son aide dans la préparation du matériel pour l'article.

---

Et à la fin, un petit bonus - quelques belles captures d'écran prises dans le programme: Flux


direct (paramètres par défaut)


Whirlpool (grand rayon dans applyForce)


Wave (haut tourbillon + diffusion)

Aussi, à la demande générale, j'ai ajouté une vidéo avec la simulation: