Salut
Assurément, tout le monde est arrivé à assister à une évaluation du judas du degré de similitude de l'enfant avec les parents: quelque chose comme "papa versé, mais il ressemble aussi à maman !!!"
(
extrait d'ici )
Comme dans l'exemple de l'image, vous pouvez évaluer le degré de similitude en pourcentage. Vous pouvez également utiliser des proches pour décrire plus précisément le visage du bébé sous la forme d'une somme pondérée des proches des parents ...
Et il ressemblera et sera perçu tout naturellement pour une personne «ordinaire» qui n'est pas associée à l'anthropologie ou, par exemple, à la médecine légale. Pour un professionnel dans le domaine de l'analyse et de la reconnaissance faciale, un visage humain est plus probablement un ensemble de paramètres. C'est-à-dire un point (un ensemble de coordonnées) dans un espace avec une base (axes correspondant aux paramètres). Et si nous décrivons le visage de l'enfant en comparaison avec ses proches, alors le point correspondant au visage de l'enfant apparaîtra probablement dans cet espace de paramètres à l'intérieur de la coque convexe du nuage de points correspondant aux visages du plus proche parent (mais ce n'est pas exact).
En fait, de quoi je parle ... Ces deux approches de la description des visages correspondent à deux systèmes de coordonnées:
- barycentrique, description d'un point dans l'espace (dans notre exemple: visage) à travers un mélange pondéré d'autres points;
- affine, une description d'un point dans l'espace à travers des coordonnées dans une certaine base.
Alors, quelles sont les coordonnées barycentriques?
Laissez entrer
-espace dimensionnel donné
pointer
avec des vecteurs de rayon
,
. De plus, aucun des points ne se trouve dans la coque linéaire des vecteurs de rayon des points restants ... En termes simples, c'est assez simple: que ces points forment une figure qui ne peut pas être entièrement représentée dans un espace avec une dimension inférieure à
.
Dans le cas de l'espace unidimensionnel (ligne), nous avons besoin de 2 points non coïncidents, dans le cas de l'espace bidimensionnel - un triangle non dégénéré, dans le cas de l'espace tridimensionnel - un tétraèdre.
Puis n'importe quel point dans l'espace
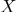
peut être représenté par un vecteur rayon
:
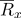
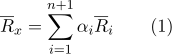
Ensemble
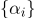
et il y a des coordonnées barycentriques.
Comment les coordonnées barycentriques sont-elles meilleures / pires que les affines?
Commençons par les inconvénients relatifs:
- dans la représentation barycentrique, nous avons besoin d'une coordonnée de plus que dans la représentation affine;
- la distance entre les points spécifiés barycentriquement ne peut pas être calculée directement dans ces coordonnées.
En partie, le premier inconvénient est compensé par le fait que, malgré la nécessité d'utiliser
coordonnées barycentriques lors de la description d'un point
-Espace dimensionnel, le nombre de degrés n'augmente pas. Les coordonnées barycentriques définies dans la formule (1) sont liées par la relation:
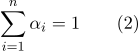
Quant au deuxième inconvénient, s'il est nécessaire de calculer la distance entre les points représentés barycentriquement, alors il est logique de calculer les produits scalaires
et utiliser l'analogue de la distance de Mahalanobis.
Quels sont les bonus liés à l'utilisation des coordonnées barycentriques?
- Les coordonnées barycentriques sont invariantes aux transformations affines de l'espace. Cette propriété est utilisée, par exemple, pour l'interpolation linéaire en infographie. Laissez les coordonnées de texture être définies aux sommets d'un élément de surface triangulaire
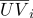et normales 
( 
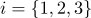), alors chaque point de cette section de surface aura des coordonnées barycentriques 
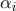ses coordonnées de texture 
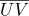et normal 
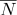peut être calculé comme:
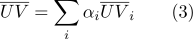
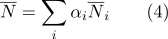
- Par coordonnées barycentriques, il est facile de déterminer si un point appartient 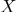parties d'espace délimitées par un polyèdre à sommets : ceci n'est fait que si
. L'égalité de la i-ème coordonnée barycentrique 1 signifie que le point 
coïncide avec . Si plusieurs coordonnées barycentriques sont égales à 0, cela signifie que le point appartient à un sous-espace couvert par les vecteurs de rayon des points restants dont les coordonnées correspondantes sont supérieures à 0.
Peut-être sont-ils très difficiles à calculer?
Pas plus compliqué que n'importe quelle transformation linéaire du système de coordonnées. Parce que, par essence, le calcul des coordonnées barycentriques est une telle transformation.
Nous réécrivons le vecteur rayon des points sous la forme suivante:
où
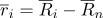
- un vecteur radial dans le système de coordonnées centré en un point
.
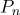
La formule (1) peut alors être réécrite sous la forme suivante:
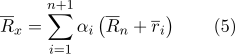
Nous révélerons les parenthèses dans la somme:
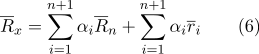
Selon la propriété (2):
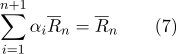
En conséquence:
,
où
Étant donné (2), nous nous limitons au calcul des n premières coordonnées barycentriques. Imaginez la transition vers les coordonnées barycentriques comme une transformation linéaire:
,
où
- vecteur n de coordonnées barycentriques (sauf le dernier),
- matrice de transformation.
Étant donné les propriétés de la représentation barycentrique, si
remplacer l'un des vecteurs
(
), on obtient alors un vecteur à zéro composante, sauf un i-ième, qui sera égal à 1.
Si la matrice
multiplier par matrice
composé de colonnes de
, alors nous devrions obtenir la matrice d'identité (une matrice avec des uns sur la diagonale principale et des zéros dans les éléments restants):
,
où
,
La matrice d'identité (
- Symbole Kronecker: 1 si
sinon 0).
De (10) on trouve
:
Ainsi, avoir un ensemble de points avec des vecteurs de rayon
,
on peut calculer la matrice à convertir en coordonnées barycentriques:
En utilisant cette matrice, nous pouvons obtenir le premier
coordonnées du point barycentrique
avec vecteur de rayon
:
En utilisant à nouveau la relation (2), nous obtenons la dernière coordonnée barycentrique:
Conclusion
Peut-être qu'à première vue, le barycentrique semble également maladroit et complexe. Mais en fait, c'est un outil très pratique et indispensable dans de nombreuses tâches, auquel vous vous habituez assez rapidement. Parce qu'il n'y a pas de magie ici, c'est de l'algèbre linéaire dans sa forme la plus pure!