Régression linéaire et descente de gradient

Que les indicateurs X et Y, qui ont une expression quantitative, soient étudiés dans un certain domaine.

De plus, il y a tout lieu de penser que l'indicateur Y dépend de l'indicateur X. Cette position peut être à la fois une hypothèse scientifique et reposer sur le bon sens élémentaire. Par exemple, prenez les épiceries.

Désigner par:

X - surface de vente (m²)

Y - chiffre d'affaires annuel (millions p.)

De toute évidence, plus la zone d'échange est élevée, plus le chiffre d'affaires annuel est élevé (nous supposons une relation linéaire).

Imaginez que nous ayons des données sur quelques n magasins (espace de vente au détail et chiffre d'affaires annuel) - notre ensemble de données et k espace de vente au détail (X), pour lesquels nous voulons prédire le chiffre d'affaires annuel (Y) - notre tâche.

Nous supposons que notre valeur de Y dépend de X sous la forme: Y = a + b * X

Pour résoudre notre problème, nous devons choisir les coefficients a et b.

Tout d'abord, définissons des valeurs aléatoires a et b. Après cela, nous devons déterminer la fonction de perte et l'algorithme d'optimisation.

Pour ce faire, nous pouvons utiliser la fonction de perte quadratique moyenne ( MSELoss ). Il est calculé par la formule:



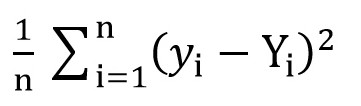
Où y [i] = a + b * x [i] après a = rand () et b = rand (), et Y [i] est la valeur correcte pour x [i].
A ce stade, nous avons l'écart type (une certaine fonction de a et b). Et il est évident que, plus la valeur de cette fonction est petite, plus les paramètres a et b sont sélectionnés avec précision par rapport à ces paramètres qui décrivent la relation exacte entre la surface de l'espace de vente et le chiffre d'affaires dans cette pièce.

Maintenant, nous pouvons commencer à utiliser la descente de gradient (juste pour minimiser la fonction de perte).

Descente en pente

Son essence est très simple. Par exemple, nous avons une fonction:

y = x*x + 4 * x + 3 

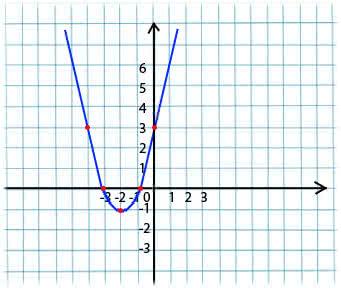
Nous prenons une valeur arbitraire de x dans le domaine de définition de la fonction. Imaginez que c'est le point x1 = -4.

Ensuite, nous prenons la dérivée par rapport à x de cette fonction au point x1 (si la fonction dépend de plusieurs variables (par exemple, a et b), alors nous devons prendre les dérivées partielles pour chacune des variables). y '(x1) = -4 <0

Nous obtenons maintenant une nouvelle valeur pour x: x2 = x1 - lr * y '(x1). Le paramètre lr (taux d'apprentissage) vous permet de définir la taille du pas. On obtient ainsi:

Si la dérivée partielle à un point donné x1 <0 (la fonction diminue), alors nous passons au point de minimum local. (x2 sera plus grand que x1)

Si la dérivée partielle à un point donné x1> 0 (la fonction augmente), alors nous nous déplaçons toujours au point de minimum local. (x2 sera inférieur à x1)

En effectuant cet algorithme de manière itérative, nous approcherons du minimum (mais ne l'atteindrons pas).

En pratique, tout cela semble beaucoup plus simple (cependant, je ne présume pas de dire quels coefficients a et b conviendront le mieux avec le cas ci-dessus avec les magasins, nous prenons donc une dépendance de la forme y = 1 + 2 * x pour générer l'ensemble de données, puis former notre modèle sur cet ensemble de données):
(Le code est écrit ici )

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

Après avoir compilé le code, vous pouvez voir que les valeurs initiales de a et b étaient loin des 1 et 2 requis, respectivement, et les valeurs finales sont très proches.

Je vais clarifier un peu pourquoi a_grad et b_grad sont considérés de cette façon.
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) . La dérivée partielle de F par rapport à a sera -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error . La dérivée partielle de F par rapport à b sera -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error . Nous prenons la valeur moyenne (mean()) car error et x_train et y_train sont des tableaux de valeurs, a et b sont des scalaires.

Matériaux utilisés dans l'article:

versdatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html