⚪️ ⏯️ 🍇 Le nombre sous-jacent à la musique moderne 🕝 🐰 👩🏾‍🚒

Pourquoi douze?

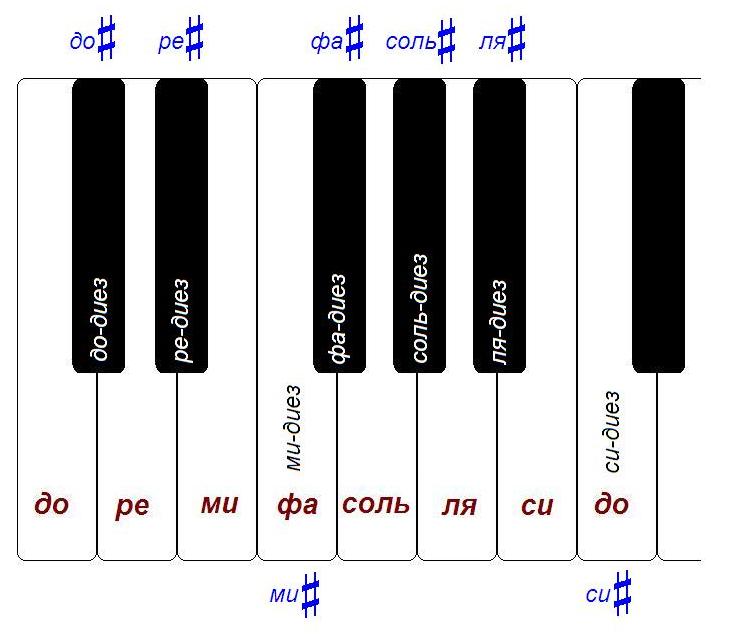
Si vous regardez le clavier, vous verrez que chaque octave contient 12 demi-tons.
Dans le cas du piano, cela signifie seulement qu'entre, par exemple, «vers» la première octave et «vers» la deuxième octave, il y a 11 touches. Avec l'un des "do" (par exemple, à la deuxième octave), nous obtenons 12 touches: do #, re, re #, mi, fa, fa #, salt, salt #, la, la #, si, do.

Mais pourquoi 12?

Peut-être que c'est juste un accident? Nos ancêtres ont aimé le nombre 12, ils en ont 12 partout: 12 mois, 12 signes du zodiaque, 12 tribus d'Israël, 12 apôtres, ... et ici ils ont décidé, que ce soit 12, et ainsi il a été commandé. Ou existe-t-il encore une loi objective, et ce nombre n'est pas accidentel?

Dans cet article, je vais essayer de démontrer que ce n'est pas un accident. Des exigences suffisamment générales, tout à fait naturelles pour la musique moderne (occidentale), avec une nécessité mathématique, nous conduisent au nombre 12. Il est intéressant de noter que la raison pour laquelle nous avons cette valeur est la propriété d'un autre nombre (voir la fin de l'article). On peut même dire qu'il est au cœur du son moderne.

Énoncé du problème

Tout d'abord, essayons de formaliser la tâche.

Nous avons une fréquence de référence $\ omega_0$ . Nous l'appellerons tonique. Nous avons également une octave avec une fréquence $2 \ omega_0$ . Maintenant, nous devons comprendre quelles options pour les fréquences intermédiaires $\ omega_0$ avant $2 \ omega_0$ , telle qu'une mélodie construite sur ces notes sonnerait harmonieusement à nos oreilles?

Je crains que cette formulation, même si elle reflète l'essence de la question, soit encore, d'un point de vue mathématique, assez vague, et une telle question ne peut être répondue sans ambiguïté, ne serait-ce que parce que l'ouïe humaine a une résolution en fréquence assez limitée. Et cela est confirmé par le fait qu'à différentes époques différentes mélodies ont été utilisées, par exemple, Pythagore , des mélodies propres , bien tempérées , uniformément tempérées . Et ils sonnaient et sonnaient tous, du moins pour certaines œuvres, tout à fait acceptables.

Qu'est-ce que l'harmonie?

Nous devons imposer des conditions supplémentaires. Mais d'abord, nous devons répondre à une question importante: que percevons-nous comme un son harmonieux?

Regardons deux sons - avec des fréquences $\ omega_1$ et $\ omega_2$ .

Prenez le rapport de ces fréquences. Cette relation peut être représentée comme un produit de nombres $a_1 ^ {k_1} \ cdot a_2 ^ {k_2} \ cdot ... \ cdot a_l ^ {k_l}$ où $inline$ Sont des nombres premiers, et $inline$ - des entiers, par exemple, ce rapport peut être égal à $2 ^ {- 3} \ cdot3 \ cdot5$ . Et que ces nombres premiers ( $inline$ ) moins, plus harmonieux pour notre oreille cet intervalle sonnera (j'ai trouvé cette déclaration ici (voir le deuxième paragraphe) )

Ainsi, par exemple, le son le plus harmonieux conformément à cette déclaration sera une octave (changement de fréquence de 2 fois). Et les prochains intervalles harmoniques seront le cinquième (changement de fréquence $inline$ fois) et un quart (changement de fréquence $inline$ fois).

Mais pas si simple avec cette déclaration. Ainsi, par exemple, il n'est pas très clair comment le degré affecte. Par exemple, quelle est la multiplication plus harmonieuse par $inline$ ou 7? Je ne sais pas si cette question a été étudiée ou non, et est-il possible, en principe, d'y répondre. De plus, la perception de l'harmonie est une chose plutôt subjective. Ainsi, la musique moderne regorge de sons qui auraient été perçus comme une terrible cacophonie pendant 100-200 ans.

La première condition. Tonique, Quart, Quint, Octave

Cette incertitude n'est pas un problème pour nos petites recherches. Le fait est que la seule conclusion que je veux tirer de cette déclaration est que dans notre cas, en tout cas, il devrait y avoir au moins les intervalles "les plus harmonieux", à savoir une octave, un quart et un cinquième. Autrement dit, avec tonique avec une fréquence $\ omega_0$ et octave avec une fréquence $2 \ omega_0$ il faut aussi avoir un cinquième et un quatrième, avec des fréquences respectivement ${3 \ over 2} \ omega_0$ , ${4 \ over 3} \ omega_0$ ou quelque chose de très proche que nous ne pouvions pas distinguer d'un pur cinquième et quatrième.

Remarque: en fait, seuls les toniques, les quintes et les octaves suffisent. La présence d'un cinquième nous donne immédiatement un quart, en plus d'une octave, et en vertu de la deuxième condition (invariance), qui est décrite ci-dessous, nous devons également avoir un quart et tonique. Autrement dit, la nécessité d'un quart est une conséquence de la présence d'un cinquième et de l'exigence d'invariance.

Et c'est notre première exigence.

La deuxième condition. Invariance

Notre deuxième exigence est l'invariance. Et c'est une exigence importante de la musique moderne. Cette exigence consiste dans le fait que toutes les harmonies d'une touche doivent avoir la même sonorité. Si nous parlons du système moderne, qui est utilisé pour accorder le piano, cela signifie que le cinquième, composé de sept demi-tons, devrait avoir le même son, quel que soit le son à partir duquel il est construit. Autrement dit, le rapport de fréquence entre do et sel doit être le même que pour do # - salt #, re - la, re # - la #, ... et égal $inline$ . Et cette invariance devrait s'appliquer, bien sûr, non seulement au cinquième, mais aussi à tous les intervalles. Un avantage important de ce système est la possibilité de transposer le jeu à n'importe quel intervalle. C'est l'essence du tempérament uniforme.

Je dois dire que cette exigence d'invariance n'est pas si évidente, et cette approche n'a été appliquée relativement récemment qu'au 18e siècle. Les systèmes utilisés auparavant (par exemple, Pythagore et pure) ne possédaient pas une telle propriété. Par exemple, écoutez la Sonate pour piano microtonal (Ben Johnston) , écrite dans un système propre (limite principale = 5). On dirait que le piano n'est pas accordé. Toute la richesse des harmonies modernes repose précisément sur cette invariance. Par exemple, le "Clavier bien tempéré" de Bach est apparu précisément grâce à une nouvelle approche de l'accordage des claviers. C'est cette invariance qui a permis à Bach de créer des séquences harmoniques qui étaient tout simplement impossibles auparavant.

Nous avons donc maintenant toutes les données nécessaires au calcul.

Calcul

Construisons une gamme des toniques aux octaves qui satisfait les deux exigences.
Supposons que dans ce cas, nous obtenons $inline$ sons (dont une octave). C'est $inline$ et est le nombre souhaité. Nous voulons montrer que $inline$ dans nos conditions devrait être 12.

Une conséquence de la deuxième exigence est que l'intervalle entre les fréquences des sons voisins doit être le même et égal $2 ^ {1 \ sur N}$ .

Maintenant, la première exigence dit que dans notre rangée, il devrait y avoir deux sons correspondant (avec une bonne approximation) aux fréquences ${3 \ over 2} \ omega_0$ et ${4 \ over3} \ omega_0$ . Ceci est le cinquième et le quatrième. Supposons qu'un litre soit $inline$ son dans notre rangée, et le cinquième - $inline$ oh. Nous dénotons $inline$ .

Il est facile de voir que le changement de fréquence entre le quatrième et le cinquième (rapport de fréquence) est $inline$ .

Mais, selon notre deuxième condition, cela devrait également être égal $2 ^ {n \ over N}$ .

Nous avons donc obtenu la formule:

$2 ^ {n \ sur N} \ environ 9/8$

Après de simples transformations, on obtient la formule de base:

$n \ approx N (2 \ log_2 {3} - 3) = N \ cdot 0.170$

Il est facile de voir que la solution (bien sûr approximative) est $inline$ où $inline$ - tout nombre naturellement (assez petit, car néanmoins 0,170 diffère de 1/6).

Regardons un cas $inline$ . Dans ce cas $inline$ , $inline$ . C'est-à-dire qu'il s'agit d'une variante du système moderne, uniquement sans demi-tons, uniquement avec des tons (do, re, mi, fa #, salt #, la #, do). Mais, comme vous pouvez le voir, dans ce cas, le quart (f) et le quint (sel) ne tombaient pas dans cette échelle.

Autrement dit, la seule option pour nous peut être

$inline$ où $inline$ - tout nombre naturel ( $inline$ assez petit). Cas $inline$ correspond juste à notre système moderne, qui est appelé le système uniformément capricieux.

Mais pourquoi pas 24 ou plus? La raison est simple - je peux supposer qu'une telle graduation est déjà excessive pour notre perception. Il ne reste donc qu'un seul chiffre: 12.

Si vous n'êtes pas satisfait de la ligne de pensée donnée, alors vous pouvez trouver ici

preuve mathématique rigoureuse

Défi:

Trouver l'entier positif minimum N auquel il y a un entier positif $inline$ tel que $2 ^ {n \ over N}$ différent de $3 $ \ plus de 2 $$ pas plus que $\ delta$ cents .

Solution:

Désigner par $Z_n = N \ cdot (log_2 {3} -1)$ . Ensuite, avec $\ delta <{1200 \ over N}$ (ce qui est vrai pour la gamme de ces $\ delta$ et $inline$ que nous allons considérer) notre tâche est de trouver le minimum $inline$ à quel

${1200 \ over N} \ cdot | Z_n - round (Z_n) | <\ delta$ ,

où $inline$ - fonction arrondie à l'entier le plus proche.

Nous allons résoudre ce problème numériquement.

Il est maintenant temps de décider $\ delta$ .

Quel montant (en cents) de l'écart entre le cinquième pur et «notre cinquième» considérons-nous comme acceptable? Beaucoup de gens entendent, par exemple, que le grand / petit tiers du système uniformément tempéré "triche". Mais ce n'est que d'environ 15 cents par rapport aux intervalles purs. Par conséquent, notre exigence devrait être meilleure que 15 cents. Certaines sources disent qu'à certaines fréquences, les musiciens distinguent jusqu'à 5 - 6 cents. Il est donc sage de prendre $\ delta = 5$ .

Ensuite, le tableau montre clairement que le plus petit $inline$ . Les éléments suivants sont satisfaisants $inline$ .

Remarque:
Prochaine itération, pour chaque $inline$ vous devez également vérifier le son et les autres intervalles. En cas de $inline$ par exemple, les tiers deviennent complètement «faux»: plus de 30 cents (pour un grand tiers).

Notre réponse est donc: $inline$ . Ce qui devait prouver.

Et en passant, il est clair que notre réponse ne changera pas si nous $\ delta = 5$ prenez, par exemple, 10 ou même 15.

Conclusion Numéro sous-jacent

Étonnamment, il s'avère que le nombre sous-jacent au système musical moderne et à la musique contemporaine (européenne) est $\ log_2 {3}$ , à savoir qu'avec une bonne précision (0,1%) l'égalité suivante est vérifiée:

$\ log_2 {3} \ environ 19/12$

Réponses aux commentaires et critiques dans les commentaires

Tout d'abord, merci pour les commentaires intéressants!
Voici mes réponses aux commentaires et critiques les plus importants (à mon avis).

Critique 1. Oeuf ou poulet

Druu: Ecoutez, 12 sons dans une octave correspondaient à un tempérament uniforme en général, donc vous ne pouvez pas justifier 12 sons à l'aide du tempérament, ce sera tout simplement faux.

repaire: C’est exactement la logique en anneau dont je parle: si vous choisissez une musique construite sur un système particulier, il est évident que dans son contexte un système différent est impossible.

À ces remarques et à des remarques similaires, je citerais 2 contre-arguments:

1) si avec une précision suffisante l'égalité $log_2 {3} = 19/12$ , il serait alors impossible de "tirer" un système de tempérament uniforme dans un système pur composé de 12 sons. Le plus fort $log_2 {3}$ différent de $inline$ , plus notre cinquième sonnerait faux. Si ce nombre était (fortement) différent, il n'y aurait pas d'approche uniformément capricieuse des intervalles purs, et, par conséquent, il n'y aurait pas de musique moderne ou, disons, ce serait différent. Par conséquent, la conclusion que les propriétés du nombre est tout à fait logique $log_2 {3}$ sont le fondement de la musique moderne.

2) le deuxième contre-argument est impossible à justifier logiquement, et n'est qu'une supposition, mais il me semble que tout ce raisonnement mérite attention. Essayons de répondre à la question: pourquoi le besoin d'un système uniformément tempéré est-il apparu? Les commentaires ont déjà partiellement répondu. La musique à cette époque (l'époque de la création d'un système uniformément tempérament) utilisait déjà des modulations et de la polyphonie, qui en fait, dans l'ensemble, nécessitaient déjà un tempérament uniforme. Le problème du "faux" son a été résolu par le fait que les musiciens "ajustaient" légèrement le son pendant la représentation. C'était facile à faire pour les cordes (au moins fretless), les vents et les voix (correct, si je me trompe - j'ai fait cette conclusion à partir de vos commentaires). Par exemple, pour le violon - ce n'est qu'un léger changement dans la position des doigts. Mais dès que vous avez été privé d'une telle opportunité (clavecin), tout de suite tout a commencé à sonner. Donc, il semble que ces 12 notes soient apparues non seulement comme ça, mais comme un développement naturel de la musique vers cette possibilité de modulations libres et de polyphonie riche, et cela à son tour est une conséquence de l'invariance. C'était un développement naturel de la musique. Autrement dit, je veux dire que si l'invariance mathématique était possible non pas pour 12 sons, mais, par exemple, pour 10, alors nous (même avant le tempérament uniforme) dans notre gamme aurait 10 sons (dans ce cas, je parle de la manière développement de la musique européenne). Et puis 10 sons de tempérament uniforme seraient tirés sur notre système pur.

Critique 2. L'unicité des douze

Il y a eu beaucoup de critiques au sujet de l'affirmation selon laquelle 12 est le seul nombre raisonnable.

Tout d'abord, en comprenant l'agressivité de cette déclaration et le principe de l'impossibilité d'une justification rigoureuse, j'ai peut-être réduit le degré de catégorisation de certaines des allégations de l'article. Et pourtant ...

Dans ce cas, nous avons 2 lignes de critique.

1) Pourquoi est-ce que je considère 19, 24 ou 29 (etc.) comme inacceptable?

Non, je ne pense pas. Pour différents instruments, il existe des techniques d'utilisation des sons en dehors de l'échelle, par exemple le glissando et le vibrato. Ces techniques ajoutent de la beauté et du naturel au son. Par conséquent, même avec 12 notes, nous utilisons toujours des sons auxiliaires. Si nous parlons d'un environnement, d'un son inhabituel, d'enrichir le son ... alors c'est tout à fait justifié, mais si nous parlons de tonalités de base, alors j'ai des doutes. La musique est créée non seulement pour l'élite, mais pour les gens ordinaires, et pour eux, une telle graduation (IMHO) n'est pas nécessaire.

Le deuxième argument, et il a été donné dans les commentaires, est, en effet, la complexité de la création d'instruments et de performances dans le cas d'une longue échelle, bien que nous ayons un excellent exemple d'un tel instrument - le sitar. Mais essayez de prendre une octave (d'une main) sur le piano si vous avez une échelle de 24 sons.

2) Mais qu'en est-il du pentatonique?

Dans tous les pays de l'Est où je me trouvais, pour une raison quelconque, j'entendais très rarement de la musique nationale construite à l'échelle pentatonique. Et tous les musiciens de l'Est, que j'ai écoutés (et j'adore certains), ont également joué de la musique assez européenne. Voici une citation intéressante: "Les compositeurs universitaires utilisent le pentatonique comme peinture spéciale depuis le 19ème siècle pour donner à la musique une saveur archaïque." L'arôme de l'archaïque ...
Dans ma perception, néanmoins, cette musique n'est pas moderne, mais je ne veux pas défendre cette position, donc à certains endroits dans l'article j'utilise le terme "musique européenne moderne". Il est clair que cette musique (construite sur l'échelle pentatonique) s'est développée selon d'autres lois, et n'a pas atteint la demande de polyphonie riche et de modulation fréquente et facile, qui est apparue dans la musique européenne. Par conséquent, cet article ne concerne évidemment pas la pentatonique.

Critique 3. Musique contemporaine

Comment appeler la musique moderne?

Bien que cela ressemble à une tautologie, par musique moderne, j'entends une musique qui nécessite une invariance, ce qui dans le cas d'instruments avec un système fixe (par exemple, clavecin, piano) conduit à la nécessité d'un système uniformément tempéré (ou quelque chose de proche). Dans le cas d'autres instruments, par exemple les cordes fretless, tout semble un peu plus compliqué, car, en réalité, il est possible d'utiliser un ensemble de sons plus large (que 12). Mais quand nous parlons de l'exigence d'invariance, nous voulons dire que ces sons doivent être très proches (en fréquence) de nos 12.

Cette définition comprend presque toute la musique pour piano, le classique européen, le jazz, la musique rock, la pop et tous leurs dérivés. Je suis sûr qu'il y a des exceptions, mais à mon humble avis, ce sont les exceptions. Je ne vois aucune raison de discuter de cela, car chacun peut investir quelque chose dans ce concept.

Critique 4. Calcul

Erreur dans les calculs.

Je pense que cette question est supprimée. Cependant, je dois admettre qu'au cours de la discussion, j'ai fait plusieurs déclarations erronées sur des questions secondaires qui n'ont pas affecté la conclusion principale de l'article.

PS Ne traitez pas cet article (et faites les exigences correspondantes) comme un travail académique. :) Ce n'est pas un article sur la théorie musicale. De plus, ce n'est pas un article sur l'histoire de la musique. Dans ces domaines, je ne considère en aucune façon mes connaissances comme étant en quelque sorte significatives et j'admets qu'il puisse y avoir des inexactitudes, bien que j'aie essayé de les éviter. On formule ici un problème mathématique simple (de complexité scolaire), dont la solution, me semble-t-il, a une interprétation intéressante. Avec qui j'ai partagé.

Le nombre sous-jacent à la musique moderne