Inférence variationnelle - qu'est-ce que c'est et que mange-t-elle?

Bonjour, Habr!

Récemment, j'ai parlé avec des collègues d'un auto-encodeur variationnel et il s'est avéré que beaucoup même ceux qui travaillent dans le Deep Learning connaissent l'inférence variationnelle (Inférence variationnelle) et, en particulier, la limite variationnelle inférieure uniquement par ouï-dire et ne comprennent pas complètement de quoi il s'agit.
Dans cet article, je souhaite analyser ces problèmes en détail. Peu importe, je demande une coupe - ce sera très intéressant.

Qu'est-ce que l'inférence variationnelle?

La famille des méthodes variationnelles d'apprentissage automatique tire son nom de la section d'analyse mathématique «Calcul variationnel». Dans cette section, nous étudions les problèmes de recherche d'extrêmes de fonctionnels (une fonctionnelle est une fonction de fonctions - c'est-à-dire que nous ne recherchons pas les valeurs de variables dans lesquelles la fonction atteint son maximum (minimum), mais une telle fonction dans laquelle la fonctionnelle atteint un maximum (minimum).

Mais la question se pose - en apprentissage automatique, on cherche toujours un point dans l'espace des paramètres (variables) dans lequel la fonction de perte a une valeur minimale. Autrement dit, c'est la tâche de l'analyse mathématique classique, et voici le calcul des variations? Le calcul des variations apparaît au moment où l'on transforme la fonction de perte en une autre fonction de perte (souvent c'est la limite variationnelle inférieure) en utilisant les méthodes de calcul des variations.

Pourquoi en avons-nous besoin? N'est-il pas possible d'optimiser directement la fonction de perte? Nous avons besoin de ces méthodes lorsqu'il est impossible d'obtenir directement une estimation de gradient sans biais (ou que cette estimation a une dispersion très élevée). Par exemple, nos jeux de modèles $$$p (z)$ et $$$p (x / z)$ , et nous devons calculer $$$p (x) = \ int (p (z) p (x / z) dz)$ . C'est exactement pour cela que l'encodeur automatique variationnel a été conçu.

Qu'est-ce que la limite inférieure variationnelle?

Imaginez que nous ayons une fonction $$$f (x)$ . La limite inférieure de cette fonction sera n'importe quelle fonction $$$g (x)$ satisfaisant l'équation:

$$

$$g (x) <= f (x)$$

Autrement dit, pour toute fonction, il existe d'innombrables limites inférieures. Toutes ces bornes inférieures sont-elles les mêmes? Bien sûr que non. Nous introduisons un autre concept - la divergence (je n'ai pas trouvé de terme établi dans la littérature en langue russe, cette valeur est appelée étanchéité dans les articles en anglais):

$$

$$\ delta = max {f (x)} - max {g (x)}$$

De toute évidence, le résidu est toujours positif. Plus le résidu est petit, mieux c'est.

Voici un exemple de borne inférieure avec zéro résiduel:

Et voici un exemple avec un résiduel petit mais positif:

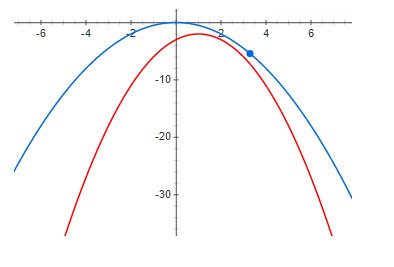
Et enfin, un écart assez important:


D'après les graphiques ci-dessus, on voit clairement qu'à zéro résiduel, le maximum de la fonction et le maximum de la limite inférieure sont au même point. Autrement dit, si nous voulons trouver le maximum d'une fonction, nous pouvons rechercher le maximum de la limite inférieure. Si l'écart n'est pas nul, ce n'est pas le cas. Et le maximum de la limite inférieure peut être très éloigné (le long de l'axe x) du maximum souhaité. Les graphiques montrent que plus le résidu est grand, plus les aigus peuvent être éloignés les uns des autres. Ce n'est généralement pas vrai, mais dans la plupart des cas pratiques, cette intuition fonctionne très bien.

Encodeur automatique variable

Nous allons maintenant analyser un exemple d'une très bonne limite variationnelle inférieure avec un résidu potentiellement nul (ci-dessous, il sera clair pourquoi) - il s'agit d'un autoencodeur variationnel.

Notre tâche est de construire un modèle génératif et de le former en utilisant la méthode du maximum de vraisemblance. Le modèle aura la forme suivante:

$$

$$q (x) = \ int {q (z) q_ \ thêta (x | z) dz}$$

où $$$q (x)$ Est la densité de probabilité des échantillons générés, $$$z$ - variables latentes, $$$q (z)$ - la densité de probabilité d'une variable latente (souvent une simple - par exemple, une distribution gaussienne multidimensionnelle avec une attente nulle et une dispersion unitaire - en général, quelque chose que nous pouvons facilement échantillonner), $$$q_ \ thêta (x | z)$ - densité d'échantillon conditionnelle pour une valeur donnée de variables latentes, dans l'autoencodeur variationnel, on sélectionne une densité gaussienne avec attente de mat et dispersion en fonction de z.

Pourquoi pourrions-nous avoir besoin de représenter la densité de données d'une manière si complexe? La réponse est simple - les données ont une fonction de densité très complexe et nous ne pouvons tout simplement pas construire techniquement directement un modèle d'une telle densité. Nous espérons que cette densité complexe pourra être bien approchée en utilisant deux densités plus simples. $$$q (z)$ et $$$q_ \ thêta (x | z)$ .

Nous voulons maximiser la fonction suivante:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

où $$$p (x)$ - densité de probabilité des données. Le principal problème est que la densité $$$q (x)$ (avec des modèles suffisamment flexibles) il n'est pas possible de présenter analytiquement, et en conséquence de former le modèle.

Nous utilisons la formule de Bayes et réécrivons notre fonction comme suit:

$$

$$I = \ int {p (x) log (\ frac {q (z) q (x | z)} {q (z | x)}) dx}$$

Malheureusement $$$q (z / x)$ tout est également difficile à calculer (il est impossible de prendre l'intégrale analytiquement). Mais tout d'abord, nous notons que l'expression sous le logarithme ne dépend pas de z, nous pouvons donc prendre l'attente mathématique du logarithme en z de toute distribution et cela ne changera pas la valeur de la fonction et multipliera et divisera par le logarithme par la même distribution (formellement, nous n'avons qu'une seule condition - cette distribution ne doit disparaître nulle part). En conséquence, nous obtenons:

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {\ phi (z | x)} {q (z | x)})}}$$

notons que, premièrement, le deuxième terme est la divergence KL (ce qui signifie qu'il est toujours positif):

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + \ int {p (x) KL [\ phi (z | x) || q (z | x))] dx}$$

et deuxièmement $$$I$ ne dépend pas de $$$q (z | x)$ pas de $$$\ phi (z | x)$ . Il s'ensuit que,

$$

$$I> = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} = VLB$$

où $$$Vlb$ - La limite variationnelle inférieure (Variational Lower Bound) et atteint son maximum lorsque $$$KL [\ phi (z | x) || q (z | x))] = 0$ - c'est-à-dire que les distributions sont les mêmes.

Positivité et égalité à zéro si et seulement si les distributions coïncident Les divergences KL sont prouvées précisément par des méthodes variationnelles - d'où le nom de limite variationnelle.

Je tiens à noter que l'utilisation d'une borne inférieure variationnelle offre plusieurs avantages. Premièrement, cela nous donne l'opportunité d'optimiser la fonction de perte par des méthodes de gradient (essayez de le faire lorsque l'intégrale n'est pas prise analytiquement) et deuxièmement, il approximera la distribution inverse $$$q (z | x)$ distribution $$$\ phi (z | x)$ - c'est-à-dire que nous pouvons non seulement échantillonner des données, mais aussi échantillonner des variables latentes. Malheureusement, le principal inconvénient est lorsque le modèle de distribution inverse n'est pas flexible, c'est-à-dire lorsque la famille $$$\ phi (z | x)$ ne contient pas $$$q (z | x)$ - le résidu sera positif et égal:

$$

$$\ delta = \ int {p (x) \ underset {\ phi (z | x)} {min} (KL [\ phi (z | x) || q (z | x)]) dx}$$

et cela signifie que le maximum de la limite inférieure et les fonctions de perte ne coïncident probablement pas. Soit dit en passant, l'encodeur automatique variationnel utilisé pour générer des images génère des images trop floues, je pense que c'est simplement à cause du choix d'une famille trop pauvre $$$\ phi (z | x)$ .

Un exemple de résultat moins bon

Nous allons maintenant considérer un exemple où, d'une part, la limite inférieure a toutes les bonnes propriétés (avec un modèle suffisamment flexible, le résidu sera nul), mais à son tour ne donne aucun avantage sur l'utilisation de la fonction de perte d'origine. Je pense que cet exemple est très révélateur et si vous ne faites pas d'analyse théorique, vous pouvez passer beaucoup de temps à essayer de former des modèles qui n'ont aucun sens. Au contraire, les modèles ont du sens, mais si nous pouvons former un tel modèle, alors il est plus facile de choisir $$$q (x)$ de la même famille et utiliser directement le principe du maximum de vraisemblance.

Ainsi, nous considérerons exactement le même modèle génératif que dans le cas d'un encodeur automatique variationnel:

$$

$$q (x) = \ int {q (z) q_ \ thêta (x | z) dz}$$

nous allons nous entraîner avec la même méthode de maximum de vraisemblance:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

Nous espérons toujours que $$$q (x | z)$ Ce sera beaucoup plus "facile" que $$$q (x)$ .
Seulement maintenant, nous écrirons $$$I$ un peu différent:

$$

$$I = \ int {p (x) log (\ int {q (z) q_ \ theta (x | z) dz}) dx}$$

en utilisant la formule de Jensen, nous obtenons:

$$

$$I> = \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz} = VLB$$

C'est précisément à ce moment que la plupart des gens réagissent sans penser que c'est vraiment le résultat final et que vous pouvez former le modèle. C'est vrai, mais regardons la différence:

$$

$$\ delta = \ int {p (x) log (q (x)) dx} - \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz}$$

où (en appliquant deux fois la formule de Bayes):

$$

$$\ delta = \ int {p (x) q (z) log (\ frac {q (x)} {q (x | z)}) dxdz} = \ int {p (x) q (z) log ( \ frac {q (z)} {q (z | x)}) dxdz}$$

il est facile de voir que:

$$

$$\ delta = \ int {p (x) KL [q (z) || q (z | x)] dx}$$

Voyons ce qui se passe si nous augmentons la limite inférieure - le résiduel diminuera. Avec un modèle assez flexible:

$$

$$KL [q (z) || q (z | x)] \ rightarrow0$$

tout semble aller bien - la limite inférieure a un résidu potentiellement nul et avec un modèle assez flexible $$$q (x | z)$ tout devrait fonctionner. Oui, c'est vrai, seuls les lecteurs attentifs peuvent remarquer que zéro résiduel est atteint lorsque $$$x$ et $$$z$ sont des variables aléatoires indépendantes !!! et pour un bon résultat, la «complexité» de la distribution $$$q (x | z)$ ne devrait pas être inférieur à $$$q (x)$ . Autrement dit, la frontière inférieure ne nous donne aucun avantage.

Conclusions

La limite variationnelle inférieure est un excellent outil mathématique qui vous permet d'optimiser approximativement les fonctions «incommodes» pour l'apprentissage. Mais comme tout autre outil, vous devez très bien comprendre ses avantages et ses inconvénients et aussi l'utiliser très soigneusement. Nous avons considéré un très bon exemple - un auto-encodeur variationnel, ainsi qu'un exemple d'une limite inférieure pas très bonne, tandis que les problèmes de cette limite inférieure sont difficiles à voir sans une analyse mathématique détaillée.

J'espère que c'était au moins un peu utile et intéressant.