L'importance des nombres premiers, à la fois dans l'utilisation quotidienne et dans toutes les branches des mathématiques, ne peut pas être surestimée . Nous comptons calmement sur leurs propriétés particulières, en les utilisant comme fondement d'innombrables éléments de notre société, car ils sont une partie indivisible du tissu même de la nature. Les nombres premiers qui résistent à toute factorisation sont souvent appelés «atomes» du monde des mathématiques. Carl Sagan a dit à leur sujet comme ceci:

Le statut des nombres premiers en tant que blocs de construction fondamentaux de tous les nombres, qui sont eux-mêmes les blocs de construction de notre compréhension de l'Univers, est très important.

Dans la nature et dans nos vies, les nombres premiers sont utilisés partout: les cigales y construisent leur cycle de vie, les horlogers les utilisent pour calculer les tics, et dans les moteurs d'avion, avec leur aide, la fréquence des impulsions d'air est équilibrée. Cependant, tous ces domaines d'application s'estompent dans le contexte familier à tout cryptographe: les nombres premiers sont au cœur même de la sécurité informatique moderne, c'est-à-dire qu'ils sont directement responsables de tout protéger. Voir le verrou dans la barre d'adresse du navigateur? Oui, cela signifie qu'une «poignée de main» à deux touches est utilisée, basée sur des nombres premiers. Comment votre carte de crédit est-elle protégée lors de vos achats? Utilisant également la cryptographie basée sur des nombres premiers.

Cependant, malgré le fait que nous comptons constamment sur leurs propriétés uniques, les nombres premiers nous sont restés insaisissables. Tout au long de l'histoire des mathématiques, les plus grands esprits ont essayé de prouver un théorème sur la prédiction de nombres premiers, ou sur la distance à laquelle ils devraient être éloignés les uns des autres. En fait, certains problèmes non résolus, tels que le problème des nombres jumeaux , le problème de Goldbach , les nombres premiers de palindrome et l' hypothèse de Riemann , sont associés à cette imprévisibilité générale et à l'incertitude des nombres premiers lorsqu'ils tendent vers l'infini. Bien sûr, depuis l'époque d'Euclide, nous avons découvert des algorithmes qui nous permettent de prédire l'emplacement de certains nombres, mais les théorèmes généraux n'ont pas encore été prouvés, et les tentatives précédentes n'avaient pas d'outils pour vérifier les grands nombres. Cependant, la technologie du 21e siècle permet aux chercheurs de tester des hypothèses sur des nombres extrêmement élevés, mais cette technique seule est controversée, car un dépistage grossier n'est pas considéré comme une preuve fiable. En d'autres termes, les nombres premiers résistent à obéir à toute formule ou équation universelle, et leur arrangement dans la nature semble aléatoire.

Cependant, une personne avec des gribouillis aléatoires a réussi à prouver qu'ils ne sont au moins pas complètement aléatoires ...

Des gribouillis à une astuce - Nappe Ulam

L'une des plus grandes preuves que l'arrangement des nombres premiers n'est pas une pure coïncidence est apparue de la manière la plus improbable: à partir des griffonnages irréfléchis et aléatoires d'un étudiant ennuyé de conférences.


Nappe Ulam

Au fil de l'histoire, le mathématicien polonais Stanislav Ulam a découvert ce motif graphique lors d'un séminaire en 1963. Dessinant une grille de lignes, il a décidé de numéroter les intersections dans un motif en spirale carrée et a commencé à encercler les nombres en spirales qui étaient simples. À sa grande surprise, les nombres premiers encerclés sont tombés sur des lignes droites diagonales ou, comme Ulam l'a dit un peu plus sévèrement, "ont montré un comportement fortement non aléatoire". La nappe d'Ulam, ou spirale de nombres premiers, est l'affichage graphique résultant de l'ensemble des nombres premiers délimités dans une spirale carrée. La nappe a été initialement publiée et est devenue largement connue sous le titre "Mathematical Games" de Martin Gardner dans Scientific American .


Nappe Ulam mesurant 377x377 (nombres jusqu'à environ 142 mille)

La visualisation ci-dessus révèle évidemment des motifs remarquables, en particulier le long des diagonales. Mais peut-être que nous nous trompons? On prétend souvent que la nappe d'Ulam n'est qu'un tour de notre cerveau essayant de trouver des motifs aléatoires. Heureusement, nous pouvons utiliser deux techniques différentes pour nous assurer que ce n'est pas le cas. La comparaison visuelle et l'analyse logique nous indiquent clairement que le motif n'est pas accidentel. Tout d'abord, nous comparons la nappe Ulam définie par une matrice de taille NxN avec une matrice de même taille contenant des points définis aléatoirement. Deuxièmement, nous pouvons utiliser notre connaissance des polynômes pour comprendre pourquoi nous devrions nous attendre à ce qu'un modèle apparaisse lors de l'affichage graphique des nombres premiers.

Comme mentionné ci-dessus, très probablement, la confirmation la plus intuitive du caractère non aléatoire du motif sera une comparaison directe avec la nappe d'Ulam. Pour ce faire, créez une nappe Ulam et une spirale carrée avec des emplacements aléatoires de même taille. Deux matrices 200x200 différentes représentant des spirales numériques sont présentées ci-dessous:


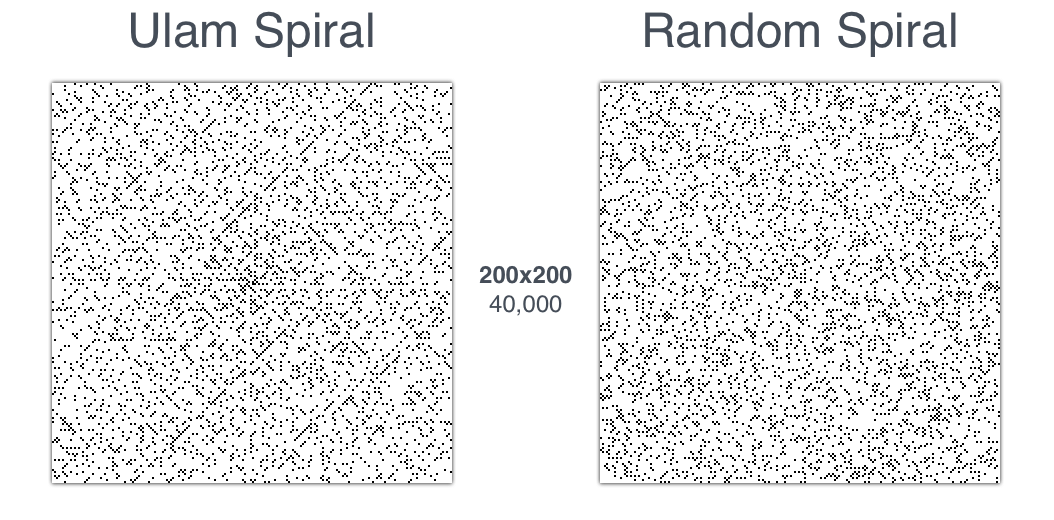
Une comparaison visuelle rend assez évident que la nappe d'Ulam contient des motifs époustouflants, en particulier le long des axes diagonaux; en outre, il ne contient presque pas de groupes de points. En revanche, l'agencement aléatoire des points ne crée pas immédiatement de motifs perceptibles et conduit à l'accumulation de points dans des directions différentes. Sans aucun doute, une telle technique n'a pas la rigueur des preuves traditionnelles; cependant, il y a quelque chose d'impeccable dans la visualisation des spirales de nombres premiers: c'est une technique découverte au hasard qui vous permet de créer un graphique qui stimule la logique et est attrayant esthétiquement.

Si nous abordons la nature des nombres premiers d'une manière plus logique et traditionnelle, il est tout à fait raisonnable de s'attendre à l'apparition de motifs dans de telles visualisations. Comme indiqué ci-dessus, les lignes dans les directions diagonales, horizontales et verticales semblent contenir un indice. Certaines de ces lignes, qui ne sont pas des nombres premiers, peuvent être expliquées par des polynômes carrés ordinaires qui excluent la possibilité de l'apparition de nombres premiers - par exemple, l'une des lignes diagonales correspondant à l'équation y = x² exclut évidemment les nombres premiers. D'autre part, on sait que certains polynômes carrés, appelés formules premières (nous en parlerons ci-dessous), créent une forte densité de nombres premiers, par exemple, le polynôme premier d'Euler: x² - x - 41; c'est une autre ligne reflétée comme un motif dans une spirale (bien qu'il soit difficile de trouver des lacunes dans le diagramme ci-dessus).

Une comparaison visuelle indique des modèles et une analyse logique confirme l'existence des modèles attendus. Bien sûr, nous sommes encore loin d’une formule universelle pour trouver tous les nombres premiers, mais la nappe d’Ulam est sans aucun doute belle, à la fois comme symbole de nos connaissances et comme chef-d’œuvre de l’art naturel.

Spirale Sachs

Comme dans de nombreux domaines des mathématiques, après l'avènement de l'idée originale, l'armée de collègues mathématiciens qui ont suivi les traces a commencé à tenter de contribuer au nouveau sujet. Il est logique que la nappe d'Ulam ait inspiré des générations de mathématiciens qui ont cherché à développer son incroyable trouvaille. En 1994, l'ingénieur logiciel Robert Sachs a décidé d'utiliser ses compétences en programmation pour visualiser les nombres premiers de diverses manières.

Presque comme dans le cas de la nappe d'Ulam, Sachs a décidé de structurer son schéma en utilisant un autre plan en spirale. Semblable à la spirale carrée illustrée ci-dessus, les plans en spirale refusent de donner des points au système numérique cartésien traditionnel, car ils sont un système de positionnement unipolaire . En connaissant simplement le nombre, vous pouvez découvrir son emplacement dans la spirale, sa position par rapport à tous les autres nombres dans la spirale, ainsi que la distance de celui-ci au carré précédent et suivant du nombre. Cependant, au lieu d'une spirale carrée, Sax a essayé de trouver des modèles à l'aide d'entiers superposés à une spirale d'Archimède avec les coordonnées polaires suivantes:


Coordonnées polaires de la spirale d'Archimède / Sachs

Avec cette technique, la spirale archimédienne est centrée autour de zéro, et les carrés de tous les nombres naturels (1,4,9,16,25) sont situés aux intersections de la spirale et de l'axe polaire (situé à l'est de l'origine).


Structure en spirale Archimède / Sax

Après avoir préparé ce diagramme, nous remplirons les points entre les carrés le long de la spirale (dans le sens antihoraire), en les appliquant à une distance égale les uns des autres. Et au final, comme dans l'exemple avec la nappe d'Ulam, nous distinguerons les nombres premiers contenus dans la spirale résultante.

La spirale numérique Sachs, publiée pour la première fois en ligne en 2003, est attrayante à la fois visuellement et intellectuellement. De plus, comme nous le verrons bientôt, elle nous donne une compréhension plus profonde des motifs premiers que la nappe Ulam bien connue, car elle combine les lignes brisées de la pseudo- spirale Ulam :


Spirale archimédienne aux nombres premiers marqués, c'est aussi la spirale saxonne.

Le graphique résultant montre à nouveau des modèles perceptibles. Presque immédiatement, il devient clair qu'il existe une ligne blanche propre allant du centre et s'étendant horizontalement vers l'est. En ce qui concerne notre schéma, nous pouvons nous assurer qu'il ne s'agit que d'une ligne contenant tous les carrés d'entiers (r = n ^ (. 5)). Deuxième constat: le motif de marquage, contrairement aux lignes droites de la nappe Ulam, ressemble plus à des lignes courbes . Il s'avère que ces courbes, également connues sous le nom de courbes de produits , nous renvoient à des polynômes expliquant les motifs qui se produisent dans la spirale précédente. Mais avant de nous tourner vers eux, par souci d'unité, nous comparons à nouveau la spirale de Sachs avec la spirale de valeurs aléatoires:

Polynômes et courbes de produits

Le travail de Robert Sachs à la suite de cette découverte s'est entièrement concentré sur ces pièces tordues , commençant au centre de la spirale ou près de celle-ci, et se croisant à différents angles avec les spires de la spirale. Les courbes sont presque droites, mais plus typiques pour elles, c'est qu'elles effectuent des rotations partielles, complètes ou multiples dans le sens des aiguilles d'une montre (contre le mouvement de la spirale elle-même) autour de l'origine, avant d' être redressées à un certain décalage par rapport à l'axe est-ouest. L'un des aspects les plus frappants de la spirale numérique de Sachs est la prédominance de ces œuvres courbes dans l'hémisphère occidental (du côté opposé au carré des nombres).

Sachs a décrit les courbes de produits comme représentant des «produits de facteurs avec une différence constante entre eux». En d'autres termes, chaque courbe peut être représentée par une équation quadratique (polynôme du deuxième degré), qui n'est pas encore une simple coïncidence, étant donné la prévalence du carré d'un nombre naturel dans la spirale de Sachs. Ces courbes de produits peuvent peut-être nous conduire à la conclusion que la spirale de Sachs est beaucoup plus utile dans notre chemin vers la compréhension des nombres premiers que la nappe d'Ulam. Bien que la nappe d'Ulam nous ait montré les motifs et l'existence possible d'équations, la spirale de Sachs fournit des points d'appui dans la recherche de formules premières - leur courbure et leur intégrité sont constantes, ce qui signifie qu'elles seront beaucoup plus faciles à détecter. Par exemple, la spirale Sachs illustrée ci-dessous contient des lignes étiquetées et leur formule principale correspondante, écrites sous forme standard. Comme je l'ai promis, la fameuse formule d'Euler pour générer des nombres premiers nous a de nouveau rencontrés (dernière entrée: n² + n +41):


Grâce à cette spirale numérique, Sax a pu faire une déclaration étonnante sur ce qu'est un nombre premier: un entier positif qui se trouve sur une seule courbe du produit. Étant donné que la spirale peut tourner sans fin, les courbes elles-mêmes peuvent également être considérées comme infinies; théoriquement, ces courbes de produits peuvent éventuellement prédire l'emplacement de nombres suffisamment grands - au moins ces nombres méritent un examen plus approfondi.

Dans l'ensemble, la spirale de Sachs nous a sans aucun doute incités à une compréhension plus profonde des nombres premiers en proposant des formules plus pratiques pour les nombres premiers.

Signification de tout

Nous avons donc analysé à la fois la nappe d'Ulam et la spirale Sax. Grâce à ces exemples, notre compréhension de la nature des nombres premiers s'est élargie. En particulier, la spirale de Sachs nous a présenté les courbes de produits, qui sont essentiellement un ensemble d'équations quadratiques, appelées formules premières. Les deux graphiques, Ulama et Sax, se sont révélés inattendus et esthétiques, ils stimulent notre curiosité et éclairent l'une des tâches les plus difficiles pour le monde entier.

Quelle leçon peut-on tirer de tout cela?

Vous ne pouvez jamais refuser d'examiner des problèmes apparemment insolubles, même si vous le faites par pure curiosité et ennui; tout le monde peut faire des découvertes et elles surviennent souvent à la suite de processus complètement inhabituels. Ayant changé son point de vue sur la fameuse tâche grâce à la visualisation, Stanislav Ulam nous a rapprochés de la compréhension des nombres premiers: qui sait quelles autres découvertes inattendues nous rencontrerons?