Formule de calcul des nombres premiers et d'optimisation des diviseurs de force brute

Salutations! J'ai décidé à loisir de rechercher le problème de la recherche des nombres premiers. Le sujet est vaste et intéressant. Je veux partager quelques réflexions à ce sujet qui me sont venues à l'esprit. Une recherche sur Internet n'a pas révélé de tels éléments, soulignant leur originalité.

Premièrement, je n'ai jamais trouvé de formule mathématique pour calculer l'ordre des nombres premiers. Mais après tout, s'il existe des algorithmes, il est certainement possible de composer des formules à l'aide de fonctions logiques ou d'opérateurs. Je donne ci-dessous la formule la plus concise qui s'est avérée.

Pour une séquence de nombres $$$(x_ {m}) = {x_ {1}, x_ {2}, x_ {3}, ... x_ {max}}$ on introduit l'opérateur de détection du premier nombre égal à a:

$$

$$\ mathbf {Dt_ {a}} (x_ {m}): = \ left \ {\ begin {matrice} m \ \ mathbf {if} \ \ existe \ m: \ forall \, k <m \ x_ {k } \ neq a \ \ mathbf {et} \ x_ {m} = a \\ 0 \ \ mathbf {sinon} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ end {matrix} \ right.$$

Tous les nombres premiers, commençant par 5, peuvent être calculés par la formule:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1} + 2i) \, mod \, P_ {j + 1})), \ \ \ \ forall \, n \ geqslant 3 \\ \ forall \, i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ alpha -1}} {2} +10 \ ,, \ \ 2 \ leqslant \ alpha \ leqslant n-1; \ \ j_ {max} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1$$

Opératrice $$$\ mathbf {Dt_ {0} ^ {j}}$ itère sur $$$j$ le reste de la division de chaque numéro de candidat par simplicité avec $$$i$ nombre $$$(P_ {n-1} + 2i)$ aux nombres premiers déjà trouvés dans la gamme jusqu'à $$$P_ {j_ {max} +1}$ . Les numéros des candidats sont sélectionnés dans l'ordre parmi l'ensemble des nombres impairs supérieurs au nombre premier précédent $$$P_ {n-1}$ . $$$\ pi (\ sqrt {P_ {n-1} + 2i})$ Est une fonction pi montrant le nombre de nombres premiers $$$\ leqslant \ sqrt {P_ {n-1} + 2i}$ .
Opératrice $$$\ mathbf {Dt_ {0} ^ {i}}$ itère sur $$$i$ valeurs de sortie de l'opérateur $$$\ mathbf {Dt_ {0} ^ {j}}$ jusqu'à ce qu'il trouve 0. Puisque la série de nombres premiers est infinie, cela se produira tôt ou tard. A la sortie de l'opérateur $$$\ mathbf {Dt_ {0} ^ {i}}$ donc il y aura toujours un certain nombre $$$i$ . Limite inférieure $$$i_ {max}$ est déterminé par la différence maximale de nombres premiers adjacents inférieurs à celui souhaité. L'augmentation de cette différence se produit logarithmiquement. Le graphique ci-dessous montre la dépendance de la croissance maximale et moyenne $$$\ Delta P _ {\ alpha}$ à partir de n pour les 100 000 premiers nombres premiers. La valeur maximale a été échantillonnée et moyenne pour chaque millier de nombres.
L'augmentation maximale de la différence des nombres premiers $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ à la valeur maximale précédente $$$max (\ Delta P _ {\ alpha})$ égal à 20 (pour la différence des nombres premiers 31397-31469 = 72 par rapport à la différence 25523-25471 = 52). C'est dans la région où la dérivée du logarithme de l'enveloppe $$$\ Delta P _ {\ alpha}$ encore assez grand, et les nombres premiers ne sont plus trop petits. Sur la base de cette valeur, la condition pour $$$i_ {max}$ . Graphique $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ pour les 50 000 premiers nombres premiers indiqués ci-dessous. Les valeurs ont été calculées pour chaque millier.
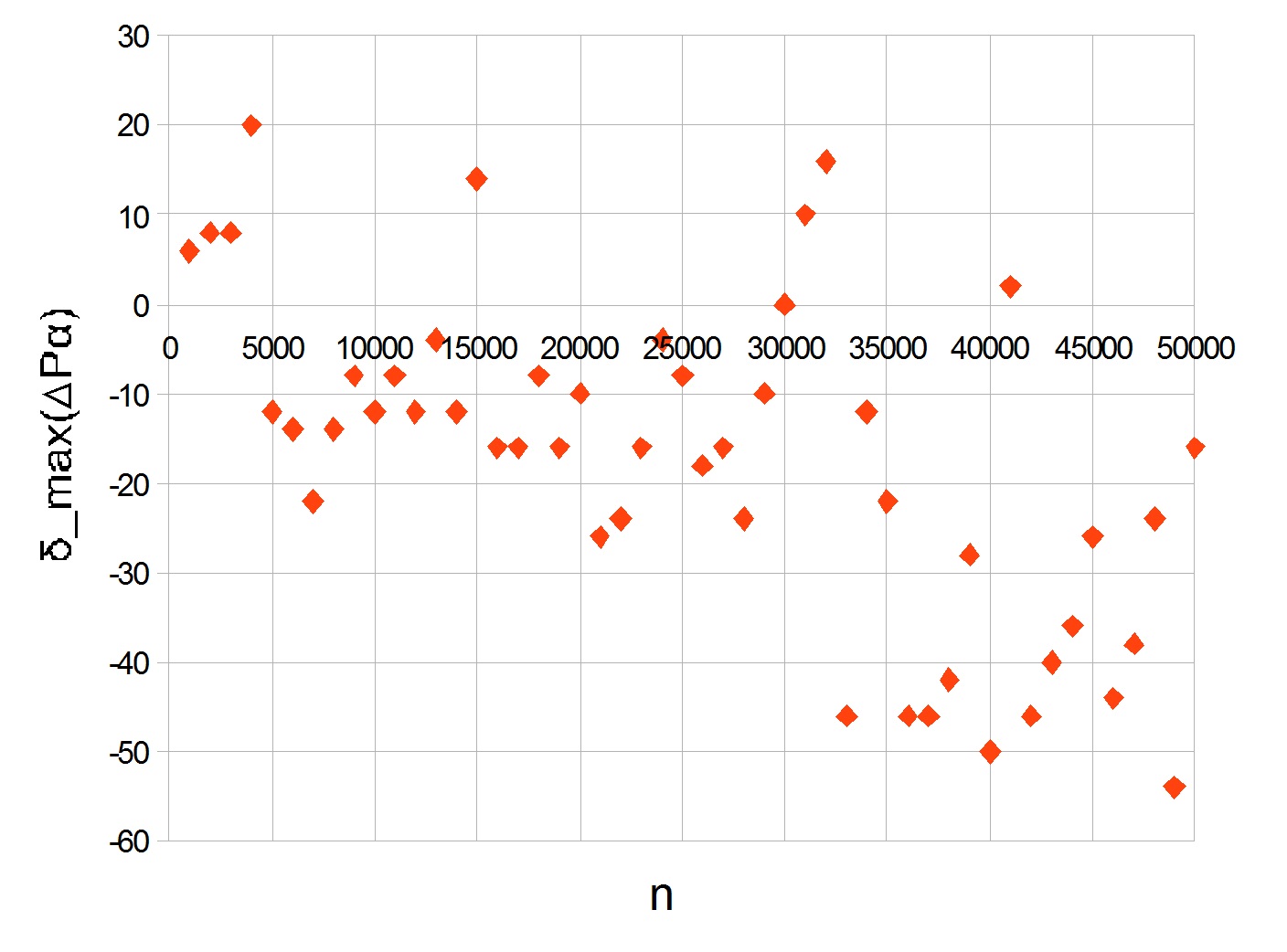
Le pic est visible à 20. Avec l'augmentation de n, le graphique passe à moins, montrant une diminution du taux de croissance des grands nombres premiers.

La deuxième considération est d'optimiser le calcul d'une séquence de nombres premiers.
L'algorithme présenté dans la formule ci-dessus est une méthode améliorée pour énumérer les diviseurs. Les améliorations consistent à exclure les nombres pairs de la considération et à vérifier la divisibilité des nombres premiers uniquement inférieurs à sq. les racines des numéros des candidats. La partie la plus difficile de l'algorithme est le calcul de l'ensemble des fonctions mod restantes. La complexité peut être réduite en optimisant cette fonction. Cependant, il existe un moyen encore plus efficace. Soit $$$(r_ {j + 1} ^ {n-1}) = {r_ {2}, r_ {3}, ... r _ {\ pi (\ sqrt {P_ {n-1}})}}$ Est une séquence de résidus de la division du dernier nombre premier trouvé en nombres premiers de 3 à la racine de celui-ci. Nous allons faire des séquences du formulaire

$$

$$(r_ {i, j + 1} ^ {n}) = {(r_ {2} + 2i) \, mod \, P_2, (r_ {3} + 2i) \, mod \, P_3, ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1}})}, (P_ {n -1} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1} + 2i})}}$$

dans l'ordre à partir de $$$i = 1$ . Le dernier terme est calculé si $$$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ . Quand à une étape du calcul, le reste $$$r_ {i, j + 1} ^ {n}$ devient égal à 0, passez à la séquence suivante. Cela se fait jusqu'à ce que l'on trouve i , où tous les résidus sont non nuls. Cela signifie trouver le prochain nombre premier. Séquence $$$(r_ {j + 1} ^ {n})$ il doit être enregistré jusqu'à ce que le prochain nombre premier soit trouvé. La formule récurrente pour calculer les nombres premiers de cette manière est convertie en:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} (r_ {i, j + 1} ^ {{ n})), \ \ \ \ forall \, n \ geqslant 3$$

Dans l'algorithme présenté, le mode de fonctionnement est facilité: divisible par $$$(r_ {j + 1} + 2i) / P_ {j + 1}$ fois plus de séparateurs. Les seules exceptions sont l'apparition de nouveaux diviseurs simples. En mémoire informatique, lors de la mise en œuvre de l'algorithme, il est nécessaire de stocker un tableau de nombres premiers à la racine du recherché, ainsi qu'un tableau variable de résidus. La complexité de l'algorithme au sens général (la quantité de travail) peut être inférieure à celle des autres méthodes connues. Les opérations les plus complexes sont l'extraction de la racine carrée, le calcul des résidus et la multiplication. La racine peut être extraite à l'entier le plus proche. Pour obtenir des résidus, vous pouvez utiliser un algorithme efficace basé sur la règle générale de divisibilité. La multiplication n'est utilisée que par 2 nombres relativement petits i . La complexité temporelle de l'algorithme peut être réduite en répartissant le travail selon les valeurs de i . Le tamis segmenté obtenu de cette manière devrait fonctionner plus rapidement sur les ordinateurs multithreads. Cependant, le travail effectué sera plus important en raison de l'augmentation des dividendes. Vous pouvez également «visser» la factorisation des roues sur l'algorithme. Avec la taille optimale des roues, cela peut réduire la complexité dans une certaine plage de n - jusqu'à ce que le matériel "wilds" le ralentisse.

Peut-être que quelqu'un viendra en aide à mes pensées.