La justification mathématique de l'inopportunité de descendre l'escalier mécanique dans le métro

Contrairement aux règles d'utilisation du métro, afin de gagner du temps, chacun de nous a couru au moins une fois dans sa vie dans l'escalator. À première vue, il semble que cela soit absolument logique et correct: si vous voulez partir plus vite - essayez d'être sur la plateforme le plus tôt possible. Cependant, presque immédiatement, le scénario suivant vient à l'esprit: vous descendez l'escalier mécanique, descendez vers la plate-forme et les portes de la voiture se ferment juste devant votre nez. Pendant que vous attendez le prochain train - les gens qui sont montés sur l'escalator en même temps que vous avez le temps de vous arrêter tranquillement descendent et prennent le prochain train. Dans ce cas, il n'y a pas de gain. Alors, comment est-il rationnel de descendre l'escalier mécanique et cela vaut-il la peine de le faire? Je m'empresse de vous faire plaisir - la réponse est trouvée! Ci-dessous se trouve une justification mathématique de l'inexpérience (oui, ce n'est PAS) de descendre l'escalier mécanique dans le métro.

Énoncé de tâche

Avant de passer au raisonnement mathématique, il convient de mentionner que, naturellement, je ne suis pas le premier à réfléchir à cette question. Sur Internet, vous pouvez trouver un nombre suffisant d'articles et même des actualités des chaînes fédérales sur ce sujet. Cependant, à chaque fois, l'essence de telles expériences réside dans la descente habituelle de l'escalator avec la comparaison ultérieure du temps gagné avec le temps de la personne debout sur l'escalator. Un peu mieux si les auteurs tentent d'évaluer l'efficacité de la descente. Encore mieux s'ils fournissent toujours des statistiques. Pour les statistiques, en passant, je dirai un merci spécial un peu plus bas. En lien avec le manque de clarté de ces expériences et le manque de conclusions pratiques, j'ai été conçu, puis réalisé, une analyse du processus en cours.

Et donc, nous formulons les conditions du problème et désignons les restrictions:

1. L'expérience (mentale) implique deux personnes qui s'approchent de l'escalator en même temps à un moment aléatoire et n'ont aucune idée de l'endroit où se trouve le train.
2. L'une de ces personnes est debout sur un escalator et passe du temps dans une descente. $$ égal au temps de mouvement de l'escalier mécanique.
3. Le second accélère vers le bas de l'escalator, augmentant sa vitesse $$ fois, réduisant ainsi le temps de descente du même nombre de fois: $$ .
4. Une descente accélérée est considérée comme efficace , ce qui a conduit à ce que la personne debout sur l'escalator n'a pas le temps de monter dans le train, dans laquelle la personne qui s'échappe sur l'escalator a le temps de monter à bord.
5. Désigner par $$ - la probabilité d'une descente effective. Ensuite, selon l'équilibre de Nash, une personne n'est prête à tenter sa chance et à descendre l'escalier mécanique que si la probabilité d'une descente effective est supérieure ou égale à la probabilité d'une descente ou d'un arrêt inefficace en place, soit 0,5. Si la probabilité d'une descente effective est supérieure ou égale à 0,5, la décision de descendre l'escalier mécanique sera jugée appropriée . Si moins de 0,5 - impossible .
6. Nous négligeons le fait que dans la vraie vie, en règle générale, il est nécessaire d'aller plus loin jusqu'à la voiture après avoir quitté l'escalator ou d'attendre que les gens la quittent, les trains circulent à intervalles variables et restent un certain temps immobiles avant d'ouvrir et après avoir fermé les portes, c'est-à-dire que nous supposerons que si au moment de quitter l'escalier mécanique le train est à la gare, alors ses portes sont ouvertes et le participant à l'expérience se retrouve instantanément dans la voiture, le train lui-même ouvre (ferme) les portes et arrive (part) à la gare (de la gare) instantanément et dnomomentno.

Progression de la décision

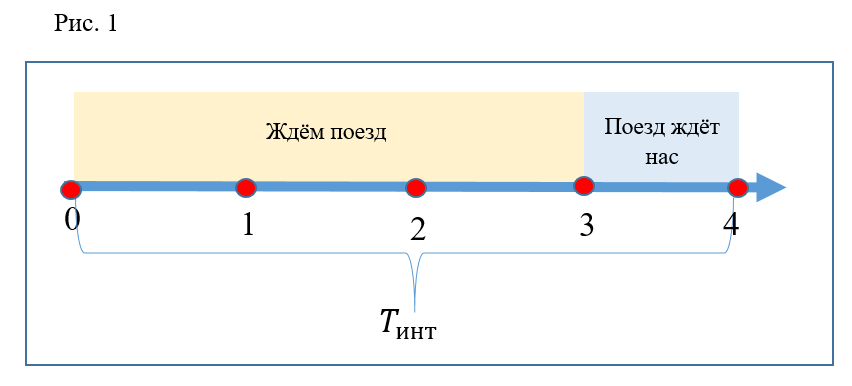
Dessinons l'axe du temps (Fig.1). L'axe entier sera des intervalles consécutifs entre les trains. Ci-après, un seul intervalle sera pris en compte. Divisez l'intervalle indiqué en 4 segments égaux. Le point 0 sur cet axe correspond au moment où le train quitte la gare. Le point 3 correspond à l'arrivée du train et à l'ouverture des portes. Point 4 - fermeture des portes et départ du train. Ainsi, pour la commodité de la représentation graphique et des calculs, l'intervalle entre les trains est compté entre les instants de départ des trains de la gare. Les 3 premiers segments sont le temps que les passagers sont obligés d'attendre pour le train qui arrive. Le quatrième segment est le temps d’arrêt du train, lorsque les passagers peuvent monter à bord. Mettez aussi ce temps $$ (temps de descente sur l'escalator) est égal à deux segments. Coefficient $$ égal à 2, c'est-à-dire le temps de descente courant 2 fois moins et égal à un segment.



Maintenant, pour déterminer la probabilité $$ , découvrez dans quelle période la décision de faire du jogging conduira au fait que la descente sera effective. Par exemple, si nos participants s'approchent de l'escalator au temps 0, alors le premier sera sur la plate-forme au moment $$ (Fig.2), et la seconde plus tôt, en ce moment $$ . Mais, comme on peut le voir sur la figure, à aucun de ces moments, il n'y a un train à la gare, ce qui signifie que la descente était inefficace.



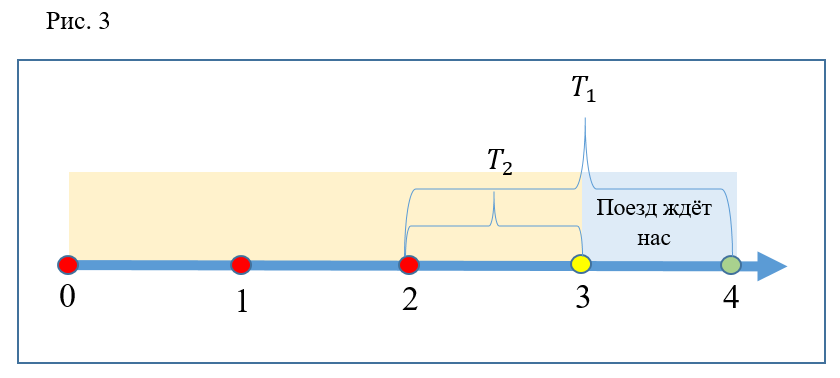
Prenons un autre cas (Fig. 3): les participants à l'expérience s'approchent de l'escalator au temps 2. Comme dans le cas précédent, le premier sera sur la plate-forme au moment $$ , et la seconde plus tôt, en ce moment $$ . Mais il est évident qu'à chaque fois le train est à la gare. Ainsi, les deux auront le temps de monter à bord du même train, donc la descente était tout aussi inefficace.



De plus, il est facile de comprendre qu'à tout moment dans l'intervalle de 2 à 3, la descente est efficace, car la personne évadée parvient toujours à monter à bord du train, et non celle qui s'est échappée. Si vous choisissez des points horaires entre 3 et 4, les deux participants sont en retard pour le train et sont obligés d'attendre le prochain ensemble, c'est-à-dire que courir à nouveau est inefficace.

Il s'avère que sur 4 périodes conventionnelles, il n'est efficace de descendre que si les participants s'approchent de l'escalator entre 2 et 3 fois (Fig. 4). La probabilité d'y entrer est de 1/4. Par conséquent, dans les conditions données de la tâche, il est impossible de prendre une décision de délabrement, car le deuxième participant est plus susceptible (avec une probabilité de 3/4) de courir en vain et sera obligé d'attendre le train avec le premier, qui est descendu plus tard.



Les remarques suivantes seront parfaitement justes:

1. Les intervalles entre les trains peuvent à la fois diminuer et augmenter. Le temps de stationnement peut augmenter et le temps d'attente peut diminuer (avec le même intervalle) et vice versa.
2. La vitesse de descente de l'escalator est constante, mais le temps de descente peut varier, car les stations peuvent être plus ou moins profondes.
3. Le deuxième participant pourrait bien courir non pas 2, mais 3 ou même 4 fois plus vite que l'escalator.

Pour évaluer l'impact des changements dans les facteurs ci-dessus, il est nécessaire de dériver la relation entre ces valeurs et la probabilité de monter sur l'escalator à un moment où il est efficace de s'épuiser.

Pour ce faire, nous allons décrire un autre cas (Fig. 5). Nous laissons toutes les données originales inchangées à l'exception d'une: coefficient $$ augmenter à 4. Autrement dit, le deuxième participant sera au fond 4 fois plus rapide que le premier. Pour la commodité de l'image, nous divisons notre intervalle en 8 parties égales. Ainsi, le temps de descente sur l'escalator est désormais égal à 4 segments, le train s'arrête à deux, le temps d'attente est de 6 et le temps de descente pour rouler seul. Il n'est pas difficile de découvrir que maintenant la durée de l'intervalle de temps «effectif» (de 4 à 7 points dans le temps) est de 3. C'est-à-dire la probabilité $$ égal à 3/8. C'est déjà plus que dans le premier cas, mais nous n'avons pas du tout effectué ces changements pour évaluer la probabilité.



Sur la base des figures 4 et 5, il est évident que la longueur du segment «effectif» est $$ . Divisez-le par la longueur de l'intervalle et obtenez la probabilité $$ où $$ .
Nous effectuons une série de transformations: $$$$ .
La formule finale: $$ .

Sur la base de cette formule, plusieurs conclusions fondamentales peuvent être tirées à la fois:

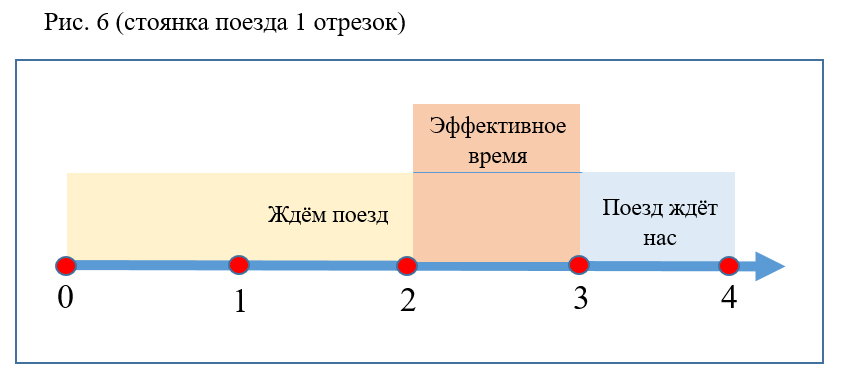
1. La valeur de probabilité n'est pas affectée par les changements dans le temps de stationnement et le temps d'attente du train si l'intervalle total ne change pas (Fig. 6).
   
   
   
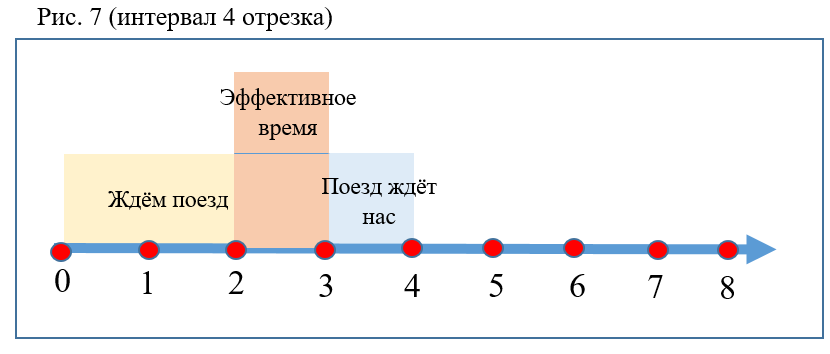
2. Plus l'intervalle entre les trains est grand, plus la probabilité P est faible (Fig. 7).
   
   
   
3. La probabilité augmente si le rapport du temps de descente sur l'escalator à l'intervalle et / ou au coefficient K augmente.
   

Chèque de fidélité

Voyons maintenant à quel point la formule dérivée est vraie?

Pour vérifier l'exactitude de la formule, nous nous tournons vers les statistiques, qui étaient très utiles en 2014 par le correspondant du Village. J'exprime ma reconnaissance et, naturellement, à la fin de l'article je laisserai un lien vers l'article d'origine. Il est également bon que les statistiques soient présentées sous forme d'infographies visuelles.

Expérience 1. Station de métro Chekhovskaya



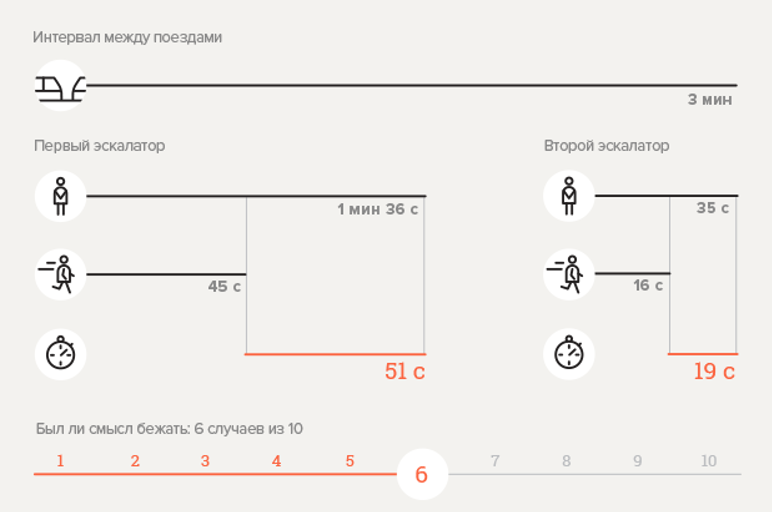
Calculez la probabilité $$ .
Ici $$ ; $$ ; $$ ; $$ ; $$ .

Le résultat obtenu, apparemment, diverge des données expérimentales. La formule est-elle mauvaise? Non! L'infographie montre que la descente vers la gare implique un trajet sur deux escaliers mécaniques, cependant, le temps de transition entre eux n'est pas pris en compte. Si, pour plus de fiabilité, nous supposons que la transition prend au moins 30 secondes, alors, en remplaçant une nouvelle valeur $$ nous obtenons: $$ ; $$ , qui est beaucoup plus proche du résultat expérimental. Il convient également de noter que l'expérience ne prévoyait que 10 répétitions. En augmentant le nombre de répétitions, il est possible d'obtenir une coïncidence presque complète des données calculées avec les résultats obtenus pendant l'expérience.

Expérience 2. Station de métro "Victory Park"



Calculez la probabilité $$ .
Ici $$ ; $$ ; $$ ; $$ ; $$ .
On peut voir que nous avons obtenu une probabilité supérieure à un. Mais il n'y a pas de contradiction ici. Si vous regardez la forme générale de la formule, il devient évident que dans le cas où le temps de descente sur l'escalator est égal à l'intervalle entre les trains, une augmentation de la vitesse d'au moins 2 fois rendra la probabilité qu'une descente accélérée soit effective égale à 0,5. Si le temps de trajet de l'escalator est supérieur à l'intervalle, alors avec le même coefficient $$ la probabilité d'attraper un train plus tôt ne fera qu'augmenter. Enfin, si le temps de descente sur l'escalator est 2 fois ou plus l'intervalle, la personne qui court dans 100% des cas sera à l'heure pour le train que le reste de l'escalator n'aura pas le temps. C'est cet effet que nous observons dans cette expérience: le correspondant a conclu qu'il s'était emporté dans 10 cas sur 10.

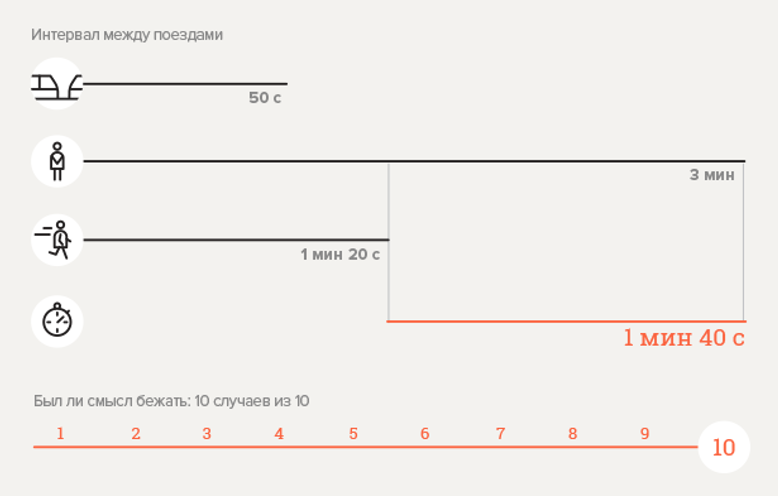
Expérience 3. Station de métro Park Kultury



Calculez la probabilité $$ .
Ici $$ ; $$ ; $$ ; $$ ; $$ .

Encore une erreur? Pas du tout. On peut voir que, comme indiqué ci-dessus, le temps de descente sur l'escalator est 2 fois l'intervalle entre les trains. Le temps de course est 2 fois moins long. Il s'avère que chaque descente doit être efficace. Mais n'oubliez pas qu'avant d'entamer la discussion, nous avons fait l'hypothèse concernant la fermeture instantanée des portes et au moins le départ instantané du train de la gare. Si vous imaginez une telle option comme dans la figure 8, il devient clair que dans la vie réelle, une personne fugueuse peut ne pas avoir le temps de s'asseoir au point 1 (par exemple, le train partira un peu plus tôt) et au point 2, le train, au contraire, retardera un peu, puis une personne qui ne court pas s’asseoira avec une personne qui courra tard dans le train précédent.



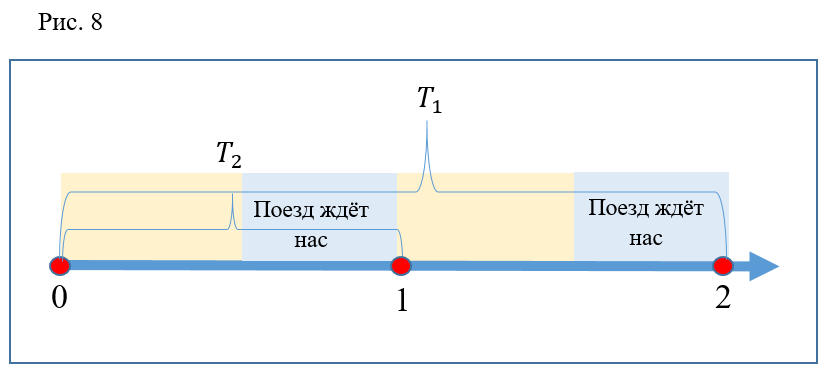
Je suppose que dans les deux temps «inefficaces», cela s'est produit. Il y a tout lieu de penser qu'avec une augmentation du nombre de répétitions de l'expérience, le pourcentage de cycles "efficaces" tendra à 100%.

Conclusions

Maintenant que, sur la base des données expérimentales disponibles, il a été possible de confirmer l'exactitude de la formule, nous allons l'analyser et tirer des conclusions. Étant donné qu'au tout début, nous avons convenu que nous envisagerions la décision de courir vers le bas si la probabilité d'une descente effective est supérieure ou égale à 0,5. C'est littéralement, si nous pouvons être sûrs que dans au moins la moitié des cas, nous courrons pour une bonne raison, alors cela vaut vraiment la peine de prendre le risque et de courir, parce que si nous sommes en retard, nous ne perdrons pratiquement rien. Sur la base de ce qui précède, nous réécrivons la formule de probabilité comme suit: $$ .

Il est intéressant de noter que, comme nous l'avons déjà découvert, il est logique de toujours $$ . Dans le même temps, il est également vrai que si $$ , quelle que soit la vitesse à laquelle vous courez, la probabilité de monter plus tôt dans un train est inférieure à 0,5, car il est évident que $$ ne sera jamais supérieur ou égal à 1.

Voyons maintenant la vitesse du correspondant. En moyenne, c'est environ 2 fois la vitesse de l'escalator (le temps de descente est 2 fois moins). En général, ces données coïncident avec les résultats de mes propres expériences (je ne vois pas l'intérêt de les apporter). En règle générale, il est déjà difficile de développer une vitesse avec un coefficient K d'au moins 3: il y a beaucoup de gens qui veulent descendre en bas sur un véritable escalator et, de plus, les gens debout à gauche ou leurs affaires (sacs, valises) peuvent interférer. Moyens $$ et $$ . Autrement dit, une décision d'accélération ne sera appropriée que si le rapport $$ pas moins de 1. Et cela n'est possible que lorsque le temps de descente sur l'escalator descendant n'est pas inférieur à l'intervalle entre les trains. Dans un vrai métro, où l'intervalle moyen entre les trains est de 2 minutes, toutes les gares ne peuvent pas se vanter d'une longue descente. En règle générale, même dans le métro de Saint-Pétersbourg, le temps de trajet de l'escalator est d'environ 1 minute 30 secondes, soit 0,75 fois moins que l'intervalle. De cela découle la conclusion fondamentale la plus évidente et la plus importante: si vous savez avec certitude que l'escalator de cette station se déplace moins que l'intervalle entre les trains, alors il n'est pas pratique de le parcourir.

PS Veuillez tenir compte du fait que cette tâche ne prend pas en compte la nécessité de monter dans un chariot spécifique. Il s'agit exclusivement de monter sur le quai puis de monter dans le train.

Source de données expérimentales: The Village . Merci encore!