La traduction de l'article a été préparée spécialement pour les étudiants des cours de base et avancés «Mathématiques pour la science des données».
Le théorème de Bayes est l'un des théorèmes les plus célèbres de la statistique et de la théorie des probabilités. Même si vous ne travaillez pas avec le calcul d'indicateurs quantitatifs, vous avez probablement dû vous familiariser avec ce théorème à un moment donné en préparation de l'examen.
P (A | B) = P (B | A) * P (A) / P (B)Voilà à quoi ça ressemble, mais qu'est-ce que cela signifie et comment ça marche? Aujourd'hui, nous allons découvrir et approfondir le théorème de Bayes.
Raisons de confirmer notre jugement
Quel est tout l'intérêt de la théorie des probabilités et des statistiques? L'une des utilisations les plus importantes concerne la prise de décision dans l'incertitude. Lorsque vous décidez d'effectuer une action (à moins, bien sûr, que vous soyez une personne raisonnable), vous pariez qu'après l'achèvement de cette action, cela entraînera un meilleur résultat que si cette action n'a pas eu lieu ... Mais le pari est une chose peu fiable, comment décidez-vous finalement de prendre telle ou telle mesure ou non?
D'une manière ou d'une autre, vous évaluez la probabilité de réussite, et si cette probabilité est supérieure à une certaine valeur seuil, vous faites un pas.
Ainsi, la capacité d'évaluer avec précision les chances de succès est essentielle pour prendre les bonnes décisions. Malgré le fait que le hasard jouera toujours un rôle dans le résultat final, vous devez apprendre à utiliser ces aléas correctement et à les utiliser à votre avantage au fil du temps.
C'est ici que le théorème de Bayes entre en vigueur - il nous donne une base quantitative pour maintenir notre foi dans le résultat de l'action à mesure que les facteurs environnementaux changent, ce qui, à son tour, nous permet d'améliorer le processus décisionnel au fil du temps.
Analysons la formule
Regardons à nouveau la formule:
P (A | B) = P (B | A) * P (A) / P (B)Ici:
- P (A | B) - probabilité d'occurrence de l'événement A, à condition que l'événement B se soit déjà produit;
- P (B | A) - probabilité d'occurrence de l'événement B, à condition que l'événement A se soit déjà produit. Maintenant, cela ressemble à une sorte de cercle vicieux, mais nous comprendrons bientôt pourquoi la formule fonctionne;
- P (A) - probabilité a priori (inconditionnelle) d'occurrence de l'événement A;
- P (B) - probabilité a priori (inconditionnelle) d'occurrence de l'événement B.
P (A | B) est un exemple de probabilité a posteriori (conditionnelle), c'est-à-dire une mesure de la probabilité d'un certain état du monde environnant (à savoir, l'état dans lequel l'événement B s'est produit). Alors que P (A) est un exemple de probabilité a priori, qui peut être mesurée dans n'importe quel état du monde environnant.
Regardons le théorème de Bayes en action à titre d'exemple. Supposons que vous ayez récemment suivi un cours d'analyse de données à partir de bootcamp. Vous n'avez pas reçu de réponse de la part de certaines des sociétés dans lesquelles vous avez été interrogé et commencez à vous inquiéter. Donc, vous voulez calculer la probabilité qu'une entreprise particulière vous fasse une offre d'emploi, à condition que trois jours se soient écoulés et qu'ils ne vous aient pas rappelé.
Nous réécrivons la formule en fonction de notre exemple. Dans ce cas, le résultat A (
offre ) est la réception d'une offre d'emploi et le résultat B (
NoCall ) est «aucun appel téléphonique pendant trois jours». Sur cette base, notre formule peut être réécrite comme suit:
P ( Offre | NoCall ) = P ( NoCall | Offer ) * P ( Offre ) / P ( NoCall )La valeur de
P ( Offre | NoCall ) est la probabilité de recevoir une offre, à condition qu'il n'y ait pas d'appel dans les trois jours. Cette probabilité est extrêmement difficile à évaluer.
Cependant, la probabilité inverse,
P ( NoCall | Offer ) , c'est-à-dire l'absence d'un appel téléphonique pendant trois jours, étant donné qu'au final vous avez reçu une offre d'emploi de l'entreprise, il est tout à fait possible d'attacher une certaine valeur. À partir de conversations avec des amis, des recruteurs et des consultants, vous découvrirez que cette probabilité est faible, mais parfois une entreprise peut encore garder le silence pendant trois jours si elle prévoit toujours de vous inviter à travailler. Vous évaluez donc:
P ( NoCall | Offre ) = 40%40% c'est pas mal et il semble qu'il y ait encore de l'espoir! Mais nous n'avons pas encore fini. Il nous faut maintenant évaluer
P ( Offre ) , la probabilité d'aller travailler. Tout le monde sait que trouver un emploi est un processus long et difficile, et vous devrez peut-être passer plusieurs entretiens avant de recevoir cette offre, vous évaluez donc:
P ( offre ) = 20%Il ne nous reste plus qu'à évaluer
P ( NoCall ) , la probabilité que vous ne receviez pas d'appel de l'entreprise dans les trois jours. Il y a de nombreuses raisons pour lesquelles vous ne pouvez pas être rappelé dans les trois jours - ils peuvent rejeter votre candidature ou encore mener des entretiens avec d'autres candidats, ou le recruteur est simplement malade et n'appelle donc pas. Eh bien, il existe de nombreuses raisons pour lesquelles vous pourriez ne pas avoir d'appel, vous évaluez donc cette probabilité comme:
P ( NoCall ) = 90%Et maintenant, en mettant tout cela ensemble, nous pouvons calculer
P ( Offre | NoCall ) :
P ( Offre | NoCall ) = 40% * 20% / 90% = 8,9%C'est assez petit, donc, malheureusement, il est plus rationnel de laisser de l'espoir pour cette entreprise (et de continuer à envoyer des CV à d'autres). Si cela semble encore un peu abstrait, ne vous inquiétez pas. J'ai ressenti la même chose lorsque j'ai appris pour la première fois le théorème de Bayes. Voyons maintenant comment nous en sommes arrivés à ces 8,9% (gardez à l'esprit que votre score initial de 20% était déjà bas).
L'intuition derrière la formule
Rappelez-vous, nous avons dit que le théorème bayésien fournit la base pour la confirmation de nos jugements? Alors d'où viennent-ils? Ils sont tirés de la probabilité a priori
P (A) , qui dans notre exemple est appelée
P ( offre ) , en fait, c'est notre jugement initial sur la probabilité qu'une personne reçoive une offre d'emploi. Dans notre exemple, vous pouvez supposer que la probabilité a priori est la probabilité que vous receviez une offre d'emploi au moment même où vous quittez l'entretien.
De nouvelles informations apparaissent - 3 jours se sont écoulés et l'entreprise ne vous a pas rappelé. Ainsi, nous utilisons d'autres parties de l'équation pour ajuster notre probabilité a priori d'un nouvel événement.
Regardons la probabilité
P (B | A) , qui dans notre exemple est appelée
P ( NoCall | Offer ) . Lorsque vous voyez pour la première fois le théorème de Bayes, vous vous demandez: comment savez-vous où obtenir la probabilité
P (B | A) ? Si je ne sais pas quelle est la probabilité de
P (A | B) , alors comment dois-je savoir par magie quelle est la probabilité de
P (B | A) ? Je me souviens de la phrase que
Charles Munger a dite:
"Retournez, retournez toujours!"
- Charles Munger
Il voulait dire que lorsque vous essayez de résoudre un problème difficile, vous devez le renverser et le regarder sous un angle différent. C'est exactement ce que fait le théorème de Bayes. Reformulons le théorème de Bayes en termes de statistiques afin de le rendre plus compréhensible (j'ai appris cela à
partir d'ici ):
Pour moi, par exemple, un tel record semble plus clair. Nous avons une hypothèse a priori (Hypothèse) - que nous avons obtenu un emploi, et des faits observables - des preuves (Preuve) - il n'y a pas d'appel téléphonique pendant trois jours. Maintenant, nous voulons connaître la probabilité que notre hypothèse soit correcte, en tenant compte des faits présentés. Comme décidé ci-dessus, nous avons une probabilité
P (A) = 20% .
Il est temps de tout renverser! Nous utilisons
P ( Evidence | Hypothesis ) pour examiner le problème de l'autre côté et nous demandons: «Quelle est la probabilité que ces événements se produisent dans un monde où notre hypothèse est vraie?» Donc, si nous revenons à notre exemple, nous voulons savoir dans quelle mesure il est probable que s'ils ne nous appellent pas dans les trois jours, nous serons toujours embauchés. Dans l'image ci-dessus, j'ai marqué
P ( Evidence | Hypothesis ) comme «scaler» (scaler), car ce mot reflète bien l'essence du sens. Lorsque nous la multiplions par une valeur a priori, elle diminue ou augmente la probabilité d'un événement, selon que tout événement prouvant que notre hypothèse est «nuisible». Dans notre cas, plus il y a de jours sans appel, moins nous serons appelés à travailler. 3 jours de silence, c'est déjà mauvais (ils réduisent notre probabilité a priori de 60%), tandis que 20 jours sans appel vont complètement détruire l'espoir d'obtenir un emploi. Ainsi, plus les événements de preuves s'accumulent (plus de jours passent sans appel téléphonique), plus le scaler réduit rapidement la probabilité. Un scaler est un mécanisme que le théorème de Bayes utilise pour ajuster notre jugement.
Il y a une chose avec laquelle j'ai eu du mal dans la version originale de cet article. C'était la formulation des raisons pour lesquelles
P ( Preuve | Hypothèse ) est plus facile à évaluer que P (Hypothèse | Preuve). La raison en est que
P ( Evidence | Hypothesis ) est un domaine de jugement beaucoup plus limité sur le monde. En rétrécissant la portée, nous simplifions la tâche. Nous pouvons faire une analogie avec le feu et la fumée, où le feu est notre hypothèse, et l'observation de la fumée est un événement prouvant la présence du feu.
P (feu | fumée) est plus difficile à évaluer, car beaucoup de choses peuvent provoquer de la fumée - les gaz d'échappement des voitures, les usines, la personne qui fait frire des hamburgers sur du charbon de bois. Dans le même temps,
P (fumée | feu) est plus facile à évaluer, car dans un monde où il y a du feu, il y aura presque certainement de la fumée.
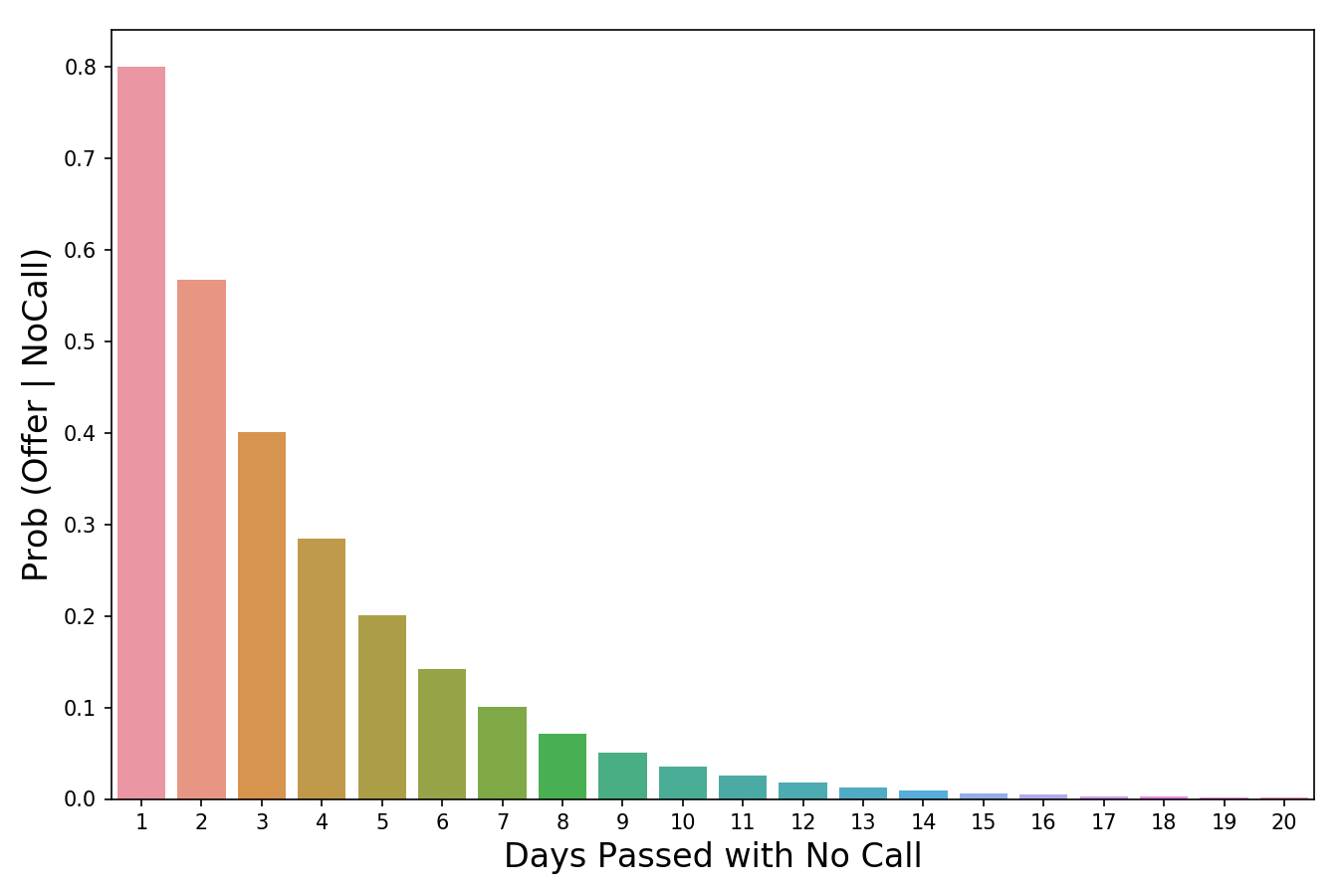La valeur de probabilité diminue à mesure que le nombre de jours s'écoule sans appel.La dernière partie de la formule,
P (B) ou
P ( Preuve ) , est le normalisateur. Comme son nom l'indique, son but est de normaliser le produit d'une probabilité a priori et d'un scaler. S'il n'y avait pas de normalisateur, nous aurions l'expression suivante:
A noter que le produit d'une probabilité a priori et d'un scaler est égal à la probabilité conjointe. Et puisque l'un des composants de
P ( Evidence ) en elle , alors la probabilité conjointe serait affectée par la faible fréquence des événements.
C'est un problème parce que la probabilité partagée est une valeur qui inclut tous les états du monde. Mais nous n'avons pas besoin de tous les États, nous avons seulement besoin des États qui ont été confirmés par des preuves d'événements. En d'autres termes, nous vivons dans un monde où les événements - des preuves ont déjà eu lieu, et leur nombre n'a plus d'importance (par conséquent, nous ne voulons pas qu'ils affectent nos calculs en principe). La division du produit d'une probabilité a priori et d'un échelonneur par
P ( preuves ) le fait passer d'une probabilité conjointe à une conditionnelle (postérieure). La probabilité conditionnelle ne prend en compte que les états du monde dans lesquels un événement à l'épreuve s'est produit, ce qui est exactement ce que nous réalisons.
Un autre point de vue à partir duquel nous pouvons voir pourquoi nous divisons le détartreur en un normalisateur est qu'ils répondent à deux questions importantes - et leur attitude combine ces informations. Prenons un exemple de mon récent
article Bayes . Supposons que nous essayons de savoir si l'animal observé est un chat, sur la base d'un seul signe - la dextérité. Tout ce que nous savons, c'est que l'animal dont nous parlons est agile.
- Le détartreur nous dit quel pourcentage de chats sont bons avec la dextérité. Cette valeur devrait être assez élevée, disons 0,90.
- Le normalisateur nous indique en principe quel pourcentage de pièges à animaux. Cette valeur doit être moyenne, disons 0,50.
- Le rapport 0,90 / 0,50 = 1,8 indique que vous devez changer la probabilité a priori, car si vous pensiez précédemment le contraire, il est temps de changer d'avis, car vous avez très probablement affaire à un chat. La raison pour laquelle cela peut être pensé est que nous avons observé des preuves que l'animal est agile. Ensuite, nous avons constaté que la proportion de chats adroits est supérieure à la proportion d'animaux adroits en général. Considérant que pour le moment nous ne connaissons qu'un tel élément de preuve et rien de plus, il serait raisonnable de reconsidérer nos croyances dans le sens des pensées que nous regardons toujours un chat.
Pour résumer
Maintenant que nous savons comment interpréter chaque partie de la formule, nous pouvons enfin tout assembler et regarder ce qui s'est passé:
- Immédiatement après l'entretien, nous établissons une probabilité a priori - la probabilité d'être embauché est de 20%.
- Plus il y a de jours sans appel, moins il est probable que nous serons embauchés. Par exemple, après trois jours sans appel, nous pensons que dans un monde où nous pouvons obtenir ce poste, il n'y a que 40% de chances que l'entreprise tire si longtemps avant de vous appeler. Multipliez le détartreur par une probabilité a priori et obtenez 20% * 40% = 8%
- Enfin, nous comprenons que 8% a été calculé pour toutes les conditions dans lesquelles le monde peut être. Mais nous ne sommes préoccupés que par les conditions dans lesquelles nous n'avons pas été appelés depuis trois jours. Afin de ne travailler qu'avec ces conditions, nous prenons pour 90% la probabilité a priori qu'il n'y aura pas d'appel dans les trois jours et nous obtenons un normalisateur. Nous divisons le 8% précédemment reçu par le normalisateur 8% / 90% = 8,9% et obtenons la réponse finale. Au total, dans toutes les conditions du monde, si vous n'avez pas reçu d'appel de l'entreprise dans les trois jours, la probabilité de décrocher un emploi n'est que de 8,9%.
J'espère que cet article vous a été utile!