Splines dans les graphismes 3D, l'option la plus automatisée

Il y a environ un mois, j'ai commencé à apprendre Python à partir du livre de Dawson et je me suis réveillé profondément en train d'écrire mon jeu sous pygame. Les savoirs traditionnels étaient tels qu'il semblait plus prometteur de faire un jeu avec des graphiques pseudo-tridimensionnels en remplissant les surfaces enregistrées des splines 3D en sprites. Je vais écrire sur ce dernier.

Donc, il y a des polygones (il est plus facile de travailler avec des quadrangles) sur lesquels nous voulons étirer les surfaces cubiques afin qu'elles s'emboîtent assez facilement - ces surfaces sont des splines.



Il est plus pratique de présenter une spline pour un polygone en fonction

$$

$$g (u, v) = v \ cdot g_1 (u) + (1 - v) \ cdot g_2 (u) + u \ cdot g_3 (v) + (1-u) \ cdot g_4 (v) (1)$$

Ici

$$

$$g_1, g_2, g_3, g_4$$

- polynômes cubiques satisfaisant certaines conditions aux limites (dans la figure ci-dessous - courbes vert clair et rouge, et conditions initiales dérivées - vecteurs lilas et bleus); u et v varient de 0 à 1.



Dans cette interprétation, certains degrés sont perdus (produits de 2 et 3 degrés de paramètres), mais les coefficients polynomiaux peuvent être trouvés en ne spécifiant que 12 vecteurs de conditions initiales (4 polygones et vecteurs dérivés par rapport à u et v pour chaque point). Aux jonctions, les splines coïncident si des conditions initiales similaires sont définies pour les polygones voisins (les vecteurs dérivés doivent être colinéaires, la surface passe par les mêmes points du polygone).

Un problème - le dérivé avec une telle déclaration du problème sur toute la frontière peut ne pas coïncider - il y aura de petits artefacts aux jonctions. Vous pouvez imaginer 4 autres conditions pour corriger cela et ajouter soigneusement un autre terme à la formule

$$

$$u \ cdot v \ cdot (u-1) \ cdot (v-1) \ cdot g_5 (u, v)$$

ce qui ne gâche pas les frontières, mais c'est un sujet pour un article séparé.

Une alternative est la surface de Bézier , mais elle propose de définir 16 paramètres de signification mathématique incompréhensible (pour moi), c'est-à-dire on suppose que l'artiste travaillera de ses propres mains. Ce n'est pas très approprié pour moi, donc un vélo avec des béquilles suit.

Les coefficients (1) sont plus facilement calculés en trouvant la matrice inverse à la matrice des valeurs et des dérivées dans les coins et en multipliant par les conditions d'entrée (trois fois, pour chaque coordonnée). La matrice peut être la suivante:


NumPy en fait un excellent travail.

Une question demeure - où trouver les vecteurs de dérivés. On suppose qu'ils doivent en quelque sorte être sélectionnés en fonction de la position des points voisins (pour le polygone) et pour des raisons de lissage.
Pour moi personnellement, il était encore complètement contre-intuitif de gérer la longueur du vecteur dérivé. La direction est compréhensible, mais la longueur?

En conséquence, l'algorithme suivant est né:

1. À la première étape, une classification des points a lieu. Dans le graphique (quels points des polygones et leurs connexions spécifient), les cycles de longueur 4 sont recherchés et stockés, et en outre, les voisins qui conviennent le mieux au rôle d'extension des bords du polygone sont enregistrés (il est déterminé à l'avance quels bords correspondent à un changement du paramètre u et qui correspondent à v). Voici un morceau de code qui recherche, trie et mémorise les voisins pour le 0ème point d'un cycle:


De plus, lors de la construction de la spline, la dérivée le long du bord (par exemple, par rapport au paramètre u) au point du polygone est sélectionnée en fonction de l'emplacement de deux points du bord et d'un point adjacent (que ce soit les points vec1, vec2 et vec3; le point auquel la dérivée est recherchée est le deuxième).



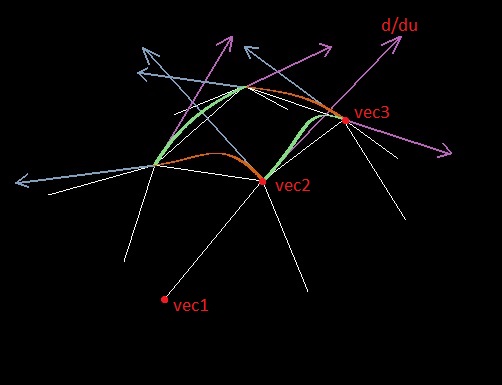
Au début, j'ai essayé d'utiliser le vecteur normalisé vec3 - vec1 (comme j'ai appliqué le théorème de Lagrange) pour ce rôle, mais des problèmes sont survenus précisément avec la longueur du vecteur dérivé - en faire une constante était une mauvaise idée.

Digression lyrique:

Pour une petite illustration de ce qu'est le vecteur dérivé dans la version paramétrique, nous nous tournons vers une analogie bidimensionnelle simple - voici un morceau d'arc de cercle:

$$

$$g (u) = (Rsin (u \ pi / 2), Rcos (u \ pi / 2))$$

$$

$$g '(u) = (R \ pi / 2 \ cdot cos (u \ pi / 2), -R \ pi / 2 \ cdot sin (u \ pi / 2))$$

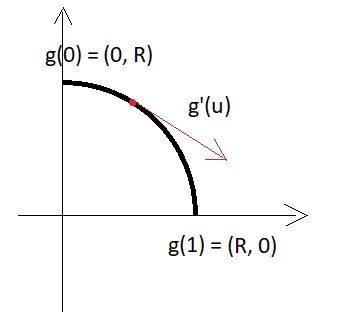
C'est-à-dire module dérivé = R * pi / 2 et, d'une manière générale, dépend de la taille du morceau de l'arc, que nous définissons par le paramètre.

Que faire maintenant? Leo Nikolaevich Tolstoy nous a légué que tout est rond = bon, donc, si nous réglons la dérivée à un point comme si nous voulions y construire un arc, nous obtiendrons une belle courbe lisse.

La fin de la digression.

La deuxième étape de la recherche dérivée:

2. A travers nos trois points vec1, vec2, vec3 nous construisons un plan, dans ce plan nous recherchons un cercle qui passe par les trois points. La dérivée souhaitée sera dirigée le long de la tangente au cercle au point vec2, et le module du vecteur de la dérivée doit être égal au produit du rayon du cercle et de l'angle du secteur, qui forment deux points de la face du polygone (semblable à notre simple analogie plate de la digression lyrique).

$$

$$g '= R \ cdot \ phi$$

Tout semble simple, voici le code de fonction par exemple (NumPy est à nouveau utilisé):


Eh bien, en général, tout cela fonctionne d'une manière ou d'une autre. Pour démonstration, j'ai pris un cube 5x5x5 et changé la position des points avec un randomiseur: