Introduction aux dépendances fonctionnelles

Dans cet article, nous parlerons des dépendances fonctionnelles dans les bases de données - ce qu'elles sont, où elles sont appliquées et quels algorithmes existent pour leur recherche.

Nous considérerons les dépendances fonctionnelles dans le contexte des bases de données relationnelles. Parlant très grossièrement, dans de telles bases de données, les informations sont stockées sous forme de tableaux. De plus, nous utilisons des concepts approximatifs, qui dans une théorie relationnelle stricte ne sont pas interchangeables: nous appellerons la table elle-même une relation, des colonnes - attributs (leur ensemble - un diagramme de relation), et un ensemble de valeurs de ligne sur un sous-ensemble d'attributs - un tuple.



Par exemple, dans le tableau ci-dessus, (Benson, M, M organe ) est un tuple d'attributs (Patient, Sexe, Médecin) .
Plus formellement, ceci est écrit comme suit: $$$t_ {1}$[ Patient, Paul, docteur ] = (Benson, M, M organe) .
Nous pouvons maintenant introduire le concept de dépendance fonctionnelle (FZ):

Définition 1. La relation R satisfait la loi fédérale X → Y (où X, Y ⊆ R) si et seulement si pour des tuples $$$t_ {1}$, $$$t_ {2}$∈ R détient: si $$$t_ {1}$[X] = $$$t_ {2}$[X] puis $$$t_ {1}$[Y] = $$$t_ {2}$[Y]. Dans ce cas, on dit que X (un déterminant ou un ensemble d'attributs définissant) définit fonctionnellement Y (un ensemble dépendant).

En d'autres termes, la présence de la loi fédérale X → Y signifie que si nous avons deux tuples dans R et qu'ils coïncident dans les attributs de X , ils coïncideront également dans les attributs de Y.
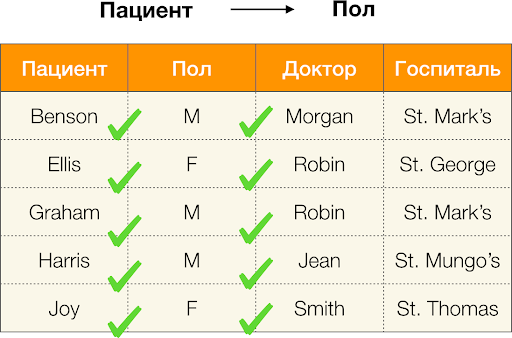
Et maintenant en ordre. Considérez les attributs Patient et Sexe pour lesquels nous voulons savoir s'il existe ou non des dépendances entre eux. Pour tant d'attributs, les dépendances suivantes peuvent exister:

1. Patient → Sexe
2. Sexe → Patient

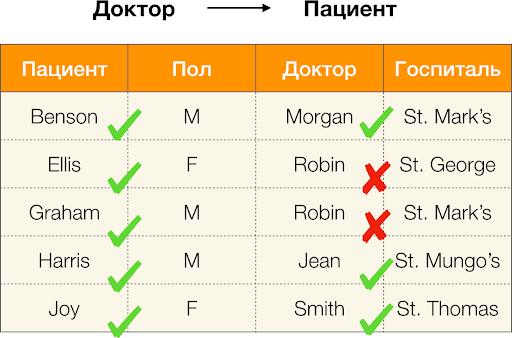
Selon la définition ci-dessus, afin de conserver la première dépendance, une seule valeur de la colonne Sexe doit correspondre à chaque valeur unique de la colonne Patient . Et pour l'exemple de table, cela est vrai. Cependant, cela ne fonctionne pas dans la direction opposée, c'est-à-dire que la deuxième dépendance n'est pas remplie et l'attribut Paul n'est pas un déterminant pour le patient . De même, si vous prenez la dépendance Médecin → Patient , vous pouvez voir qu'elle est violée, car la valeur Robin pour cet attribut a plusieurs valeurs différentes - Ellis et Graham .

Ainsi, les dépendances fonctionnelles permettent de déterminer les relations existantes entre les ensembles d'attributs de table. Désormais, nous considérerons les relations les plus intéressantes, ou plutôt X → Y telles qu'elles sont:

• non triviale, c'est-à-dire que le côté droit de la dépendance n'est pas un sous-ensemble de la gauche (Y ̸⊆ X) ;
• minimale, c'est-à-dire qu'il n'y a pas une telle dépendance Z → Y telle que Z ⊂ X.

Les dépendances considérées jusqu'à présent étaient strictes, c'est-à-dire qu'elles n'incluaient aucune violation sur la table, mais à côté d'eux il y a aussi celles qui permettent une certaine incohérence entre les valeurs des tuples. Ces dépendances sont placées dans une classe distincte, appelée approximative, et autorisées à être violées sur un certain nombre de tuples. Ce montant est régulé par l'indicateur d'erreur emax maximum. Par exemple, la proportion d'erreur $$$e_ {max}$= 0,01 peut signifier que la dépendance peut être violée par 1% des tuples disponibles sur l'ensemble d'attributs considéré. Autrement dit, pour 1000 enregistrements, un maximum de 10 tuples peut violer la loi fédérale. Nous considérerons une métrique légèrement différente basée sur des valeurs différentes par paire des tuples comparés. Pour la dépendance X → Y de la relation r, elle est considérée comme suit:

$$

$$e (X \ rightarrow Y, r) = \ frac {| \ {(t_1, t_2) \ in r ^ 2 \ | \ t_1 [X] = t_2 [X] \ wedge t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ 2 | - | r |}$$

Nous calculons l'erreur pour Médecin → Patient à partir de l'exemple ci-dessus. Nous avons deux tuples, dont les valeurs diffèrent sur l'attribut Patient , mais coïncident sur le docteur : $$$t_ {1}$[ Docteur, patient ] = ( Robin, Ellis ) et $$$t_ {2}$[ Docteur, patient ] = ( Robin, Graham ). Suite à la définition de l'erreur, nous devons prendre en compte toutes les paires en conflit, ce qui signifie qu'il y en aura deux: ( $$$t_ {1}$, $$$t_ {2}$) et son inversion ( $$$t_ {2}$, $$$t_ {1}$) Remplacez dans la formule et obtenez:

$$

$$\ frac {2} {5 ^ 2 - 5} = 0,1$$

Essayons maintenant de répondre à la question: «Pourquoi est-ce tout?». En fait, les lois fédérales sont différentes. Le premier type est les dépendances qui sont déterminées par l'administrateur au stade de la conception de la base de données. Habituellement, ils sont peu nombreux, ils sont stricts et l'application principale est la normalisation des données et la conception du schéma de relation.

Le deuxième type est celui des dépendances représentant des données «cachées» et des relations auparavant inconnues entre les attributs. Autrement dit, de telles dépendances n'étaient pas envisagées au moment de la conception et se trouvent déjà pour l'ensemble de données existant, de sorte que, sur la base de l'ensemble des lois fédérales identifiées, pour tirer des conclusions sur les informations stockées. C'est avec de telles dépendances que nous travaillons. Ils sont engagés dans tout un domaine de l'extraction de données avec diverses techniques de recherche et algorithmes construits sur leur base. Voyons comment les dépendances fonctionnelles trouvées (exactes ou approximatives) dans toutes les données peuvent être utiles.



Aujourd'hui, le nettoyage des données fait partie des principaux domaines d'utilisation des dépendances. Elle implique le développement de processus d'identification des «données sales» avec leur correction ultérieure. Les représentants brillants des «données sales» sont les doublons, les erreurs de données ou les fautes de frappe, les valeurs manquantes, les données obsolètes, les espaces supplémentaires et similaires.

Exemple d'erreur de données:



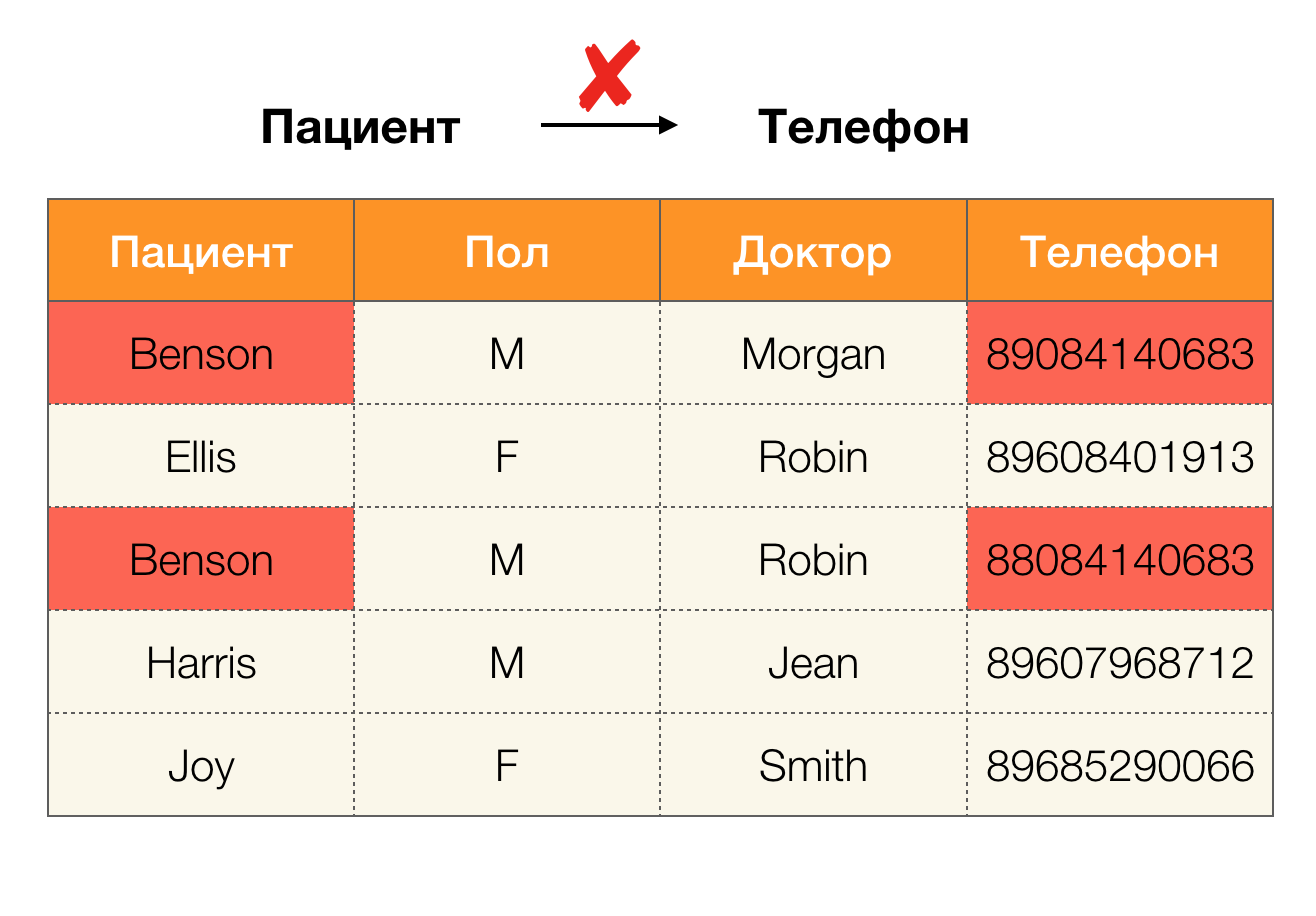
Exemples de doublons dans les données:



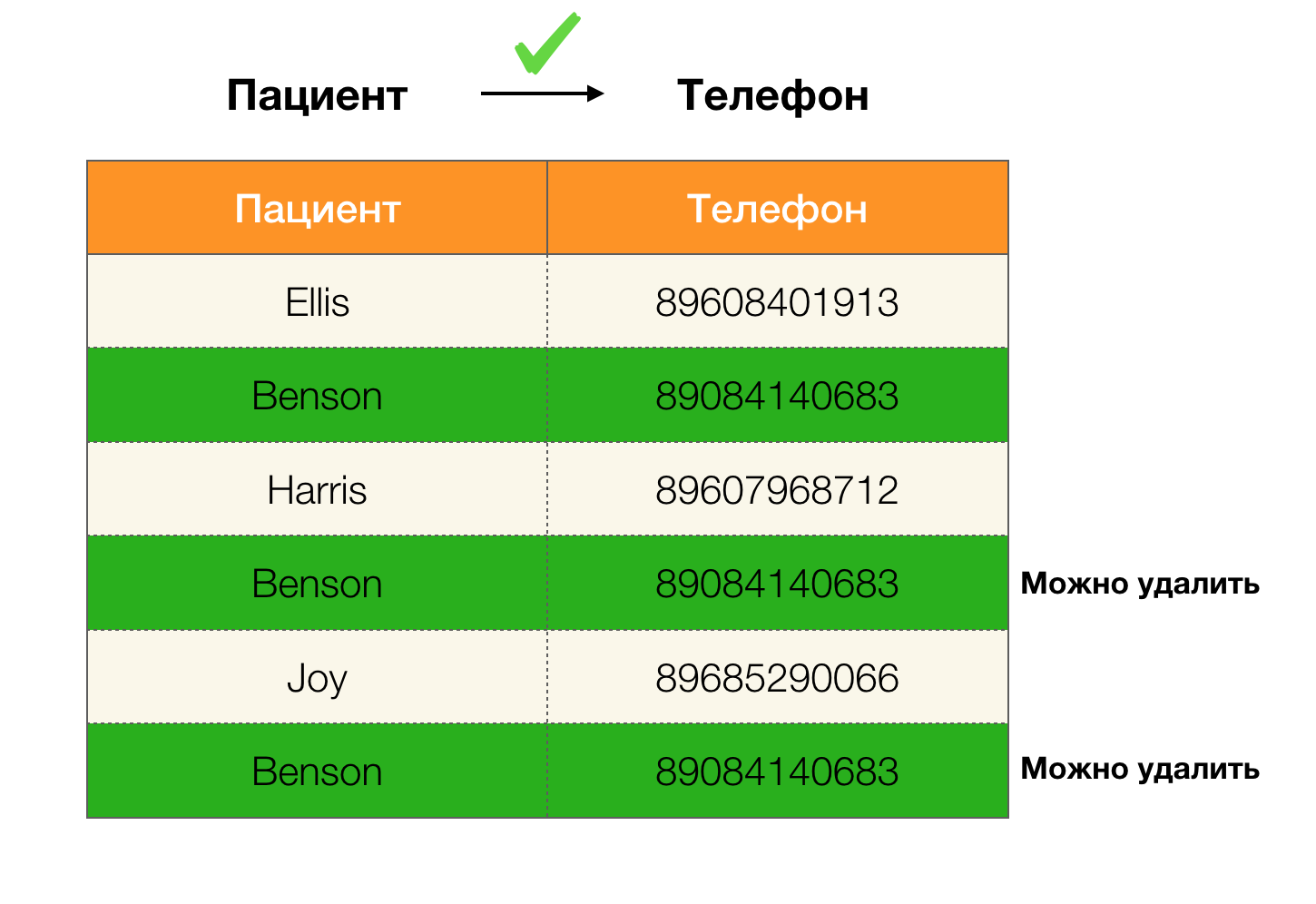
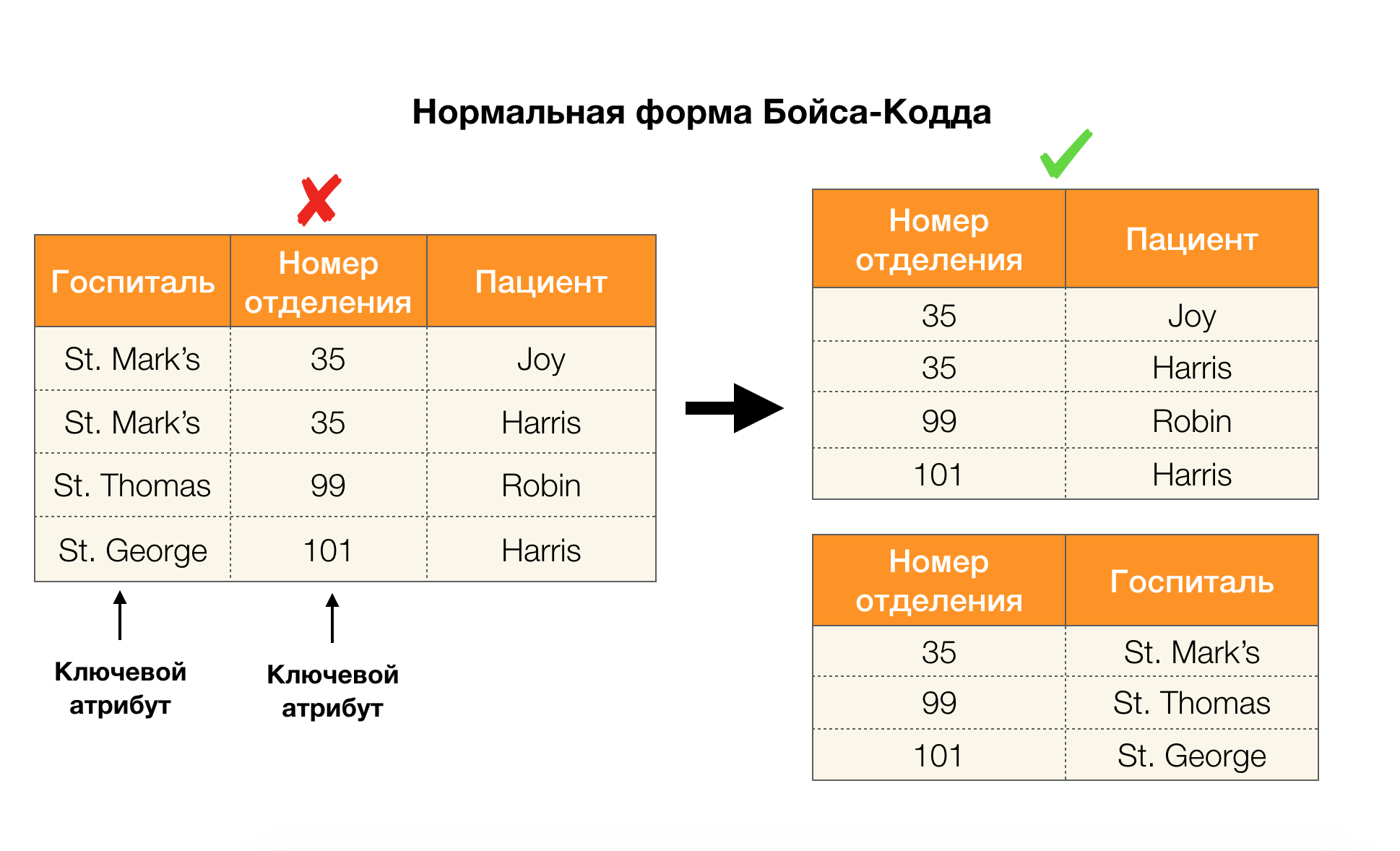
Par exemple, nous avons un tableau et un ensemble de lois fédérales qui doivent être exécutées. Dans ce cas, le nettoyage des données implique de modifier les données afin que les lois fédérales soient correctes. Dans le même temps, le nombre de modifications devrait être minime (pour cette procédure, il existe des algorithmes sur lesquels nous ne nous concentrerons pas dans cet article). Voici un exemple d'une telle conversion de données. À gauche se trouve la relation initiale, dans laquelle, évidemment, les lois fédérales nécessaires ne sont pas remplies (un exemple de violation de l'une des lois fédérales est surligné en rouge). À droite, une relation mise à jour dans laquelle les cellules vertes affichent des valeurs modifiées. Après une telle procédure, les dépendances nécessaires ont commencé à se maintenir.



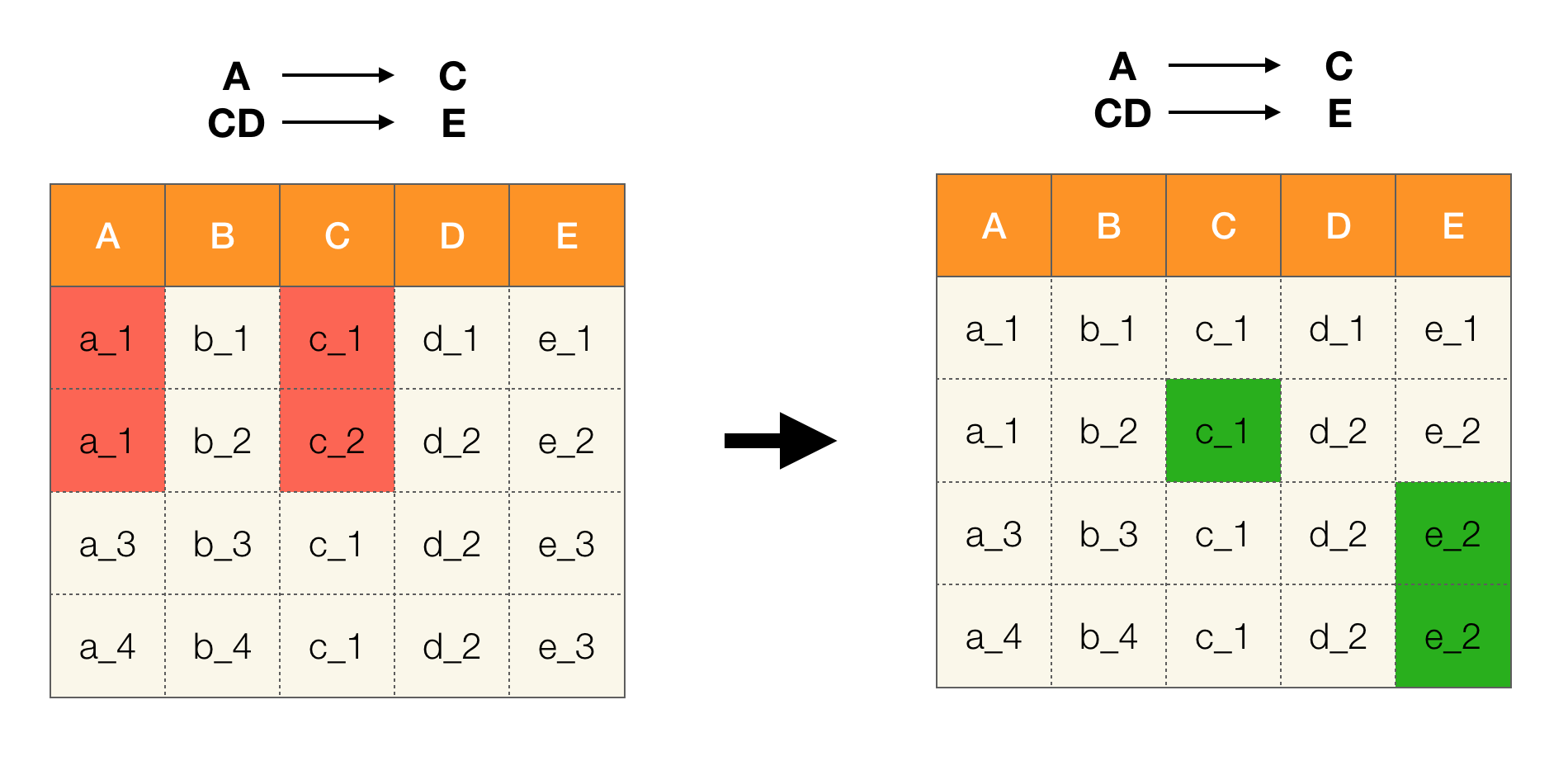
Une autre application populaire est la conception de bases de données. Ici, il convient de rappeler les formes normales et la normalisation. La normalisation est le processus d'alignement d'une relation avec un certain ensemble d'exigences, chacune étant déterminée à sa manière par une forme normale. Nous n'écrirons pas les exigences des différentes formes normales (cela se fait dans n'importe quel livre sur le cours DB pour les débutants), mais nous notons seulement que chacun d'eux utilise le concept de dépendances fonctionnelles à sa manière. En effet, les lois fédérales sont intrinsèquement des contraintes d'intégrité qui sont prises en compte lors de la conception d'une base de données (dans le cadre de cette tâche, les lois fédérales sont parfois appelées super-clés).

Considérez leur application pour les quatre formes normales dans l'image ci-dessous. Rappelons que la forme Boyce-Codd normale est plus stricte que la troisième forme, mais moins stricte que la quatrième. Nous ne considérons pas encore ce dernier, car sa formulation nécessite une compréhension des dépendances à valeurs multiples, qui ne nous intéressent pas dans cet article.






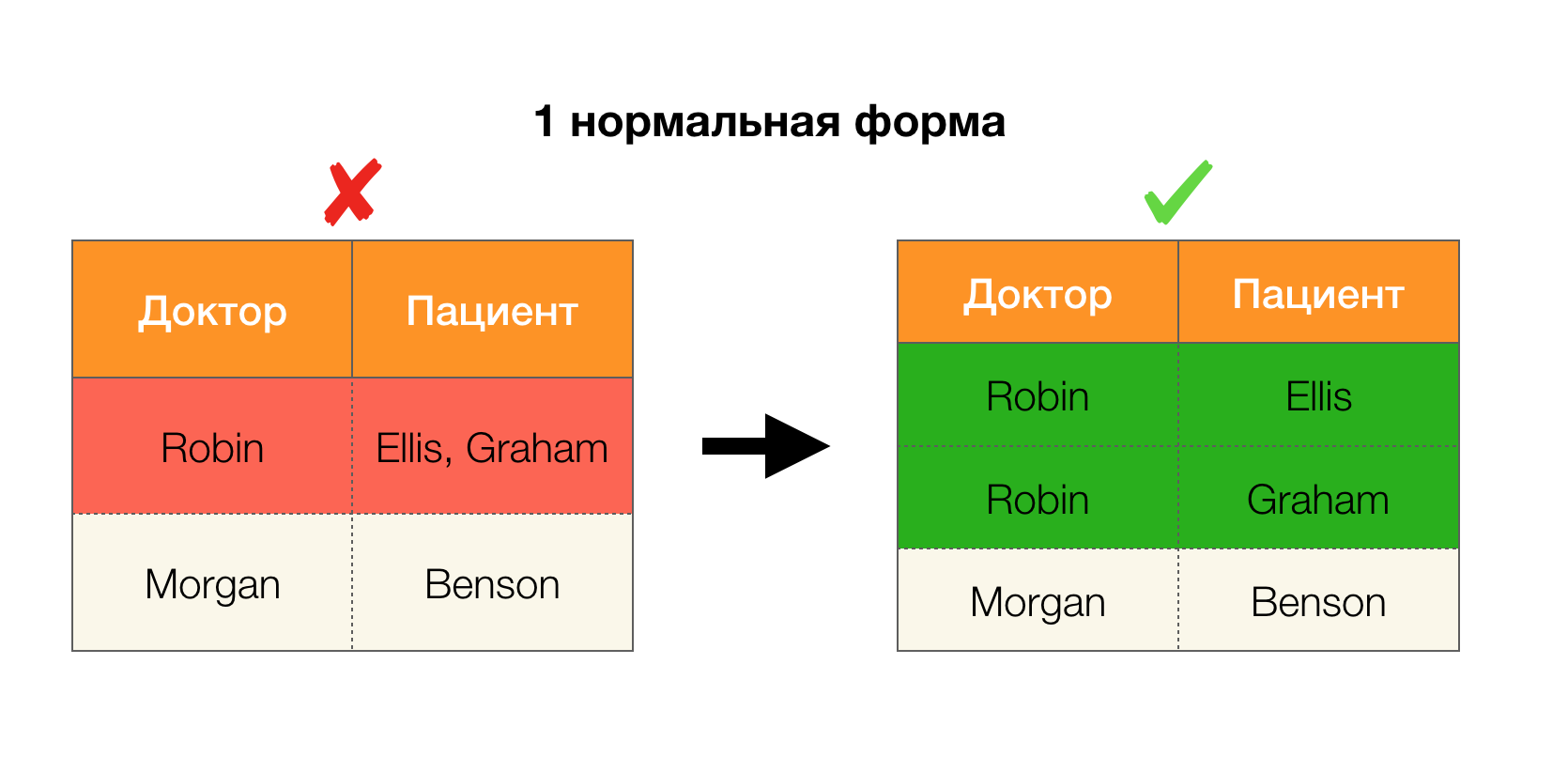
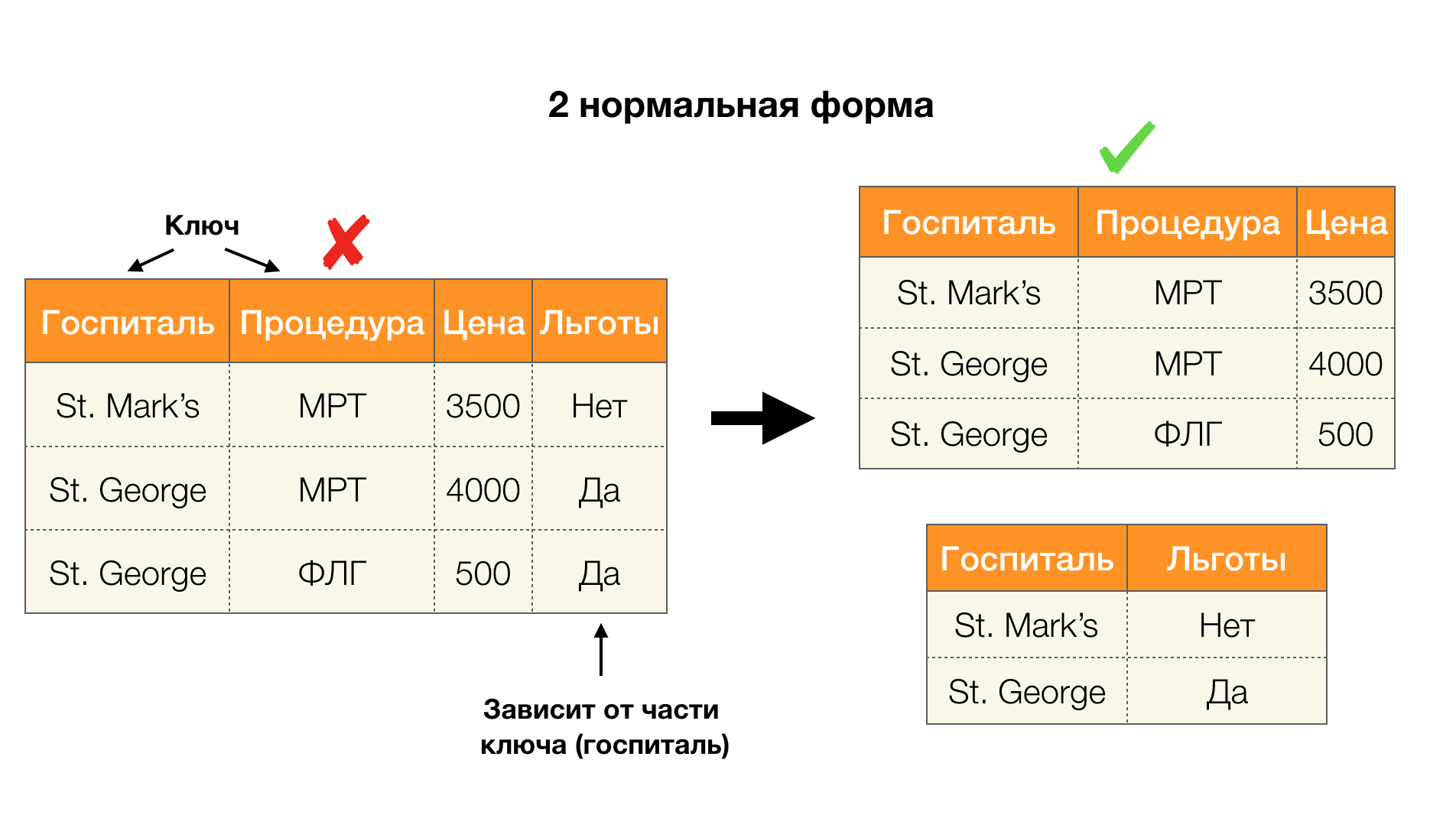
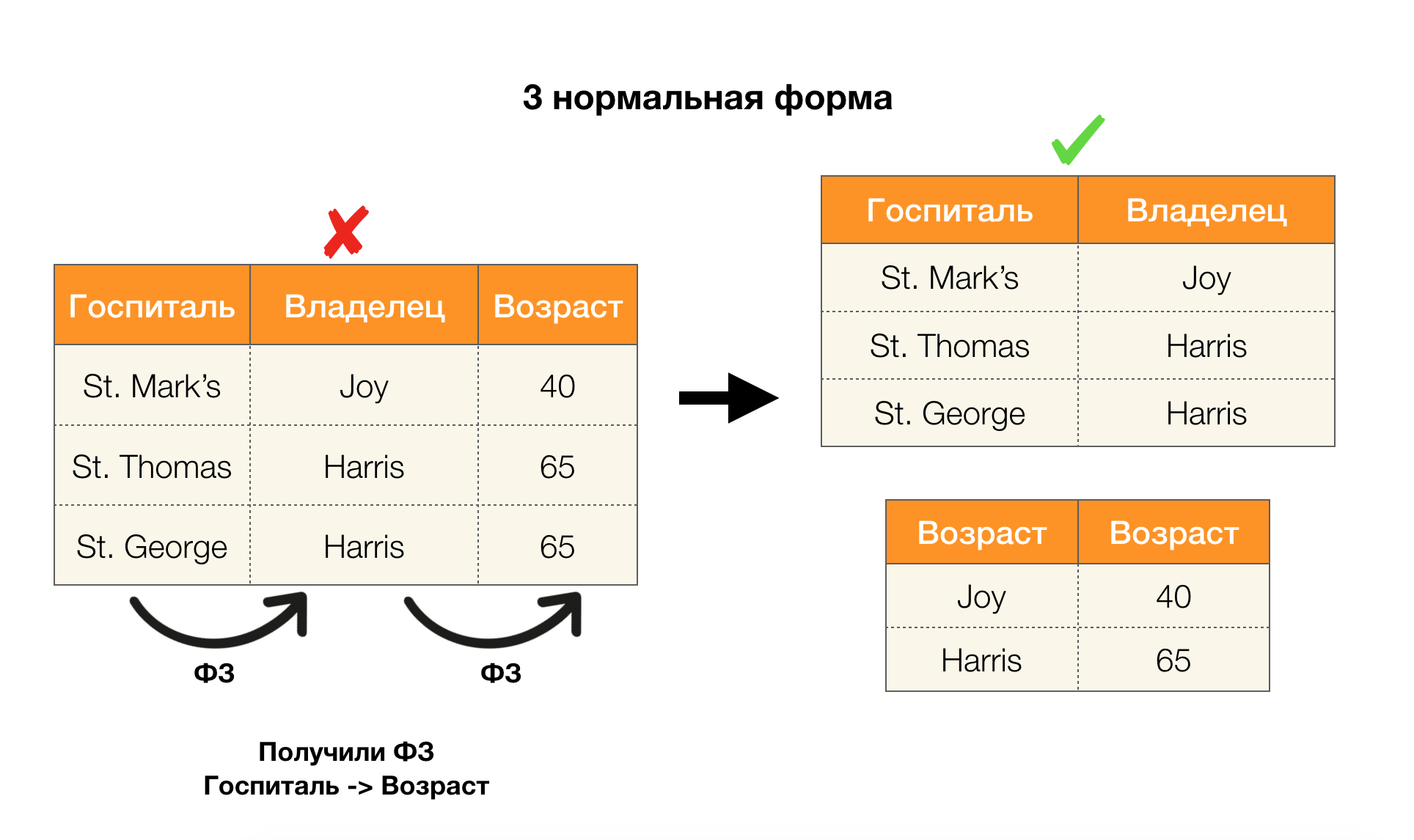
Un autre domaine dans lequel les dépendances ont trouvé leur application est la réduction de la dimension de l'espace des caractéristiques dans des tâches telles que la construction d'un classifieur bayésien naïf, l'identification des caractéristiques significatives et la reparamétrisation du modèle de régression. Dans les articles originaux, ce problème est appelé la détermination des fonctionnalités redondantes et la pertinence des fonctionnalités [5, 6], et il est résolu avec l'utilisation active des concepts de base de données. Avec l'avènement de tels travaux, nous pouvons dire qu'il existe aujourd'hui une demande de solutions qui permettent de combiner la base de données, l'analyse et la mise en œuvre des problèmes d'optimisation ci-dessus en un seul outil [7, 8, 9].

Il existe de nombreux algorithmes (à la fois modernes et pas très) pour rechercher la loi fédérale dans un ensemble de données. Ces algorithmes peuvent être divisés en trois groupes:

• Algorithmes utilisant la traversée de réseaux algébriques (algorithmes de traversée de réseau)
• Algorithmes basés sur la recherche de valeurs cohérentes (algorithmes de di ff érence et d'accord)
• Algorithmes de comparaison par paire (algorithmes d'induction de dépendance)
  

Une brève description de chaque type d'algorithme est présentée dans le tableau ci-dessous:


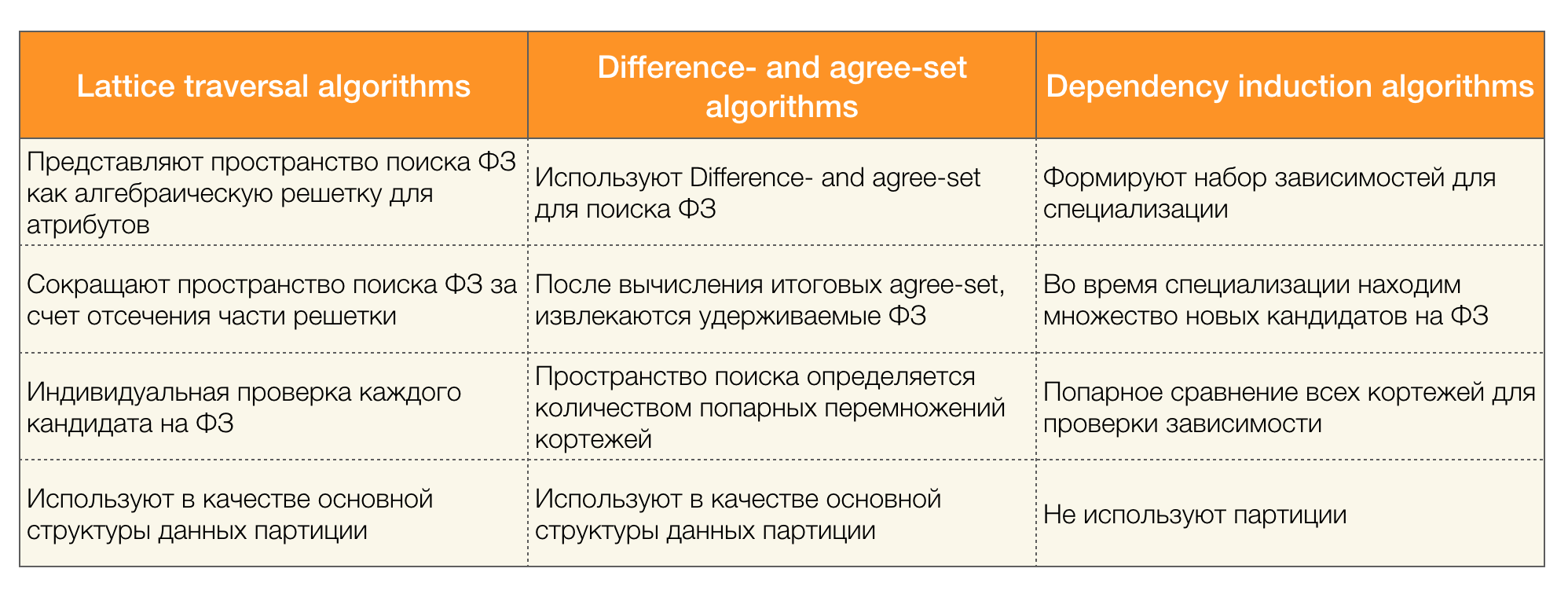
Plus de détails sur cette classification peuvent être lus [4]. Voici des exemples d'algorithmes pour chaque type:





Actuellement, de nouveaux algorithmes apparaissent qui combinent plusieurs approches de la recherche de dépendances fonctionnelles à la fois. Des exemples de tels algorithmes sont Pyro [2] et HyFD [3]. Une analyse de leur travail est attendue dans les articles suivants de cette série. Dans cet article, nous analyserons uniquement les concepts de base et le lemme qui sont nécessaires pour comprendre les techniques de détection des dépendances.

Commençons par un simple - di ff érence- et accord-ensemble, utilisé dans le deuxième type d'algorithmes. Di ff erence-set est un ensemble de tuples qui ne correspondent pas en valeurs, et d'accord-set, au contraire, sont des tuples qui correspondent en valeur. Il convient de noter que dans ce cas, nous ne considérons que le côté gauche de la dépendance.

Un réseau important qui a été rencontré ci-dessus est également le réseau algébrique. Étant donné que de nombreux algorithmes modernes fonctionnent sur ce concept, nous devons avoir une idée de ce que c'est.

Pour introduire le concept de réseau, il est nécessaire de définir un ensemble partiellement ordonné (ou un ensemble partiellement ordonné, pour un poset court).

Définition 2. On dit que l'ensemble S est partiellement ordonné par la relation binaire ⩽ si pour tout a, b, c ∈ S les propriétés suivantes sont satisfaites:

1. Réflexivité, c'est-à-dire a ⩽ a
2. Antisymétrie, c'est-à-dire que si a ⩽ b et b ⩽ a, alors a = b
3. Transitivité, c'est-à-dire que pour a ⩽ b et b ⩽ c, il s'ensuit que a ⩽ c
   

Une telle relation est appelée une relation d'ordre partiel (non strict), et l'ensemble lui-même est appelé un ensemble partiellement ordonné. Notation formelle: ⟨S, ⩽⟩.

Comme exemple le plus simple d'un ensemble partiellement ordonné, nous pouvons prendre l'ensemble de tous les nombres naturels N avec la relation habituelle d'ordre ⩽. Il est facile de vérifier que tous les axiomes nécessaires sont satisfaits.

Exemple plus significatif. Considérons l'ensemble de tous les sous-ensembles {1, 2, 3} ordonné par la relation d'inclusion ⊆. En effet, cette relation satisfait toutes les conditions d'ordre partiel, donc ⟨P ({1, 2, 3}), ⊆⟩ est un ensemble partiellement ordonné. La figure ci-dessous montre la structure de cet ensemble: si d'un élément vous pouvez marcher le long des flèches vers un autre élément, alors elles sont en relation avec l'ordre.



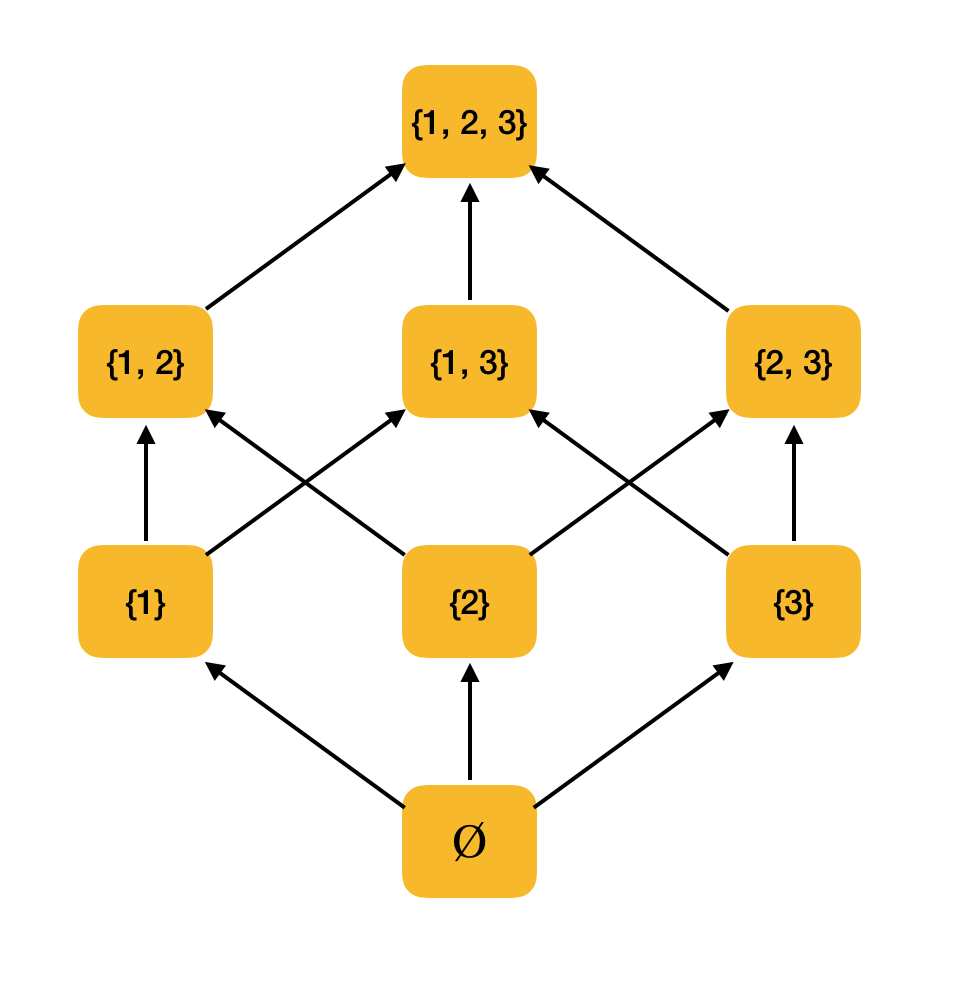
Nous aurons besoin de deux définitions plus simples du domaine des mathématiques - supremum et infimum.

Définition 3. Soit ⟨S, ⩽⟩ un ensemble partiellement ordonné, A ⊆ S. La limite supérieure de A est un élément u ∈ S tel que ∀x ∈ A: x ⩽ u. Soit U l'ensemble de toutes les bornes supérieures de A. Si U a le plus petit élément, alors il est appelé supremum et est noté sup A.

De même, le concept d'une limite inférieure exacte est introduit.

Définition 4. Soit ⟨S, ⩽⟩ un ensemble partiellement ordonné, A ⊆ S. La limite inférieure de A est un élément l ∈ S tel que ∀x ∈ A: l ⩽ x. Soit L l'ensemble de toutes les bornes inférieures de A. Si L a le plus grand élément, alors il est appelé infimum et est noté inf A.

Considérons, par exemple, l'ensemble partiellement ordonné ci-dessus ⟨P ({1, 2, 3}), et y trouvons le supremum et l'infimum:



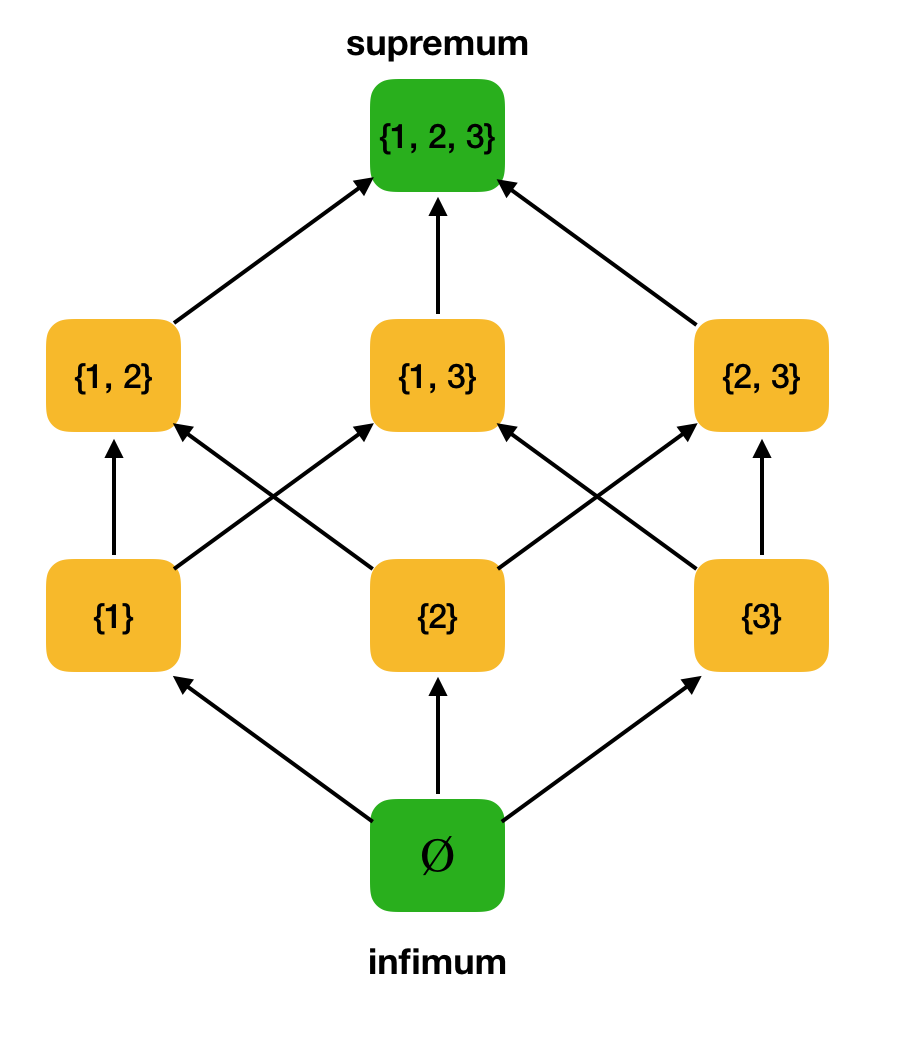
Nous pouvons maintenant formuler la définition d'un réseau algébrique.

Définition 5. Soit ⟨P, ⩽⟩ un ensemble partiellement ordonné tel que chaque sous-ensemble à deux éléments ait des bornes supérieure et inférieure exactes. Alors P est appelé un réseau algébrique. De plus, sup {x, y} s'écrit comme x ∨ y, et inf {x, y} - comme x ∧ y.

Nous vérifions que notre exemple de travail ⟨P ({1, 2, 3}), ⊆⟩ est un réseau. En effet, pour tout a, b ∈ P ({1, 2, 3}), a∨b = a∪b, et a∧b = a∩b. Par exemple, considérez les ensembles {1, 2} et {1, 3} et trouvez leur infimum et leur supremum. Si nous les croisons, nous obtenons l'ensemble {1}, qui sera l'infimum. Nous obtenons le supremum par leur union - {1, 2, 3}.

Dans les algorithmes de détection FD, l'espace de recherche est souvent représenté sous la forme d'un réseau, où les ensembles d'un élément (lire le premier niveau du réseau de recherche, où la partie gauche des dépendances se compose d'un attribut) sont chaque attribut de la relation d'origine.
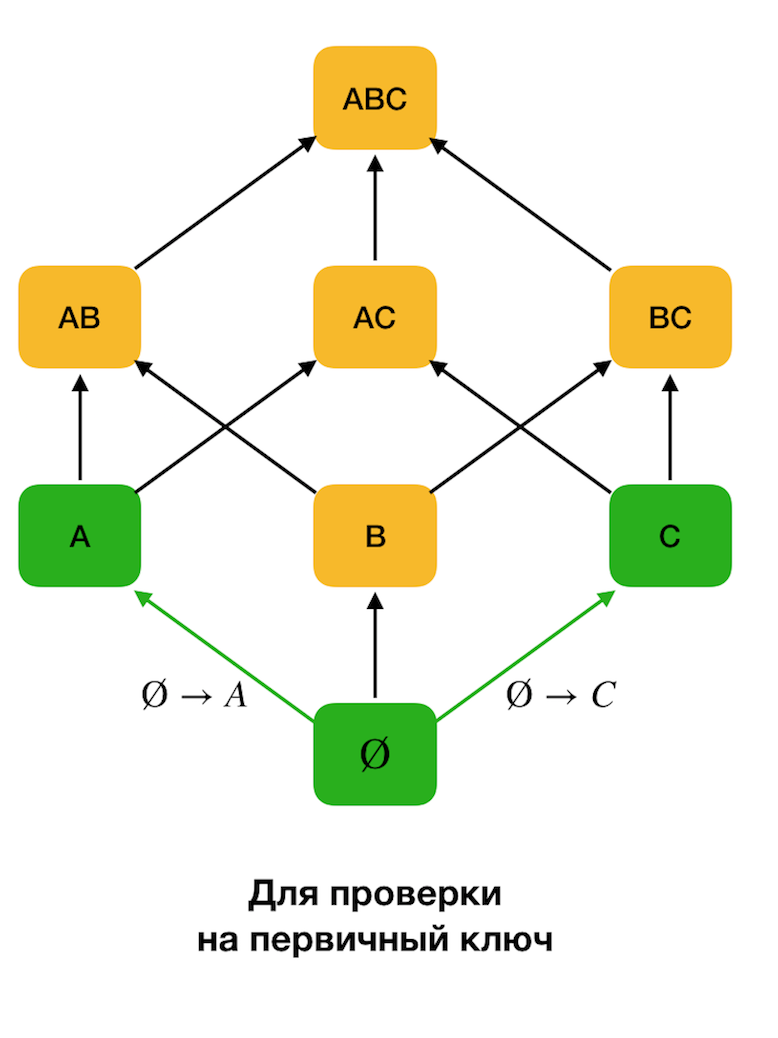
Au début, les dépendances de la forme ∅ → Attribut unique sont considérées. Cette étape vous permet de déterminer quels attributs sont des clés primaires (il n'y a pas de déterminants pour de tels attributs, et donc le côté gauche est vide). De plus, ces algorithmes remontent le réseau. Il convient de noter que le réseau ne peut pas être contourné tous, c'est-à-dire que si la taille maximale souhaitée de la partie gauche est transmise à l'entrée, l'algorithme ne dépassera pas le niveau avec cette taille.

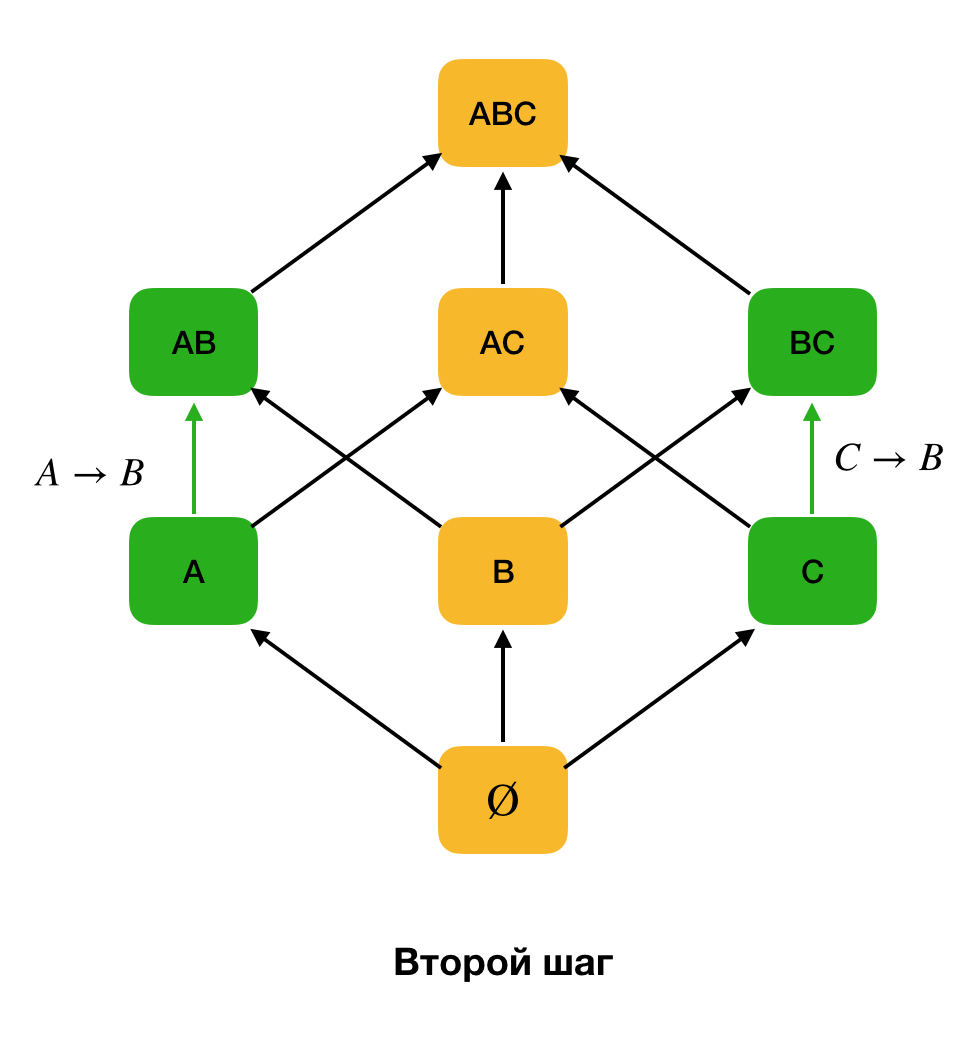
La figure ci-dessous montre comment vous pouvez utiliser le réseau algébrique dans le problème de recherche de la loi fédérale. Ici, chaque arête ( X, XY ) représente une dépendance X → Y. Par exemple, nous sommes passés par le premier niveau et nous savons que la dépendance A → B est conservée (nous l'afficherons par la connexion verte entre les sommets A et B ). Par conséquent, lorsque nous remontons le réseau vers le haut, nous ne pouvons pas vérifier la dépendance A, C → B , car elle ne sera plus minimale. De même, nous ne le testerions pas si la dépendance C → B était conservée.




De plus, en règle générale, tous les algorithmes de recherche FZ modernes utilisent une telle structure de données comme une partition (partition supprimée [1] dans la source d'origine). La définition formelle de la partition est la suivante:

Définition 6. Soit X ⊆ R l'ensemble des attributs de la relation r. Un cluster est un ensemble d'indices de tuples de r qui ont la même valeur pour X, c'est-à-dire c (t) = {i | ti [X] = t [X]}. La partition est un ensemble de clusters, à l'exclusion des clusters de longueur unitaire:

$$

$$\ pi (X): = \ {c (t) | t \ in r \ coin | c (t) | > 1 \}$$

En termes simples, la partition de l'attribut X est un ensemble de listes, où chaque liste contient des numéros de ligne avec les mêmes valeurs pour X. Dans la littérature moderne, une structure représentant des partitions est appelée un index de liste de positions (PLI). Les clusters de longueur d'unité sont exclus pour la compression PLI car ce sont des clusters contenant uniquement un numéro d'enregistrement avec une valeur unique qui sera toujours facile à définir.

Prenons un exemple. Revenons à la même table avec les patients et construisons des partitions pour les colonnes Patient et Paul (une nouvelle colonne est apparue à gauche, dans laquelle les numéros de ligne de la table sont marqués):





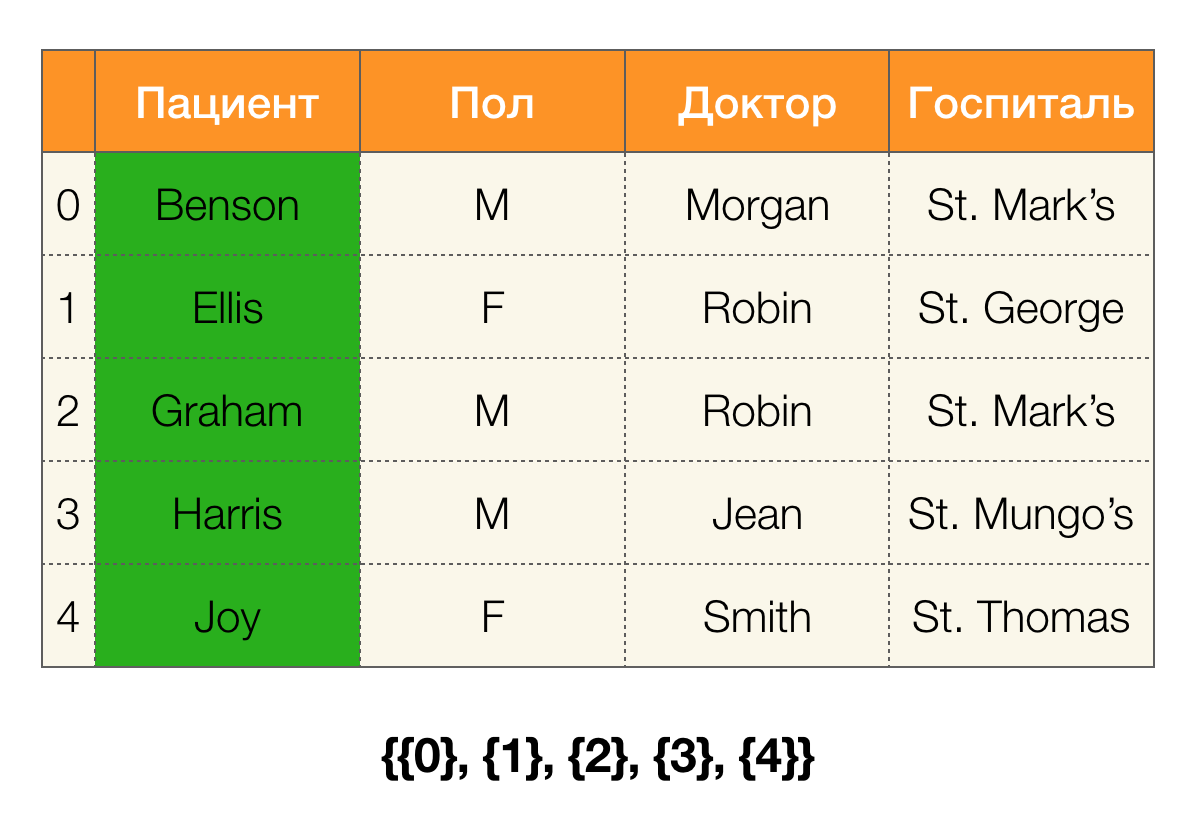
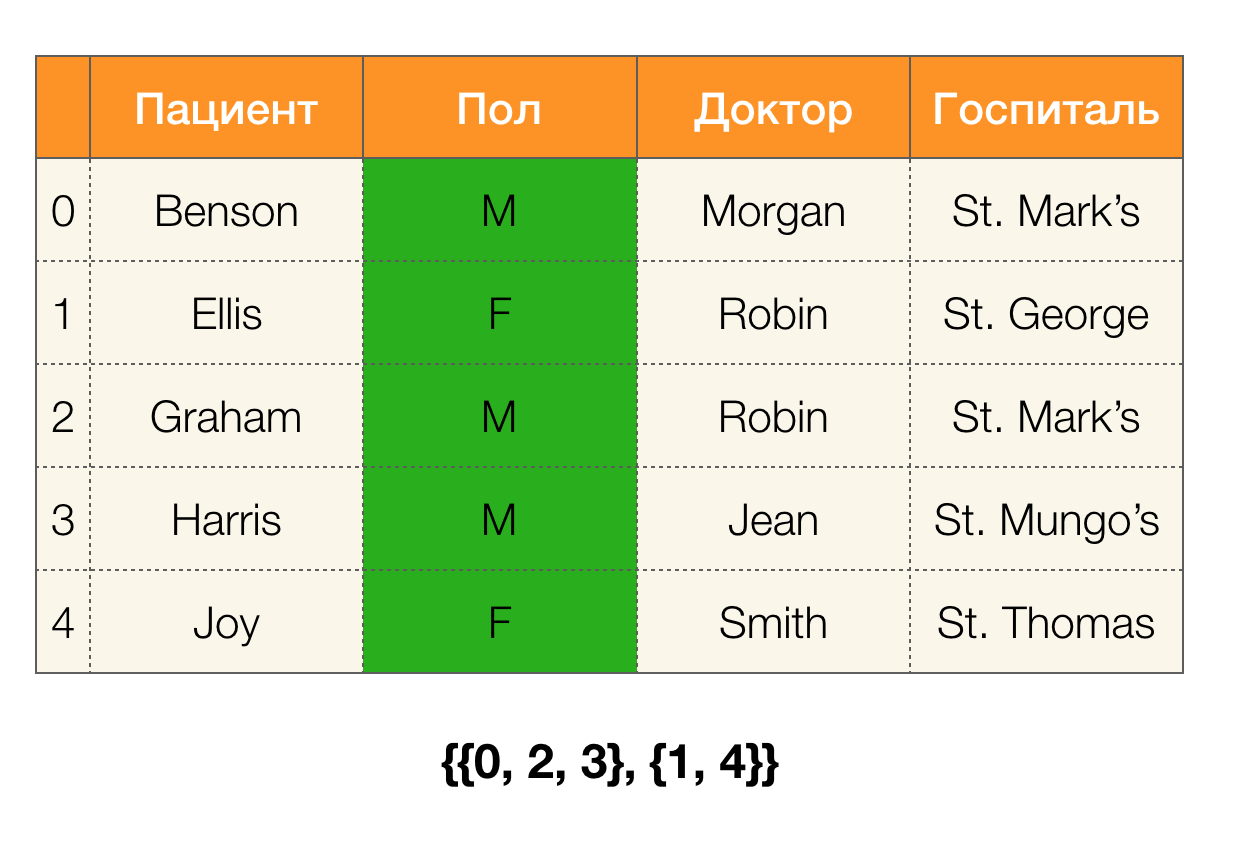
De plus, selon la définition, la partition de la colonne Patient sera en fait vide, car les clusters uniques sont exclus de la partition.

Les partitions peuvent être obtenues par plusieurs attributs. Et pour cela, il y a deux façons: parcourir la table, créer une partition à la fois selon tous les attributs nécessaires, ou la construire en utilisant le croisement de partitions le long d'un sous-ensemble d'attributs. Les algorithmes de recherche FZ utilisent la deuxième option.

En termes simples, par exemple, pour obtenir une partition par des colonnes ABC , vous pouvez prendre des partitions pour AC et B (ou tout autre ensemble de sous-ensembles disjoints) et les intersecter. L'opération d'intersection de deux partitions identifie les clusters de la plus grande longueur commune aux deux partitions.

Regardons un exemple:





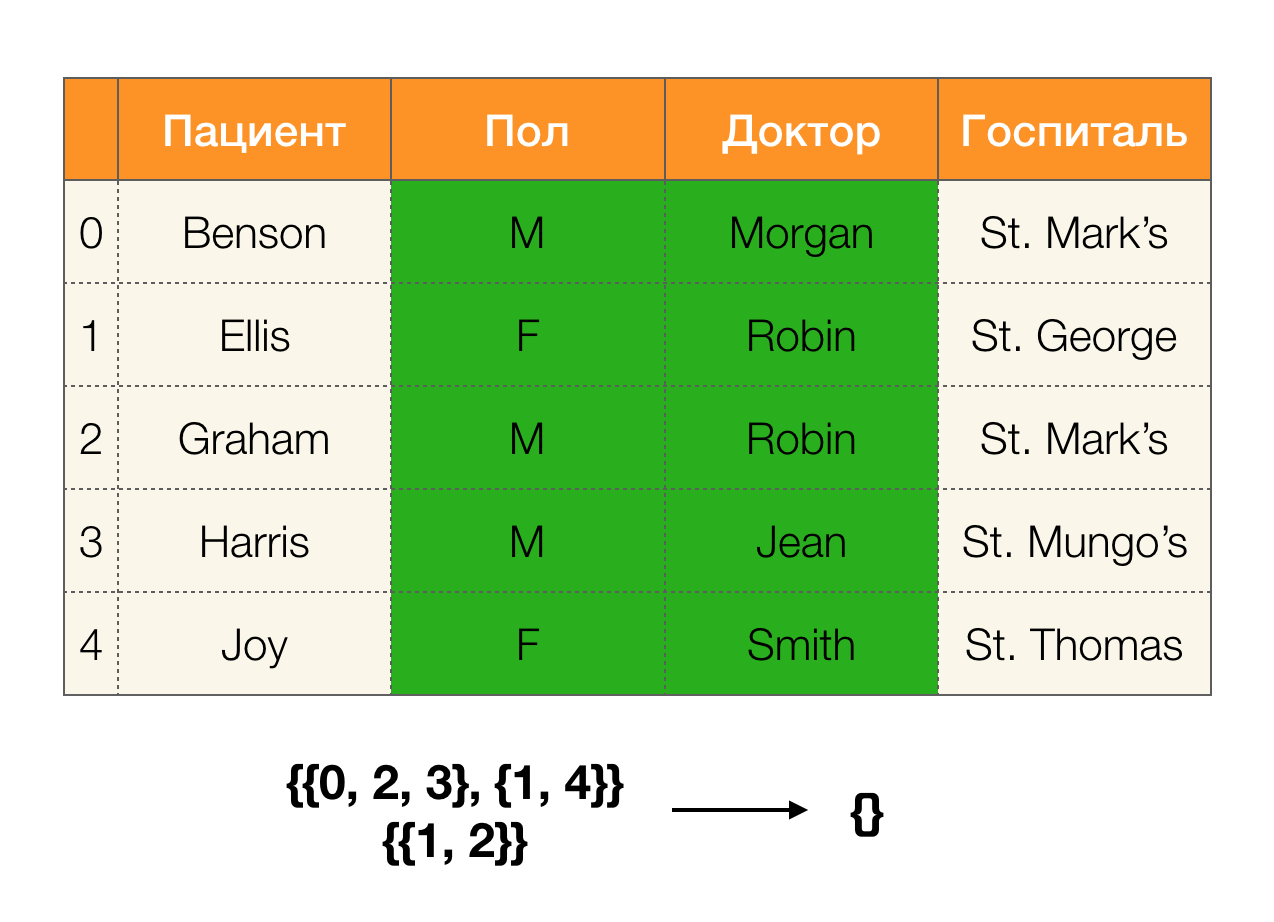
Dans le premier cas, nous avons reçu une partition vide. Si vous regardez attentivement le tableau, alors en effet, les valeurs identiques pour les deux attributs ne sont pas là. Si nous modifions légèrement le tableau (le cas à droite), nous obtenons déjà une intersection non vide. En même temps, les lignes 1 et 2 contiennent vraiment les mêmes valeurs pour les attributs Paul et Doctor .

Ensuite, nous avons besoin d'un concept tel que la taille de la partition. Formellement:

$$

$$| \ pi (X) | = | \ {c \ in \ pi (X): | c | > 1 \} |$$

Autrement dit, la taille de la partition est le nombre de clusters inclus dans la partition (rappelez-vous que les clusters individuels ne sont pas inclus dans la partition!):





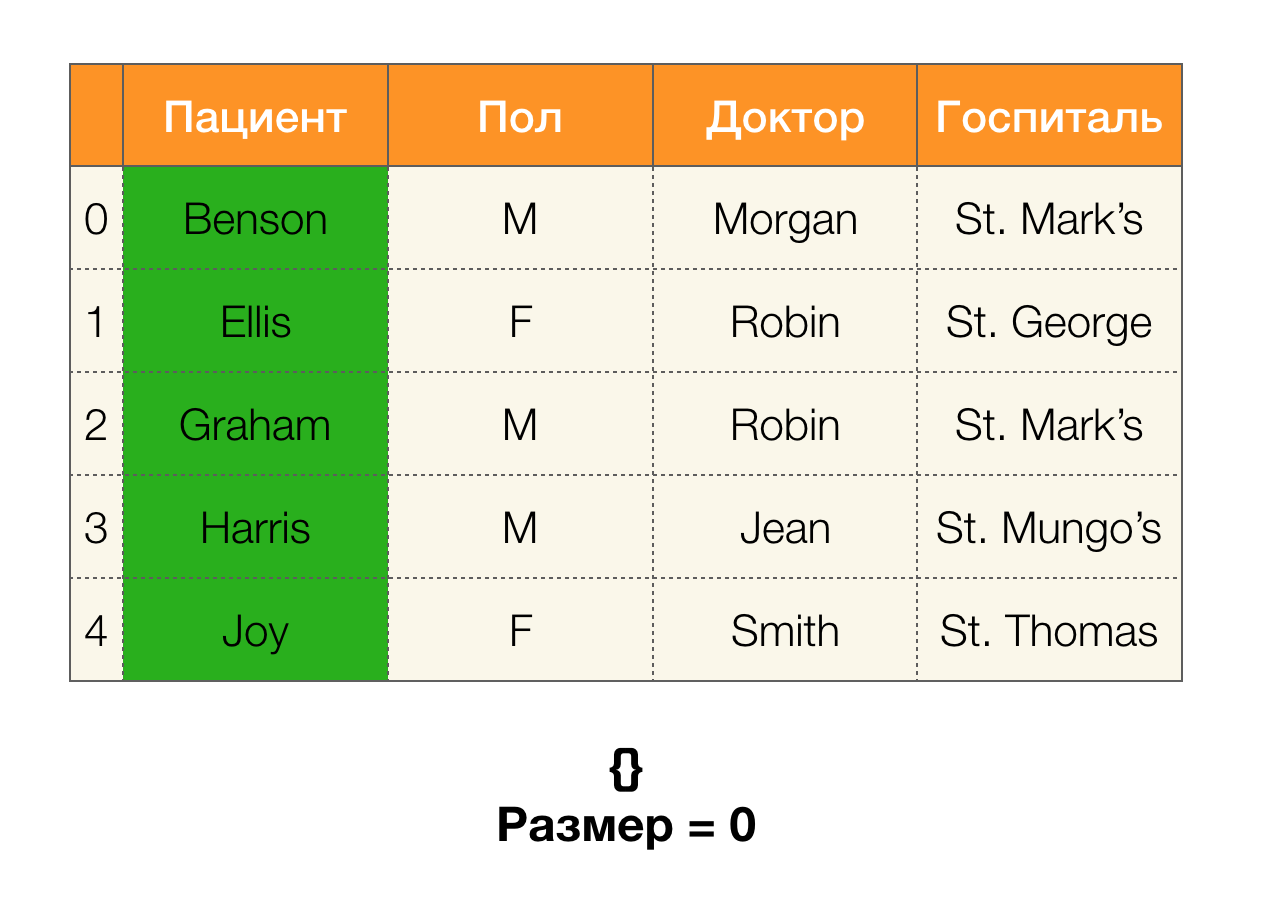
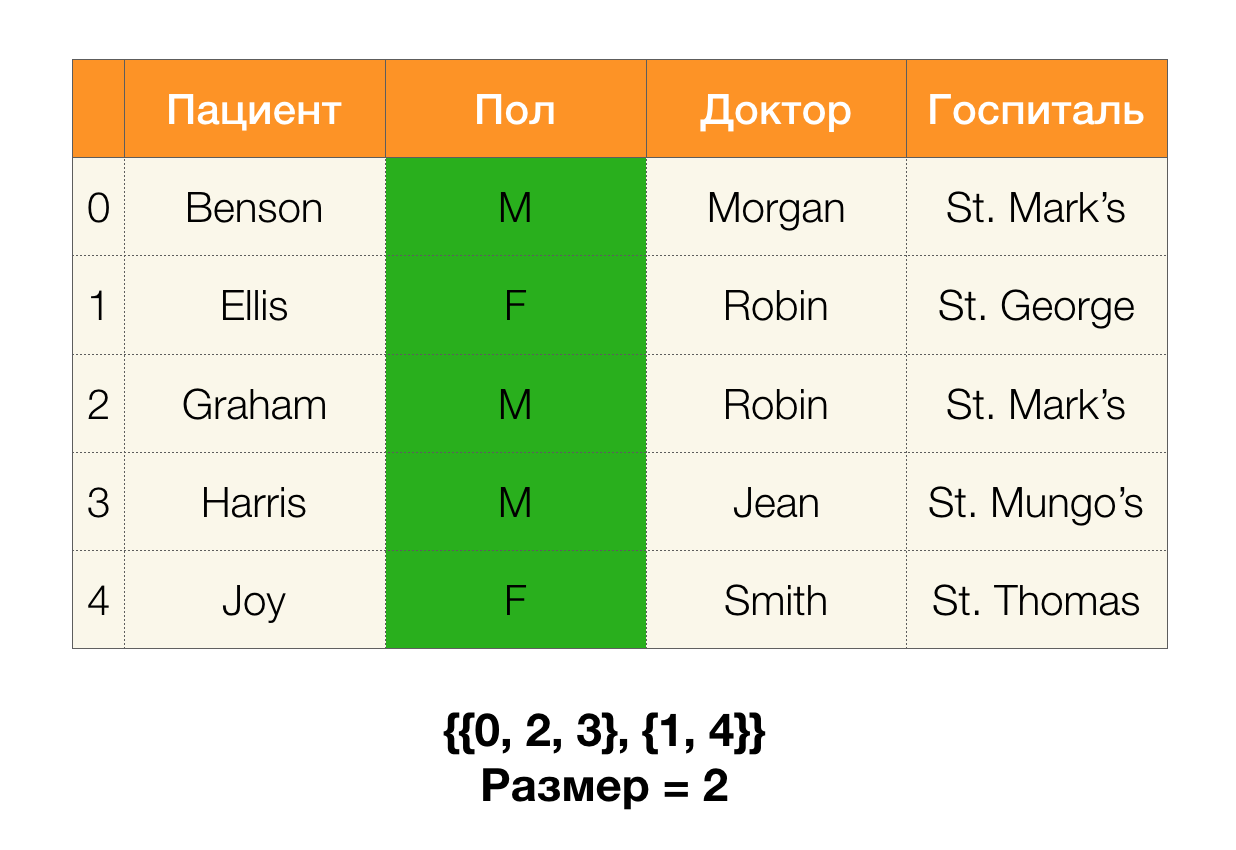
Maintenant, nous pouvons définir l'un des lemmes clés, qui pour des partitions données nous permet d'établir si la dépendance est maintenue ou non:

Lemme 1 . La dépendance A, B → C est maintenue si et seulement si

$$

$$| \ pi (AB) | = | \ pi (AB \ cup \ {C \}) |$$

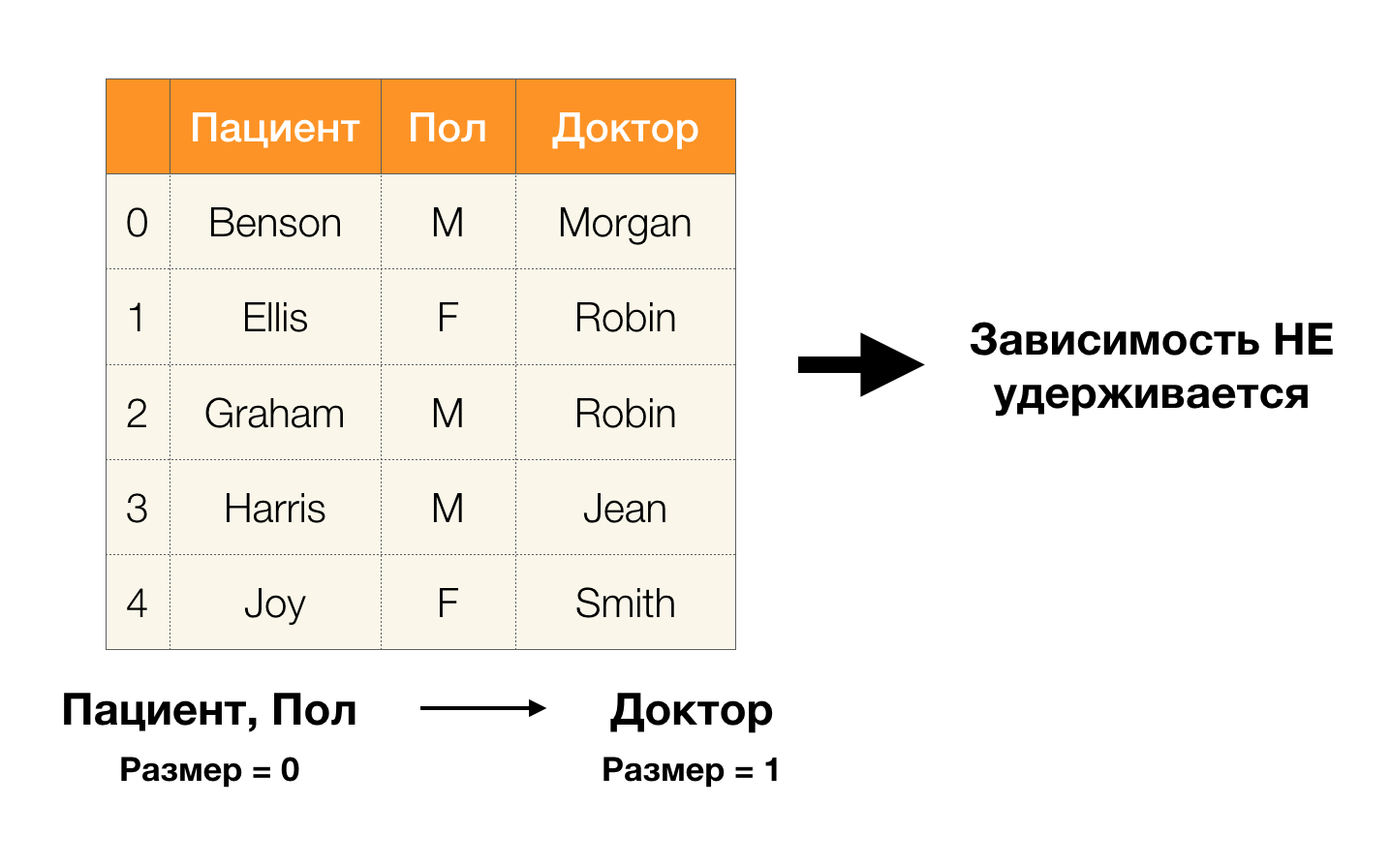
Selon le lemme, pour déterminer si une dépendance est maintenue, il est nécessaire d'effectuer quatre étapes:

1. Calculer la partition pour le côté gauche de la dépendance
2. Calculez la partition pour le côté droit de la dépendance
3. Calculez le produit des première et deuxième étapes
   
4. Comparer les tailles de partitions obtenues lors des première et troisième étapes
   

Voici un exemple de vérification si la dépendance est maintenue par ce lemme:






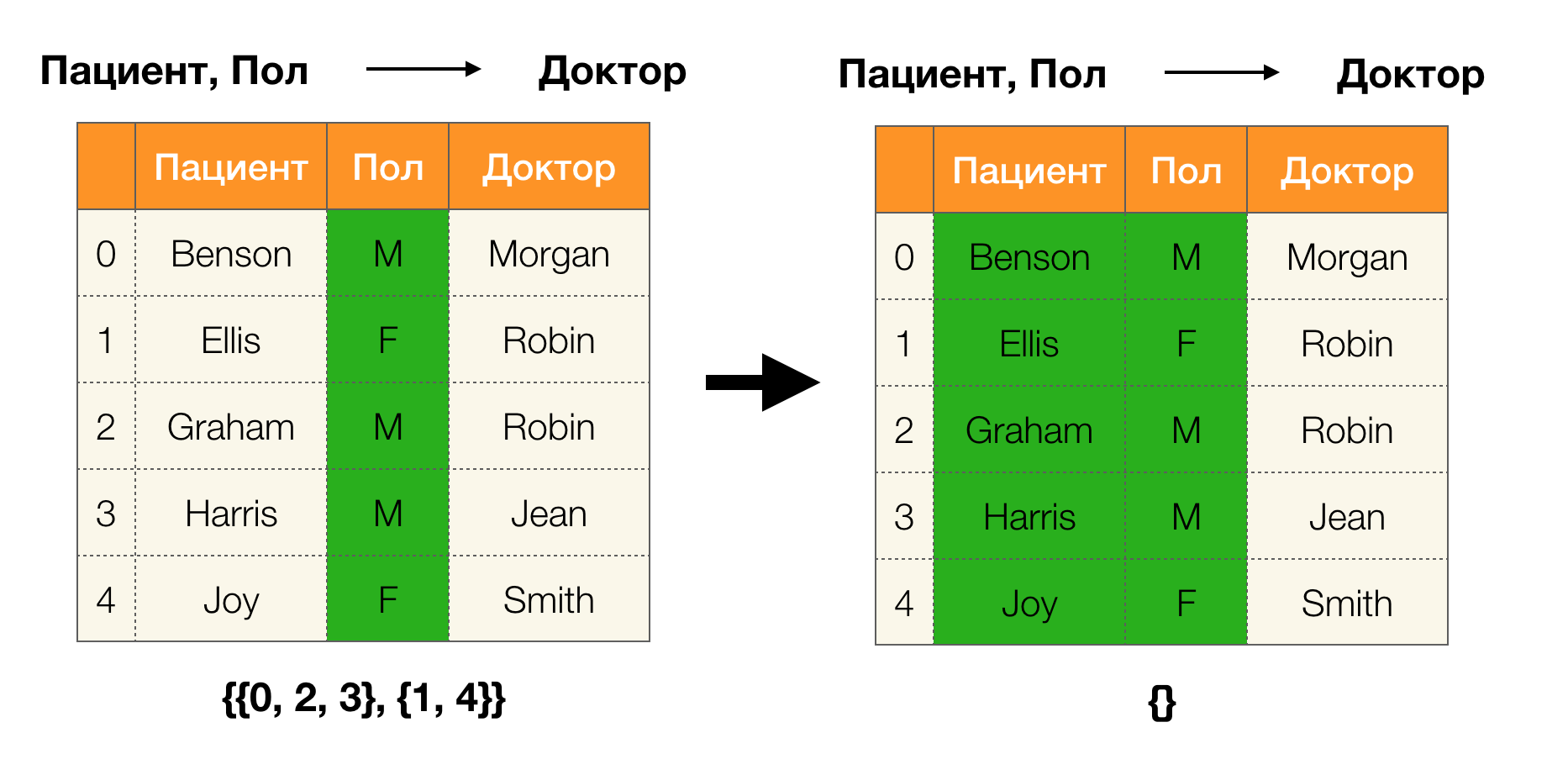
Dans cet article, nous avons examiné des concepts tels que la dépendance fonctionnelle, la dépendance fonctionnelle approximative, examiné où ils sont utilisés, ainsi que les algorithmes de recherche pour la loi fédérale. Nous avons également examiné en détail les concepts de base, mais importants, qui sont activement utilisés dans les algorithmes modernes de recherche de lois fédérales.

Références à la littérature:

1. Huhtala Y. et al. TANE: Un algorithme efficace pour découvrir les dépendances fonctionnelles et approximatives // Le journal informatique. - 1999. - T. 42. - Non. 2. - Art. 100-111.
2. Kruse S., Naumann F. Découverte efficace de dépendances approximatives // Actes de la dotation VLDB. - 2018. - T. 11. - Non. 7. - Art. 759-772.
3. Papenbrock T., Naumann F. Une approche hybride de la découverte de la dépendance fonctionnelle // Actes de la Conférence internationale de 2016 sur la gestion des données. - ACM, 2016 .-- S. 821-833.
4. Papenbrock T. et al. Découverte de la dépendance fonctionnelle: une évaluation expérimentale de sept algorithmes // Actes de la dotation VLDB. - 2015. - T. 8. - Non. 10. - Art. 1082-1093.
5. Kumar A. et al. Rejoindre ou ne pas rejoindre?: Réfléchir à deux fois sur les jointures avant la sélection des fonctionnalités // Actes de la Conférence internationale de 2016 sur la gestion des données. - ACM, 2016 .-- S. 19-34.
6. Abo Khamis M. et al. Apprentissage en base de données avec des tenseurs clairsemés // Actes du 37e Symposium ACM SIGMOD-SIGACT-SIGAI sur les principes des systèmes de bases de données. - ACM, 2018 .-- S. 325-340.
7. Hellerstein JM et al. La bibliothèque d'analyse MADlib: ou compétences MAD, le SQL // Proceedings of the VLDB Endowment. - 2012. - T. 5. - Non. 12. - Art. 1700-1711.
8. Qin C., Rusu F. Approximations spéculatives pour l'optimisation de la descente de gradient distribué terascale // Actes du quatrième atelier sur l'analyse des données dans le cloud. - ACM, 2015 .-- S. 1.
9. Meng X. et al. Mllib: Apprentissage automatique dans une étincelle apache // The Journal of Machine Learning Research. - 2016. - T. 17. - Non. 1 .-- S. 1235-1241.

Auteurs de l'article: Anastasia Birillo , chercheuse à JetBrains Research , étudiante au centre CS et Nikita Bobrov , chercheuse à JetBrains Research