Analyse détaillée de la méthode simplex

Prologue

Récemment, il était nécessaire de créer un programme à partir de zéro qui implémente l'algorithme de la méthode simplex. Mais au cours de la solution, j'ai rencontré un problème: il n'y a pas tellement de ressources sur Internet où vous pouvez consulter une analyse théorique détaillée de l'algorithme (sa justification: pourquoi nous prenons telle ou telle étape) et des conseils pratiques de mise en œuvre - directement, l'algorithme. Ensuite, je me suis fait une promesse - dès que j'aurai terminé la tâche, j'écrirai mon article sur ce sujet. En fait, nous en parlerons.

Remarque. La publication sera rédigée dans un langage assez formel, mais sera accompagnée de commentaires, qui devraient apporter une certaine clarté. Un tel format préservera l'approche scientifique et, en même temps, pourra aider certains dans l'étude de cette question.

§1. Énoncé du problème de programmation linéaire

Définition: La programmation linéaire est une discipline mathématique consacrée à la théorie et aux méthodes de résolution de problèmes extrêmes sur des ensembles d'espace à n dimensions définis par des systèmes d'équations linéaires et d'inégalités.

La tâche générale de la programmation linéaire (ci-après - LP) a la forme:

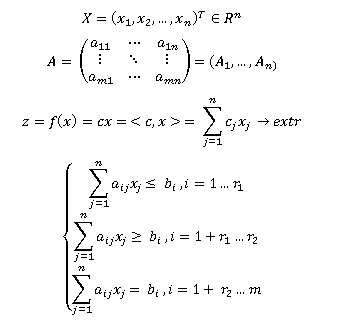
§2. La forme canonique du problème LP

La forme canonique du problème LP:



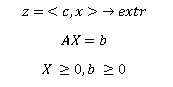Remarque: Tout problème LP se réduit à canonique.

L'algorithme pour la transition d'un problème LP arbitraire à la forme canonique:

1. Inégalités négatives$$ $ inline $ b_i $ inline $ multipliez par (-1).
2. Si une inégalité de la forme (≤), ajoutez à gauche$$ $ inline $ s_i $ inline $ Est une variable supplémentaire, et nous obtenons l'égalité.
3. Si une inégalité de la forme (≥), soustrayez du côté gauche$$ $ inline $ s_i $ inline $ , et nous obtenons l'égalité.
4. Nous faisons le remplacement des variables:

• Si$$ $ en ligne $ x_i ≤ 0 $ en ligne $ alors$$ $ inline $ x_i '= -x_i ≥ 0 $ inline $
• Si$$ $ en ligne $ x_i $ en ligne $ - tout$$ $ inline $ x_i = x_i '- x_i' '$ inline $ où$$ $ inline $ x_i ', x_i''≥ 0 $ inline $

Remarque: nous numérotons$$ $ inline $ s_i $ inline $ par le nombre d'inégalité auquel nous l'avons ajouté.

Remarque:$$ $ inline $ s_i $ inline $ ≥0.

§3. Points de coin. Variables de base / libres. Solutions basiques

Définition: point$$ $ en ligne $ X ∈ D $ en ligne $ appelé point d'angle si la représentation$$ $ en ligne $ X = αX ^ 1 + (1-α) X ^ 2, où X ^ 1, X ^ 2 ∈ D; 0 <α <1 $ en ligne $ uniquement possible avec$$ $ en ligne $ X ^ 1 = X ^ 2 $ en ligne $ .

En d'autres termes, il est impossible de trouver deux points dans la région, l'intervalle passant par qui contient$$ $ en ligne $ X $ en ligne $ (c.-à-d.$$ $ en ligne $ X $ en ligne $ N'est pas un point interne).

La méthode graphique de résolution du problème LP montre que la recherche de la solution optimale est associée à un point d'angle. C'est le concept de base lors du développement d'une méthode simplex.

Définition: Soit un système de m équations et n inconnues (m <n). Nous divisons les variables en deux ensembles: (nm) nous fixons les variables égales à zéro, et les m variables restantes sont déterminées en résolvant le système d'équations initiales. Si cette solution est unique, alors les variables non nulles sont appelées basiques; zéro (nm) variables - libres (non basiques), et les valeurs résultantes correspondantes des variables sont appelées la solution de base.

§4. Méthode simplex

La méthode simplex vous permet de trouver efficacement la solution optimale, en évitant l'énumération simple de tous les points d'angle possibles. Le principe principal de la méthode: les calculs commencent par une sorte de solution de base «de départ», puis une recherche est effectuée pour trouver des solutions qui «améliorent» la valeur de la fonction objectif. Cela n'est possible que si une augmentation de certaines variables entraîne une augmentation de la valeur de la fonctionnelle.

Prérequis pour appliquer la méthode simplex:

1. La tâche doit avoir une forme canonique.
2. La tâche doit avoir une base explicite.

Définition: Une base explicitement sélectionnée est un vecteur de la forme:$$ $ en ligne $ (.. 0100 ..) ^ T, (..010 ..) ^ T, (.. 0010 ..) ^ T ... $ en ligne $ , c'est-à-dire une seule coordonnée du vecteur est non nulle et égale à 1.

Remarque: Le vecteur de base a une dimension (m * 1), où m est le nombre d'équations dans le système de contraintes.

Pour faciliter les calculs et la visualisation, les tables simplex sont généralement utilisées:

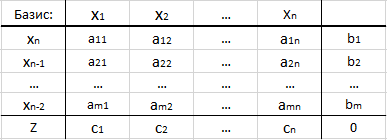
• La première ligne indique le "nom" de toutes les variables.
• Dans la première colonne, les numéros des variables de base sont indiqués, et dans la dernière cellule, la lettre Z (c'est la ligne fonctionnelle).
• Au "milieu du tableau", indiquez les coefficients de la matrice de contraintes - aij.
• La dernière colonne est le vecteur du côté droit des équations correspondantes du système de contraintes.
• La cellule la plus à droite est la valeur de la fonction objectif. À la première itération, il est supposé être 0.

Remarque: Les bases sont des variables, des coefficients dans la matrice des contraintes qui forment des vecteurs de base.

Remarque: Si les contraintes du problème d'origine sont représentées par des inégalités de la forme ≤, alors lorsque le problème est réduit à la forme canonique, les variables supplémentaires introduites forment la solution de base initiale.

Remarque: Les coefficients de la ligne fonctionnelle sont pris avec le signe «-».

Algorithme de méthode simplex:

1. Choisissez une variable que nous introduirons dans la base. Cela se fait selon le principe indiqué précédemment: il faut choisir une variable dont l'augmentation entraînera une augmentation de la fonctionnelle. La sélection se fait selon la règle suivante:

• Si la tâche est au minimum, sélectionnez l'élément positif maximum dans la dernière ligne.
• Si la tâche est au maximum, sélectionnez le négatif minimum.

Un tel choix correspond en effet au principe évoqué ci-dessus: si la tâche est au minimum, alors plus le nombre que l'on soustrait est grand, plus la fonction diminue rapidement; pour le maximum, au contraire - plus le nombre est élevé, plus la fonctionnalité grandit rapidement.

Remarque: Bien que nous prenions le nombre négatif minimum dans le problème au maximum, ce coefficient montre le sens de croissance de la fonctionnelle, car la ligne fonctionnelle dans la table simplex est prise avec le signe «-». Une situation similaire avec minimisation.

Définition: Une colonne d'une table simplex correspondant à un coefficient sélectionné est appelée colonne de tête .

2. Choisissez une variable que nous introduirons dans la base. Pour ce faire, vous devez déterminer laquelle des variables de base est la plus susceptible de disparaître lorsque la nouvelle variable de base se développe. Algébriquement, cela se fait comme suit:

• Le vecteur des parties de droite est divisé par la colonne de fin
• Parmi les valeurs obtenues, choisissez le minimum positif (les réponses négatives et nulles ne sont pas prises en compte)

Définition: Une telle ligne est appelée ligne de tête et correspond à une variable à dériver de la base.

Remarque: En fait, nous exprimons les anciennes variables de base de chaque équation du système de contraintes à travers le reste des variables et voyons dans quelle équation l'augmentation de la nouvelle variable de base donnera probablement 0. Entrer dans cette situation signifie que nous sommes «tombés» sur un nouveau sommet. C'est pourquoi les éléments zéro et négatifs ne sont pas pris en compte, car L'obtention d'un tel résultat signifie que le choix d'une telle nouvelle variable de base nous éloignera de la zone au-delà de laquelle il n'y a pas de solutions.

3. Nous recherchons un élément situé à l'intersection de la première ligne et de la colonne.

Définition: Un tel élément est appelé élément principal .

4. Au lieu de la variable à exclure, dans la première colonne (avec les noms des variables de base), écrivez le nom de la variable que nous entrons dans la base.

5. Ensuite, le processus de calcul d'une nouvelle solution de base commence. Cela se produit en utilisant la méthode Jordan-Gauss .

• Nouvelle ligne de plomb = Ancienne ligne de plomb / plomb
• Nouvelle ligne = Nouvelle ligne - Facteur de ligne dans la colonne de tête * Nouvelle ligne de tête

Remarque: Une conversion de ce type vise à introduire la variable sélectionnée dans la base, c'est-à-dire représentation de la colonne de tête comme vecteur de base.

6. Après cela, nous vérifions la condition d'optimalité. Si la solution résultante n'est pas optimale, répétez à nouveau tout le processus.

§5. Interprétation du résultat de la méthode simplex

1. Optimalité

La condition d'optimalité pour la solution résultante:

• Si la tâche est au maximum, il n'y a pas de coefficients négatifs dans la ligne fonctionnelle (c'est-à-dire qu'avec tout changement dans les variables, la valeur de la fonction résultante n'augmentera pas).
• Si la tâche est au minimum, il n'y a pas de coefficients positifs dans la ligne fonctionnelle (c'est-à-dire qu'avec tout changement dans les variables, la valeur de la fonction résultante ne diminuera pas).

2. Fonctionnalité illimitée

Cependant, il convient de noter qu'une fonction donnée peut ne pas atteindre un maximum / minimum dans une zone donnée. L'attribut algébrique de ceci peut être formulé comme suit:

Lors du choix d'une ligne de tête (variable à exclure), le résultat de la division terminale du vecteur de droite par la colonne de tête ne contient que des valeurs nulles et négatives.

En fait, cela signifie que quelle que soit la croissance que nous fixons une nouvelle variable de base, nous ne trouverons jamais de nouveau sommet. Notre fonction ne se limite donc pas à l'ensemble des solutions réalisables.

3. Solutions alternatives

Lors de la recherche de la solution optimale, une autre option est possible - il existe des solutions alternatives (un autre point d'angle qui donne la même valeur de la fonctionnalité).

Signe algébrique de l'existence d'une alternative:

Une fois la solution optimale atteinte, il n'y a plus de coefficients pour les variables libres dans la ligne fonctionnelle.

Cela signifie qu'avec la croissance de la variable correspondante avec un coefficient nul, la valeur de la fonctionnelle ne changera pas et une nouvelle solution de base donnera également l'optimum de la fonctionnelle.

Épilogue

Cet article vise à approfondir la compréhension de la partie théorique. Dans les commentaires et explications ici, vous pouvez obtenir des réponses aux questions qui sont généralement omises lors de l'étude de cette méthode et prises a priori. Cependant, il faut comprendre que de nombreuses méthodes d'optimisation numérique sont basées sur la méthode simplex (par exemple, la méthode Gomori , la méthode M ) et sans une compréhension fondamentale, il est peu probable que beaucoup de progrès puissent être réalisés dans l'étude et l'application de tous les algorithmes de cette classe.

Un peu plus tard, j'écrirai un article sur la mise en œuvre pratique de la méthode simplex, ainsi que plusieurs articles sur la méthode des variables artificielles (méthode M), la méthode Gomori et la méthode des branches et des bordures.

Merci de votre attention!

PS

Si vous êtes déjà tourmenté par la mise en œuvre de la méthode simplex, je vous conseille de lire le livre de A. Taha. Introduction à l'étude des opérations - tout y est bien analysé, tant en théorie qu'en exemples; et regardez également des exemples de résolution de problèmes matburo.ru - cela vous aidera à l'implémentation dans le code.