Livre d'Alan Turing et note mystérieuse - Détective scientifique

Traduction originale dans mon blog

Comment ce livre m'est-il arrivé?

En mai 2017, j'ai reçu un e-mail de mon ancien professeur de lycée nommé George Rutter, dans lequel il écrivait: « J'ai une copie du grand livre allemand de Dirac (Die Prinzipien der Quantenmechanik), qui appartenait à Alan Turing, et par la suite en lisant votre livre Idea Makers , il me semblait acquis que vous êtes la personne qui en a besoin . " Il m'a expliqué qu'il avait reçu un livre d'un autre (à ce moment-là décédé) mon professeur d'école Norman Rutledge , dont je savais qu'il était un ami d'Alan Turing. George a conclu sa lettre par la phrase: " Si vous avez besoin de ce livre, je pourrais vous le remettre la prochaine fois que vous viendrez en Angleterre ."

Après quelques années en mars 2019, je suis vraiment arrivé en Angleterre, après quoi j'ai convenu avec George de me retrouver pour le petit déjeuner dans un petit hôtel à Oxford. Nous avons mangé, bavardé et attendu que la nourriture se stabilise. Puis vint le bon moment pour discuter du livre. George mit sa main dans sa mallette et en sortit un volume académique typique plutôt modeste du milieu des années 1900.



J'ai ouvert la couverture, me demandant si cela pouvait être au dos de l'inscription: "La Propriété d'Alan Turing" ou quelque chose comme ça. Mais, malheureusement, ce n'était pas le cas. Néanmoins, une note suffisamment expressive sur quatre feuilles de Norman Rutledge à George Rutter, écrite en 2002, y était jointe.

J'ai connu Norman Rutledge lorsque j'étais encore lycéen à Eton au début des années 1970. Il était professeur de mathématiques surnommé The Nutty Norman. Il était un enseignant agréable à tous égards et racontait des histoires sans fin sur les mathématiques et toutes sortes d'autres choses intéressantes. Il était responsable de veiller à ce que l'école reçoive un ordinateur (programmé avec du ruban perforé de la largeur d'un bureau) - c'était le tout premier ordinateur que j'aie jamais utilisé .

À cette époque, je ne savais rien du passé de Norman (rappelez-vous que c'était bien avant l'avènement d'Internet). Je savais seulement qu'il était "Dr. Rutledge". Il racontait souvent des histoires de gens de Cambridge, mais dans ses histoires, il n'a jamais mentionné Alan Turing. Bien sûr, Turing n'était pas assez célèbre à l'époque (même si, en fait, j'ai déjà entendu parler de lui par quelqu'un qui le connaissait à Bletchley Park (le manoir dans lequel le centre de cryptage était situé pendant la Seconde Guerre mondiale)).

Alan Turing n'est devenu célèbre qu'en 1981, lorsque j'ai commencé à étudier des programmes simples , bien qu'à l'époque dans le contexte des automates cellulaires, et non des machines Turing .

Soudain, un jour, en regardant un catalogue de cartes dans la bibliothèque du California Institute of Technology , je suis tombé sur le livre Alan M. Turing , écrit par sa mère Sarah Turing. Le livre contenait beaucoup d'informations, y compris les travaux scientifiques inédits de Turing sur la biologie. Cependant, je n'ai rien appris de sa relation avec Norman Rutledge, car le livre ne mentionnait rien de lui (bien que, comme je l'ai découvert, Sarah Turing ait correspondu avec Norman à propos de ce livre , et Norman a même écrit une critique à la fin).



Dix ans plus tard, à l'écoute de Turing et de son travail de biologie (alors non publié), j'ai visité les archives de Turing au King's College de Cambridge . Bientôt, après m'être familiarisé avec ce qu'ils avaient du travail de Turing et y avoir passé un peu de temps, j'ai pensé qu'en même temps je pouvais lui demander de voir également sa correspondance personnelle. En le parcourant, j'ai trouvé plusieurs lettres d'Alan Turing à Norman Rutledge.

À ce moment-là, la biographie d' Andrew Hodges a été publiée, ce qui a fait en sorte que Turing est finalement devenu célèbre, cela a confirmé qu'Alan Turing et Norman Rutledge étaient vraiment amis, et aussi que Turing était un consultant scientifique de Norman. Je voulais poser des questions à Rutledge sur Turing, mais Norman était déjà à la retraite et menait une vie isolée. Cependant, quand j'ai terminé le travail sur le livre A New Kind of Science en 2002 (après ma retraite de dix ans), je l'ai retrouvé et lui ai envoyé une copie du livre avec la légende, «To My Last Math Teacher». Ensuite, nous avons correspondu un peu, et en 2005, je suis de nouveau venu en Angleterre et j'ai accepté de rencontrer Norman pour une tasse de thé dans un hôtel de luxe au centre de Londres.

Nous avons eu une belle discussion sur beaucoup de choses, y compris Alan Turing. Norman a commencé notre conversation avec l'histoire qu'il connaissait vraiment Turing, surtout superficiellement, il y a 50 ans. Mais néanmoins, il avait quelque chose à dire sur lui personnellement: " Il était insociable ". " Il a beaucoup ri ." " Il ne pouvait pas vraiment parler avec les non-mathématiciens ." " Il avait toujours peur de bouleverser sa mère ." " Il est parti pendant la journée et a couru un marathon ." " Il n'était pas trop ambitieux ." Puis la conversation est revenue sur l'identité de Norman. Il a dit que malgré le fait qu'il avait déjà pris sa retraite depuis 16 ans, il écrit toujours des articles pour le Journal Mathématique , de sorte que, selon ses mots, "pour terminer tous ses travaux scientifiques avant de déménager dans un autre monde " , où, comme il l'a ajouté avec un sourire à peine perceptible, " toutes les vérités mathématiques seront certainement révélées ". À la fin du goûter, Norman enfila sa veste en cuir et se dirigea vers son cyclomoteur, ignorant complètement les explosions qui perturbèrent la circulation à Londres ce jour-là.

C'est la dernière fois que j'ai vu Norman, il est décédé en 2013.

Six ans plus tard, je me suis assis au petit déjeuner avec George Rutter. J'avais avec moi une note de Rutledge, écrite par lui en 2002 dans son écriture caractéristique:



Au début, j'ai lu la note couramment. Elle était expressive comme d'habitude:

J'ai reçu un livre d'Alan Turing de son ami et exécuteur testamentaire Robin Gandy (au King's College, il était normal de distribuer des livres de la collection de camarades décédés, et j'ai choisi la collection de poèmes d'AE Houseman des livres d' Ivor Ramsey comme cadeau approprié (il était le doyen et sauté de la chapelle [en 1956]) ...

Plus tard dans une courte note, il écrit:

Vous demandez où, à la fin, ce livre aurait dû aller - à mon avis, il devrait aller à quelqu'un qui apprécie tout ce qui concerne le travail de Turing, donc son sort dépend de vous.

Stephen Wolfram m'a envoyé son livre impressionnant, mais je n'y ai pas plongé assez profondément ...

En conclusion, il a félicité George Rutter d'avoir eu le courage de déménager (comme il s'est avéré, temporairement) en Australie après sa retraite, affirmant qu'il jouerait lui-même au Sri Lanka comme exemple d'une existence bon marché et semblable à celle d'un lotus. mais a ajouté que «les événements qui s'y déroulent indiquent maintenant qu'il n'aurait pas dû faire cela » (faisant apparemment référence à la guerre civile au Sri Lanka).

Alors qu'est-ce qui est caché dans les entrailles du livre?

Alors, qu'ai-je fait avec une copie d'un livre en langue allemande écrit par Paul Dirac qui appartenait autrefois à Alan Turing. Je ne lis pas l'allemand, mais j'avais une copie du même livre en anglais (qui est la langue de son original) de l'édition des années 1970. Néanmoins, une fois au petit déjeuner, il m'a semblé exact que je devais lire attentivement le livre page par page. En fin de compte, c'est une pratique courante lorsqu'il s'agit de livres anciens.

Il est à noter que j'ai été frappé par l'élégance de la présentation de Dirac. Le livre a été publié en 1931, mais son pur formalisme (et, oui, malgré la barrière de la langue, j'ai pu lire les mathématiques décrites dans le livre) est presque le même que s'il avait été écrit aujourd'hui. (Je ne veux pas trop me concentrer sur Dirac ici, mais mon ami Richard Feynman m'a dit que, du moins à son avis, l'exposition de Dirac est monosyllabique. Norman Rutledge m'a dit qu'il était ami à Cambridge avec le fils adoptif de Dirac , qui est devenu théoricien dans Norman était assez souvent dans la maison de Dirac et disait que le «grand homme» s’estompait parfois personnellement en arrière-plan, tandis que le premier plan avait toujours beaucoup de casse-tête mathématiques. Malheureusement, je n’ai moi-même jamais rencontré Paul Dirac, bien que On m'a dit qu'après t wow, comme il a finalement quitté Cambridge et est allé en Floride, il a perdu la plupart de son ancienne raideur et est devenu une personne assez sociable).

Mais revenons au livre de Dirac, qui appartenait à Turing. À la page 9, j'ai remarqué des soulignements et de petites notes de marge écrites au crayon simple. J'ai continué à feuilleter les pages. Après plusieurs chapitres, les notes ont disparu. Mais alors, tout d'un coup, j'ai trouvé une note intégrée à la page 127 avec le contenu suivant:



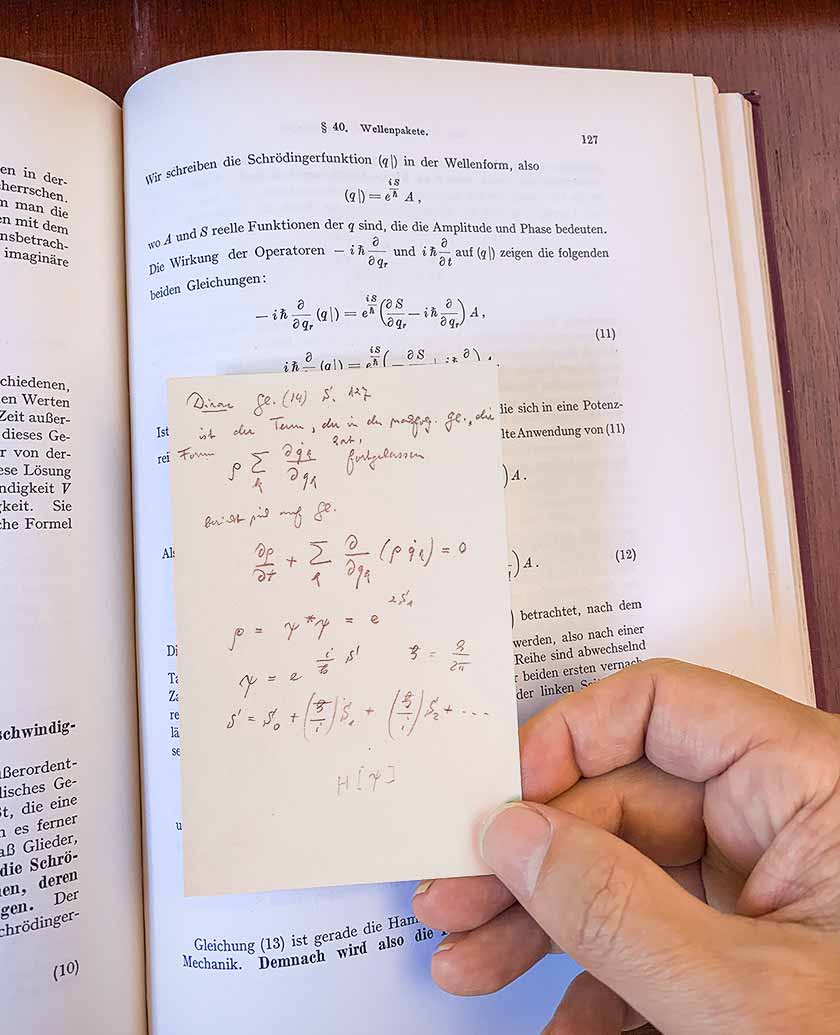
Il a été écrit en allemand avec une écriture allemande standard. Et il semble que cela pourrait être en quelque sorte lié à la mécanique lagrangienne . Je pensais que quelqu'un possédait probablement ce livre avant Turing, et ce doit être une note écrite par cette personne.

J'ai continué à feuilleter le livre. Pas de notes. Et je pensais que je ne pouvais plus rien trouver. Mais ensuite, à la page 231, j'ai trouvé le signet de la société - avec du texte imprimé:



Vais-je éventuellement trouver autre chose? J'ai continué à feuilleter le livre. Puis, à la fin du livre, à la page 259, dans la section sur la théorie relativiste des électrons, j'ai trouvé ce qui suit:



J'ai déplié cette feuille de papier:



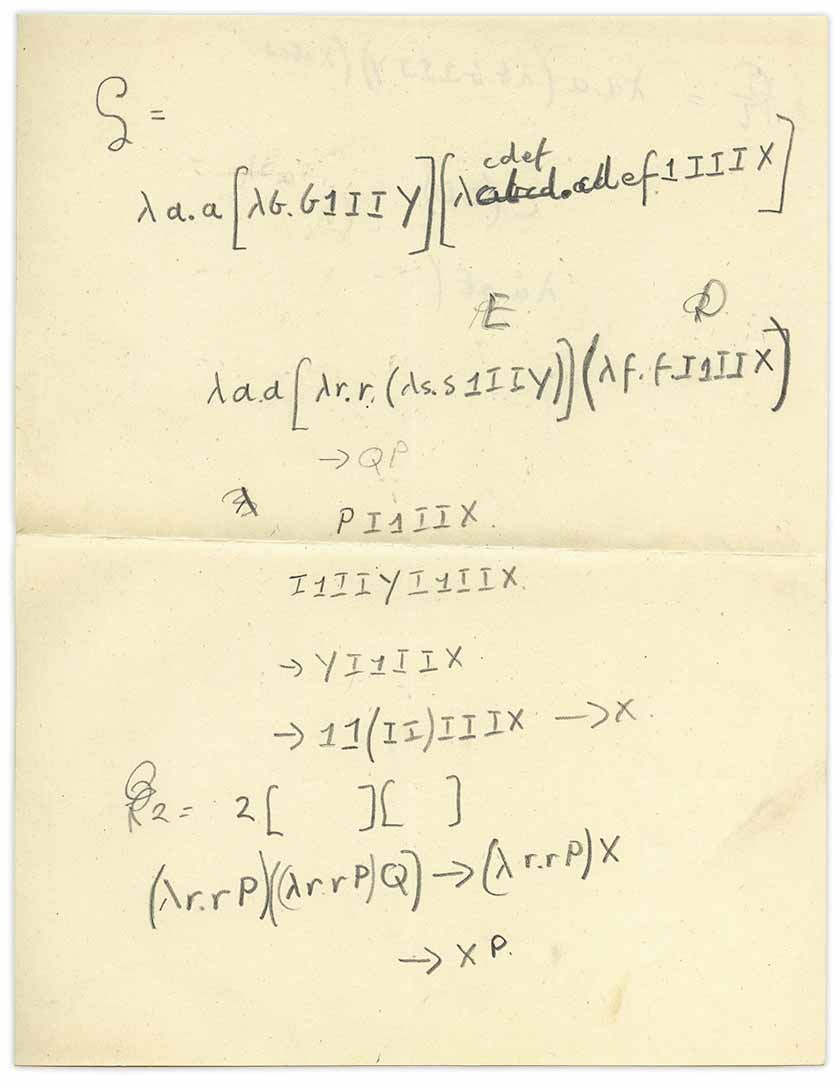
J'ai immédiatement réalisé qu'il s'agissait d'un calcul lambda avec un mélange de combinateurs , mais comment cette feuille est-elle apparue ici? Rappelons que ce livre est un livre sur la mécanique quantique, mais la feuille ci-jointe traite de la logique mathématique, ou de ce qu'on appelle maintenant la théorie du calcul. C'est typique des écrits de Turing. Je me demandais si Turing avait personnellement écrit cette note.

Même pendant le petit déjeuner, j'ai cherché sur Internet des échantillons d'écriture de Turing, mais je n'ai pas trouvé d'exemples sous forme de calculs, donc je n'ai pas pu tirer de conclusions sur l'identité exacte de l'écriture. Et bientôt j'ai dû partir. J'ai soigneusement emballé le livre, prêt à révéler le secret de la page et de son auteur, et je l'ai emporté avec moi.

À propos du livre

Tout d'abord, discutons du livre lui-même. Les principes de la mécanique quantique de Paul Dirac ont été publiés en anglais en 1930 et bientôt traduits en allemand. (La préface de Dirac est datée du 29 mai 1930; elle appartient au traducteur, Werner Bloch , le 15 août 1930.) Le livre est devenu une étape importante dans le développement de la mécanique quantique, établissant systématiquement un formalisme clair pour effectuer des calculs, et, entre autres choses, expliquant la prédiction de Dirac sur le positron , qui sera ouvert en 1932.

Pourquoi Alan Turing avait-il un livre en allemand, pas en anglais? Je ne le sais pas avec certitude, mais à cette époque, l'allemand était la principale langue de la science, et nous savons qu'Alan Turing a pu le lire. (Après tout, dans le titre de son célèbre travail de machine de Turing " À propos des nombres calculables avec une annexe au problème de résolution (Entscheidungsproblem) »était un très long mot allemand - et dans la partie principale de l'article, il opère avec des caractères gothiques assez obscurs sous la forme de« lettres allemandes », qu'il a utilisées à la place, par exemple, des caractères grecs).

Alan Turing a acheté le livre lui-même ou le lui a remis? Je ne sais pas. À l'intérieur de la couverture du livre de Turing, il y a une notation au crayon «20 / -», qui était la notation standard «20 shillings», similaire à 1 £. Sur la page de droite, il y a un «26.9.30» effacé, signifiant soi-disant le 26 septembre 1930 - peut-être la date à laquelle le livre a été acheté pour la première fois. Ensuite, dans le coin le plus à droite, le nombre effacé est "20". C'est peut-être encore le prix. (Serait-ce le prix dans les Reichsmarks , si nous supposons que le livre a été vendu en Allemagne? À cette époque, 1 Reichsmark valait environ 1 shilling, le prix allemand serait probablement écrit comme, par exemple, «20 RM».) Enfin, sur l'intérieur de la couverture arrière est "c 5 / -" - c'est peut-être (avec une grande remise) le prix d'un livre d'occasion.

Regardons les principales dates de la vie d'Alan Turing. Alan Turing est né le 23 juin 1912 (par coïncidence, exactement 76 ans avant Mathematica 1.0 ). À l'automne 1931, il entre au King's College de Cambridge. Il a obtenu son baccalauréat après les trois années d'études standard, en 1934.

Dans les années 1920 et au début des années 1930, la mécanique quantique était un sujet brûlant, et Alan Turing s'y intéressait certainement. Nous savons par ses archives qu'en 1932, dès la publication du livre, il reçut les " Fondements mathématiques de la mécanique quantique " de John von Neumann (en allemand ). Nous savons également qu'en 1935 Turing a reçu une tâche du physicien de Cambridge Ralph Fowler au sujet de l'étude de la mécanique quantique. (Fowler a proposé de calculer la constante diélectrique de l'eau , ce qui est en fait une tâche très difficile, nécessitant une analyse complète avec la théorie du champ quantique en interaction, qui n'est toujours pas complètement résolue).

Et pourtant, quand et comment Turing a-t-il obtenu son exemplaire du livre de Dirac? Étant donné que le livre a un prix cassé, Turing l'aurait acheté déjà utilisé. Qui était le premier propriétaire du livre? Les notes du livre semblent se rapporter principalement à la structure logique, il est à noter qu'une certaine relation logique devrait être considérée comme un axiome. Qu'en est-il alors de la note jointe à la page 127?

Eh bien, cela peut être une coïncidence, mais juste à la page 127 - Dirac parle du principe quantique de la moindre action et jette les bases d'une intégrale le long du chemin de Feynman - qui est la base de tout formalisme quantique moderne. Que contient la note? Il contient une extension de l'équation 14, qui est une équation pour l'évolution temporelle de l'amplitude quantique. L'auteur de la note a remplacé Dirac A pour l'amplitude par ρ, reflétant peut-être le record allemand antérieur (analogie de la densité des liquides). Ensuite, l'auteur essaie d'étendre l'action en puissances de ℏ (la constante de Planck divisée par 2π, qui est parfois appelée la constante de Dirac ).

Mais il semble que d'après ce qui est contenu sur la page, il y a peu de choses qui peuvent être apprises utiles. Si vous gardez la page à la lumière, elle contient une petite surprise - un filigrane avec l'inscription "Z f. Physik. Chem. B ”:



Il s'agit d'une version abrégée de Zeitschrift für physikalische Chemie, Abteilung B , la revue allemande de chimie physique, publiée depuis 1928. Peut-être que la note a été écrite par l'éditeur du journal? Voici le titre du magazine de 1933. Idéalement, les éditeurs sont répertoriés avec leur emplacement, et l'un d'eux se démarque: «Born · Cambridge».



C'est Max Bourne qui est l'auteur de la règle de Bourne et bien plus dans la théorie de la mécanique quantique (ainsi que le grand-père de la chanteuse Olivia Newton-John ). Donc, cette note a peut-être été écrite par Max Born? Mais, malheureusement, ce n'est pas le cas, car l'écriture ne correspond pas.

Qu'en est-il des signets à la page 231? La voici de deux côtés:



Le marque-page est bizarre et assez joli. Mais quand a-t-il été fabriqué? Il y a une librairie Heffers à Cambridge , bien qu'elle fasse maintenant partie de Blackwell. Pendant plus de 70 ans (jusqu'en 1970), Heffers a été localisé à l'adresse, comme le montre le signet, 3 et 4 par Petty Cury .

Cet onglet contient une clé importante - il s'agit du numéro de téléphone „Tél. 862. " Il s'est avéré qu'en 1939, la plupart de Cambridge (y compris Heffers) sont passés à des numéros à quatre chiffres et, bien sûr, en 1940, les signets ont été imprimés avec des numéros de téléphone "modernes". (Les numéros de téléphone en anglais ont progressivement augmenté; lorsque j'ai grandi en Angleterre dans les années 1960, nos numéros de téléphone étaient Oxford 56186 et Kidmore End 2378. En partie, je me souviens de ces numéros parce que, curieusement, c'est maintenant il n'avait pas l'air, j'ai toujours appelé mon numéro lorsque je répondais à un appel entrant).

Le signet sous cette forme a été imprimé jusqu'en 1939. Mais combien de temps avant ça? Vous pouvez trouver pas mal de scans d'anciennes publicités Heffers sur Internet, au moins depuis 1912 (avec «Nous vous demandons de satisfaire vos demandes ...»), ils ajoutent «Téléphone 862», ajoutant «(2 lignes)». Il existe également des signets avec un design similaire qui peuvent être trouvés dans les livres depuis 1904 (bien qu'il ne soit pas clair s'ils étaient originaux pour ces livres (c'est-à-dire imprimés en même temps). Aux fins de notre enquête, il semble que nous pouvons conclure que ce livre est venu de la boutique Heffers (qui était d'ailleurs la principale librairie de Cambridge) entre 1930 et 1939.

Page avec calcul lambda

Alors maintenant, nous savons quelque chose sur le moment où le livre a été acheté. Mais qu'en est-il de la «page de calcul lambda»? Quand est-ce écrit? Eh bien, bien sûr, d'ici là, le calcul lambda aurait dû être inventé. Et cela a été fait par Alonzo Church , un mathématicien de Princeton , dans sa forme originale en 1932 et dans sa forme finale en 1935. (Il y avait des travaux de scientifiques de leurs prédécesseurs, mais ils n'ont pas utilisé la notation λ).

Il existe une relation complexe entre Alan Turing et le calcul lambda. En 1935, Turing s'intéresse à la «mécanisation» des opérations mathématiques et invente l'idée d'une machine de Turing qui l'utilise pour résoudre les problèmes des fondements des mathématiques. Turing a envoyé un article à ce sujet au magazine français ( Comptes rendus ), mais il a été perdu par la poste; puis il s'est avéré que le destinataire auquel il l'avait envoyée n'était toujours pas là, puisqu'il avait déménagé en Chine.

Mais en mai 1936, avant même que Turing ne puisse envoyer son article ailleurs, l' œuvre d'Alonzo Church arriva des États-Unis .Turing s'était déjà plaint que lorsqu'il avait développé la preuve du théorème de la limite centrale en 1934, il avait découvert qu'un mathématicien norvégien avait déjà présenté la preuve en 1922.
Il est facile de comprendre que les machines de Turing et le calcul lambda sont en fait équivalents dans les types de calculs qu'ils peuvent représenter (et c'est le début de la thèse de Church-Turing ). Cependant, Turing (et son professeur Max Newman ) s'assurèrent que l'approche de Turing était suffisamment excellente pour mériter une publication séparée. En novembre 1936 (et avec des fautes de frappe corrigées le mois suivant) dans les écrits de la London Mathematical Society « …» .

: 1936 1938 ( 1937 ) , , . , -, — , - , — , , .

1938 , , -, , . 1945 , . 1947–8 , , .

1951 . ( , , , , - , ). , 1954 , : « » ( : « , »). , , 7 1954 , . ( , , .)

, -. , :



, , , . ? , , , Spalding&Hodge, Papermakers, « », - , -, . , , , Excelsior, , 1890- 1954 .

?

Alors, regardons de plus près ce qui se trouve des deux côtés de la feuille. Commençons par les lambdas.

Voici une façon de définir des fonctions «pures» ou «anonymes» , et elles sont le concept de base en logique mathématique, et maintenant en programmation fonctionnelle. Ces fonctions sont assez courantes dans Wolfram Language , et leur travail est assez facile à expliquer. Par exemple, quelqu'un écrit f [ x ] pour désigner la fonction f appliquée à l'argument x. Et il existe de nombreuses fonctions nommées f telles que Abs ou Sin ou Blur . Mais que se passe-t-il si quelqu'un veut que f [ x ] soit 2x +1 ? Il n'y a pas de nom immédiat pour cette fonction. Mais existe-t-il une autre forme d'affectation, f [ x ]?

La réponse est oui: au lieu de f, nous écrivons la Function[a,2a+1] . Et dans le langage de Function [a,2a+1][x] Wolfram Function [a,2a+1][x] applique des fonctions à l'argument x, ce qui donne 2x+1 en conséquence. Function[a,2a+1] est une fonction "pure" ou "anonyme", qui est une pure opération de multiplication par 2 et d'addition de 1.

Ainsi, λ dans le calcul lambda est un analogue exact de la fonction dans le langage Wolfram - et donc, par exemple, λ a. (2 a + 1) est équivalent à la Function[a, 2a + 1] . (Il convient de noter que la fonction, par exemple, la Function[b,2b+1] équivalente; les «variables liées» a ou b ne sont que des endroits pour remplacer l'argument de la fonction - et dans le langage Wolfram, elles peuvent être évitées en utilisant des options alternatives pour définir une fonction pure (2# +1)& ).

En mathématiques traditionnelles, les fonctions sont généralement considérées comme des objets qui affichent des données d'entrée (par exemple, des entiers) et des données de sortie (qui sont également, par exemple, des entiers). Mais quel est cet objet Function (ou λ)? Il s'agit essentiellement d'un opérateur structurel qui prend des expressions et les transforme en fonctions. Cela peut sembler un peu étrange en termes de mathématiques traditionnelles et de la forme mathématique de l'écriture, mais si quelqu'un a besoin de manipuler des caractères arbitraires, ce qui est beaucoup plus naturel, même si au début cela semble un peu abstrait. (Il convient de noter que lorsque les utilisateurs apprennent le Wolfram Language, je peux toujours dire qu'ils ont franchi un certain seuil de pensée abstraite lorsqu'ils ont une idée de la fonction ).

Les lambdas ne sont qu'une partie de ce qui est sur la page. Il existe un autre concept encore plus abstrait - ce sont les combinateurs . Considérez la ligne PI1IIx plutôt obscure? Qu'est-ce que cela signifie? En fait, il s'agit d'une séquence de combinateurs, ou d'une composition abstraite de fonctions symboliques.

La superposition habituelle de fonctions, assez familière en mathématiques, dans le Wolfram Language peut être écrite sous la forme: f[g[x]] - ce qui signifie "appliquer f au résultat de l'application de g à x ". Mais les supports sont-ils vraiment nécessaires pour cela? Dans Wolfram, f@g@ x est une autre forme de notation. Dans cet article, nous nous appuyons sur la définition de Wolfram Language: l'opérateur @ est associé au côté droit, donc f@g@x équivalent à f@(g@x) .

Mais que signifiera l'entrée (f@g)@x ? Cela équivaut à f[g][x] . Et si f et g étaient des fonctions ordinaires en mathématiques, ce serait inutile, mais si f est une fonction d'ordre supérieur , alors f[g] lui-même peut être une fonction qui peut très bien être appliquée à x .

Notez ici qu'il y a encore une certaine complexité. Dans f[] - f est fonction d'un argument. Et f[] équivaut à écrire Function[a, f[a]][x] . Mais qu'en est-il de la fonction de deux arguments, disons, f[x,y] ? Cela peut être écrit comme la Function[{a,b},f[a, b]][x, y] . Mais qu'en est-il de la Function[{a},f[a,b]] ? Qu'est ce que c'est Il existe une "variable libre" b , qui est simplement passée à la fonction. Function[{b},Function[{a},f[a,b]]] liera cette variable, puis la Function[{b},Function[{a},f [a, b]]][y][x] donne à nouveau f[x,y] . (Définir la fonction de sorte qu'elle ait un argument s'appelle "currying" en l'honneur du scientifique logicien nommé Haskell Curry ).

S'il existe des variables libres, c'est-à-dire qu'il existe de nombreuses difficultés différentes quant à la façon dont les fonctions peuvent être définies, mais si nous nous limitons aux objets Function ou λ qui n'ont pas de variables libres, alors elles peuvent fondamentalement être définies librement. Ces objets sont appelés combinateurs.

Les combinateurs ont une longue histoire. On sait qu'ils ont été proposés pour la première fois en 1920 par le disciple de David Gilbert , Moses Schoenfinkel .

À cette époque, ce n'est que très récemment qu'il a été découvert que vous n'aviez pas besoin d'utiliser les expressions And , Or et Not pour représenter les expressions dans la logique propositionnelle standard: il suffisait d'utiliser le seul opérateur, que nous appellerons maintenant Nand (parce que, par exemple, si nous écrivons Nand comme ·, Alors Or[a,b] prend la forme (a · a) · (b · b) ). Schönfinkel voulait trouver la même représentation minimale de la logique des prédicats, ou essentiellement de la logique, y compris les fonctions.

Il est venu avec deux «combinateurs» S et K. Dans la langue Wolfram, cela est écrit comme
K [x _] [y_] → x et S [x _] [y _] [z_] → x [z] [y [z]].

Il est à noter qu'il était possible d'utiliser ces deux combinateurs pour effectuer des calculs. Donc par exemple

S [K [S]] [S [K [S [K [S]]]] [S [K [K]]]]

peut être utilisé comme une fonction pour ajouter deux entiers.

Tous ces éléments, pour le dire en douceur, sont des objets plutôt abstraits, mais maintenant que nous comprenons ce que sont les machines de Turing et le calcul lambda, nous pouvons voir que les combinateurs de Schoenfinkel ont réellement anticipé le concept de l'informatique universelle. (Et encore plus remarquable, les définitions de S et K de 1920 sont minimalement simples, et ressemblent à la machine de Turing universelle très simple que j'ai proposée dans les années 1990, dont l'universalité a été prouvée en 2007 ).

Mais revenons à notre brochure et à notre ligne PI1IIx . Les caractères enregistrés ici sont des combinateurs, et ils sont tous conçus pour définir une fonction. Ici, la définition est que la superposition des fonctions doit être associative à gauche, donc fgx ne doit pas être interprété comme f @ g @ x ou f @ (g @ x) ou f [g [x]], mais plutôt comme (f @ g ) @x ou f [g] [x]. Nous allons traduire cette entrée dans un format pratique pour être utilisé par Wolfram Language: PI1IIx prendra la forme p [i] [one] [i] [i] [x] .

Pourquoi écrire quelque chose comme ça? Afin d'expliquer cela, nous devons discuter du concept de numéros d'église (nommé d'après l'église d'Alonzo). Disons que nous travaillons simplement avec des symboles et avec des lambdas ou des combinateurs. Existe-t-il un moyen de les utiliser pour spécifier des entiers?

Que diriez-vous simplement de dire que le nombre n correspond à la Function[x, Nest[f,x,n]] ? Ou, en d'autres termes, que (en notation plus courte):

1 est f[#]&
2 est f[f[#]]&
3 est f[f[f[#]]]& et ainsi de suite.

Tout cela peut sembler un peu plus obscur, mais la raison pour laquelle il est intéressant, c'est qu'il nous permet de tout faire complètement symbolique et abstrait, sans avoir à parler explicitement de quelque chose comme des entiers.

Avec cette méthode de spécification des nombres, imaginez, par exemple, ajouter deux nombres: 3 peut être représenté par f[f[f[#]]]& et 2 est f[f[#]]& . Vous pouvez les ajouter simplement en appliquant l'un d'eux à l'autre:



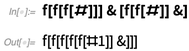
Mais à quoi ressemble f ? Ça pourrait être n'importe quoi! Dans un sens, "aller à lambda" à la fin et représenter des nombres en utilisant des fonctions qui prennent f comme argument. En d'autres termes, imaginez 3, par exemple, comme Function[f,f[f[f[#]]] &] ou Function[f,Function[x,f[f[f[x]]]] . (quand et comment vous devez nommer les variables est un problème dans le calcul lambda).

Considérons un fragment de l'article de Turing de 1937, Computability and λ-Diffusibility , qui définit les objets exactement comme nous venons de le dire:



Ici, l'enregistrement peut être quelque peu déroutant. Le x de Turing est notre f , et son x ' (le compositeur a fait une erreur en insérant un espace) est notre x . Mais ici, la même approche est utilisée.

Examinons donc la ligne immédiatement après le pli devant la feuille. C'est I1IIYI1IIx . Selon la forme du Wolfram Language, ce sera i[one][i][i][y][i][one][i][i][x] . Mais ici, i est une fonction identique, donc i[one] n'en renvoie qu'une seule . Pendant ce temps, l' un est la représentation numérique de Church pour 1 ou Function[f,f[#]&] . Mais avec cette définition, one[] devient a[#]& et one[a][b] devient a[b] . (Soit dit en passant, i[][b] , ou l' Identity[][b] également un [b] ).

Ce sera beaucoup plus clair si nous écrivons les règles de remplacement pour i et one , au lieu d'utiliser directement le calcul lambda. Le résultat sera le même. Appliquez ces règles de manière explicite, nous obtenons:



Et c'est exactement la même chose que celle présentée sur le premier enregistrement abrégé:



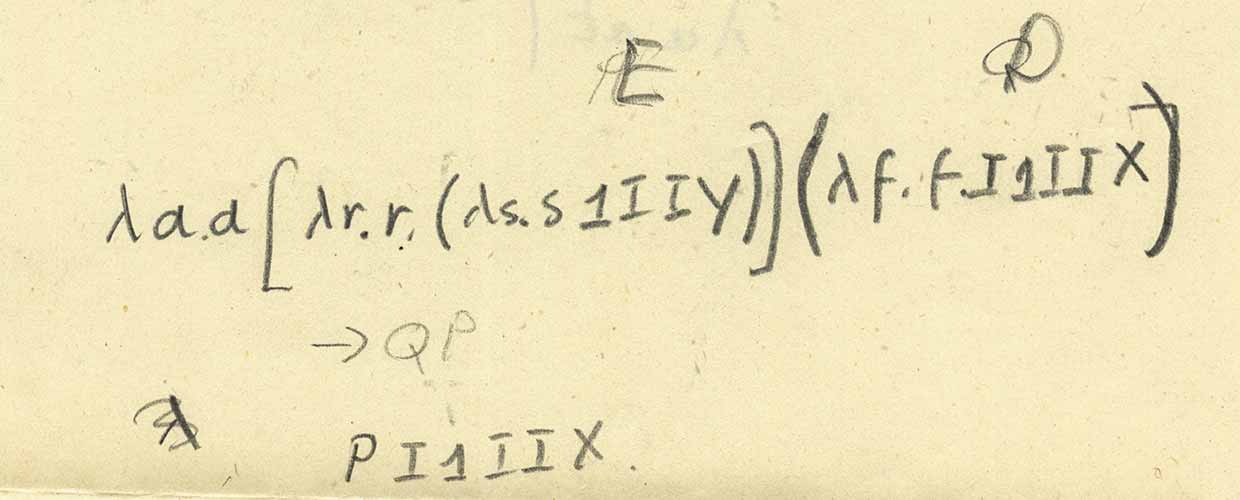
Regardons à nouveau la feuille, en haut:



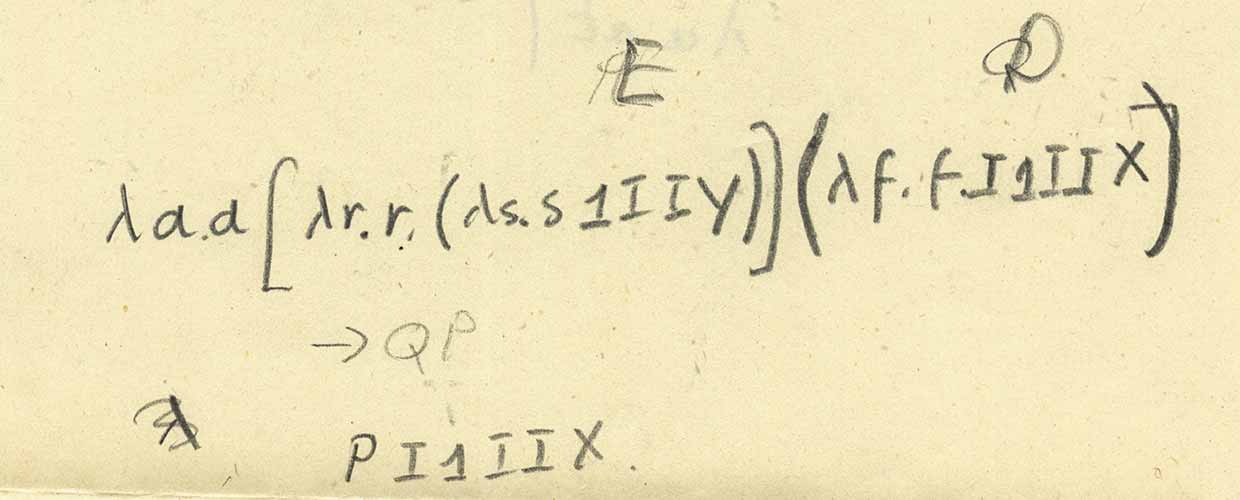
Ici, il y a des objets plutôt confus et incompréhensibles "E" et "D", mais par eux nous entendons "P" et "Q", donc nous pouvons écrire l'expression et la calculer (notez qu'ici - après une certaine confusion avec le tout dernier) symbole - "mystérieux scientifique" met [...] et (...) pour représenter les fonctions de l'application):



C'est donc la première abréviation montrée. Pour en voir plus, substituons les définitions de Q:



Nous obtenons exactement l'abréviation suivante montrée. Que se passe-t-il si nous substituons les expressions à P?



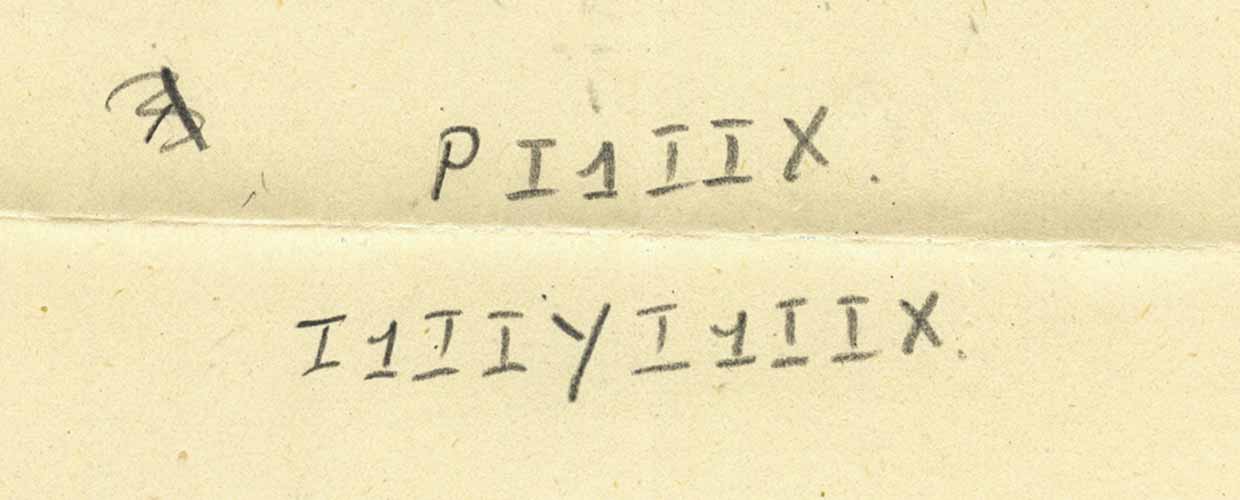
Voici le résultat:



Et maintenant, en utilisant le fait que i est une fonction qui génère l'argument lui-même, nous obtenons:



Oops! Mais ce n'est pas la prochaine ligne enregistrée. Y a-t-il une erreur ici? Ce n'est pas clair. Parce qu'au final, contrairement à la plupart des autres cas, il n'y a pas de flèche indiquant que la ligne suivante découle de la précédente.

Voici une sorte de mystère, mais passons au bas de la brochure:



Ici 2 est le numéro de l'Église, défini, par exemple, par le modèle two[a_] [b_] → a[a[b]] . Notez que c'est en fait la forme de la deuxième ligne si a est traité comme Function[r,r[]] et b comme q . Nous nous attendons donc à ce que le résultat des calculs soit le suivant:



Néanmoins, l'expression [b] située à l'intérieur peut être écrite comme x (diffère probablement de x précédemment écrite sur la feuille) - en conséquence, nous obtenons le résultat final:



Donc, nous pouvons déchiffrer un peu ce qui se passe sur cette feuille, mais au moins une énigme qui reste est ce que Y devrait être.

En fait, la logique combinatoire a un combinateur Y standard: le soi-disant combinateur à virgule fixe . Formellement, il est défini par le fait que Y [ f ] doit être égal à f [Y [ f ]], ou, en d'autres termes, Y [ f ] ne change pas lorsque f est appliqué, c'est donc un point fixe pour f . (Le combinateur Y est associé au numéro 0 dans le langage Wolfram.)

Actuellement, le Y-combinator est devenu célèbre grâce à l' accélérateur de lancement Y-Combinator , dit Paul Graham (qui pendant longtemps était un fan de la programmation fonctionnelle et du langage de programmation LISP et a implémenté la toute première boutique en ligne basée sur ce langage). Il m'a dit une fois personnellement: " personne ne comprend ce que Y est un combinateur ". (Il est à noter que Y Combinator est exactement ce qui permet aux entreprises d'éviter les opérations en virgule fixe ...)

Le combinateur Y (comme un combinateur à virgule fixe) a été inventé plusieurs fois. Turing a vraiment trouvé sa mise en œuvre en 1937, qu'il a appelé Θ. Mais la lettre «Y» sur notre page est-elle un célèbre combinateur à virgule fixe? Peut-être pas. Alors, quel est notre «Y»? Considérez cette réduction:



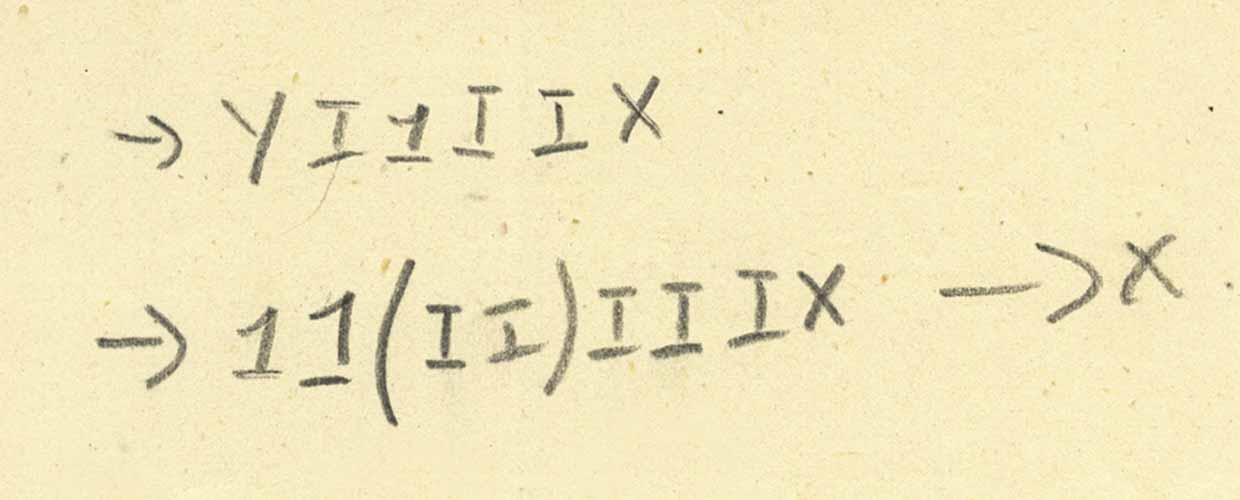
Mais cette information n'est clairement pas suffisante pour déterminer sans ambiguïté ce qu'est Y. Il est clair que Y fonctionne non seulement avec un seul argument; il semble qu'il s'agisse d'au moins deux arguments, mais on ne sait pas (du moins pour moi) combien d'arguments il faut pour entrer et ce qu'il fait.

Enfin, bien que nous puissions donner un sens à de nombreuses parties de la brochure, nous devons dire qu'à l'échelle mondiale, ce qui a été fait n'est pas clair. Même si cela nécessite beaucoup d'explications sur ce qui est présenté sur la feuille, il est assez élémentaire dans le calcul lambda et l'utilisation de combinateurs.

Vraisemblablement, voici une tentative de créer un «programme» simple - en utilisant le calcul lambda et les combinateurs pour faire quelque chose. Mais dans la mesure où cela est typique de la rétro-ingénierie, il nous est difficile de dire ce que devrait être ce «quelque chose» et ce qu'est un objectif «explicable» commun.

Il y a une autre caractéristique présentée sur la feuille, qui mérite d'être commentée ici - est l'utilisation de différents types de supports. En mathématiques traditionnelles, les parenthèses sont principalement utilisées pour tout - et les applications d'une fonction (comme dans f (x) ), et les regroupements de membres (comme dans (1 + x) (1-x) , ou, moins évidemment, a (1- x) ). (Dans Wolfram Language, nous séparons les différentes utilisations des crochets - entre crochets pour définir les fonctions f [x] - et les parenthèses ne sont utilisées que pour le regroupement).

Lorsque le calcul lambda est apparu pour la première fois, il y avait beaucoup de questions sur l'utilisation des parenthèses. Plus tard, Alan Turing a écrit un ouvrage entier (non publié) intitulé « Transformer la forme mathématique de la notation et de la phraséologie », mais déjà en 1937, il a estimé qu'il devait décrire des définitions modernes (plutôt hacker) pour le calcul lambda (qui, soit dit en passant, est apparu à partir de pour l'Église).

Il a dit que f appliqué à g devrait être écrit {f} (g) , sauf si f est le seul caractère, auquel cas il pourrait être f (g) . Il a ensuite dit que lambda (comme dans la Function[a, b] ) devrait être écrit comme λ a [ b ] ou, alternativement, λ a . b .

Cependant, peut-être qu'en 1940, l'idée d'utiliser {...} et [...] pour désigner différents objets a été abandonnée, principalement en faveur des crochets dans un style mathématique standard.

Jetez un œil en haut de la page:



Sous cette forme, il est difficile à comprendre. Dans les définitions de l'Église, les crochets sont destinés au regroupement, avec un crochet d'ouverture qui remplace une période. En utilisant cette définition, il devient clair que Q (éventuellement étiqueté comme D), placé entre parenthèses à la fin, est ce à quoi s'applique tout le lambda initial.

En fait, le crochet carré ici ne limite pas le corps de la lambda; au lieu de cela, il représente en fait une autre application de la fonction, et il n'y a aucune indication explicite de la fin du corps lambda. En fin de compte, il est clair que le «scientifique mystérieux» a changé le crochet carré de fermeture en un crochet rond, appliquant ainsi efficacement la définition de Church - et l'obligeant ainsi à calculer l'expression, comme indiqué sur la feuille.

Alors qu'est-ce que ce petit morceau signifie de toute façon? Je pense que cela suggère que la page a été écrite dans les années 1930, ou pas trop longtemps après, car la légende des crochets n'était pas encore établie.

Alors, de qui était cette écriture?

Donc, avant cela, nous avons parlé de ce qui est écrit sur la page. Mais qu'en est-il de celui qui l'a tout de même écrit?

Le candidat le plus évident pour ce rôle serait Alan Turing lui-même, car, après tout, la page était à l'intérieur de son livre. En termes de contenu, il semble qu'il n'y ait rien d'incompatible avec le fait qu'Alan Turing puisse écrire ceci - même au moment où il a commencé à traiter le calcul lambda après avoir reçu l'article de Church au début de 1936.

Et l'écriture manuscrite? Appartient-il à Alan Turing? Considérez plusieurs échantillons survivants, qui, comme nous le savons avec certitude, ont été écrits par Alan Turing:



Le texte présenté semble clairement très différent, mais qu'en est-il de la notation utilisée dans le texte? Au moins, à mon avis, cela ne semble pas si évident - et nous pouvons supposer que toute différence peut être causée par le fait que les échantillons existants (présentés dans les archives) sont écrits, pour ainsi dire, «à la fin», tandis que le nôtre une page est le reflet du travail de la pensée.

Il s'est avéré pratique pour notre enquête qu'il y avait une page dans les archives de Turing sur laquelle il a écrit un tableau de caractères nécessaires à la notation. Et en comparant ces caractères lettre par lettre, ils me ressemblent beaucoup (ces enregistrements ont été faits à l' époque de Turing, alors qu'il étudiait la croissance des plantes , d'où la mention «zone foliaire»):



Je voulais approfondir cette question, j'ai donc envoyé des échantillons à Sheila Lowe , une experte en écriture professionnelle (et auteur d'écriture manuscrite), que j'ai rencontrée une fois - présentant simplement notre brochure comme «échantillon A» et l'écriture manuscrite existante de Turing comme "Échantillon" B ". Sa réponse a été finale et négative: « Le style d'écriture est complètement différent. Quant à la personnalité, l'auteur de l'échantillon «B» a une façon de penser plus rapide et plus intuitive que l'auteur de l'échantillon «A ». »

Je n'étais pas encore complètement convaincu de cela, mais j'ai décidé qu'il était temps de chercher d'autres options.

Donc, s'il s'avère que Turing n'a pas écrit cela, alors qui l'a fait? Norman Rutledge m'a dit qu'il avait reçu le livre de Robin Gandhi, qui était l'exécuteur testamentaire de Turing. J'ai donc envoyé "Sample" C "" de Gandhi:



Mais la conclusion initiale de Sheila était que les trois échantillons ont probablement été écrits par trois personnes différentes, notant à nouveau que l'échantillon «B» a été obtenu du « penseur le plus rapide - celui qui est le plus susceptible de chercher le plus volontiers des solutions inhabituelles aux problèmes » . (Je trouve agréable qu'un spécialiste de l'écriture moderne donne une telle évaluation de l'écriture de Turing, étant donné à quel point tout le monde dans les travaux scolaires de Turing des années 1920 se plaignait de son écriture).

Eh bien, à ce moment-là, il semblait que Turing et Gandhi étaient exclus de la liste des «suspects». Alors, qui pourrait écrire ça? J'ai commencé à penser à des gens à qui Turing pouvait prêter son livre. Bien sûr, en même temps, ils devraient être capables de faire des calculs en utilisant le calcul lambda.

J'ai suggéré que la personne soit originaire de Cambridge, ou du moins d'Angleterre, étant donné le filigrane sur papier. J'ai fait l'hypothèse de travail selon laquelle 1936 environ était le bon moment pour écrire ceci. Alors, qui connaissait-il à ce moment-là et avec qui Turing communiquait-il? . ( 13 , 1930 1936 .)

. , , , — 1933 , («» ) : 0.12345678910111213… ( 1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, , «» , ).

1937 - , , . ( , - ).

, ( ) , . ( , 1948 Turbochamp — , , ).

? LinkedIn, , , Microsoft. , , . ( ):



, ( f . .)

? , . « », , . ( , , , , , ).

— , .

«»

, . , , , , , .

, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .

? - (, , , 2005 , «»). , « ».

- , , , ? . , - - - . , 1955 « » ( , BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .

. , , , « ». , , , , 1954 , . , , .

, « ( , ) » « , , , , [ ] ». , ? . ( , , , 1902 , « » : « »).

, , , , , 12 , -, , , 21 ).

, , - . , - . , , , 1938 . 2000 - ( ) — , , 2002 , .

, , ? , , . :



, . , , , , , .

: ? , , , .

- , — 1940 — . , 1944 , , . , , .

, , , , 1952 , « » . , , , , — , , . , . , , , , . , 1980- , “ » — , , , . ( , , , , « , »). , « , , , — … », , « ».)

, , . . , « » (. . -), -.

. 1969 , , , , , .
, , . . — — . . - , , .

1995 , . — . . , , — , , , . , , , , , 24 . ( 2001 — 45 ).

, ? , , , , , ( , , , c ). ( ) « » ( ), , -, , . , .

, . , 30 , . , , , - — , , , (, , , Mathematica ). , , , , , , , . , , , .

? , , () , . ( , .) , 1 . , .

, , . : « ! » , . . , -, , , .

, , , , , . , : . ; .

, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.

, - , , , . , , , , , , . , , — , , …

: ( ), ( ) ( ).

Wolfram Language?
.
Inscription aux nouveaux cours . Cours en ligne prêt.
Wolfram Language.