Résoudre l'équation de la régression linéaire simple

L'article présente plusieurs méthodes pour déterminer l'équation mathématique d'une droite de régression simple (par paire).

Toutes les méthodes de résolution de l'équation discutées ici sont basées sur la méthode des moindres carrés. Nous désignons les méthodes comme suit:

• Solution analytique
• Descente en pente
• Descente de gradient stochastique

Pour chacune des méthodes de résolution de l'équation de la ligne droite, l'article décrit diverses fonctions qui sont principalement divisées en celles qui sont écrites sans utiliser la bibliothèque NumPy et celles qui utilisent NumPy pour les calculs. On pense que l'utilisation habile de NumPy réduit les coûts informatiques.

Tout le code de cet article est écrit en python 2.7 à l'aide du bloc-notes Jupyter . Code source et exemple de fichier de données publiés sur github

L'article est plus axé sur les débutants et ceux qui ont déjà commencé à maîtriser l'étude d'une section très étendue en intelligence artificielle - l'apprentissage automatique.

Pour illustrer le matériel, nous utilisons un exemple très simple.

Exemples de conditions

Nous avons cinq valeurs qui caractérisent la dépendance de Y sur X (tableau n ° 1):

Tableau n ° 1 "Conditions de l'exemple"



Nous supposons que les valeurs $$$x_i$ Est le mois de l'année, et $$$y_i$ - revenus ce mois-ci. En d'autres termes, les revenus dépendent du mois de l'année, et $$$x_i$ - le seul signe dont dépendent les revenus.

Un exemple est moyen, à la fois en termes de dépendance conditionnelle des revenus sur le mois de l'année, et en termes de nombre de valeurs - ils sont très peu nombreux. Cependant, cette simplification permettra à ce qu'on appelle sur les doigts d'expliquer, pas toujours avec facilité, la matière absorbée par les débutants. Et aussi la simplicité des chiffres permettra, sans coûts de main d'œuvre importants, à ceux qui souhaitent résoudre l'exemple sur papier.

Supposons que la dépendance montrée dans l'exemple puisse être assez bien approximée par l'équation mathématique d'une droite de régression simple (par paire) de la forme:

$$

$$Y = a + bx$$

où $$$x$ - c'est le mois au cours duquel les recettes ont été perçues, $$$Y$ - revenus correspondant au mois, $$$a$ et $$$b$ - coefficients de régression de la droite estimée.

Notez que le coefficient $$$b$ souvent appelée pente ou gradient de la ligne estimée; représente le montant à modifier $$$Y$ lors du changement $$$x$ .

De toute évidence, notre tâche dans l'exemple est de sélectionner ces coefficients dans l'équation $$$a$ et $$$b$ pour lesquels les écarts de nos revenus mensuels estimés par rapport aux vraies réponses, à savoir les valeurs présentées dans l'échantillon seront minimales.

Méthode des moindres carrés

Conformément à la méthode des moindres carrés, l'écart doit être calculé en le mettant au carré. Une telle technique évite le remboursement mutuel des écarts, s'ils ont des signes opposés. Par exemple, si dans un cas, l'écart est +5 (plus cinq) et dans l'autre -5 (moins cinq), alors la somme des écarts sera mutuellement remboursée et sera 0 (zéro). Vous ne pouvez pas gaspiller l'écart, mais utilisez la propriété du module et tous les écarts seront positifs et s'accumuleront en nous. Nous ne nous attarderons pas sur ce point en détail, mais indiquons simplement que pour la commodité des calculs, il est habituel de quadriller l'écart.

Voici à quoi ressemble la formule à l'aide de laquelle nous déterminons la plus petite somme des écarts au carré (erreurs):

$$

$$ERR (x) = \ sum \ limits_ {i = 1} ^ n (a + bx_i - y_i) ^ 2 = \ sum \ limits_ {i = 1} ^ n (f (x_i) -y_i) ^ 2 \ rightarrow min$$

où $$$f (x_i) = a + bx_i$ Est une fonction d'approximation des vraies réponses (c'est-à-dire des revenus que nous avons calculés),

$$$y_i$ - ce sont de vraies réponses (revenus fournis dans l'échantillon),

$$$i$ Est l'indice d'échantillon (le numéro du mois au cours duquel l'écart est déterminé)

Nous différencions la fonction, définissons les équations aux dérivées partielles et sommes prêts à passer à la solution analytique. Mais d'abord, prenons une courte digression sur ce qu'est la différenciation et rappelons la signification géométrique de la dérivée.

Différenciation

La différenciation est l'opération de recherche de la dérivée d'une fonction.

À quoi sert un dérivé? La dérivée d'une fonction caractérise le taux de changement d'une fonction et indique sa direction. Si la dérivée à un point donné est positive, alors la fonction augmente, sinon la fonction diminue. Et plus la valeur de la dérivée modulo est grande, plus le taux de variation des valeurs de la fonction est élevé, plus l'angle du graphique de la fonction est raide.

Par exemple, dans les conditions d'un système de coordonnées cartésiennes, la valeur de la dérivée au point M (0,0) égale à +25 signifie qu'à un point donné, lorsque la valeur est décalée $$$x$ droit à l'unité arbitraire, valeur $$$y$ augmente de 25 unités conventionnelles. Sur le graphique, cela ressemble à un angle d'élévation assez raide $$$y$ à partir d'un point donné.

Un autre exemple. Une valeur dérivée de -0,1 signifie qu'en cas de décalage $$$x$ par unité conventionnelle, valeur $$$y$ diminue de seulement 0,1 unité conventionnelle. Dans le même temps, sur le graphique de fonction, nous pouvons observer une inclinaison à peine perceptible vers le bas. En dessinant une analogie avec la montagne, nous semblons descendre très lentement la pente douce de la montagne, contrairement à l'exemple précédent, où nous devions prendre des pics très raides :)

Ainsi, après avoir différencié la fonction $$$ERR (x) = \ sum \ limits_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ par coefficients $$$a$ et $$$b$ , nous définissons les équations des dérivées partielles du premier ordre. Après avoir défini les équations, nous obtenons un système de deux équations, décidant que nous pouvons choisir ces valeurs des coefficients $$$a$ et $$$b$ où les valeurs des dérivées correspondantes à des points donnés changent d'une valeur très, très petite, et dans le cas de la solution analytique, elles ne changent pas du tout. En d'autres termes, la fonction d'erreur aux coefficients trouvés atteint un minimum, car les valeurs des dérivées partielles à ces points seront nulles.

Donc, selon les règles de différenciation, l'équation de la dérivée partielle du 1er ordre par rapport au coefficient $$$a$ prendra la forme:

$$

Équation dérivée partielle de premier ordre par rapport à $$$b$ prendra la forme:

$$

En conséquence, nous avons obtenu un système d'équations qui a une solution analytique assez simple:

\ commencer {équation *}
\ begin {cases}
na + b \ somme \ limites_ {i = 1} ^ nx_i - \ somme \ limites_ {i = 1} ^ ny_i = 0
\\
\ sum \ limits_ {i = 1} ^ nx_i (a + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i) = 0
\ end {cases}
\ end {équation *}

Avant de résoudre l'équation, préchargez, vérifiez le chargement correct et formatez les données.

Télécharger et formater les données

Il convient de noter qu'en raison du fait que pour la solution analytique, et plus tard pour la descente de gradient et de gradient stochastique, nous utiliserons le code en deux variantes: en utilisant la bibliothèque NumPy et sans l'utiliser, nous devrons formater les données en conséquence (voir code).

Visualisation

Maintenant, après avoir, premièrement, téléchargé les données, deuxièmement, nous avons vérifié le chargement correct et enfin formaté les données, nous allons effectuer la première visualisation. Souvent, la méthode pairplot de la bibliothèque Seaborn est utilisée pour cela. Dans notre exemple, en raison du nombre limité, cela n'a aucun sens d'utiliser la bibliothèque Seaborn . Nous utiliserons la bibliothèque Matplotlib régulière et ne regarderons que le nuage de points.


Annexe n ° 1 «Dépendance des revenus par rapport au mois de l'année»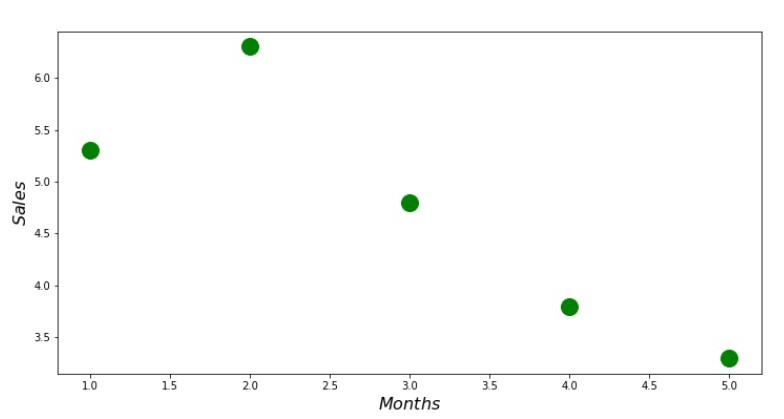

Solution analytique

Nous allons utiliser les outils les plus courants en python et résoudre le système d'équations:

\ commencer {équation *}
\ begin {cases}
na + b \ somme \ limites_ {i = 1} ^ nx_i - \ somme \ limites_ {i = 1} ^ ny_i = 0
\\
\ sum \ limits_ {i = 1} ^ nx_i (a + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i) = 0
\ end {cases}
\ end {équation *}

Selon la règle de Cramer, nous trouvons un déterminant commun, ainsi que des déterminants par $$$a$ et par $$$b$ , après quoi, en divisant le déterminant par $$$a$ sur le déterminant commun - on trouve le coefficient $$$a$ , de même, trouver le coefficient $$$b$ .


Voici ce que nous avons obtenu:



Ainsi, les valeurs des coefficients sont trouvées, la somme des écarts au carré est définie. On trace une droite sur l'histogramme de diffusion en fonction des coefficients trouvés.


Annexe n ° 2 «Réponses correctes et estimées»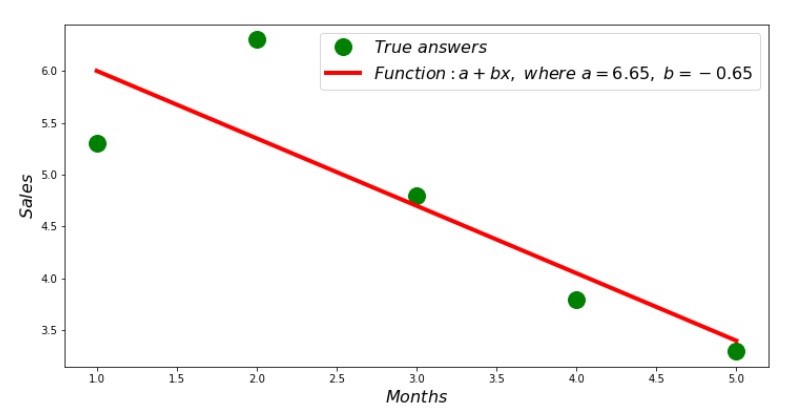



Vous pouvez consulter le calendrier des écarts pour chaque mois. Dans notre cas, nous ne pouvons en retirer aucune valeur pratique significative, mais nous satisferons la curiosité de savoir dans quelle mesure l'équation de régression linéaire simple caractérise la dépendance des revenus par rapport au mois de l'année.


Annexe n ° 3 «Écarts,%»



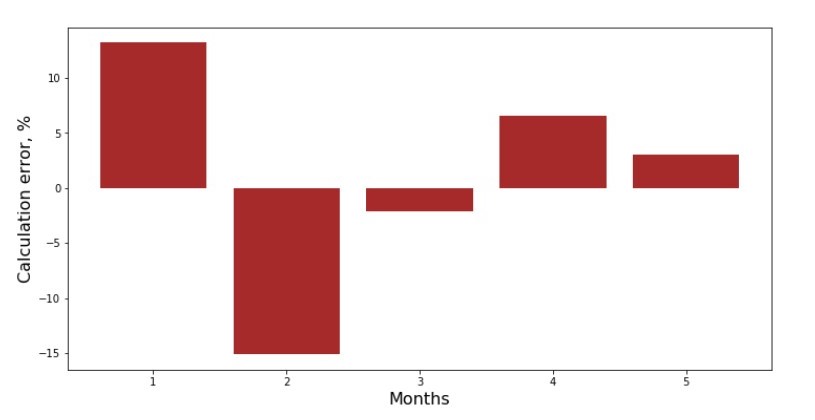
Pas parfait, mais nous avons terminé notre tâche.

Nous écrivons une fonction qui, pour déterminer les coefficients $$$a$ et $$$b$ utilise la bibliothèque NumPy , plus précisément, nous écrirons deux fonctions: l'une utilisant une matrice pseudo-inverse (non recommandée dans la pratique, car le processus est complexe sur le plan informatique et instable), l'autre utilisant une équation matricielle.


Comparez le temps nécessaire pour déterminer les coefficients $$$a$ et $$$b$ , selon les 3 méthodes présentées.




Sur une petite quantité de données, une fonction «auto-écrite» apparaît qui trouve les coefficients en utilisant la méthode Cramer.

Vous pouvez maintenant passer à d'autres façons de trouver les coefficients $$$a$ et $$$b$ .

Descente en pente

Définissons d'abord ce qu'est un dégradé. D'une manière simple, un gradient est un segment qui indique la direction de la croissance maximale d'une fonction. Par analogie avec une montée, où le gradient semble, il y a la montée la plus raide jusqu'au sommet de la montagne. En développant l'exemple de la montagne, nous rappelons qu'en fait, nous avons besoin de la descente la plus raide pour atteindre la plaine le plus tôt possible, c'est-à-dire le minimum - l'endroit où la fonction n'augmente ni ne diminue. À ce stade, la dérivée sera nulle. Par conséquent, nous n'avons pas besoin d'un gradient, mais d'un anti-gradient. Pour trouver l'anti-gradient, il vous suffit de multiplier le gradient par -1 (moins un).

Nous attirons l'attention sur le fait qu'une fonction peut avoir plusieurs minima, et étant descendue dans l'un d'entre eux selon l'algorithme proposé ci-dessous, nous ne pourrons pas trouver un autre minimum éventuellement inférieur à celui trouvé. Détendez-vous, nous ne sommes pas en danger! Dans notre cas, nous avons affaire à un minimum unique, puisque notre fonction $$$\ sum \ limits_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ sur le graphique est une parabole ordinaire. Et comme nous le savons tous très bien du cursus scolaire de mathématiques, la parabole n'a qu'un minimum.

Après avoir compris pourquoi nous avions besoin d'un gradient, et aussi que le gradient est un segment, c'est-à-dire un vecteur avec des coordonnées données, qui sont exactement les mêmes coefficients $$$a$ et $$$b$ nous pouvons implémenter la descente de gradient.

Avant de commencer, je suggère de lire quelques phrases sur l'algorithme de descente:

• Nous déterminons les coordonnées des coefficients de manière pseudo-aléatoire $$$a$ et $$$b$ . Dans notre exemple, nous déterminerons les coefficients proches de zéro. Il s'agit d'une pratique courante, mais chaque pratique peut avoir sa propre pratique.
• De coordonnée $$$a$ soustraire la valeur de la dérivée partielle du 1er ordre au point $$$a$ . Donc, si la dérivée est positive, la fonction augmente. Par conséquent, en enlevant la valeur du dérivé, nous nous déplacerons dans le sens opposé de la croissance, c'est-à-dire dans le sens de la descente. Si la dérivée est négative, alors la fonction à ce point diminue et en enlevant la valeur de la dérivée, nous nous dirigeons vers la descente.
• Nous effectuons une opération similaire avec les coordonnées $$$b$ : soustraire la valeur de la dérivée partielle au point $$$b$ .
• Afin de ne pas sauter le minimum et de ne pas voler dans l'espace lointain, il est nécessaire de régler la taille du pas vers la descente. En général, vous pouvez écrire un article entier sur la façon de définir correctement l'étape et comment la modifier pendant la descente pour réduire le coût des calculs. Mais maintenant, nous avons une tâche légèrement différente, et nous allons établir la taille du pas par la méthode scientifique de «piquer» ou, comme on dit chez les gens du commun, empiriquement.
• Après que nous soyons à partir des coordonnées données $$$a$ et $$$b$ soustrait les valeurs des dérivées, on obtient de nouvelles coordonnées $$$a$ et $$$b$ . Nous passons à l'étape suivante (soustraction), déjà à partir des coordonnées calculées. Et donc le cycle recommence encore et encore, jusqu'à ce que la convergence requise soit atteinte.

C'est tout! Nous sommes maintenant prêts à partir à la recherche des gorges les plus profondes de la fosse des Mariannes. Descendre.




Nous avons plongé tout en bas de la fosse des Mariannes et là nous avons trouvé toutes les mêmes valeurs des coefficients $$$a$ et $$$b$ , ce qui était en fait à prévoir.

Faisons une autre plongée, mais cette fois, le remplissage de notre véhicule hauturier sera d'autres technologies, à savoir la bibliothèque NumPy .



Valeurs de coefficient $$$a$ et $$$b$ immuable.

Voyons comment l'erreur a changé pendant la descente du gradient, c'est-à-dire comment la somme des écarts au carré a changé à chaque étape.


Graphique №4 «La somme des carrés des écarts dans la descente du gradient»



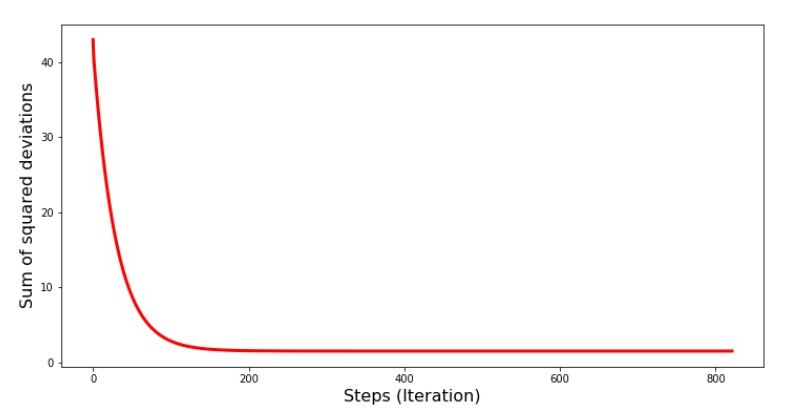
Sur le graphique, nous voyons qu'à chaque étape l'erreur diminue, et après un certain nombre d'itérations nous observons une ligne pratiquement horizontale.

Enfin, nous estimons la différence dans le temps d'exécution du code:




Peut-être que nous faisons quelque chose de mal, mais encore une fois, une simple fonction "auto-écrite" qui n'utilise pas la bibliothèque NumPy est en avance sur l'utilisation de la fonction utilisant la bibliothèque NumPy .

Mais nous ne restons pas immobiles, mais nous nous dirigeons vers l'étude d'une autre façon passionnante de résoudre l'équation de la régression linéaire simple. Rencontrez-moi!

Descente de gradient stochastique

Afin de comprendre rapidement le principe de fonctionnement de la descente en gradient stochastique, il est préférable de déterminer ses différences par rapport à la descente en gradient ordinaire. Nous, dans le cas de la descente de gradient, dans les équations des dérivées de $$$a$ et $$$a$ utilisé les sommes des valeurs de tous les attributs et les vraies réponses disponibles dans l'échantillon (c'est-à-dire les sommes de tous $$$x_i$ et $$$y_i$ ) En descente de gradient stochastique, nous n'utiliserons pas toutes les valeurs disponibles dans l'échantillon, mais à la place, de manière pseudo-aléatoire, nous choisirons ce que l'on appelle l'indice d'échantillon et utiliserons ses valeurs.

Par exemple, si l'indice est déterminé par le nombre 3 (trois), alors nous prenons les valeurs $$$x_3 = 3$ et $$$y_3 = 4,8$ , puis nous substituons les valeurs dans les équations des dérivées et déterminons les nouvelles coordonnées. Ensuite, après avoir déterminé les coordonnées, nous déterminons à nouveau pseudo-aléatoirement l'indice de l'échantillon, substituons les valeurs correspondant à l'indice dans les équations aux dérivées partielles et déterminons les coordonnées $$$a$ et $$$a$ etc. avant d' écologiser la convergence. À première vue, cela peut sembler fonctionner, mais cela fonctionne. Certes, il convient de noter que pas à chaque étape, l'erreur diminue, mais la tendance existe certainement.

Quels sont les avantages de la descente de gradient stochastique par rapport à l'habituel? Si notre taille d'échantillon est très grande et mesurée en dizaines de milliers de valeurs, alors il est beaucoup plus facile à traiter, disons un millier aléatoire d'entre elles que l'échantillon entier. Dans ce cas, la descente de gradient stochastique est lancée. Dans notre cas, bien sûr, nous ne remarquerons pas de grande différence.

Nous regardons le code.




Nous examinons attentivement les coefficients et nous nous posons la question «Comment cela?». Nous avons obtenu d'autres valeurs des coefficients $$$a$ et $$$b$ . Peut-être que la descente du gradient stochastique a trouvé des paramètres plus optimaux de l'équation? Hélas, non. Il suffit de regarder la somme des écarts au carré et de voir qu'avec les nouvelles valeurs des coefficients, l'erreur est plus grande. Ne vous précipitez pas au désespoir. Nous traçons le changement d'erreur.


Graphique №5 «La somme des carrés des écarts dans la descente du gradient stochastique»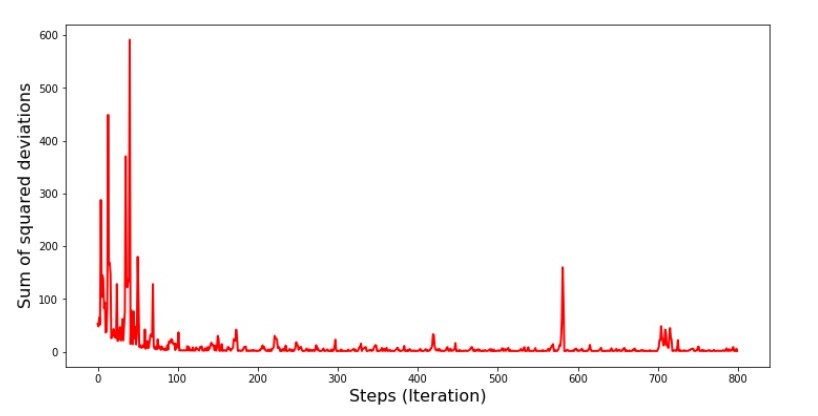



Après avoir regardé le calendrier, tout se met en place et maintenant nous allons tout réparer.

Que s'est-il donc passé? Les événements suivants se sont produits.Lorsque nous sélectionnons un mois au hasard, c'est pour le mois sélectionné que notre algorithme cherche à réduire l'erreur de calcul des revenus. Ensuite, nous sélectionnons un autre mois et répétons le calcul, mais nous réduisons déjà l'erreur pour le deuxième mois sélectionné. Et maintenant, rappelons que pendant les deux premiers mois, nous nous sommes considérablement écartés de la ligne de l'équation de la régression linéaire simple. Cela signifie que lorsque l'un de ces deux mois est sélectionné, puis en réduisant l'erreur de chacun d'eux, notre algorithme augmente sérieusement l'erreur dans tout l'échantillon. Alors que faire? La réponse est simple: vous devez réduire le pas de descente. Après tout, en diminuant le pas de descente, l'erreur cessera également de «sauter» de haut en bas. Au contraire, l'erreur "sauter" ne s'arrêtera pas, mais elle ne le fera pas aussi rapidement :) Nous allons vérifier.




Graphique n ° 6 «La somme des carrés des écarts dans la descente du gradient stochastique (80 000 pas)»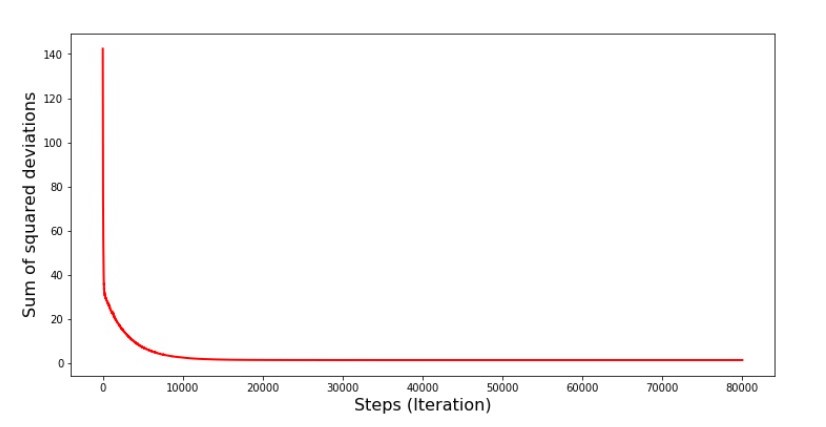



Les valeurs des coefficients se sont améliorées, mais ne sont toujours pas idéales. Hypothétiquement, cela peut être corrigé de cette façon. Par exemple, aux 1000 dernières itérations, nous choisissons les valeurs des coefficients avec lesquels l'erreur minimale a été commise. Certes, pour cela, nous devrons noter les valeurs des coefficients eux-mêmes. Nous ne le ferons pas, mais faisons plutôt attention au calendrier. Il semble lisse et l'erreur semble diminuer uniformément. Ce n'est en fait pas le cas. Regardons les 1000 premières itérations et comparons-les avec les dernières.


Annexe n ° 7 "La somme des carrés des écarts du SGD (1000 premiers pas)"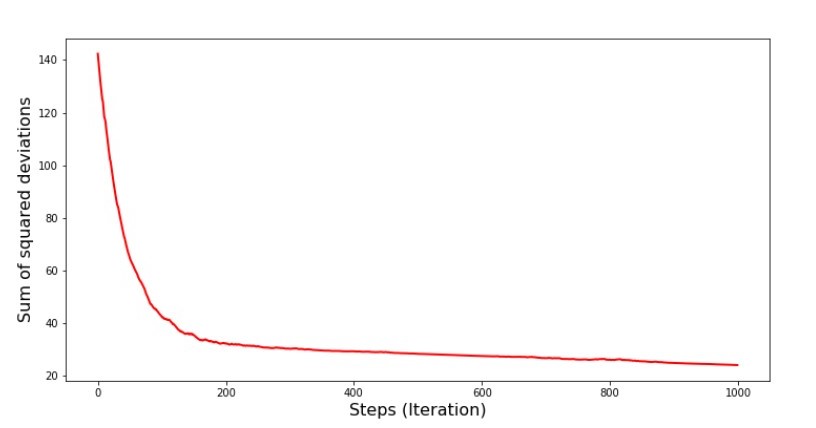



Graphique n ° 8 "La somme des carrés des écarts du SGD (1000 derniers pas)"



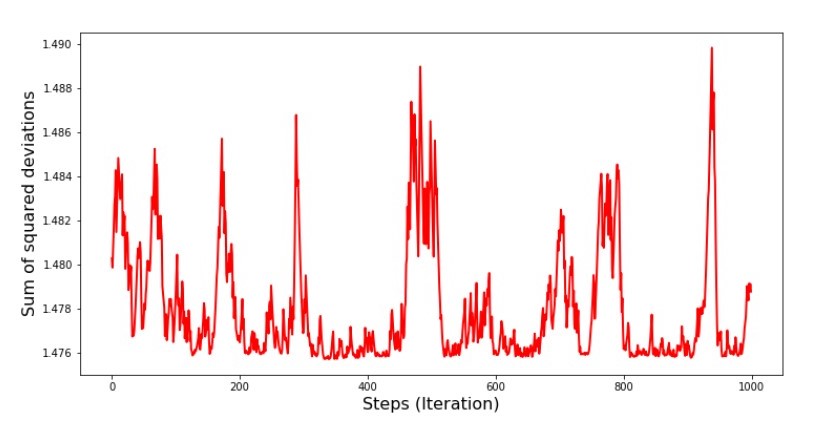Au tout début de la descente, on observe une diminution assez uniforme et forte des erreurs. Aux dernières itérations, nous voyons que l'erreur tourne autour et autour de la valeur de 1,475 et à certains points est même égale à cette valeur optimale, mais ensuite elle monte quand même ... Je répète, nous pouvons écrire les valeurs de$$$a$ et $$b , puis sélectionnez ceux pour lesquels l'erreur est minimale. Cependant, nous avons eu un problème plus grave: nous avons dû faire 80 000 pas (voir code) pour obtenir des valeurs proches de l'optimale. Et cela contredit déjà l'idée de gagner du temps de calcul avec une descente de gradient stochastique par rapport au gradient. Qu'est-ce qui peut être corrigé et amélioré? Il n'est pas difficile de remarquer que lors des premières itérations, nous descendons en toute confiance et, par conséquent, nous devons laisser un grand pas dans les premières itérations et réduire le pas à mesure que nous avançons. Nous ne le ferons pas dans cet article - il a déjà traîné. Ceux qui le souhaitent peuvent eux-mêmes réfléchir à la façon de procéder, ce n'est pas difficile :)Maintenant, nous allons effectuer une descente de gradient stochastique en utilisant la bibliothèqueNumPy$b$

(et nous ne tomberons pas sur les pierres que nous avons identifiées plus tôt)




Les valeurs se sont avérées être presque les mêmes que pendant la descente sans utiliser NumPy . Mais c'est logique.

Nous découvrirons combien de temps les descentes de gradient stochastique nous ont pris.




Plus la forêt est éloignée, plus les nuages ​​sont sombres: encore une fois, la formule «auto-écrite» donne le meilleur résultat. Tout cela suggère qu'il devrait y avoir des façons encore plus subtiles d'utiliser la bibliothèque NumPy , ce qui accélère vraiment les opérations de calcul. Dans cet article, nous ne les découvrirons pas. Il y aura quelque chose à penser à votre guise :)

Résumer

Avant de résumer, je voudrais répondre à la question qui s'est probablement posée à notre cher lecteur. Pourquoi, en fait, un tel «tourment» avec les descentes, pourquoi devons-nous monter et descendre la montagne (principalement vers le bas) pour trouver la plaine précieuse, si nous avons un appareil si puissant et simple entre nos mains, sous la forme d'une solution analytique qui nous téléporte instantanément vers bon endroit?

La réponse à cette question se trouve en surface. Maintenant, nous avons examiné un exemple très simple dans lequel la vraie réponse$$y i dépend d'un attribut$y_i$$$$x_i$ .Dans la vie, ce n'est pas souvent vu, alors imaginez que nous avons des signes de 2, 30, 50 ou plus. Ajoutez à cela des milliers, voire des dizaines de milliers de valeurs pour chaque attribut. Dans ce cas, la solution analytique peut ne pas réussir le test et échouer. À son tour, la descente de gradient et ses variations nous rapprocheront lentement mais sûrement de l'objectif - le minimum de la fonction. Et ne vous inquiétez pas de la vitesse - nous analyserons probablement aussi les méthodes qui nous permettront de définir et d'ajuster la longueur de pas (c'est-à-dire la vitesse).

Et maintenant, en fait, un bref résumé.

Premièrement, j'espère que le matériel présenté dans l'article aidera les débutants à «sortir avec des scientifiques» pour comprendre comment résoudre les équations de la régression linéaire simple (et pas seulement).

Deuxièmement, nous avons examiné plusieurs façons de résoudre l'équation. Maintenant, selon la situation, nous pouvons choisir celui qui est le mieux adapté pour résoudre le problème.

Troisièmement, nous avons vu la puissance de paramètres supplémentaires, à savoir la longueur de pas de la descente en gradient. Ce paramètre ne peut être négligé. Comme indiqué ci-dessus, afin de réduire le coût des calculs, la longueur de l'étape doit être modifiée le long de la descente.

Quatrièmement, dans notre cas, les fonctions «auto-écrites» ont montré le meilleur résultat temporel des calculs. Ceci est probablement dû à l'utilisation non professionnelle des capacités de la bibliothèque NumPy. Quoi qu'il en soit, la conclusion est la suivante. D'une part, il vaut parfois la peine de remettre en question les opinions établies et, d'autre part, cela ne vaut pas toujours la peine de compliquer les choses - au contraire, parfois une manière plus simple de résoudre un problème est plus efficace. Et comme notre objectif était d'analyser trois approches pour résoudre l'équation de la régression linéaire simple, l'utilisation de fonctions «auto-écrites» nous a suffi.

← Travaux précédents de l'auteur - «Nous étudions l'énoncé du théorème central limite en utilisant la distribution exponentielle»$\leftarrow$
→ Le prochain travail de l'auteur - «Nous apportons l'équation de régression linéaire sous forme matricielle»$\rightarrow$

Littérature (ou quelque chose comme ça)

1. La régression linéaire

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. La méthode des moindres carrés

mathprofi.ru/metod_naimenshih_kvadratov.html~~V~~singular~~3rd

3. Le dérivé

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4. Gradient

mathprofi.ru /proizvodnaja_po_napravleniju_i_gradient.html

5. Descente en

pente

habr.com/en/post/471458

habr.com/en/post/307312 artemarakcheev.com//2017-12-31/linear_regression

6. Bibliothèque NumPy

docs.scipy.org/doc/ numpy-1.10.1 / référence / généré / numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2. html