Nous avons examiné la méthode de Monte Carlo , nous verrons aujourd'hui comment l'esprit de l'ordinateur joue en 2048 en utilisant le bon vieux minimax avec écrêtage alpha-bêta.

L'article a été écrit avec le soutien d'EDISON, une entreprise qui développe des applications mobiles et fournit des services de test de logiciels .
Solution espionnée par le stackoverflow de l'utilisateur
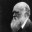 ovolve
ovolve , qui a noté dans la discussion
comment enseigner l'IA au jeu 2048 .
Traduction des commentaires de ovolveJe suis l'auteur du programme mentionné dans ce fil. Vous pouvez voir l'IA
en action ou voir
le code .
Actuellement, le programme gagne dans environ 90% des cas en exécutant des scripts java dans un navigateur sur mon ordinateur portable, dépensant 100 millisecondes pour réfléchir au cours, fonctionnant, bien que pas parfaitement, mais assez bien.
Comme le jeu est un espace d'état discret avec des informations complètes, étant en fait un jeu au tour par tour comme les échecs et les dames, j'ai utilisé les mêmes méthodes qui ont montré leurs performances dans ces jeux, à savoir la
recherche minimax avec
écrêtage alpha-bêta . Étant donné que les liens fournissent de nombreuses informations sur cet algorithme, je vais simplement parler des deux principales heuristiques que j'ai utilisées dans
la fonction d'estimation statique et formaliser de nombreuses hypothèses intuitives faites par d'autres personnes ici.

Monotonie
Cette heuristique tente de garantir que toutes les valeurs de tuiles augmentent ou diminuent à la fois à gauche / à droite et en haut / en bas. Cette heuristique à elle seule reflète la conjecture que beaucoup d'autres ont mentionné que des tuiles plus précieuses devraient être regroupées dans un coin. En règle générale, cela empêche l'accumulation de tuiles de moindre valeur et maintient le plateau organisé, car les petites tuiles se transforment en plus grandes.
Voici une capture d'écran d'une grille complètement monotone. J'ai eu cette situation en exécutant un algorithme avec la fonction eval installée afin d'ignorer les autres heuristiques et de ne prendre en compte que la monotonie.

Douceur (douceur, régularité)
L'heuristique ci-dessus en soi a tendance à créer des structures dans lesquelles les cellules voisines sont réduites en valeur, cependant, bien sûr, les voisins devraient avoir la même signification à combiner. Par conséquent, l'heuristique de lissage mesure simplement la différence de valeurs entre les tuiles adjacentes, en essayant de minimiser leur nombre.
Un commentateur de Hacker News a fourni une
formalisation intéressante de cette idée en termes de théorie des graphes.
Traduction de formalisation avec Hacker NewsHier, j'ai montré ce jeu à un collègue, un amoureux de la théorie des graphes, et nous avons également décidé de réfléchir à la façon de résoudre ce jeu en utilisant l'IA.
La solution la plus simple est minimax, qui, à mon avis, est assez bien implémentée. Si quelqu'un ici ne connaît pas minimax, OP a écrit un code très élégant et bien commenté qui serait un excellent tutoriel.
L'approche la moins intensive en calcul que nous avons proposée était de modéliser l'état du jeu sous la forme d'un graphique G (V, E) , où V est un ensemble de tuiles actives et E est un ensemble d'arêtes reliant des tuiles adjacentes pondérées par la fonction c (v1, v2) , qui renvoie la valeur absolue de la différence entre les deux tuiles. Pour chaque solution, l'IA choisit un coup qui minimise la somme des poids de tous les bords dans le nouvel état de jeu.
La raison en est que la seule façon de progresser dans le jeu est d'avoir des tuiles avec les mêmes valeurs côte à côte, pour lesquelles le poids en G sera 0. Ainsi, l'IA devrait essayer de minimiser le poids total. À la fin, il y aura un grand nombre sur les planches avec un grand poids de bords aux tuiles adjacentes, donc l'IA essaiera de garder ces tuiles à côté d'autres grandes tuiles pour minimiser la différence.
Étant donné que le jeu est stochastique, l'approche que j'ai décrite peut ne pas fonctionner dans le pire des cas, mais elle peut également être appliquée à la solution minimax existante en tant que fonction de pondération pour chaque nœud de l'arbre.
Voici une capture d'écran d'un maillage parfaitement lisse, gracieusement fourni par cette excellente
fausse fourche .
(lien vers l'archive Web, tandis que les scripts Java sur la page fonctionnent et que vous pouvez utiliser le clavier pour vous déplacer dans n'importe quelle direction - note du traducteur).Tuiles en vrac
Et enfin, il y a une pénalité pour avoir trop peu de tuiles gratuites, car les options peuvent rapidement se terminer lorsque le terrain de jeu devient trop étroit.
Et c'est tout! La recherche de l'espace de jeu tout en optimisant ces critères donne des performances étonnamment bonnes. L'un des avantages de l'utilisation d'une approche générique comme celle-ci plutôt que d'une stratégie de déplacement explicitement codée est que l'algorithme peut souvent trouver des solutions intéressantes et inattendues. Si vous observez sa progression, il fait souvent des mouvements étonnants mais efficaces, comme le changement soudain de murs ou de coins, près desquels il construit son jeu.

Petit changement
La capture d'écran montre la puissance de cette approche. J'ai supprimé la limite de tuiles (afin qu'elles continuent de croître après avoir atteint 2048), et voici le meilleur résultat après huit tests.
Oui, c'est 4096 avec 2048. =) Cela signifie qu'il a atteint la tuile 2048 insaisissable sur un plateau.
Le code Java-Script pour minimax avec écrêtage alpha-bêta et fonction d'évaluation statique de l'utilisateur ovover de stackoverflow est donné ci-dessous dans l'article.
La méthode minimax est consacrée à plusieurs excellents articles habr, donc nous omettons l'explication détaillée académique de ce qu'elle consiste. Pour ceux qui ont
rejoint la communauté informatique, j'ai récemment entendu les beaux termes «minimax» et «écrêtage alpha-bêta», mais je ne sais pas ce que cela signifie, essayons, littéralement en quelques paragraphes, d'expliquer la signification la plus générale.
Minimax
Dans certains jeux, le processus d'un jeu entre deux joueurs (qui se déplacent à leur tour) peut être représenté comme un soi-disant arbre d'options. Dans chaque position spécifique, chaque joueur a généralement le choix entre différentes options pour son mouvement. Et en réponse à chacune de ces options, un adversaire peut aussi ressembler à bien des égards.
Fragment d'un arbre d'optionsÉtant donné qu'à tout moment du jeu, il existe des informations complètes sur l'état du terrain de jeu, l'état actuel de la position peut toujours être estimé avec précision. Une telle fonction est appelée
fonction d'évaluation statique ou
SFO abrégé. De plus, plus cette fonction est importante lors de l'évaluation d'une position spécifique, plus la position est avantageuse pour un joueur (appelons-la le
joueur maximisant ). Plus la valeur numérique de cette fonction est petite lors de l'évaluation d'une position, plus la position du deuxième joueur est avantageuse (appelons-la le
joueur minimisant ).
Après chaque mouvement, la position change et donc son score change. Lors de l'examen de l'arbre des options, chaque joueur doit non seulement préférer les branches dans lesquelles le classement lui est le plus favorable. Vous devez également éviter les branches dans lesquelles l'évaluation de la position est favorable à l'adversaire.
On suppose que l'adversaire est également guidé par le rationalisme et évite également les options qui pourraient le conduire à perdre. Autrement dit, chaque joueur, lors du choix d'une option, procède de la maximisation de son propre avantage et en même temps de la minimisation du profit de l'adversaire.
C'est minimax.
Détourage alpha bêta
C'est assez évident: qui calcule un arbre d'une position donnée à une plus grande profondeur, il a plus de chances de gagner. Mais il y a une nuisance - l'arbre des options dans les jeux a la mauvaise habitude de se ramifier et de croître de façon exponentielle à chaque niveau d'imbrication. Les capacités de comptage des programmes, et d'autant plus que les gens sont limités, compter "jusqu'au tapis" est loin d'être toujours possible. Il peut facilement s'avérer que le joueur a compté jusqu'à une position où il a une bonne évaluation du terrain de jeu, mais littéralement au niveau suivant (illisible), l'adversaire a la possibilité de faire un tel mouvement qui change radicalement l'estimation de la position en sens inverse.
Qui est à blâmer et que faire? La complexité de calcul est à blâmer pour la traversée complète de l'arbre; il est proposé de lutter en coupant les branches inutiles. Si le joueur qui évalue la position voit qu'une branche de l'arborescence d'options:
ou moins rentable pour elle que d'autres branches qui ont déjà été analysées,
ou plus avantageux pour l'adversaire que d'autres branches qui ont déjà été analysées,
alors le joueur défausse cette branche, ne perd pas de temps et de ressources à considérer les sous-options de cette branche évidemment pire pour lui.
Cela vous permet d'allouer plus de ressources informatiques pour calculer des branches plus favorables à une plus grande profondeur de rendu dans l'arborescence des options. Dans le processus d'évaluation du terrain de jeu à différents niveaux de l'arborescence des options, le joueur fonctionne avec deux coefficients changeant dynamiquement -
alpha (la valeur du SFD qui est rencontrée de manière minimale dans la branche - c'est-à-dire plus favorable pour le joueur minimisant) et
beta (la valeur de la SFD la plus rencontrée dans la branche - c'est-à-dire plus favorable pour le joueur maximisant). À chaque niveau, la comparaison du SFD de la position actuelle avec
les coefficients
alpha et
bêta permet de balayer (sans les calculer complètement) des branches
moins favorables pour le joueur évaluant la position et / ou
plus avantageuses pour son adversaire.
Il s'agit d'un découpage alpha bêta.
Fonction minimax récursive avec écrêtage alpha bêta
2048 avec AI est implémenté en tant qu'application Excel avec des macros VBA, c'est ainsi que l'algorithme minimax avec écrêtage alpha beta ressemble à un élémentaire visuel méprisable. Ovolve code dans java-script function AI(grid) { this.grid = grid; }
Fonction d'évaluation statique
Étant donné qu'à chaque niveau de l'arborescence des options, vous devez évaluer le terrain de jeu (afin de décider pour lequel des joueurs, la position estimée est en fait plus avantageuse), vous devez décider selon quels critères pour distinguer une bonne position d'une mauvaise position.
Nous supposons que le joueur maximisant est la personne (ou l'IA) qui décide dans laquelle des 4 directions (haut, gauche, droite, bas) déplacer toutes les tuiles. Un joueur minimisant est ce sous-programme insidieux qui génère au hasard 2 ou 4 dans les endroits les plus inappropriés.
L'OFS est compilé du point de vue d'un acteur maximisant. Plus la note SFD est élevée pour le terrain de jeu, meilleure est la position du «maximaliste». Le plus bas - plus la position sur la planche est agréable pour le "minimaliste".
Dans le cas de 2048 - quels facteurs sont considérés comme favorables à celui qui déplace les tuiles?
Monotonie
Tout d'abord, il est souhaitable que les carreaux soient disposés dans l'ordre croissant / décroissant dans certaines directions. Si cela n'est pas fait, lorsque de nouvelles tuiles sont générées, le terrain de jeu sera rapidement obstrué par des tuiles disposées au hasard de différentes tailles, qui ne peuvent pas être immédiatement connectées normalement les unes aux autres.
Dans le district fédéral de Sibérie, vous devez regarder dans les 4 directions (de haut en bas, de gauche à droite, de droite à gauche, de bas en haut) et calculer où les tuiles sont une progression décroissante ou croissante. Si en progression il y a des tuiles qui ne rentrent pas dans la série générale, cela réduit le coefficient numérique de monotonie. Ensuite, parmi les 4 coefficients pour toutes les directions, le meilleur est sélectionné, qui est pris en compte dans la valeur totale du district fédéral sibérien.
Douceur

De plus, il serait plus préférable que la progression de la position debout dans une rangée de tuiles ne soit pas seulement croissante, mais non décroissante (ou au lieu de diminuer la ligne, il est préférable de ne pas augmenter), c'est-à-dire que c'est bien lorsque les mêmes tuiles sont à proximité, ce qui leur permet de s'effondrer en une seule, de gagner des points et augmenter l'espace libre sur le terrain de jeu.
Par conséquent, le district fédéral de Sibérie recherche les mêmes tuiles adjacentes sur le terrain de jeu et prend en compte le nombre de ces paires dans un coefficient spécial.
Cellules vides

Évidemment, plus il y a d'espace libre, plus il y a de marge de manœuvre et moins il y a de chances de perdre rapidement.
SFO considère les cellules vides sur le terrain et plus celles-ci, la position est considérée comme plus rentable pour le joueur maximisant.
Tuile maximum
Étant donné que la principale chose dans ce jeu est d'obtenir une grande tuile sur le terrain, plus c'est mieux - 2048, 4096, 8192 (ou tout ce pour quoi vous avez la force et la patience), les options où la valeur maximale de la tuile est la plus élevée doivent être considérées comme le SFD le plus rentable.
District fédéral sibérien pour 2048
Implémentation du District fédéral sibérien en tant que macro VBA Ovolve code dans java-script function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
L'application Excel elle-même
peut être téléchargée depuis Google .
La fonctionnalité de l'application est décrite
dans un article précédent, où l'IA joue en utilisant la méthode Monte Carlo . La solution d'aujourd'hui a été ajoutée au Monte Carlo existant.
Tous les articles des séries AI et 2048
- Monte Carlo
- Écrêtage Minimax + alpha beta
- En attente du maximum
- Réseau de neurones