Fonctionnement de la cryptographie à courbe elliptique dans TLS 1.3

Quelques alertes aux lecteurs:

Afin de simplifier (quelque peu) le processus de description et de resserrer le volume de l'article que nous allons écrire, il est essentiel de faire une remarque significative et d'énoncer tout de suite la contrainte principale - tout ce que nous allons vous dire aujourd'hui sur la pratique côté de la problématique n'est viable qu'en termes de TLS 1.3. Cela signifie que, même si votre certificat ECDSA fonctionnerait toujours dans TLS 1.2 si vous le souhaitiez, offrant une compatibilité descendante, la description du processus de prise de contact réel, des combinaisons de chiffrement et des benchmarks client-serveur ne couvre que TLS 1.3. Bien sûr, cela ne concerne pas la description mathématique des algorithmes derrière les systèmes de cryptage modernes.

Cet article n'a été écrit ni par un mathématicien ni par un ingénieur - bien que ceux-ci aient aidé à trouver un moyen de contourner les mathématiques effrayantes et aient examiné cet article. Un grand merci aux employés de Qrator Labs.

(Courbe elliptique) D iffie- H ellman (Ephémère)

L'héritage Diffie - Hellman au 21e siècle

Bien sûr, cela n'a commencé ni avec Diffie ni Hellman. Mais pour fournir un calendrier correct, nous devons souligner les dates et événements principaux.

Il y avait plusieurs personnages majeurs dans le développement de la cryptographie moderne. Plus particulièrement, Alan Turing et Claud Shannon ont tous deux consacré une quantité incroyable de travail au domaine de la théorie du calcul et de la théorie de l'information ainsi qu'à la cryptanalyse générale, et Diffie et Hellman sont officiellement reconnus pour avoir proposé l'idée de clé publique (ou soi-disant asymétrique) (bien que l'on sache qu'au Royaume-Uni, des avancées importantes en cryptographie sont restées secrètes pendant très longtemps), faisant de ces deux messieurs des pionniers.

Dans quoi exactement?

Eh bien, cela peut sembler particulier; cependant, avant le 6 novembre 1976, le public ne connaissait pas les systèmes de chiffrement à clé publique. Whitfield Diffie et Martin Hellman (et, en fait, Ralph Merkle) - les mathématiciens, les informaticiens et les passionnés, ainsi que les cryptologues ont été les premiers.

Pour ceux qui ne le savent pas - en raison du rôle que la cryptanalyse a pris pendant la Seconde Guerre mondiale et de son énorme impact sur la confidentialité des informations, les deux pays qui pensaient avoir les connaissances les plus avancées en cryptographie - les États-Unis et le Royaume-Uni ont inclus le cryptage dans leurs listes de munitions et ont exploité une interdiction d'exportation sévère (affaiblissant simultanément la mise en œuvre du cryptage pour un usage domestique privé et commercial). Pour cette raison, les chercheurs britanniques travaillant sur la technique d'échange de clés asymétriques au siège des communications gouvernementales et développant un schéma analogue n'ont été reconnus pour cette invention qu'en 1997, lorsque les restrictions sur les algorithmes de cryptographie et leur description ont été rendues inefficaces.

Revenons à nos deux inventeurs - qu'est-ce qui a particulièrement révolutionné Diffie et Hellman?

Jetons un coup d'œil à leur article original, illustrant parfaitement le saut géant qu'ils ont introduit (même théoriquement avec leur document de recherche):

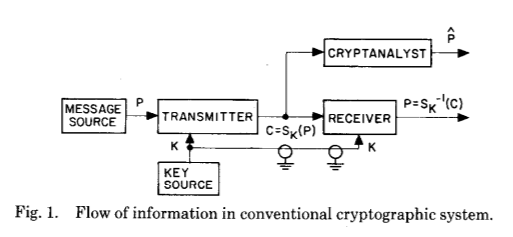
Et le suivant:

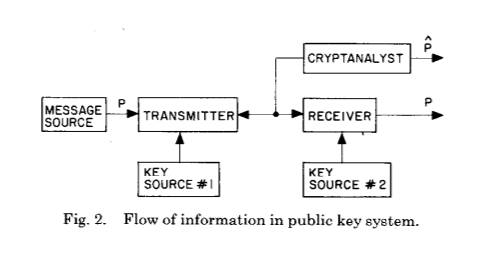
Ces deux images illustrent parfaitement l'énorme changement que Whitfield Diffie et Martin Hellman ont introduit après des siècles d'évolution de la cryptographie et de la cryptanalyse - l'établissement d'une clé secrète partagée à la suite d'un calcul cryptographique.

Jetons un coup d'œil à une autre bonne image avec des couleurs:



Il explique ce qui se passe. Avant l'invention de l'accord de clé Diffie et Hellman, il n'y avait qu'une seule clé symétrique - elle était utilisée à la fois pour crypter et décrypter le message. Si vous voulez donner à quelqu'un une telle «clé», elle doit être transférée sur un canal «sécurisé». Vous pouvez imaginer immédiatement toutes les restrictions d'un tel schéma de génération précédente - vous avez besoin d'un canal sécurisé déjà établi, vous ne pouvez pas réutiliser la clé et, idéalement, la longueur de la clé devrait être la même que la longueur du message.

Claude Shannon dans son ouvrage classé en temps de guerre « Communication Theory of Secrecy Systems » a prouvé que tous les chiffrements théoriquement incassables doivent avoir les mêmes exigences que le pavé à usage unique - connu sous le nom de chiffrement Vernam, par l'auteur de ce chiffrement symétrique à flux polyalphabétique.

Encore une fois, nous allons jeter un œil au document original:


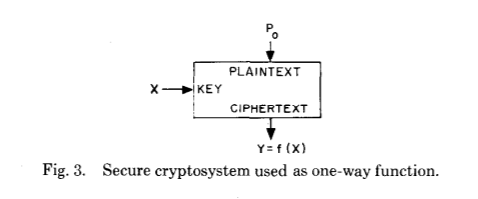
Avant d'aller plus loin, posons-nous la question suivante: comment deux êtres humains, même brillants, ont-ils trouvé une amélioration aussi significative dans un domaine appliqué avec une telle histoire, en particulier en temps de guerre?
Eh bien, à cause de:

• Théorie de l'information , formulée par Claude Shannon;
• Théorie du calcul influencée notamment par Alonzo Church, John von Neumann et Alan Turing;
• Et, plus important encore, la théorie de la calculabilité basée principalement sur le travail de Turing, que nous pourrions dire tous développé et mûri à la même période du 20e siècle. Diffie et Hellman ont tous deux mentionné Claude Shannon comme l'influenceur le plus important de leur travail.

La « sécurité universelle » de Lenstra illustre la quantité d'énergie nécessaire pour «casser» le cryptosystème symétrique avec différentes longueurs de clé. Il s'est avéré que briser une clé de courbe elliptique de 228 bits nécessiterait la même quantité d'énergie nécessaire pour faire bouillir toute l'eau sur Terre. Il n'est cependant valable que si l'on considère les algorithmes et le matériel connus, car à strictement parler, personne ne sait s'il existe des algorithmes ou du matériel beaucoup plus efficaces. La clé EC 228 bits est comparable à la clé RSA longue de 2380 bits, plus à ce sujet plus tard. Bien que dans cette estimation, les clés RSA et EC soient utilisées dans un schéma de chiffrement asymétrique, ces longueurs de clé sont quelque peu équivalentes à une clé de chiffrement symétrique à 128 bits.

Il est facile d'imaginer que quelque chose de «difficile à calculer» nécessiterait beaucoup d'énergie et / ou de temps pour le calcul. Nous avons tendance à penser que les ordinateurs peuvent «tout calculer», mais il s'avère que ce n'est pas vrai. Premièrement, il existe des exemples indécidables, comme le problème d'arrêt, bien que dans le domaine de la cryptographie, nous puissions éviter cet écueil. Deuxièmement, si nous considérons le temps nécessaire à l'exécution d'un algorithme particulier, il peut être arbitrairement élevé. C'est ce que nous exploitons en cryptographie. Un problème est considéré comme «facile» à calculer si le temps requis pour exécuter l'algorithme respectif dépend de la taille d'entrée (mesurée en bits) comme un polynôme:$$ $ en ligne $ T (n) = O (n ^ k) $ en ligne $ , pour une constante positive$$ $ en ligne $ k $ en ligne $ . Dans le domaine de la théorie de la complexité informatique , ces problèmes forment la classe de complexité P.

La classe de complexité P est presque centrale, car elle représente le problème pour lequel il existe un algorithme de temps polynomial déterministe. Une autre classe de complexité est le NP (les problèmes «difficiles» à calculer), représentant un ensemble de problèmes de décision, c'est-à-dire des problèmes nécessitant une réponse «oui» ou «non», qui ont une preuve vérifiable en temps polynomial. Vous voyez le mot «preuve» ici? C'est là que nous arrivons aux fonctions de trappe, appartenant à la classe de complexité NP.


Crédits: xkcd

Fonctions unidirectionnelles; Fonctions de trappe

Par définition, une fonction unidirectionnelle est une fonction qui est facile à calculer sur chaque entrée mais qui est difficile à inverser, c'est-à-dire à calculer l'entrée d'origine uniquement pour la sortie. «Facile» et «difficile» font référence aux définitions de la théorie de la complexité de calcul ci-dessus. Il est intéressant de noter que l'existence de fonctions unidirectionnelles n'est pas (mathématiquement) prouvée car leur existence prouverait que les classes de complexité P et NP ne sont pas égales, alors que P égal NP ou non est de nos jours un problème ouvert. Donc, gardez à l'esprit que toute la cryptographie moderne repose sur des hypothèses non prouvées.

Maintenant, dans leur article original, Diffie et Hellman présentent une autre génération des fonctions à sens unique qu'ils appelaient «fonctions de trappe». En quoi diffèrent-ils?
Comme ils l'expliquent dans leur document historique:

Dans un cryptosystème à clé publique, le chiffrement et le déchiffrement sont régis par des clés distinctes, E et D, de sorte que le calcul de D à partir de E est impossible à calculer (par exemple, nécessitant$$ $ en ligne $ 10 ^ {100} $ en ligne $ instructions). La clé de chiffrement E peut être divulguée [dans un répertoire] sans compromettre la clé de déchiffrement D. Cela permet à tout utilisateur du système d'envoyer un message à tout autre utilisateur chiffré de telle sorte que seul le destinataire prévu est capable de le déchiffrer. .. Le problème de l'authentification est peut-être un obstacle encore plus sérieux à l'adoption universelle des télécommunications pour les transactions commerciales que les problèmes de distribution des clés ... [il] ... est au cœur de tout système de contrats et de facturation.

Par convention, les caractères de cryptographie «Alice» et «Bob» (à la recherche d'une communication sécurisée) sont fréquemment utilisés pour expliquer le concept de clé publique. Alice et Bob s'entendent sur de grands nombres entiers$$ $ en ligne $ n $ en ligne $ et$$ $ en ligne $ g $ en ligne $ avec$$ $ en ligne $ 1 <g <n $ en ligne $ . La sélection a un impact sur la sécurité du système. «Le module$$ $ en ligne $ n $ en ligne $ devrait être un premier choix; plus important encore$$ $ en ligne $ (n-1) / 2 $ en ligne $ devrait également être un premier <...> et$$ $ en ligne $ g $ en ligne $ devrait être une racine modulo primitive$$ $ en ligne $ n $ en ligne $ <...> [et]$$ $ en ligne $ n $ en ligne $ doit être <...> d'au moins 512 bits. »Le protocole Diffie - Hellman peut être énoncé sous forme élémentaire en 5 étapes.

1. Alice choisit$$ $ en ligne $ x $ en ligne $ (un grand nombre aléatoire) et calcule$$ $ inline $ X = g ^ x \ bmod n $ inline $
2. Bob choisit$$ $ en ligne $ y $ en ligne $ (un grand nombre aléatoire) et calcule$$ $ inline $ Y = g ^ y \ bmod n $ inline $
3. Alice envoie$$ $ en ligne $ X $ en ligne $ à Bob, tandis que Bob envoie$$ $ en ligne $ Y $ en ligne $ à Alice (ils gardent$$ $ en ligne $ x $ en ligne $ et$$ $ en ligne $ y $ en ligne $ secret les uns des autres)
4. Alice calcule$$ $ inline $ k = Y ^ x \ bmod n $ inline $
5. Bob calcule$$ $ inline $ k '= X ^ y \ bmod n $ inline $

En conséquence, Alice et Bob ont la même valeur$$ $ inline $ k = k '$ inline $ qui sert de secret partagé.

La fonction de trappe est une fonction unidirectionnelle qui permet de trouver son inverse si l'on dispose d'une information spéciale appelée «trappe». Cela semble facile, mais il était plutôt difficile de trouver de telles fonctions - la première méthode possible a été trouvée dans la mise en œuvre d'un algorithme de chiffrement asymétrique par cryptographie à clé publique nommé RSA d'après ses créateurs: Ron Rivest, Adi Shamir et Leonard Adleman.

RSA

Dans RSA, la dureté de l'inversion de la fonction est basée sur le fait que l'affacturage (trouver les multiplicateurs premiers d'un nombre) prend beaucoup plus de temps que la multiplication, ou devrions-nous dire ici qu'aucune méthode en temps polynomial pour factoriser de grands entiers sur un ordinateur classique Cependant, il n'a pas été prouvé qu'il n'en existe pas.

Dans RSA, comme dans tout autre système de chiffrement à clé publique, il existe deux clés: publique et privée. RSA prend le message d'entrée (représenté sous la forme d'une chaîne de bits) et lui applique une opération mathématique (exponentiation modulo un grand entier) pour obtenir un résultat qui ne se distingue pas du hasard. Le déchiffrement prend ce résultat et applique une opération similaire pour récupérer le message d'origine. En cryptographie asymétrique, le cryptage est effectué avec la clé publique et le décryptage avec la clé privée.

Comment? Parce que les opérandes appartiennent à un groupe cyclique fini (un ensemble d'entiers avec multiplication en arithmétique modulaire). Les ordinateurs ne traitent pas très bien les nombres arbitrairement grands, mais, heureusement, notre groupe cyclique d'entiers consiste à effectuer une opération appelée «boucler» - un nombre supérieur au maximum autorisé est enroulé autour d'un nombre dans la plage valide que nous exploitons . Cela nous permet de fonctionner avec des touches de longueur «pas plus longue que». Dans la cryptographie à courbe elliptique, des groupes cycliques (multiplicatifs) sont également utilisés mais construits un peu différemment comme nous le verrons plus loin.

Fondamentalement, RSA prend deux grands nombres premiers et les multiplie pour obtenir le soi-disant module. Tous les autres nombres à traiter résident entre zéro et le module. Le module doit faire partie de la clé publique et sa longueur en bits détermine la longueur de la clé. La deuxième partie de la clé publique est un nombre choisi entre zéro et le totient d'Euler (l'implémentation RSA moderne prend le totient de Carmichael au lieu d'Euler) du module avec quelques restrictions supplémentaires. Enfin, la clé privée doit être calculée en résolvant une équation modulaire. Pour crypter un nombre, nous l'élévons simplement à la puissance égale à la clé publique, et pour décrypter un nombre, nous l'élévons à la puissance égale à la clé privée. Grâce à la nature cyclique du groupe, nous récupérons le nombre initial.

Il y a deux problèmes importants avec le RSA de nos jours, l'un étant une conséquence de l'autre. Au fur et à mesure que la longueur d'une clé (c'est-à-dire le nombre de ses bits) augmente, le facteur de complexité ne croît pas aussi vite qu'on pourrait s'y attendre. En effet, il existe un algorithme de factorisation sous-exponentiel (mais toujours super-polynomial ). Ainsi, afin de maintenir un niveau de sécurité approprié, la longueur de la clé RSA doit augmenter un peu plus rapidement que la longueur de la clé ECC. C'est pourquoi les clés RSA les plus répandues de nos jours ont une longueur de 2048 ou 3072 bits.

Un peu plus tard, nous verrons en chiffres comment la longueur de la clé affecte l'efficacité globale du cryptosystème en comparant les certificats RSA et ECDSA signés avec l'autorité Let's Encrypt.

( C urve elliptique) Algorithme de S ignature numérique

La recherche d'une meilleure fonction de trappe a finalement conduit les cryptographes à évoluer activement dans la branche des mathématiques du milieu des années 80 dédiée aux courbes elliptiques.

Ce serait la tâche ultime de décrire la cryptographie à courbe elliptique dans un article, nous ne le ferons donc pas. Examinons plutôt une fonction de trappe à courbe elliptique basée sur le problème du logarithme discret.

Il existe de nombreuses amorces et des introductions plus approfondies dans la cryptographie à courbe elliptique, et nous recommandons particulièrement "ECC: une introduction douce" d'Andrea Corbellini si vous êtes intéressé par les mathématiques.

Ce qui nous intéresse, ce sont des paramètres plutôt «simples».

La courbe elliptique est définie par une équation comme celle-ci:$$ $ inline $ y ^ 2 = x ^ 3 + ax + b $ inline $
Une telle courbe est nécessaire pour construire un sous-groupe cyclique sur un champ fini. Par conséquent, les paramètres suivants sont utilisés:

• Le premier$$ $ inline $ p $ inline $ qui spécifie la taille du champ fini;
• Les coefficients$$ $ inline $ a $ inline $ et$$ $ en ligne $ b $ en ligne $ de l'équation de la courbe elliptique;
• Le point de base$$ $ en ligne $ g $ en ligne $ qui génère le sous-groupe mentionné;
• La commande$$ $ en ligne $ n $ en ligne $ du sous-groupe;
• Le cofacteur$$ $ en ligne $ h $ en ligne $ du sous-groupe.

En conclusion, les paramètres de domaine de nos algorithmes sont le sextuplet$$ $ inline $ (p, a, b, G, n, h) $ inline $ .
Ces courbes elliptiques fonctionnent sur le champ fini$$ $ inline $ \ mathbb {F} _p $ inline $ , où$$ $ inline $ p $ inline $ est un nombre premier assez grand. Nous avons donc un ensemble d'entiers modulo$$ $ inline $ p $ inline $ , où des opérations telles que l'addition, la soustraction, la multiplication, l'inverse additif, l'inverse multiplicatif sont possibles. L'addition et la multiplication fonctionnent de manière similaire à l'arithmétique modulaire ou dite «d'horloge» que nous avons vue dans les «enveloppements» RSA.
Étant donné que la courbe est symétrique par rapport à l'axe des x, étant donné n'importe quel point$$ $ en ligne $ P $ en ligne $ , nous pouvons prendre$$ $ inline $ −P $ inline $ être le point en face d'elle. Nous prenons$$ $ inline $ −O $ inline $ être juste$$ $ en ligne $ O $ en ligne $ .
L'addition pour les points de courbe est définie de manière à ce que les points donnés$$ $ en ligne $ P $ en ligne $ et$$ $ en ligne $ Q $ en ligne $ , nous pouvons tracer une ligne coupant ces deux points et une courbe entrecroisée dans un troisième point$$ $ en ligne $ R $ en ligne $ pour que$$ $ en ligne $ P + Q = -R $ en ligne $ et$$ $ en ligne $ P + Q + R = 0 $ en ligne $ .

Jetons un coup d'œil à l' explication de Marc Hughes :

Une ligne de pente constante qui se déplace le long de la surface du tore est montrée ci-dessus. Cette ligne passe par deux points entiers sélectionnés au hasard sur la courbe.



Pour ajouter deux points sur le graphique, tracez une ligne à partir du premier point sélectionné$$ $ en ligne $ P $ en ligne $ au deuxième point sélectionné$$ $ en ligne $ Q $ en ligne $ et prolonger la ligne jusqu'à ce qu'elle coupe un autre point du graphique$$ $ en ligne $ -R $ en ligne $ , en l'étendant au-delà des limites de la parcelle si nécessaire.

Une fois que vous avez intercepté un point entier, réfléchissez le point verticalement au milieu du graphique (une ligne pointillée orange) pour trouver le nouveau point$$ $ en ligne $ R $ en ligne $ sur le graphique. Par conséquent$$ $ en ligne $ P + Q = R $ en ligne $ .

La multiplication par un scalaire est désormais triviale:$$ $ en ligne $ n \ cdot P = P + P + P + \ points + P $ en ligne $ (voici$$ $ en ligne $ n $ en ligne $ summands).

La fonction de trappe se situe ici dans le problème du logarithme discret (pour les courbes elliptiques), et non dans la factorisation que nous avons examinée dans la section RSA. Le problème est: si nous savons$$ $ en ligne $ P $ en ligne $ et$$ $ en ligne $ Q $ en ligne $ , c'est quoi$$ $ en ligne $ k $ en ligne $ , que$$ $ en ligne $ Q = k \ cdot P $ en ligne $ ?

Le problème de factorisation (sous-jacent au RSA) et le logarithme discret pour les courbes elliptiques (qui est la base de l'ECDSA et de l'ECDH) sont censés être difficiles, c'est-à-dire qu'il n'y a pas d'algorithmes connus pour résoudre ce problème en temps polynomial pour une clé donnée longueur.

Alors que, généralement, tout le monde aurait honte de mélanger l'échange de clés (ECDH) avec l'algorithme de signature (ECDSA), nous devons expliquer comment ils fonctionnent ensemble. Un certificat TLS moderne contient une clé publique, dans notre cas, de la paire de clés générée par l'algorithme de courbe elliptique, généralement signée par une autorité de niveau supérieur. Le client vérifie la signature du serveur et obtient le secret partagé. Le secret partagé est utilisé dans un algorithme de chiffrement symétrique, tel que AES ou ChaCha20. Cependant, le principe reste le même: convenir de paramètres de domaine (le sextuplet), obtenir la paire de clés, où la clé privée est un entier sélectionné au hasard (le multiplicande de$$ $ en ligne $ Q = k \ cdot P $ en ligne $ ), et la clé publique est un point sur la courbe. Les algorithmes de signature utilisent le point de base$$ $ en ligne $ g $ en ligne $ , qui est un générateur pour un sous-groupe de grand ordre premier$$ $ en ligne $ n $ en ligne $ , de telle sorte que$$ $ inline $ n \ cdot G = 0 $ inline $ , où 0 est l'élément d'identité. La signature prouve que la connexion sécurisée est établie avec la partie authentique - un serveur qui a le certificat TLS (clé publique) signé par une autorité de certification pour le nom de serveur donné.

(EC) DH (E) + ECDSA = Forme de prise de contact actuelle

Dans TLS moderne (1.3), le client et le serveur génèrent leur paire de clés publique-privée à la volée, tout en établissant la connexion, cela s'appelle la version éphémère de l'échange de clés. Les bibliothèques TLS de navigateur les plus populaires le prennent en charge. La plupart du temps, ils utilisent la courbe elliptique Edwards 25519 , introduite par Daniel J. Bernstein (djb), offrant une sécurité de 128 bits. Depuis 2014, openssh utilise cette courbe pour la création de paires de clés. En 2019 cependant, les navigateurs ne prennent toujours pas en charge les sessions TLS avec des serveurs ayant un certificat avec une clé publique EdDSA.

Mais revenons à la façon dont les choses fonctionnent à la fin de 2019 avec TLS 1.3.

Les mécanismes d'échange de clés dans TLS 1.3 sont limités aux bases (EC) DH (E) (avec le x25519 est celui pris en charge dans les bibliothèques TLS côté client des navigateurs les plus populaires ainsi que dans les bibliothèques TLS côté serveur, comme OpenSSL, que nous inspecterons un peu plus tard), et la liste des suites de chiffrement ne contient que trois entrées: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 et TLS_CHACHA20_POLY1305_SHA256. Pour ceux d'entre vous qui savent comment les suites de chiffrement ont été nommées dans la version TLS 1.2, il est évident que le mécanisme d'échange de clés est désormais «détaché» du nom de la suite de chiffrement, les modes d'échange RSA statique et Diffie - Hellman statique étant également supprimés de la spécification entièrement. Même la reprise de session basée sur PSK est effectuée via ECDHE dans TLS 1.3. Cela est également vrai pour les paramètres DH personnalisés, qui ne sont pas autorisés pour le moment, ne laissant que ceux généralement acceptés comme étant sécurisés dans la spécification de protocole finale.

Il est intéressant de noter qu'il existe une différence assez importante dans le fonctionnement actuel des algorithmes de chiffrement asymétriques. Avec les certificats ECC (et ECDSA en particulier), nous utilisons des clés plus petites pour atteindre des niveaux de sécurité «pratiques», par rapport à RSA. Cela permet d'utiliser un algorithme de chiffrement asymétrique plus fort et des mécanismes d'échange de clés sur les petits appareils et parfois même dans des choses qui ne sont généralement pas considérées comme un appareil (carte à puce).

Tout d'abord, il faut mentionner ce que signifie «cryptosystème hybride» en termes de TLS 1.3.
Un cryptosystème hybride est celui qui utilise un cryptage asymétrique (clé publique) pour établir un secret partagé, qui est en outre utilisé comme clé dans un flux symétrique ou un chiffrement par bloc.

Deuxièmement, l'infrastructure à clé publique et les certificats. Il est intéressant de noter que dans son interview de 2004, Martin Hellman a mentionné un «héros méconnu» Loren Kohnfelder, dont la thèse de baccalauréat du MIT a introduit une structure arborescente de ce que nous connaissons aujourd'hui sous le nom d'infrastructure à clé publique. Néanmoins, revenons aux certificats.

Le fait que le serveur possède réellement la clé privée est assuré par sa signature, qui peut être vérifiée avec la clé publique du serveur. Et le certificat garantit qu'une certaine clé publique appartient à un serveur spécifique. Cela signifie que vous établissez une communication sécurisée avec la partie spécifique et non avec un imposteur. Votre banque, pas un cybercriminel. Dans TLS 1.3, il y a une amélioration significative par rapport au format de négociation précédent - le serveur signe toutes les informations dont il dispose jusqu'à présent: le bonjour du client et le bonjour du serveur, y compris le chiffrement négocié. Jetons un coup d'œil à la section correspondante du RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

Dans TLS 1.3, le client envoie immédiatement le partage de clé (avec les paramètres nécessaires), les algorithmes de signature dans le premier message (Client Hello). Les clés nécessaires pour échanger avec le serveur sont créées en arrière-plan, sans que l'utilisateur ne s'en aperçoive. Ils sont ensuite échangés avec le serveur pour créer un secret commun, à partir de clés secrètes pré-maître qui ont été établies lorsque le serveur a envoyé son message (Server Hello) répondant au client.
Du côté «Server Hello», vous pouvez voir le certificat * transféré au client, ainsi que la partie Certificate Verify * qui vérifie que la partie possède la clé privée pour l'entrée de clé publique correspondante et crée la clé de session (symétrique) si tout se passe comme prévu - ce qui signifie que la partie qui demande les données (client) a vérifié avec succès la partie répondante (serveur), créant ainsi un secret commun.

Il y a deux opérations essentielles cachées dans ces transmissions - la création de signature et la vérification de signature. Celles-ci sont faites des deux côtés de la communication, car la «signature» est essentiellement une preuve que la partie a effectivement la clé privée correspondant à la clé publique, que les données proviennent du signataire et que le message n'a pas été modifié en transit.

Avec RSA, comme nous le verrons plus loin, l'opération de signature est la plus coûteuse. Puisque nous signons avec une clé longue de 2048 ou 3072 bits, une telle opération charge le serveur de manière significative, bien plus qu'elle ne charge le client vérifiant une telle signature.

Avec ECDSA, nous avons des clés plus petites (nous allons regarder l'ECDSA avec NIST P-256 (ou secp256v1)) mais des opérations plus complexes. En conséquence, il pourrait être considéré comme le RSA «à l'envers» - le client est le plus chargé, par le calcul de vérification de signature, tandis que le serveur gère facilement la création de signature. Les mesures le vérifient, voir la section «Un peu de référence».

Cet effet fait évoluer facilement Internet de nos jours - car les clients modernes sont presque aussi puissants que les serveurs (en ne tenant compte que de la fréquence centrale du processeur), de sorte qu'ils pourraient effectivement prendre à nu l'opération coûteuse. Le serveur, à son tour, peut utiliser les capacités libérées pour créer plus de signatures et établir plus de sessions.

Encryptons la signature du certificat

Donc, afin de fournir au lecteur un peu d'instructions pratiques et pratiques sur la façon de créer un serveur compatible TLS avec la paire de clés ECDSA signée par l'autorité Let's Encrypt, nous avons décidé d'illustrer un processus complet de création d'une paire de clés nécessaire pour créer une CSR (demande de signature de certificat) pour Let's Encrypt et, par conséquent, obtenir le certificat ECDSA nécessaire pour notre serveur.

Nous devons générer une clé privée pour continuer. Nous utiliserons la bibliothèque OpenSSL.
Le manuel OpenSSL décrit la génération de toutes les clés EC via une commande spéciale, désignée spécialement pour la branche de courbe elliptique de l'algorithme de génération.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Pour vérifier que la bibliothèque OpenSSL a tout fait correctement, nous pouvons exécuter la commande ec .

 openssl ec -in privatekey.pem -noout -text 

La sortie nous montrera la courbe spécifiée avec laquelle la clé a été créée.

La prochaine étape est tout à fait essentielle à la création de la CSR - afin d'ignorer le processus de remplissage de tous les détails nécessaires à l'obtention du certificat, nous avons besoin du fichier de configuration. Heureusement, Mozilla a fait tout le travail pour nous, en introduisant le « générateur de configuration SSL ». Là, vous pouvez choisir parmi toutes les options de serveur disponibles. La pure configuration OpenSSL, particulièrement absente de la page du générateur, ressemblerait à ceci:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Remarque: il n'est pas nécessaire d'avoir le CNF - si vous ne le faites pas, il vous sera demandé de remplir ces détails dans la ligne de commande.

Maintenant, suivez la création d'une RSE elle-même. Ici, nous avons une commande OpenSSL pratique.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

Nous pouvons également vérifier l'exactitude d'un CSR nouvellement créé.

 openssl req -in csr.pem -noout -text -verify 

Ici, nous sommes arrivés à une phase finale - en utilisant un client ACME, certbot, pour transmettre notre demande de signature de certificat à Let's Encrypt.

Certbot vous aide à obtenir le certificat nécessaire et propose de nombreuses options. Ici, si vous êtes nouveau dans le cryptage à clé publique et l'infrastructure PKI que nous avons en 2019, vous feriez mieux d'utiliser --dry-run avant d'essayer d'obtenir le certificat pour n'importe quel domaine de la vôtre.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

Dans ce cas, le client certbot vérifie que la liste des domaines demandés (dans la ligne de commande) correspond aux domaines répertoriés dans la demande de signature de certificat. Dans la commande --dns-somednsprovider se trouve un peu un mensonge, car il existe de nombreuses façons de prouver à Let's Encrypt que vous êtes en possession d'une partie particulière du trafic Internet. Cependant, si vous utilisez un fournisseur d'hébergement cloud public, par exemple DigitalOcean, Hetzner, Amazon, Azure, n'importe quoi - il y aurait probablement un moyen plus naturel de fournir les informations nécessaires, car votre fournisseur a déjà créé un outil d'intégration.

Après, si vous êtes sûr de l'exactitude des paramètres que vous utilisez pour transmettre votre CSR à Let's Encrypt via un client certbot - excluez le paramètre --dry-run de votre commande et continuez.

En cas de succès, le client produirait plusieurs certificats en sortie: le certificat signé lui-même, les certificats racine et intermédiaire, et la combinaison de ces derniers en tant que dernière chaîne de certificats nommés, le tout au format de fichier .pem.

OpenSSL a une commande que nous pourrions utiliser pour inspecter les certificats:

 openssl x509 -in chainfilepath.pem -noout -text 

À ce stade, il devient évident que Let's Encrypt a signé le certificat à l'aide du résumé SHA256. De plus, la signature ECDSA Root et Intermediates relève de la section «Fonctionnalités à venir», ce qui signifie que vous n'obtiendrez actuellement que des intermédiaires RSA. Mais ça va puisque vous utilisez toujours la clé publique ECDSA.

À la fin de cette section, nous aimerions dire quelque chose à propos de la longueur des clés. En sécurité de l'information, il est courant de dire que le niveau de sécurité est 2 ^ x, où x est la longueur de bit (RSA est un peu une exception ici, car il se développe un peu plus lentement qu'exponentiellement). Pour approximer la façon dont les clés utilisées pour les différents algorithmes se correspondent, nous nous référons à la page wiki OpenSSL.
Comme vous pouvez le voir, les différences sont assez marquées. Bien qu'avec Let's Encrypt, nous n'avons pu obtenir aucun certificat signé en dehors des clés de courbe elliptique 256 (secp256v1) et 384 (secp384r1).

Problèmes connus et exceptions, et LA NSA

Crédits: xkcd

Le problème central de l'utilisation de la cryptographie à courbe elliptique au fil des ans était probablement la nécessité d'un générateur de nombres aléatoires très soigneusement conçu, afin de créer des clés de niveau de sécurité requis.

Il y a eu un énorme scandale autour de l'algorithme Dual_EC_DRBG (générateur de bits aléatoires déterministes à courbe elliptique double), qui a mis plusieurs années à se résoudre. En outre, il existe une incertitude concernant les brevets ECC, car il est connu que beaucoup d'entre eux appartenaient à la société Certicom, qui a été acquise par Blackberry. Il existe également des entreprises connues pour être certifiées pour l'utilisation de l'ECC de Blackberry. Bien sûr, il existe une simple méfiance à l'égard de certaines normes du NIST, qui pourraient ou non être affectées par la NSA ou toute autre institution de contrôle et de surveillance des États-Unis.

Le côté de la mise en œuvre d'un problème est une question entièrement différente. En 2010, la console PlayStation 3 a subi une récupération de clé privée Sony en raison d'une mauvaise mise en œuvre de l'algorithme ECDSA - elles avaient un aléatoire statique qui rendait la fonction de trappe résoluble. OpenSSL a également souffert l'année suivante, cependant, corrigeant rapidement la vulnérabilité qui permettait la récupération d'une clé privée à l'aide d'une attaque temporelle, pour plus d'informations, consultez le document d'origine .

En 2013, lors de la conférence RSA, un groupe de chercheurs a présenté leur « Randomly Failed! »Document sur les vulnérabilités de la classe Java SecureRandom. Un an et demi plus tard, il s'agissait de portefeuilles Bitcoin Android , créés en utilisant pas assez de PRNG sécurisé cryptographiquement.

En raison de graves vulnérabilités en série découvertes, le même août 2013, l'IETF a publié un RFC 6979 , décrivant une génération déterministe de k utilisée dans la création de la clé. Nous pourrions dire qu'une telle mesure a résolu le problème, mais nous ne le ferons pas - à chaque fois que les chercheurs pourraient trouver des problèmes dans de nombreuses implémentations en raison d'une déviation inutile des spécifications du protocole.

À propos de la NSA. Si vous n'avez pas entendu parler de l'histoire de Dual_EC_DRBG - réservez un peu de temps et lisez les articles correspondants, vous ne regretterez pas d'entrer dans les détails. Edward Snowden fait partie de cette histoire car les révélations de 2013 ont prouvé les soupçons antérieurs. Cela a entraîné la perte de confiance de nombreux cryptographes éminents envers le NIST depuis que cette organisation a conçu et décrit de nombreuses courbes et d'autres algorithmes, sous-jacents à l'ECDSA.

La courbe 25519 et la fonction DH de Daniel Bernstein sont la réponse à ces deux problèmes et, comme nous l'avons décrit plus haut, une transition vers EdDSA est lente mais évidente. Même avec les courbes NIST, aucune preuve de leur vulnérabilité n'a encore été trouvée et, comme nous l'avons déjà mentionné, l'expérience liée au hasard a été assez instructive.

Pour conclure cette partie, nous voulons donner la citation de John von Neumann: "Quiconque tente de générer des nombres aléatoires par des moyens déterministes vit, bien sûr, dans un état de péché."

Un peu de référence

Nous avons utilisé un serveur NGINX 1.16.0 avec OpenSSL 1.1.1d pour exécuter ces tests avec divers certificats. Comme nous l'avons mentionné précédemment, Let's Encrypt n'autorise actuellement que les algorithmes prime256v1 et secp384r1 pour les demandes de signature de certificat et ne fournit pas de certificats ECDSA racine et intermédiaire, travaillant probablement sur cette fonctionnalité au moment où nous écrivons cet article.
Comme vous pouvez le voir, pour un seul cœur du processeur Intel® Xeon® Silver 4114 à 2,20 GHz (lancé au troisième trimestre 2017), la différence globale des performances ECDSA par rapport au RSA 2048 largement adopté est de 3,5x.

Jetons maintenant un coup d'œil aux résultats de vitesse OpenSSL du même processeur avec ECDSA et RSA.
Ici, nous pouvons voir une confirmation pour la thèse donnée précédemment des différents coûts de calcul pour les opérations de signe et de vérification d'ECC et de RSA. Par conséquent, actuellement équipé de TLS 1.3 ECC offre une amélioration significative des performances au niveau de sécurité plus élevé, par rapport à RSA. C'est la raison la plus importante pour laquelle nous, chez Qrator Labs, encourageons nos clients à adopter ECDSA. Avec les processeurs modernes, vous obtenez presque la différence de 5 fois en faveur de l'ECDSA.

Si vous êtes intéressé par la façon dont votre CPU effectue des calculs cryptographiques, vous pouvez exécuter une simple commande de openssl speed . Les -rsa , -ecdsa et -eddsa vous donneraient des résultats de référence pour les algorithmes de signature correspondants.

(Superposé) Futur

Crédits: djb

Il est ironique de constater que pendant que nous préparions cet article, Google a annoncé « atteindre la suprématie quantique ». Cela signifie-t-il que nous sommes en danger en ce moment et que tout ce qui s'est développé jusqu'à présent ne fournit aucun secret?

Et bien non.

Comme Bruce Schneier l'a écrit dans son essai pour IEEE Security and Privacy « Cryptography after the Aliens Lands », un énorme coup avec un ordinateur quantique suffisamment puissant pourrait être porté à la cryptographie à clé publique (asymétrique). La cryptographie symétrique serait toujours forte.

Nous voulons citer Bruce Schneier avec ce qui suit:

Il y a un autre scénario futur à considérer, un qui ne nécessite pas d'ordinateur quantique. Bien qu'il existe plusieurs théories mathématiques qui sous-tendent le caractère unidirectionnel que nous utilisons en cryptographie, prouver la validité de ces théories est en fait l'un des grands problèmes ouverts en informatique. Tout comme il est possible pour un cryptographe intelligent de trouver une nouvelle astuce qui facilite la rupture d'un algorithme particulier, nous pourrions imaginer des extraterrestres avec une théorie mathématique suffisante pour briser tous les algorithmes de cryptage. Pour nous, aujourd'hui, c'est ridicule. La cryptographie à clé publique est une théorie entièrement numérique, et potentiellement vulnérable à des extraterrestres plus enclins aux mathématiques. La cryptographie symétrique est tellement confuse non linéaire, si facile à rendre plus complexe, et si facile à augmenter la longueur de clé, que cet avenir est inimaginable. Considérez une variante AES avec un bloc de 512 bits et une taille de clé, et 128 tours. À moins que les mathématiques ne soient fondamentalement différentes de notre compréhension actuelle, cela sera sécurisé jusqu'à ce que les ordinateurs soient faits d'autre chose que de la matière et occupent autre chose que de l'espace.

Mais si l'inimaginable se produit, cela nous laisserait une cryptographie basée uniquement sur la théorie de l'information: les blocs uniques et leurs variantes.

C'est le domaine où, à l'exception de la recherche de défauts de mise en œuvre, la plupart des problèmes peuvent être trouvés. S'il y a un groupe de mathématiciens, cryptanalystes / cryptographes et ingénieurs informatiques bien financés qui travaillent à prouver ou à réfuter certains problèmes mathématiques complexes extraordinaires (comme le P? = NP) et à obtenir des résultats substantiels jusqu'à ce moment, nous pourrions avoir des ennuis. Cependant, de telles avancées dans les théories de l'informatique, de l'information et de la calculabilité sont peu susceptibles d'être cachées, car ce fait écrirait les noms de leurs créateurs sur les pages de l'Histoire et, en particulier, de l'Histoire des manuels Internet, qui n'a pas de prix pour quiconque est intelligent . Ainsi, un tel scénario pourrait être considéré comme presque impossible.

Il n'est pas clair si, dans les 5 prochaines années, il y aura des succès avec l'informatique quantique, bien qu'il existe déjà plusieurs primitives de cryptographie considérées comme adaptées au monde post-quantique: réseaux, basés sur l'isogenèse de la courbe elliptique supersingulaire, hachages et codes. Pour l'instant, les spécialistes de la sécurité ne font que les expérimenter. Cependant, il ne fait aucun doute qu'en cas de besoin, l'humanité utiliserait rapidement de tels algorithmes à grande échelle.

Pour l'instant, la cryptographie basée sur la courbe elliptique semble être un ajustement parfait pour la prochaine décennie, offrant sécurité et performances.