L'hypothèse du premier principe est l'une des questions les plus importantes et les plus complexes en mathématiques. Deux mathématiciens ont résolu une version parallèle de ce problème pour les petits systèmes numériques.

Le 7 septembre, deux mathématiciens ont
publié la preuve d'une version de l'un des problèmes ouverts les plus connus en mathématiques. Le résultat ouvre un nouveau front dans l'étude de l'hypothèse des
nombres premiers jumeaux qui tourmente les mathématiciens depuis plus de cent ans et est associée à certaines des propriétés les plus profondes de l'arithmétique.
"Nous dérapons depuis longtemps et nous manquons d'idées pour cette tâche, il est donc naturel pour quiconque d'avoir de nouvelles idées", a déclaré
James Maynard , un mathématicien d'Oxford.
L'hypothèse du premier jumeau s'applique aux paires de nombres premiers qui diffèrent par 2. Les jumeaux sont les nombres 5 et 7. Et 17 et 19. L'hypothèse stipule qu'il existe un nombre infini de telles paires parmi les nombres naturels. Au cours de la dernière décennie, les mathématiciens ont fait des progrès importants, mais ils sont encore très loin d'une solution complète au problème.
Les auteurs des nouvelles preuves,
Will Savin de l'Université Columbia et
Mark Shusterman de l'Université du Wisconsin à Madison, ont prouvé l'hypothèse d'un monde mathématique plus petit, mais toujours perceptible. Ils ont prouvé sa validité dans le cas d'un système numérique fini dans lequel il n'y a que quelques nombres.
De tels systèmes numériques sont appelés «champs finis». Malgré leur petite taille, ils conservent bon nombre des propriétés mathématiques inhérentes à d'innombrables nombres entiers. Les mathématiciens tentent de trouver des réponses aux questions d'arithmétique dans les domaines finis et espèrent traduire ces résultats en tous les nombres entiers.
"Le rêve ultime, quoique un peu naïf, est qu'une bonne compréhension des propriétés d'un champ fini puisse éclairer le monde des entiers", a déclaré Maynard.
En plus de prouver l'hypothèse des nombres premiers jumeaux, Savin et Shusterman ont trouvé un résultat encore plus surprenant concernant le comportement des nombres premiers dans les petits systèmes numériques. Ils ont prouvé la fréquence exacte avec laquelle les nombres premiers jumeaux apparaissent à de petits intervalles - et ce résultat permet de contrôler de manière extrêmement précise un phénomène tel que les nombres premiers jumeaux. Les mathématiciens rêvent d'obtenir des résultats similaires avec des nombres ordinaires; ils explorent de nouvelles preuves à la recherche d'idées applicables aux nombres premiers sur une droite numérique.
Un nouveau type de prime
La prédiction la plus célèbre de l'hypothèse du premier jumeau est la présence d'un nombre infiniment grand de paires de nombres qui diffèrent par 2. Cependant, cette affirmation est plus générale. Il indique qu'il existe un nombre infini de nombres premiers qui diffèrent par 4 (par exemple, 3 et 7), ou par 14 (293 et 307), ou par n'importe quel nombre que vous spécifiez.
Alfons de Polignac a
fait cette hypothèse sous sa forme moderne en 1849. Au cours des 160 années suivantes, les mathématiciens n'ont pas beaucoup avancé avec lui. Cependant, en 2013, la glace s'est brisée, ou du moins sérieusement fissurée. Cette année-là,
Zhang Ethan a prouvé la présence d'un nombre infiniment grand de paires de nombres premiers, ne différant pas de plus de 70 millions. L'année prochaine, d'autres mathématiciens, dont Maynard et
Terry Tao , ont sérieusement réduit cet écart. Le record actuel est la preuve de l'existence d'un nombre infiniment grand de paires de nombres premiers qui ne diffèrent pas de plus de 246.
Cependant, après cela, les progrès se sont calmés. Les mathématiciens comprennent la nécessité d'une idée complètement nouvelle pour résoudre complètement ce problème. Et les systèmes de nombres finis sont un bon endroit pour chercher cette idée.
Pour construire un champ fini, vous devez d'abord extraire un sous-ensemble fini de nombres à partir de nombres naturels. Vous pouvez, par exemple, prendre les cinq premiers chiffres (ou n'importe quel nombre premier). Et au lieu de représenter des nombres sur une ligne numérique, comme d'habitude, imaginez un nouveau système numérique sous la forme d'un cadran.
L'arithmétique, comme vous l'avez peut-être deviné, commence à fonctionner dans un espace confiné. Que sera 4 + 3 dans un système numérique fini composé de cinq éléments? Nous commençons par 4, comptons trois divisions dans le sens des aiguilles d'une montre et arrivons à 2. La soustraction, la multiplication et la division fonctionnent de la même manière.

Mais seulement il y a un hic. Dans les domaines finis, la définition habituelle d'un nombre premier n'a pas de sens. Dans le dernier champ, tout nombre est divisé par un autre. Par exemple, 7 n'est généralement pas divisible par 3. Mais sur un dernier champ de cinq éléments, il est divisible. C'est parce que sur ce dernier champ, le numéro 7 est équivalent au numéro 12 - ils se terminent tous les deux à la marque 2 du cadran. Par conséquent, 7 divisé par 3 donnera la même chose que 12 divisé par 3 - et 12 divisé par 3 donnera 4.
Par conséquent, l'hypothèse de nombres premiers jumeaux pour les champs finis fait référence à des polynômes simples - des expressions mathématiques telles que, par exemple, x
2 + 1.
Supposons, par exemple, que votre champ final contienne les nombres 1, 2 et 3. Ces nombres seront les coefficients du polynôme dans ce champ fini, et le polynôme «simple» sera celui qui ne peut pas être factorisé en facteurs polynomiaux. Par conséquent, x
2 + x + 2 sera simple, car il ne peut pas être factorisé, mais x
2 - 1 ne le sera pas: c'est le produit de (x + 1) et (x - 1).
Ayant défini des polynômes simples, il est naturel de poser une question sur les polynômes jumeaux simples - des paires de polynômes qui sont simples et diffèrent par une valeur fixe. Par exemple, le polynôme x
2 + x + 2 est simple, comme x
2 + 2x + 2. Ils diffèrent par x.
L'hypothèse de polynômes jumeaux simples pour les champs finis indique l'existence d'un nombre infiniment grand de paires de polynômes jumeaux simples qui diffèrent non seulement par x, mais par n'importe quelle valeur.
Coupes soignées
Les concepts de champs finis et de polynômes simples peuvent sembler farfelus et inutiles pour étudier les propriétés des nombres. Mais ils ressemblent à un simulateur d'ouragan - un univers en soi, donnant des idées sur les phénomènes se déroulant dans un grand monde.
«Il existe une ancienne analogie entre les entiers et les polynômes, qui nous permet de convertir des problèmes potentiellement extrêmement complexes liés aux entiers en problèmes liés aux polynômes, qui sont également potentiellement complexes, mais peuvent être plus faciles à résoudre», a déclaré Shusterman.
Les champs finis sont devenus célèbres en 1940 quand
Andre Weil a développé la manière exacte de traduire l'arithmétique des systèmes de petits nombres en l'arithmétique des entiers. Weil a utilisé cette connexion avec des résultats étonnants. Il a
montré , peut-être, le problème le plus important en mathématiques - l'hypothèse de Riemann - pour le cas d'un ensemble de courbes sur des champs finis (ce problème est connu sous le nom d'hypothèse géométrique de Riemann). Cette preuve, ainsi qu'un ensemble d'
hypothèses supplémentaires de
Weyl, ont fait des champs finis un paysage riche pour les découvertes mathématiques.
L'idée clé de Weil était que dans les domaines finis, les techniques géométriques peuvent être utilisées pour trouver des réponses aux questions sur les nombres. «C'est une caractéristique des champs finis. De nombreuses tâches que vous souhaitez résoudre peuvent être reformulées géométriquement », a déclaré Shusterman.
Pour comprendre comment la géométrie apparaît dans un tel environnement, imaginez chaque polynôme comme un point dans l'espace. Les coefficients d'un polynôme servent de coordonnées déterminant son emplacement. Revenant à notre champ final de 1, 2 et 3, le polynôme 2x + 3 est situé au point (2, 3) de l'espace bidimensionnel.
Mais même dans l'espace fini le plus simple, il existe un nombre infini de polynômes. Des polynômes plus complexes peuvent être créés en augmentant l'exposant du plus grand exposant, ou le degré d'expression. Dans notre cas, le polynôme x
2 - 3x - 1 sera représenté par un point dans l'espace tridimensionnel. Et le polynôme 3x
7 + 2x
6 + 2x
5 - 2x
4 - 3x
3 + x
2 - 2x + 3 sera représenté par un point dans l'espace à huit dimensions.
Dans le nouvel ouvrage, cet espace géométrique représente tous les polynômes d'un degré donné pour un champ fini donné. La question devient la suivante: existe-t-il un moyen d'isoler tous les points dénotant des polynômes simples?
La stratégie de Savin et Shusterman est de diviser l'espace en deux parties. Dans une partie, il y aura tous les points correspondant aux polynômes avec un nombre pair de facteurs. Dans l'autre, tous les points correspondant à des polynômes avec un nombre impair de facteurs.
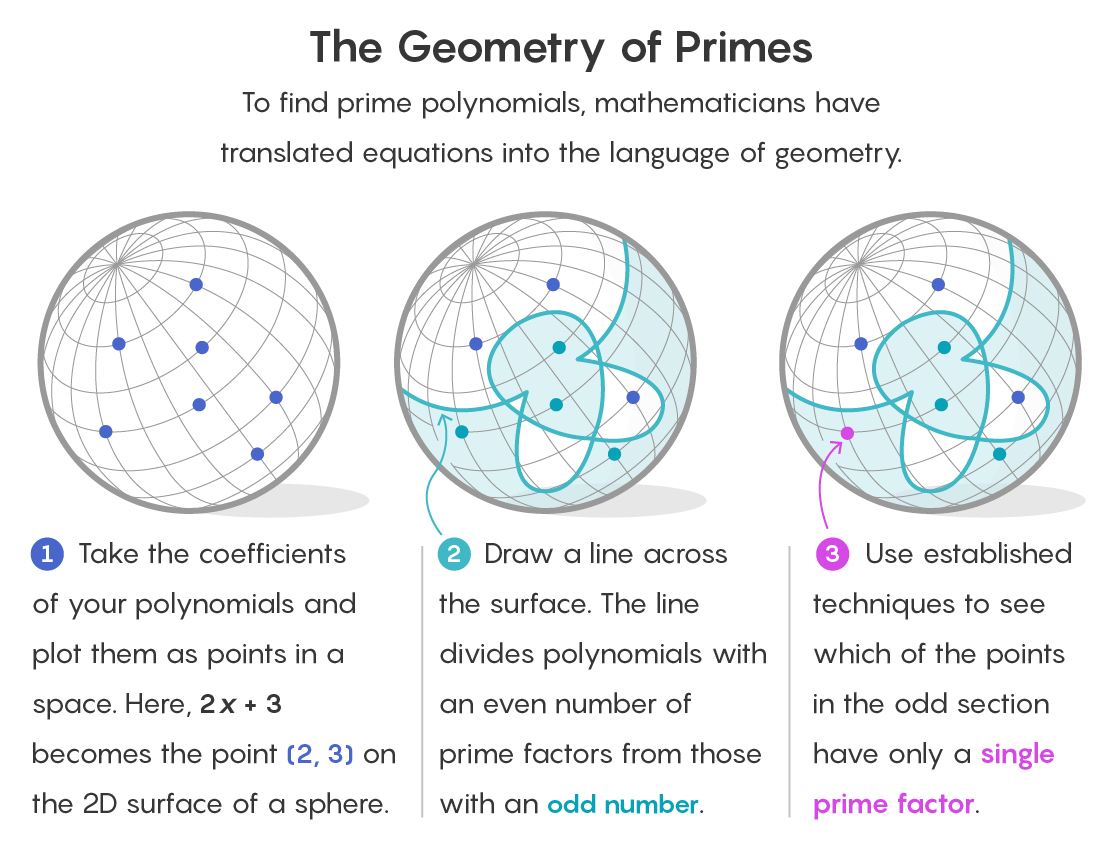
Cela simplifie déjà la tâche. L'hypothèse de simples polynômes jumeaux pour les champs finis ne s'applique qu'aux polynômes à un facteur (tout comme un nombre premier a un facteur, c'est lui-même). Et comme le nombre 1 est impair, une partie de l'espace contenant des polynômes avec un nombre pair de facteurs peut être immédiatement éliminée.
L'astuce consiste à utiliser la division. Dans le cas d'un objet bidimensionnel, par exemple, la surface d'une sphère, il est coupé en deux par une courbe unidimensionnelle - tout comme l'équateur coupe la surface de la Terre. Un objet avec un grand nombre de dimensions peut toujours être coupé avec un objet avec le nombre de dimensions moins un.
Mais ces formes de dimensions moindres, divisant l'espace des polynômes, ne sont pas du tout aussi élégantes que l'équateur. Ils sont dessinés selon une formule mathématique appelée
la fonction Mobius . En entrée, il prend un polynôme et en sortie, il donne 1 si le polynôme a un nombre pair de facteurs premiers, -1 s'il a un nombre impair et 0 s'il est factorisé (puisque 16 peut être divisé par 2 × 2 × 2 × 2).
Les courbes dessinées par la fonction Mobius se plient et se tordent comme des fous, se croisant en de nombreux endroits. Ces lieux, appelés singularités, sont particulièrement difficiles à analyser (ils correspondent à des polynômes décomposés en plusieurs facteurs premiers identiques).
L'innovation fondamentale de Savin et Shusterman a été de trouver le moyen exact de couper des boucles avec moins de mesures en segments plus courts. Ces segments étaient plus faciles à apprendre que l'ensemble de la boucle.
Après avoir compilé un catalogue de polynômes avec un nombre impair de facteurs premiers - et c'était le plus difficile - Savin et Shusterman ont été confrontés à la tâche de déterminer lesquels sont simples et lesquels sont jumeaux. Pour ce faire, ils ont appliqué plusieurs formules utilisées par les mathématiciens pour étudier les nombres premiers parmi les nombres ordinaires.
Savin et Shusterman ont utilisé leur technique pour prouver deux points importants concernant les polynômes simples dans certains domaines finis.
Premièrement, l'hypothèse des nombres premiers jumeaux dans les champs finis est vraie: il existe une infinité de paires de polynômes jumeaux qui diffèrent par une valeur donnée.
Deuxièmement, et plus important encore, ce travail fournit un décompte précis du nombre de polynômes jumeaux simples qui peuvent être trouvés parmi les polynômes d'un certain ordre. Cela revient à savoir combien de nombres premiers jumeaux se trouvent à l'intérieur d'un intervalle suffisamment long sur une droite numérique - et ce n'est que le rêve des mathématiciens.
"C'est le premier travail qui donne une analogie quantitative de ce qui devrait être vrai pour les nombres entiers, et c'est un résultat vraiment exceptionnel", a déclaré Ziv Rudnik de l'Université de Tel Aviv. "Jusqu'à présent, rien de tel n'est arrivé."
La preuve de Savin et Schusterman montre comment, près de 80 ans après qu'André Weil a prouvé l'hypothèse de Riemann pour les courbes sur des champs finis, les mathématiciens avancent obstinément dans cette direction. Maintenant, les mathématiciens qui traitent de l'hypothèse du premier principe se tourneront vers le travail de Savin et Shusterman, et peut-être cela leur donnera une source profonde d'inspiration.