Quel est le prochain membre ...? - Nous recherchons une formule pour le nième terme de la séquence, générant des fonctions et Z-transformation

Vous pouvez télécharger le fichier avec le code et les données dans l'article d' origine sur mon blog

Wolfram Language possède quatre fonctionnalités complètement impressionnantes: FindSequenceFunction , RSolve , DifferenceRootReduce et FindFormula . Dans cet article, nous allons discuter de leurs capacités et parler des fonctions qui leur sont étroitement liées - pour rechercher des FindLinearRecurrence récursion linéaire FindLinearRecurrence (coefficients d'une équation de récurrence linéaire) qui génèrent les fonctions GeneratingFunction et ZTransform Z-transform.

La première fonction , FindSequenceFunction, recherche une expression pour son nième membre par une séquence de nombres sans rien exiger de plus.

 Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n] 

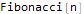
 FindSequenceFunction[ {-2, 4Sqrt[Pi], -16, 16Sqrt[Pi], -128/3, 32Sqrt[Pi], -1024/15, 128Sqrt[Pi]/3, -8192/105, 128Sqrt[Pi]/3}, n] 

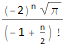La deuxième fonction , RSolve, résout des équations de récurrence de différents types. Les éléments peuvent ressembler $$$a [f [n]]$, $$$a [f [f [n]]]$, $$$a [f [f [\ text {...} f [n] \ text {...}]]]$, où f a la forme: n + A (équations de différence arithmétique), B * n - équations de différence géométrique ou q), B * n + a (équations de différence fonctionnelle arithmétique et géométrique), B * n ^ d (fonction géométrique de puissance équations aux différences), (A * n + B) / (C * n + D) (équations aux différences fonctionnelles fractionnaires linéaires).

 RSolve[ { a[n + 3]==2 * a[n], a[1]==α, a[2]==β, a[3]==γ }, a, n ] 

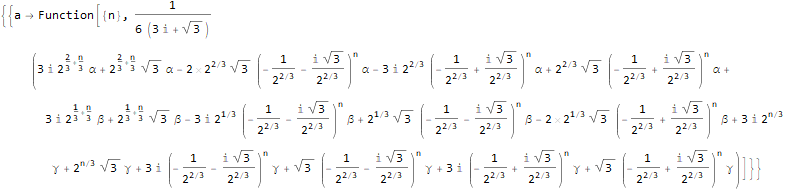
 RSolve[ { v[n]==(2 * Pi * v[n - 2]) / n, v[2]==Pi, v[3]==(4 * Pi) / 3 }, v @ n, n ] 

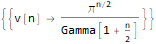La troisième fonction - DifferenceRootReduce - recherche une relation de récurrence pour une séquence de nombres, dont le nième membre a une forme donnée.

 DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1], n ] 

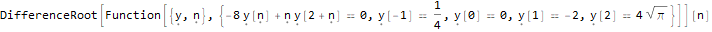
 RSolve[ { (-8 * y[n]) + n * y[2 + n]==0, y[-1]==1/4, y[0]==0, y[1]==-2, y[2]==4Sqrt[Pi] }, y, n ] 

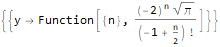
Cette fonction peut faire beaucoup plus, disons, vérifier les identités par rapport aux séquences, par exemple:

 DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n] 

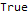
Ici LucasL est une séquence de nombres de Luc (il s'agit, en fait, d'une séquence de Fibonacci, seuls les premiers membres ne sont pas 1, 1, mais 1, 3.

 Hold @ DifferenceRootReduce @ LucasL @ n 

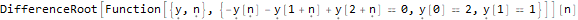
 DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]] 

Comment trouver une formule de récurrence pour une séquence?

La méthode de recherche d'un membre commun d'une séquence est souvent basée sur la nécessité de sélectionner une équation de récurrence.

Cela peut fonctionner quelque chose comme ceci: recherchons le nième terme dans le formulaire $$$f [n] = \ sum_ {i = 1} ^ ka [i] f [n-i]$. Ayons les premiers membres de la séquence:

 sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461} 

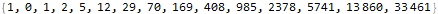
Essayons de trouver une expression pour le nième terme sous la forme $$$f [n] = \ sum_ {i = 1} ^ 1a [i] f [n-i] = a [1] f [n-1]$:

 seauenseEq1 = MovingMap[ Function[ Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1] ], sequence, 1 ] 

 Hold @ Solve @ seauenseEq1 

Comme vous pouvez le voir, il n'y a pas de solutions.

Essayons de rechercher maintenant dans le formulaire $$$f [n] = \ sum_ {i = 1} ^ 2a [i] f [n-i] = a [1] f [n-1] + a [2] f [n-2]$:

 seauenseEq2 = MovingMap[ Function[ Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1] ], sequence, 2 ] 

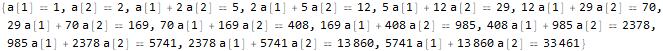
 Hold @ Solve @ seauenseEq2 

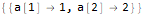
Comme nous le voyons, il s'est avéré. Par conséquent, le nième terme a la forme: $$$f [n] = f [n-1] + 2f [n-2]$.

En fait, il existe une fonction FindLinearRecurrence intégrée qui vous permet de trouver une récursivité linéaire, semblable à la façon dont nous venons de le faire:

 Hold @ FindLinearRecurrence @ sequence 

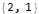
En utilisant la fonction LinearRecurrence , LinearRecurrence pouvez étendre la séquence:

 LinearRecurrence[{2, 1}, sequence[[1;;2]], 50] 

Ou tout combiner en une seule ligne en construisant une fonction qui: étend la séquence, produit une équation de différence et trouve une formule générale pour le nième terme:

 sequenseExtension[list_, n_] := Module[ {lr, eq}, lr = FindLinearRecurrence @ list; eq = Flatten[ { a[k]==Total[ Table[ a[k + -i] * Part[lr, i], {i, 1, Length @ lr} ] ], Table[a[i], list[[i]]], {i, 1, Length @ lr}] } ]; <| "" -> eq, "" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]], "" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n] |> ]; 

 Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20] 

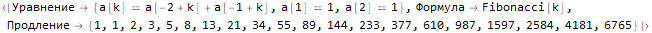
 Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20] 

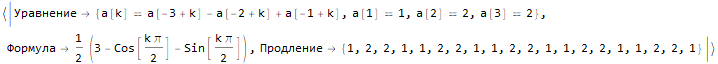
 Hold @ sequenseExtension[ {1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4}, 25 ] 

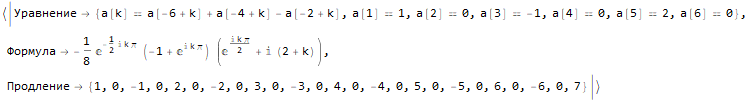
Comment trouver la formule du nième membre d'une séquence?

Conversion Z

La transformation en Z consiste à calculer une série de la forme $$$\ sum_ {n = 0} ^ {\ infty} f (n) z ^ {- n}$de la fonction discrète $$$f (n)$. Cette transformation nous permet de réduire l'équation de récurrence pour définir la séquence à l'équation pour l'image de la fonction $$$f (n)$, qui est similaire à la transformée de Laplace, qui réduit les équations différentielles aux algébriques.

Voici comment cela fonctionne:

 Grid[ Transpose[ Function[ { #, Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]] } ][ { f[n - 2], f[n - 1], f @ n, f[n + 1], f[n + 2] } ] ], Background -> White, Dividers -> All ] 

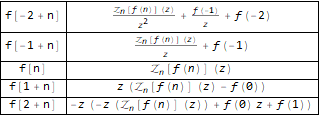
Regardons un exemple, disons, prenons la séquence bien connue de Fibonacci:

 fibonacciEq = f[n]==f[n - 1] + f[n - 2]; initialConditions = {f[1] -> 1, f[2] -> 1}; 

Il est clair qu'il doit être réécrit sous la forme, comme illustré ci-dessous, de sorte que les constructions comme $$$f (-1)$après avoir appliqué la transformée en Z.

 fibonacciEq = f[n + 2]==f[n + 1] + f[n]; initialConditions = {f[0] -> 1, f[1] -> 1}; 

Nous réalisons la transformation Z:

 fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]] 

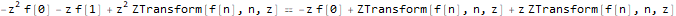
Nous résolvons l'équation de l'image de la fonction f - ZTransform [f [n], n, z]:

 fZTransformed = ReplaceAll[ ZTransform[f @ n, n, z], Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1] ] 

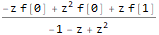
Nous effectuons la transformation Z inverse, en remplaçant les conditions initiales en même temps (nous remplaçons n par n-1 dans l'expression finale afin que notre séquence ait l'indexation correcte (à partir du premier, pas du terme zéro):

 ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n], n -> (n - 1) ] 

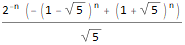
Naturellement, cela peut être automatisé en créant votre propre homologue RSolve:

 myRSolve[eq_, initials_, f_, n_] := Module[ {z, initialsInner, eqZTransformed, fZTransformed}, initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]]; eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]]; fZTransformed = ReplaceAll[ZTransform[f @ n, n, z], Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1] ]; FullSimplify[ InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1) ] ]; 

 myRSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]) }, {f[1] -> 20, f[2] -> 0}, f, n ] 

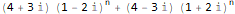
 RSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]), f[1]==20, f[2]==0 }, f, n ] 

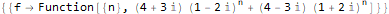
Mais, bien sûr, RSolve contient beaucoup plus de possibilités pour résoudre une grande variété d'équations discrètes, sur lesquelles nous n'insisterons pas plus en détail:

 RSolve[a[n]==(n * a[n]) + n, a, n], RSolve[ { a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4, a[0]==0 }, a, n ], RSolve[ y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2, y, n ] 

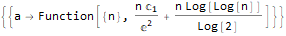
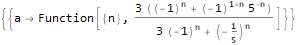
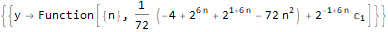
Génération de fonctions

Génération d'une fonction de séquence $$$a (n)$c'est une telle fonction $$$G (x)$, dont l'expansion dans la série Taylor (ou, plus largement, Laurent) a la forme - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} a (n) x ^ n$. En d'autres termes, les coefficients de puissances de x dans l'expansion de la fonction dans une série déterminent notre séquence.

Fonction Say $$$G (x) = \ frac {1} {1-x}$est une fonction génératrice de la séquence 1, 1, 1, 1, ...:

 Series[1 / (1 + -x), {x, 0, 10}] 

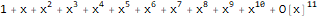
Une fonction $$$G (x) = \ frac {1} {1-x-x ^ 2}$est une fonction génératrice de la séquence de Fibonacci 1, 1, 2, 3, 5, 8, 13, ...:

 Series[(1 * 1) + (-x) + -(x * 2), {x, 0, 10} ] 

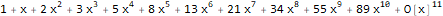
Il y a aussi une sorte de fonction génératrice - une fonction génératrice exponentielle, qui pour la séquence $$$a (n)$a la forme - $$$G (x) = \ sum_ {i = 0} ^ {\ infty} \ frac {a (n)} {n!} X ^ n$.

Disons que pour les séquences 1, 1, 1, 1 ... et 1, 1, 2, 3, 5, 8, 13, ... les fonctions de génération exponentielle sont les suivantes - $$$e ^ x$et $$$\ frac {1} {\ sqrt {5}} e ^ {- \ frac {2x} {1+ \ sqrt {5}}} \ left (e ^ {\ sqrt {5} x} -1 \ right)$:

 ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

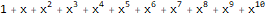
 ReplaceAll[ Normal[ FullSimplify[ Series[ Plus[E, (-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5 ], {x, 0, 10} ] ] ], Power[x, n_] :> ((x ^ n) * Factorial[n]) ] 

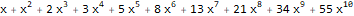
La fonction de production dans Wolfram Language peut être trouvée par deux fonctions - GeneratingFunction et FindGeneratingFunction (exponentielle avec ExponentialGeneratingFunction ):

 GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}] 

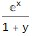
 TraditionalForm[ FullSimplify[ ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x] ] ] 

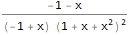
Il existe de nombreuses méthodes pour trouver un membre commun d'une séquence à l'aide de fonctions de génération. Nous ne nous attarderons pas sur cela en détail, disons, juste une bonne théorie est sur le site genfunc.ru .

L'une des méthodes est similaire à la transformation Z:

 generatingFEq = ReplaceAll[ f[n + 2]==f[n + 1] + f[n], pattern:f[__] :> GeneratingFunction[pattern, n, z] ], generatingF = ReplaceAll[ GeneratingFunction[f @ n, n, z], Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1] ], nthTerm = SeriesCoefficient[generatingF, {z, 0, n}], FullSimplify[ ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}], n -> (n - 1) ], GreaterEqual[n, 1] ] 

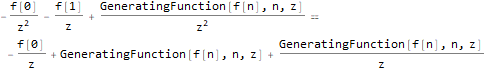
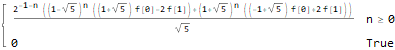
OEIS - Encyclopédie de séquences entières en ligne et intégration avec Wolfram Language

Une collection absolument époustouflante de séquences de nombres est disponible sur Internet - OEIS (On-Line Encyclopedia of Integer Sequences) . Il a été créé par Neil Sloan au cours de sa carrière de chercheur chez AT&T Labs. OEIS stocke des informations sur les séquences entières d'intérêt pour les amateurs et les professionnels en mathématiques, combinatoire, théorie des nombres, théorie des jeux, physique, chimie, biologie, informatique. Actuellement, 329085 séquences y sont collectées. Un enregistrement dans OEIS comprend les premiers éléments d'une séquence, des mots clés, une description mathématique, le nom des auteurs, des liens avec la littérature; il y a la possibilité de tracer ou de jouer une représentation musicale de la séquence. Une recherche dans la base de données peut être effectuée par mots-clés et par sous-séquence.

Récemment, l'intégration avec cette base de données est apparue à l'intérieur du Wolfram Language (lors de son utilisation, il est important de comprendre qu'il s'agit d'un développement utilisateur - récemment, vous pouvez télécharger votre code dans le Wolfram Function Repository ). Entrez simplement le numéro de la séquence qui vous intéresse ou une liste de numéros.

 OEISSequenceData = ResourceFunction @ "OEISSequenceData"; OEISSequence = ResourceFunction @ "OEISSequence"; 

ResourceFunction ["OEISSequence"] - renvoie simplement les premiers membres de la séquence:

 Hold @ OEISSequence @ "A666" 

ResourceFunction ["OEISSequenceData"] - émet un ensemble de données avec toutes les informations de la base de données:

 sequenceData[666] = OEISSequenceData[666, "Dataset"] 

Disons que vous pouvez «retirer» le code Wolfram Language:

 Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"] 

Ou un ensemble de séquences sélectionnées au hasard avec des informations qui les intéressent:

 randomSequences = Dataset @ Map[ Normal, OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"] ]; 

 Function[ Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White] ][ Grid[ Join[ { Map[Style[#, Bold, 18]&, {"", "", "", " ", "  "} ] }, Map[ Function[ Map[ Function[ TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"] ], { Style[Part[#, 1], 16], Row[Part[#, 4], "\n"], Row[Part[#, 3], "\n"], Style[Row[Part[#, 2], "; "], 10], ListLinePlot[Part[#, 2], ImageSize -> Full] } ] ], Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}] ] ], Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}}, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], ItemSize -> {{15, 25, 10, 15, 15}, Automatic}, Alignment -> {Left, Center}, Background -> {None, {LightOrange, White}} ] ] 

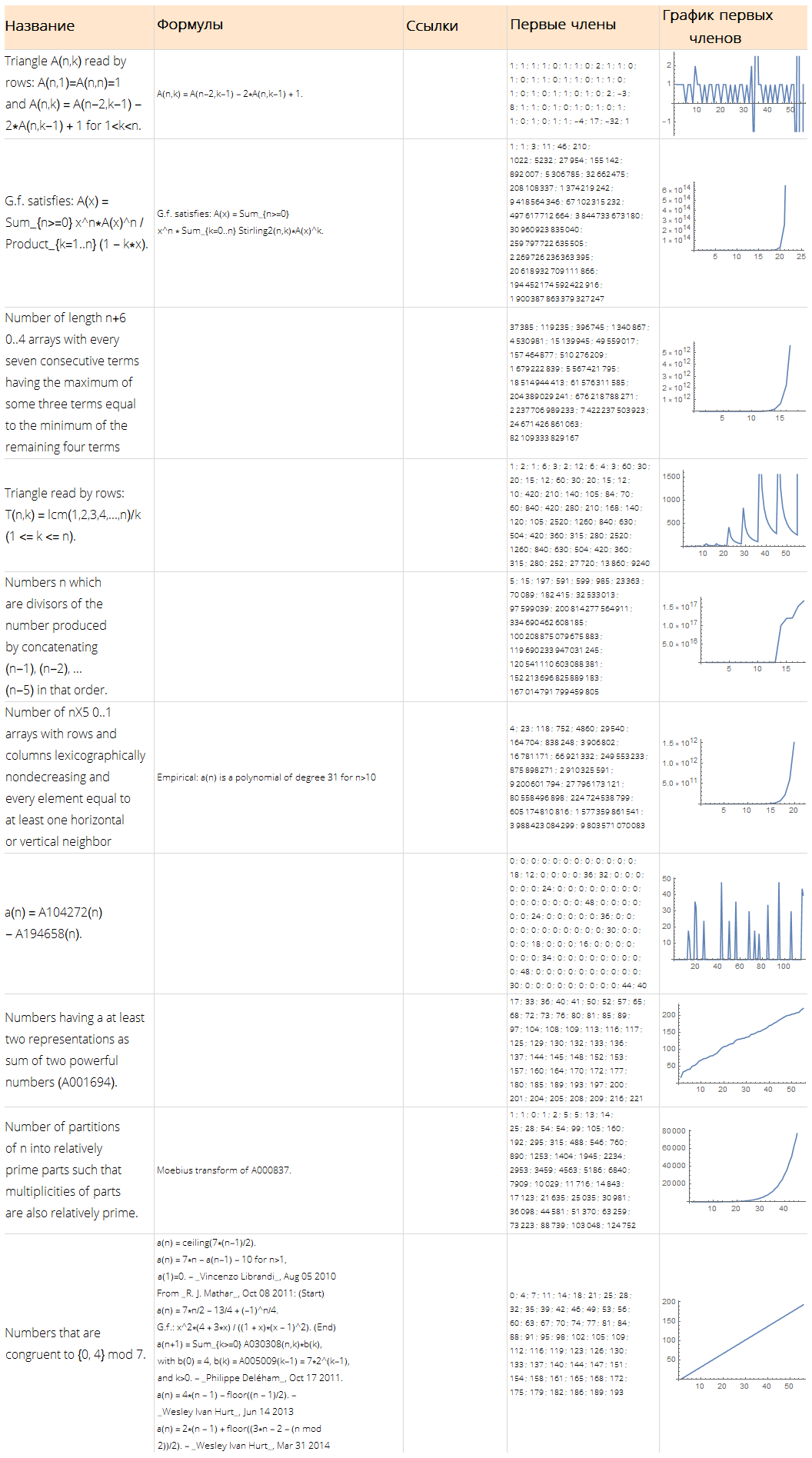
Rechercher une formule potentielle

Enfin, je voudrais mentionner la fonction FindFormula , qui, sur la base d'un ensemble de nombres donné, construit une formule qui peut les décrire. Nous pouvons accepter les dépendances, vous pouvez choisir beaucoup de différentes classes de fonctions.

 data = Table[ { x, Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]] }, {x, RandomReal[{-10, 10}, 1000]} ]; ListPlot[data, Background -> White, ImageSize -> 600] 

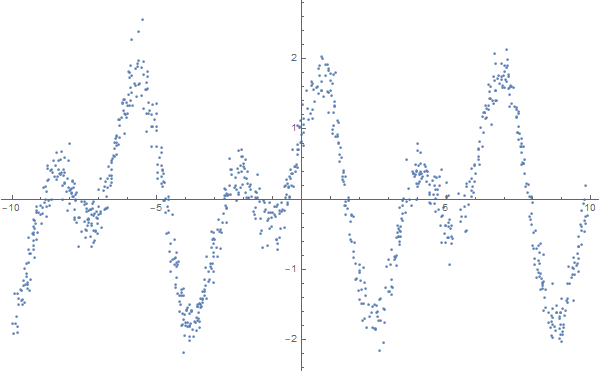
 formulas = FindFormula[data, x] 

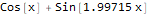
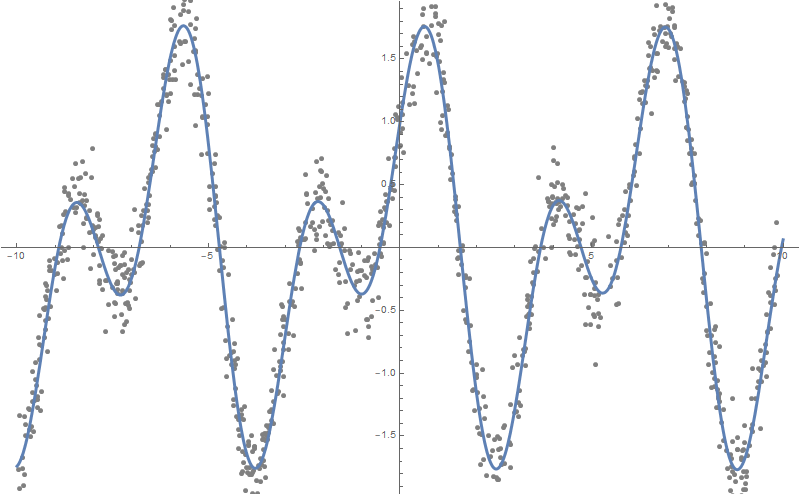
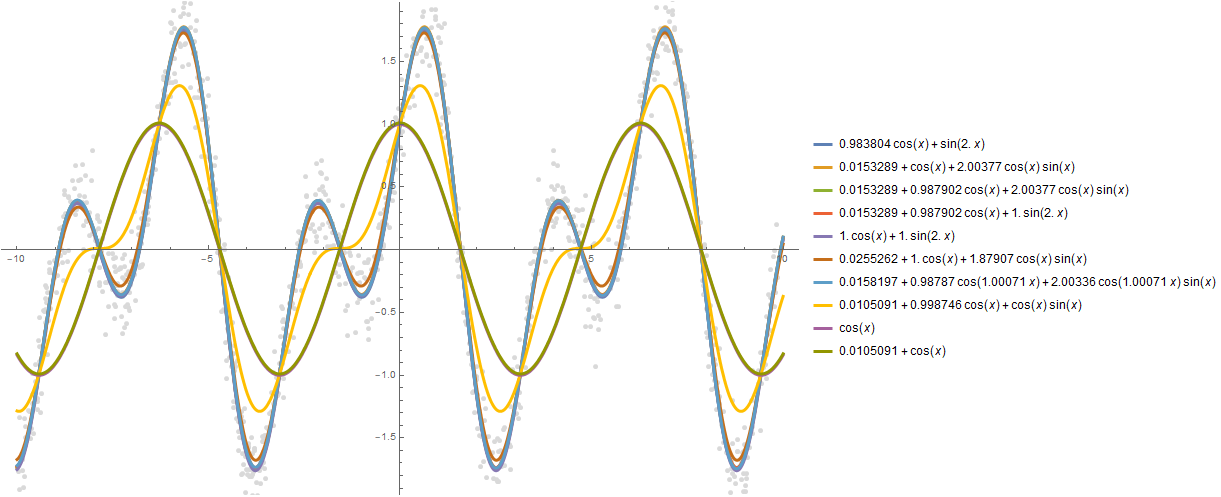
Comme vous pouvez le voir, Wolfram Language a choisi une fonction très proche de celle sur la base de laquelle des données "bruyantes" ont été construites, à savoir - Sin [2x] + Cos [x]:

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], Gray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

Vous pouvez créer plus de dépendances, disons 10:

 formulas = FindFormula[data, x, 10] 

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], LightGray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ] 

Il convient de noter qu'il existe une fonction similaire dans la fonctionnalité qui recherche une distribution de probabilité - FindDistribution .

Pour la coopération - écrivez un message personnel sur Habré ou dans mon groupe VKontakte .
Chaîne YouTube - webinaires et vidéos de formation.
Inscription aux nouveaux cours . Cours en ligne prêt.