La théorie des catégories permet aux mathématiques d'abandonner les égalités

Deux œuvres monumentales ont convaincu de nombreux mathématiciens d'abandonner le signe égal. Leur objectif est de reconstruire les fondements de la discipline à l'aide d'une relation plus faible - «l'équivalence». Et ce processus ne se déroule pas toujours sans heurts.

Le signe égal est la pierre angulaire des mathématiques. Il semble faire une déclaration fondamentale et cohérente: ces deux entités sont exactement les mêmes.

Cependant, le cercle des mathématiciens s'agrandit, se référant au signe égal, à l'erreur initiale des mathématiques. Ils considèrent qu'il s'agit d'un gloss externe, cachant les complexités importantes de la relation entre les quantités - complexités qui peuvent ouvrir des solutions à un grand nombre de problèmes. Ils veulent réformer les mathématiques en utilisant un langage d'équivalence plus lâche.

«Nous avons engendré cette idée d'égalité», a déclaré Jonathan Campbell de l'Université Duke. "Et il aurait dû y avoir une équivalence à sa place."

La figure la plus importante de cette communauté est Jacob Lurie . En juillet, Lurie , 41 ans, a démissionné de son emploi à plein temps à Harvard pour un poste de professeur au Princeton Institute for Advanced Studies, où certains des plus grands mathématiciens du monde travaillaient.

Des idées d'une telle ampleur que celle de Lurie se retrouvent rarement dans aucun domaine. Dans ses livres couvrant des milliers de pages pleines de détails techniques, il a créé une manière étonnamment différente de la façon habituelle de comprendre les concepts les plus élémentaires des mathématiques, allant au-delà du signe égal. «Je pense qu'il lui a semblé que c'était la bonne façon de penser les mathématiques», a déclaré Michael Hopkins , mathématicien à Harvard et directeur des études supérieures.

Il a publié son premier livre, The Theory of Higher Topos , en 2009. Un volume de 944 pages sert d'instruction pour interpréter les domaines reconnus des mathématiques dans le nouveau langage des «catégories de l'infini». Au cours des années suivantes, les idées de Lurie ont pénétré un large éventail de disciplines mathématiques. De nombreux mathématiciens les considèrent comme indispensables pour l'avenir de ce domaine. "Personne ne sera plus le même après avoir étudié les catégories de l'infini", a déclaré John Francis de Northwestern University,


Jacob Lurie

Cependant, la propagation des catégories de l'infini a révélé tous les problèmes qu'un domaine respecté des mathématiques traverse, essayant d'absorber de nouvelles idées audacieuses - en particulier une idée qui remet en question son concept le plus important. "Il existe un certain niveau de conservatisme dans la communauté mathématique", a déclaré Clark Barwick de l'Université d'Edimbourg. "Je ne pense pas qu’on puisse attendre d’un groupe de mathématiciens d’accepter rapidement un outil sans raisons convaincantes."

Bien que de nombreux mathématiciens aient accepté les catégories de l'infini, peu ont lu l'intégralité des textes longs et extrêmement abstraits de Lurie. En conséquence, une partie du travail basé sur ses idées s'avère moins rigoureuse que ce qui est accepté en mathématiques.

«J'ai entendu des gens dire:« Lurie a quelque part », a déclaré Inna Zakharevich , mathématicienne à l'Université Cornell. - Et je dis: «Vraiment? Vous faites référence à 8 000 pages de texte. » Ce n'est pas une référence, c'est un appel à l'autorité. »

Les mathématiciens tentent toujours de réaliser l’ampleur des idées de Lurie et la manière unique de les présenter. Ils extraient l'essence de sa présentation des catégories de l'infini et la présentent dans un nouveau package pour que plus de mathématiciens puissent l'utiliser. Dans un sens, ils exercent la direction nécessaire, qui est obligée de suivre toute révolution, traduisant le texte révolutionnaire dans le code de lois quotidien. Ainsi, ils créent l'avenir des mathématiciens, basé non pas sur l'égalité, mais sur l'équivalence.

Tours d'équivalence sans fin

L'égalité mathématique semble la moins controversée de toutes les idées. Deux perles plus une perle équivalent à trois perles. De quoi d'autre pouvons-nous parler? Cependant, les idées les plus simples peuvent être les plus trompeuses.

Depuis la fin du XIXe siècle, les fondements des mathématiques se sont construits sur des ensembles d'objets appelés ensembles. La théorie des ensembles définit les règles, ou axiome, pour la création et la gestion de ces ensembles. L'un de ces axiomes, par exemple, prétend que vous pouvez ajouter un ensemble d'un élément à un ensemble de deux éléments et obtenir un nouvel ensemble de trois éléments: 2 + 1 = 3.

La manière formelle de démontrer l'égalité de deux quantités consiste à faire correspondre les paires. Faites correspondre une perle à droite du signe égal avec une perle à gauche. Après toutes les comparaisons, il ne restera plus de perles supplémentaires.

La théorie des ensembles reconnaît que deux ensembles de trois objets chacun peuvent être précisément associés l'un à l'autre, mais ne signifie pas toutes les différentes manières possibles d'une telle comparaison. Le premier cordon à droite peut ramasser une paire sous la forme du premier cordon à gauche, ou faire correspondre le premier à droite avec le second à gauche, et ainsi de suite (il peut y avoir six de ces paires). Dire que deux plus un est égal à trois, et terminer sur cela signifie ne pas voir toutes les façons possibles de les égaliser. «Le problème est qu'il existe de nombreuses façons de s'associer», explique Campbell. "Et nous les oublions quand nous disons égaux."



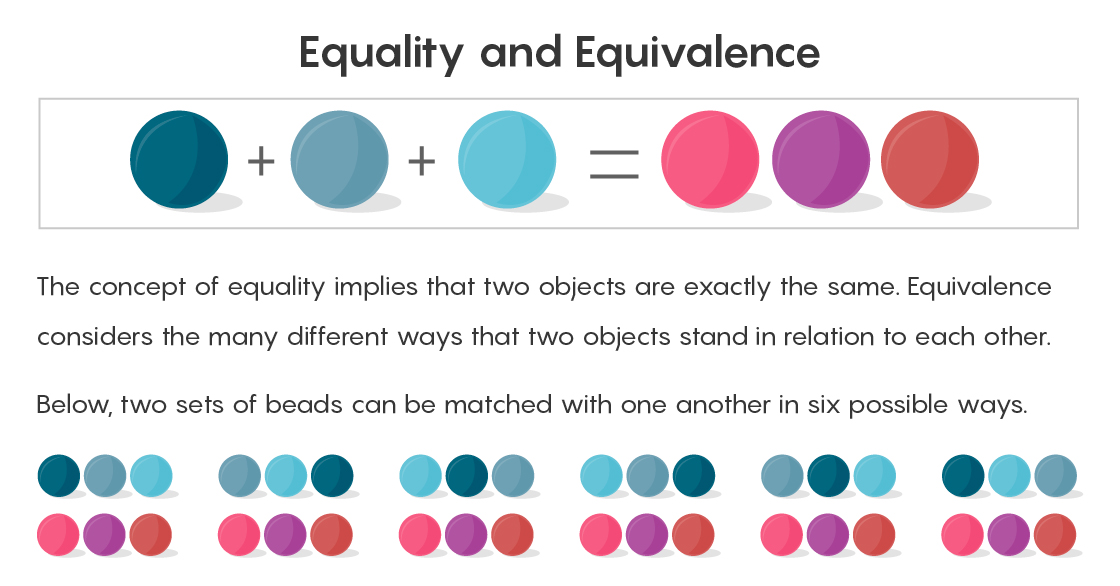
C'est là que l'équivalence entre en jeu. Si l'égalité est une relation claire - deux choses sont égales ou non - l'équivalence peut être différente.

Lorsque vous faites correspondre précisément chaque élément d'un ensemble à chaque élément d'un autre, vous obtenez une forte équivalence. Mais, par exemple, dans un domaine des mathématiques comme l' homotopie , deux formes (ou figures géométriques) sont équivalentes si l'une peut être transformée en une autre par étirement ou compression sans se casser.

Du point de vue de la théorie de l'homotopie, un disque plat et un point dans l'espace sont équivalents - le disque peut être compressé en un point. Cependant, vous ne pouvez pas faire correspondre les points d'un disque avec les points d'un point. En effet, le disque de points a un nombre infini, et un point n'est qu'un point.



Depuis le milieu du XXe siècle, les mathématiciens tentent de développer une alternative à la théorie des ensembles dans laquelle les mathématiques seraient plus faciles à gérer en termes d'équivalence. En 1945, les mathématiciens Samuel Eileberg et Saunders MacLane ont introduit un nouvel objet fondamental avec une équivalence intégrée. Ils l'ont appelé une catégorie.

Une catégorie peut être remplie de n'importe quoi. Vous pouvez prendre la catégorie des mammifères, qui comprendra toutes les créatures velues à sang chaud qui produisent du lait. Ou vous pouvez créer des catégories d'objets mathématiques: ensembles, formes géométriques ou systèmes numériques.

Une catégorie est un ensemble avec des métadonnées supplémentaires: une description de toutes les façons de faire correspondre un objet à un autre, qui comprend une description de toutes les fonctionnalités par lesquelles deux objets peuvent être considérés comme équivalents. Les catégories peuvent également être imaginées comme des objets géométriques dans lesquels chaque élément de la catégorie est représenté par un point.

Imaginez, par exemple, la surface d'une balle. Chaque point sur cette surface peut indiquer son type de triangles. Les chemins entre les points expriment une relation d'équivalence entre les objets. Du point de vue de la théorie des catégories, nous oublions la manière spécifique de décrire un objet et nous concentrons plutôt sur la place qu'il occupe par rapport à tous les autres objets de ce type.


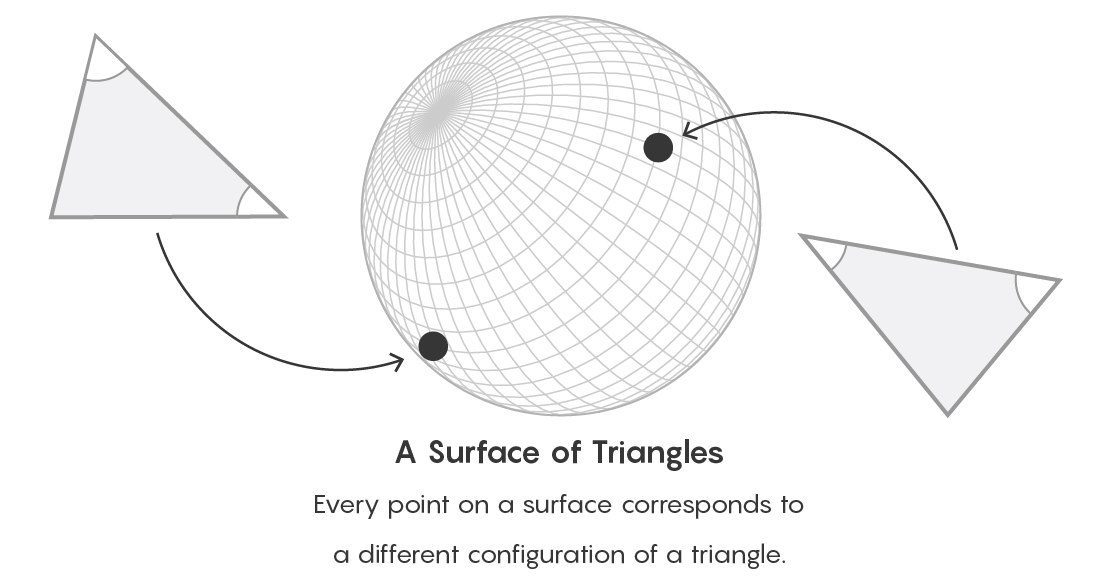Chaque point de la surface correspond à un type particulier de triangles.

"Nous traitons beaucoup de choses comme des choses, bien qu'en réalité ce soient des relations entre les choses", a expliqué Zakharevich. - L'expression «mon mari» signifie quelque chose que nous considérons comme un objet, mais vous pouvez le considérer comme une relation. Une certaine partie est déterminée par la relation avec moi. »

La version de catégorie d'Eilenberg et MacLane était bien adaptée pour travailler avec de fortes options d'équivalence. Mais dans la seconde moitié du 20e siècle, les mathématiciens ont de plus en plus utilisé des formes d'équivalence plus faibles, comme l'homotopie. «Les mathématiques deviennent de plus en plus subtiles et nous avons inévitablement le désir d'avoir des idées plus subtiles sur les choses ordinaires», a déclaré Emily Riel, mathématicienne à l'Université Johns Hopkins. Dans ces versions plus fines de l'équivalence, la quantité d'informations sur la relation entre deux objets augmente fortement. Les catégories rudimentaires d'Eilenberg et de MacLane n'étaient pas destinées à cela.

Pour voir une augmentation de la quantité d'informations, souvenez-vous d'abord de notre sphère, désignant différents triangles. Deux triangles sont homotopiquement équivalents si l'un peut être transformé en un autre par étirement ou autre déformation. Deux points sur une surface sont homotopiquement équivalents s'il y a un chemin qui les relie. En étudiant les trajets homotopiques entre les points d'une surface, vous étudiez en fait les différentes façons dont les triangles désignés par ces points sont connectés les uns aux autres.



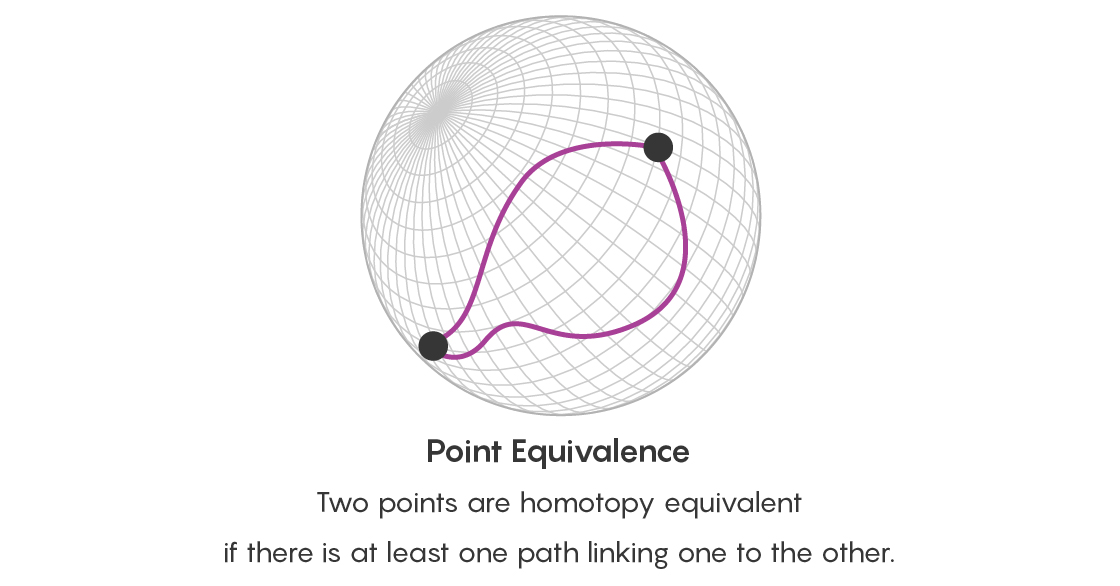
Cependant, il ne suffit pas de déclarer que deux points sont connectés de nombreuses manières équivalentes. Il faut aussi penser à l'équivalence de tous ces chemins. Par conséquent, en plus de la question de l'équivalence des points, vous posez maintenant la question de l'équivalence de deux chemins commençant et se terminant aux mêmes points - et y a-t-il un chemin reliant ces chemins. Ce chemin reliant les chemins prend la forme d'un disque dont les limites sont deux de ces chemins.



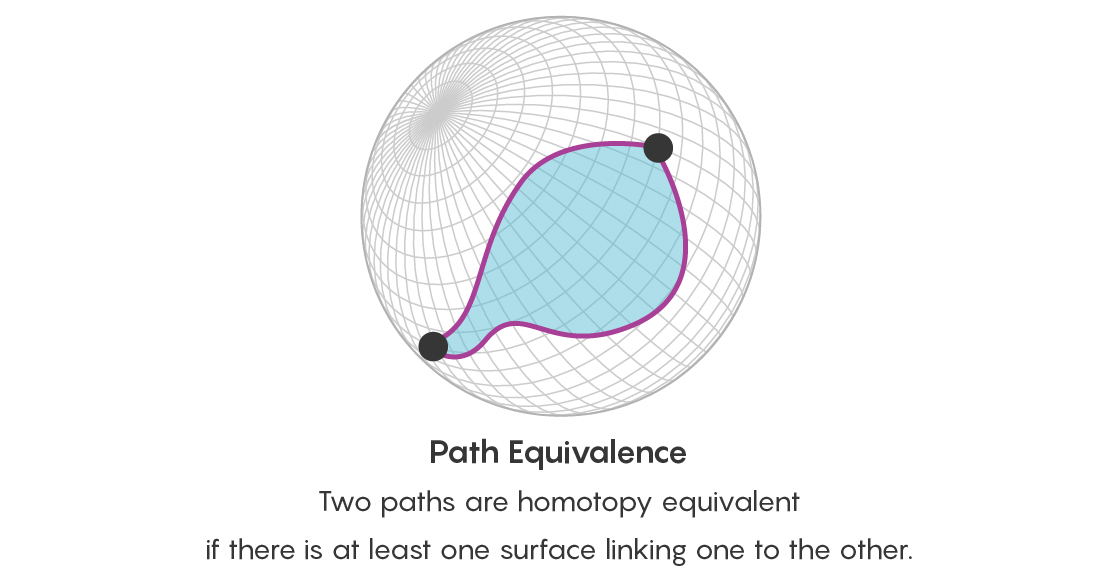
Vous pouvez développer cette idée davantage. Deux disques sont équivalents s'ils sont connectés par un chemin - et ce chemin prendra la forme d'un objet tridimensionnel. De tels objets tridimensionnels peuvent eux-mêmes être reliés par des chemins quadridimensionnels (le chemin entre deux objets a toujours une dimension de plus que les objets eux-mêmes).

En conséquence, vous construisez une tour sans fin d'équivalence entre équivalences. En discutant de l'ensemble de la doctrine, vous générez une vue générale de tous les objets que vous avez marqués de points sur la sphère.

"C'est juste une sphère, mais il s'avère que pour comprendre la forme d'une sphère, vous devez entrer dans l'infini d'une manière ou d'une autre", a déclaré David Ben-Zvi de l'Université du Texas à Austin.

Au cours des dernières décennies du XXe siècle, de nombreux mathématiciens ont travaillé sur la théorie des «catégories d'infinis» - sur ce qui est capable de suivre une tour infinie d'équivalences entre équivalences. Certains d’entre eux ont connu un grand succès. Mais un seul a atteint la fin.

Réécriture des mathématiques

Le premier travail de Jacob Lurie dans les catégories de l'infini n'a pas été très réussi. Le 5 juin 2003, le scientifique de 25 ans a publié un document de 60 pages intitulé " On the Topos of Infinity " sur le site des prépublications scientifiques arxiv.org. Là, il a commencé à faire des ébauches des règles par lesquelles les mathématiciens pouvaient travailler avec des catégories d'infini.

Tout le monde n'a pas accepté le premier travail de la même manière. Peu de temps après la lecture, Peter May , mathématicien à l'Université de Chicago, a écrit au superviseur de Lurie, Michael Hopkins, que bien que le travail de Lurie contienne des idées intéressantes, il semble inachevé et nécessite une approche plus disciplinée.

"J'ai expliqué nos commentaires à Mike, et il les a transmis à Jacob", a déclaré May.

On ne sait pas si Lurie a pris la lettre de May comme un défi, ou s'il avait déjà planifié sa prochaine étape (Lurie a rejeté de nombreuses demandes d'entretien). Il est clair qu'après avoir reçu des commentaires critiques, Lurie a atteint une période de productivité de plusieurs années, qui est devenue plus tard légendaire.

"Je ne peux pas entrer dans le cerveau de Jacob, et donc je ne sais pas exactement ce qu'il pensait alors", a déclaré May. "Mais il y a une énorme différence entre le projet que nous avons examiné et les versions finales, qui sont déjà à un niveau mathématique complètement différent."

En 2006, Lurie a publié sur arxiv.org un projet de «Théories des plus hauts topos». Dans cette œuvre monumentale, il a créé l'appareil nécessaire pour remplacer la théorie des ensembles par une nouvelle base mathématique basée sur les catégories de l'infini. "Il a créé littéralement des milliers de pages de cet appareil fondamental que nous utilisons tous maintenant", a déclaré Charles Rezk, mathématicien à l'Université de l'Illinois à Urbana-Champaign, qui a fait un travail important dès le début dans le développement des catégories infini. "Je ne peux pas imaginer comment il est possible de créer une œuvre comme" Theory of the Higher Topos "dans une vie - et il l'a créée en deux ou trois ans."

Puis en 2011, Lurie a donné un autre travail encore plus long. Il y réinvente l'algèbre.

L'algèbre nous donne un merveilleux ensemble de règles formelles pour manipuler des équations. Les mathématiciens utilisent constamment ces règles pour prouver les théorèmes. Cependant, l'algèbre fait de la gymnastique sur les barres fixes du signe égal. Supprimez ces barres, en les remplaçant par un concept d'équivalence plus éphémère, et certaines opérations deviendront très compliquées.

Prenez l'une des premières règles d'algèbre que les enfants apprennent à l'école: l'associativité. La somme ou le produit de trois nombres ou plus ne dépend pas de leur regroupement: 2 × (3 × 4) = (2 × 3) × 4.

Il est facile de prouver la propriété d'associativité pour une liste de trois nombres ou plus si vous travaillez avec l'égalité. C'est difficile lorsque vous travaillez même avec le concept de forte équivalence. Mais lorsque vous passez à des versions d'équivalence plus subtiles, avec leurs tours sans fin de chemins reliant les chemins, même une simple règle, similaire à l'associativité, se transforme en une forêt sombre.


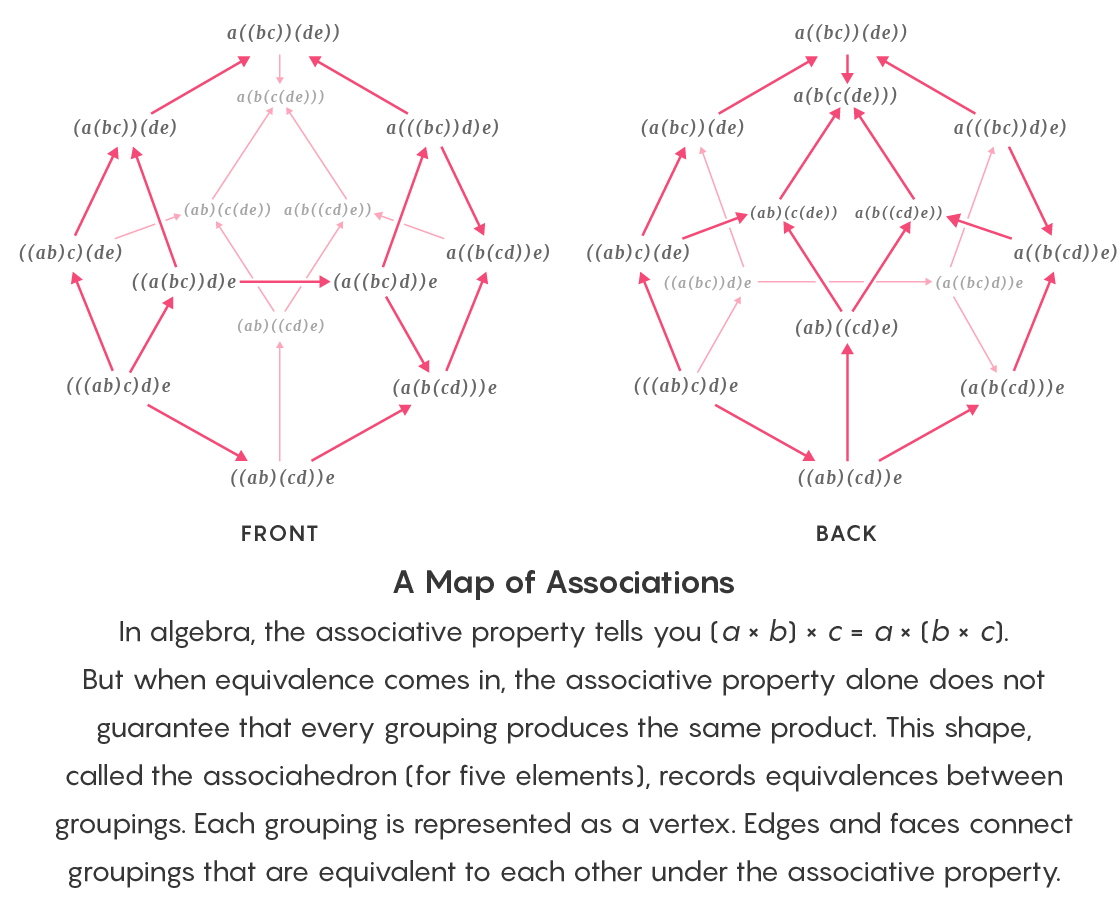En algèbre, l'associativité indique que (a × b) × c = a × (b × c). Mais avec l'utilisation de l'équivalence, l'associativité seule ne garantit pas qu'un groupement d'éléments donnera le même résultat de multiplication. Cet assocaèdre contient des enregistrements d'équivalence de groupe. Chaque sommet correspond à un groupement. Les arêtes et les faces combinent des groupes associativement équivalents les uns aux autres.

"Cela rend le problème extrêmement compliqué, ce qui rend impossible de travailler avec cette nouvelle version des mathématiques", a déclaré David Isla, mathématicien à l'Université du Montana.

En algèbre supérieure, dont la dernière version s'étend sur 1553 pages, Lurie a développé une option d'associativité pour les catégories infinies - ainsi que de nombreux autres théorèmes algébriques qui forment ensemble la base des mathématiques des équivalences.

Ces deux livres ont produit l'effet d'une bombe explosant; ces travaux donnent lieu à une révolution scientifique. "L'échelle était extraordinaire", a déclaré Reel. «C'était la réalisation du niveau de Grothendieck en géométrie algébrique.»

Cependant, la révolution prend du temps et, comme les mathématiciens l’ont découvert après la publication des livres de Lurie, ces années peuvent être chaotiques.

Digérer une vache

Les mathématiciens sont considérés comme des personnes ayant une pensée sans ambiguïté: la preuve est vraie ou non; l'idée fonctionne ou non. Cependant, les mathématiciens sont aussi des gens ordinaires, et ils réagissent aux nouvelles idées de la même manière que les gens ordinaires: subjectivement, émotionnellement, ayant des motifs personnels.

"Je pense que beaucoup de textes ont été écrits sur les mathématiciens dans un ton tel qu'ils recherchent une vérité cristalline étincelante", a déclaré Campbell. "Mais cela ne se produit pas." Ce sont des gens avec leurs propres goûts, zones de confort, et ils peuvent nier des choses qu'ils n'aiment pas pour des raisons esthétiques ou personnelles. "

À cet égard, le travail de Lurie est devenu un défi complexe pour la communauté. En fait, c'était provocateur: voici une nouvelle et meilleure façon de faire les mathématiques. Ce message s'adressait particulièrement aux mathématiciens, qui ont passé toute leur carrière à développer des méthodes que Lurie a excellées.

"Les gens n'aiment pas toujours voir la prochaine génération réécrire leur travail, et ce processus génère du stress", a déclaré Francis. "C'est l'une des caractéristiques de la théorie des catégories de l'infini - la plupart des travaux précédents correspondent."

Le travail de Lurie était difficile à digérer pour d'autres raisons. Le volume de matériel signifiait que les mathématiciens devraient passer des années à lire ses livres. Il est presque impossible d'exiger des mathématiciens occupés qui sont en milieu de carrière, et des étudiants diplômés qui n'ont que quelques années pour donner un résultat leur permettant de trouver un emploi, c'est très risqué.

Le travail de Lurie était également très abstrait, même comparé à la nature extrêmement abstraite de tout ce qui concerne les études mathématiques avancées. Et tout le monde n'a pas aimé. "Beaucoup de gens pensaient que le travail de Lurie était des ordures abstraites, et beaucoup sont tout simplement tombés amoureux d'elle", a déclaré Campbell. «Il y avait des options intermédiaires, y compris celles qui ne la comprenaient pas du tout.»


Bobine d'Emily

La communauté scientifique perçoit constamment de nouvelles idées, mais cela se produit généralement lentement et avec le sentiment que tout le monde bouge en même temps. L'émergence de nouvelles idées crée des difficultés pour l'appareil intellectuel de la communauté. "Beaucoup de nouvelles choses surgissent tout de suite - c'est comme un boa essayant de digérer une vache", a déclaré Campbell. «Une énorme masse traverse la communauté.»

Si vous êtes un mathématicien qui croit que l'approche de Lurie est la meilleure façon de faire des mathématiques, alors votre chemin sera solitaire. Peu de gens lisaient le travail de Lurie, il n’y avait pas de manuels pour les raconter brièvement, ni de séminaires pour vous aider à vous repérer. "Il n'y avait qu'une seule façon d'étudier tout cela en détail - de s'asseoir et de tout faire soi-même", a déclaré Peter Heine, un étudiant diplômé du MIT qui a passé un an à lire le travail de Lurie. - Je pense que c'est le plus difficile. "Il n'est pas facile de s'asseoir et de le découvrir soi-même - à savoir, de s'asseoir et de lire 800 pages de la théorie de la théorie des topos vous-même.

Comme beaucoup de nouvelles inventions, la théorie des topos supérieurs exige que les mathématiciens interagissent activement avec l'appareil, ce qui lui permet de fonctionner.Voici comment faire en sorte que chaque garçon de 16 ans rêvant d'un permis de conduire apprenne d'abord à trier le moteur. "S'il y avait une version plus conviviale de tout cela, alors la théorie deviendrait immédiatement plus accessible à des cercles mathématiques plus larges", a déclaré Dennis Gatesgory, un mathématicien de Harvard qui a travaillé avec Lurie.

Lorsque les gens ont commencé à lire le travail de Lurie et à utiliser les catégories de l'infini dans leurs recherches, d'autres problèmes sont apparus. Les mathématiciens ont construit leur travail sur la base des catégories de l'infini. Les critiques de magazines ont reçu ces articles et ont demandé: qu'est-ce que c'est?

"Il y a eu une situation dans laquelle le travail est revenu des magazines avec des critiques absurdes, d'où un manque total de compréhension était visible, ou il a fallu plusieurs années pour les publier", a déclaré Barvik. «Cela peut être très gênant, car le travail non publié qui est sur votre site depuis des années semble de plus en plus ridicule.»

Cependant, le plus gros problème n'était pas les œuvres non publiées, mais les œuvres utilisant les catégories de l'infini, et publiées - mais contenant des erreurs.

Les livres de Lurie sont la seule source d'information faisant autorité sur les catégories de l'infini. Ils sont stricts, mais il est difficile de les comprendre pleinement. Et ils sont particulièrement mal adaptés au rôle d'instructions qui pourraient être référencées - il est difficile de rechercher certains théorèmes, ou de vérifier qu'une certaine application des catégories d'infini rencontrées dans le travail de quelqu'un fonctionne vraiment.

"La plupart des mathématiciens travaillant dans ce domaine ne lisent pas systématiquement Lurie", a expliqué André Joyal., mathématicien à l'Université du Québec à Montréal, dont les premiers travaux ont été un ingrédient clé dans les livres de Lurie. «Cela prend beaucoup de temps et d'énergie, donc nous supposons simplement que tout ce qui est écrit dans ses livres est vrai - parce que presque chaque fois que nous vérifions quelque chose, cela s'avère vrai. En fait, à chaque fois. "

L'inaccessibilité des livres de Lurie a conduit à des inexactitudes dans certaines des études qui ont suivi. Les livres de Lurie sont difficiles à lire, difficiles à citer et difficiles à utiliser pour tester le travail des autres.

"La littérature générale sur le thème des catégories de l'infini semble désordonnée", a déclaré Zakharevich.

Malgré tout son formalisme, les mathématiques ne doivent pas être un texte sacré que seuls les prêtres peuvent lire. Dans ce domaine, non seulement des volumes épais sont nécessaires, mais aussi des brochures, non seulement les révélations initiales, mais aussi les interprétations de leurs descriptions. En attendant, la théorie des catégories de l'infini existe, pour la plupart, sous la forme de plusieurs grands livres sur une étagère.

"Vous pouvez adopter l'approche." Jacob vous dira quoi faire, et tout va bien ", a déclaré Rezk. "Ou vous pouvez décider que nous ne savons pas comment présenter notre sujet suffisamment bien pour que les gens puissent l'utiliser."

Cependant, peu de mathématiciens ont pu relever le défi et faire de la catégorie de l'infini une technologie que plus de personnes de leur domaine d'étude pourraient utiliser.

Théorie conviviale

Pour traduire les catégories d'infinis en un objet capable d'un véritable travail mathématique, Lurie a dû prouver les théorèmes qui leur sont associés. Et pour cela, il a dû choisir un paysage sur lequel créer cette évidence - tout comme une personne engagée dans la géométrie, il est nécessaire de choisir un système de coordonnées pour le travail. Les mathématiciens appellent cette sélection de modèle.

Lurie a développé les catégories d'infinis sur le modèle des quasicatégories. D'autres mathématiciens avant lui ont développé les catégories d'infinis sur d'autres modèles. Et bien que leur travail ne soit pas aussi complet que celui de Lurie, dans certaines situations, il est plus facile de les traiter. "Jacob a choisi un modèle et vérifié que tout fonctionne bien, mais souvent ce n'est pas le plus simple", a expliqué Zakharevich.

En géométrie, les mathématiciens comprennent clairement comment se déplacer entre différents systèmes de coordonnées. Ils ont également prouvé que les théorèmes se sont avérés dans certaines conditions fonctionner dans d'autres.

Pour les catégories à l'infini, de telles garanties n'existent pas. Cependant, lorsque les mathématiciens écrivent des travaux en utilisant les catégories d'infinis, ils basculent souvent facilement entre les modèles, suggérant (mais ne prouvant pas) la portabilité des résultats. "Les gens ne précisent pas ce qu'ils font, ils basculent entre tous ces différents modèles, et ils disent: Ah, c'est la même chose", a déclaré Heine. "Mais ce n'est pas une preuve."

Au cours des six dernières années, quelques mathématiciens ont tenté d'obtenir ces garanties. Ryl et Dominic Verityde l'Université McUyra en Australie, a développé un moyen de décrire les catégories d'infinis, surmontant les difficultés qui apparaissaient dans les plates-formes précédentes en utilisant certains modèles. Leur travail, basé sur les travaux précédents de Barvik et d'autres, a prouvé que de nombreux théorèmes de la théorie des topos supérieurs restent vrais quel que soit le modèle utilisé. Et ils prouvent cette compatibilité de manière appropriée: «Nous étudions les catégories de l'infini, dont les objets sont eux-mêmes les catégories de l'infini», a expliqué Ril. "La théorie des catégories se mord la queue."

Ril et Verity espèrent développer la théorie des catégories des infinis d'une autre manière encore. Ils choisissent des aspects de la théorie qui fonctionnent indépendamment du modèle. Une telle présentation, indépendante du modèle, présente une qualité pratique d'applicabilité instantanée, qui, espèrent-ils, attirera les mathématiciens dans ce domaine de recherche qui en sont restés à l'écart lorsque la seule entrée était la théorie des topos supérieurs.

"Pour entrer dans ce monde, vous devez surmonter les douves", a déclaré Hopkins. "Et ils font ça en bas du pont."

Ryl et Verity prévoient de terminer leurs travaux l'année prochaine. Pendant ce temps, Lurie a récemment commencé à travailler sur le projet Kerodon., qu'il prévoyait de transformer en une sorte d'ouvrage de référence sur la théorie de la catégorie la plus élevée, semblable à Wikipedia. Treize ans après la formalisation de la théorie des topos sur les mathématiques de l'équivalence, ces initiatives tentent d'affiner et de diffuser ces idées - afin de rendre les mathématiques de l'équivalence plus accessibles.

"Le génie a un rôle important dans le développement des mathématiques, mais la connaissance elle-même est le résultat du travail de toute la communauté", a déclaré Zhoyal. «Le véritable objectif de la connaissance est de devenir une connaissance de l'ensemble de la communauté, et non d'appartenir à une ou deux personnes.»