Sur les traces de
«Our won: TopCoder Open 2019», je publie des tâches de la piste Algorithm
(programmation sportive classique. En une heure et demie, vous devez résoudre trois problèmes en Java, C #, C ++ ou Python.)1. Tarte pour six
Énoncé du problèmeLe délai est de 4 secondes.
Vous avez une tarte. Vu d'en haut, le gâteau a la forme d'un polygone (strictement) convexe. On vous donne les coordonnées des sommets en entiers X et Y.
Tu as cinq amis. Vous voulez diviser le gâteau en six morceaux de surface égale (mais pas nécessairement de la même forme). Bien sûr, n'importe qui peut le faire en cinq coupes, mais seuls les pros peuvent le faire en trois coupes.
Trouvez trois coupes en ligne droite à travers un point qui divisera le gâteau en six morceaux de taille égale. Imprimez {x, y, d1, d2, d3}, où (x, y) est le point commun des trois sections et d1, d2, d3 sont les angles de direction des sections en radians.
DéfinitionClasse: CakeForSix
Méthode: couper
Paramètres: int [], int []
Renvoie: double []
Signature de la méthode: double [] cut (int [] x, int [] y)
(assurez-vous que votre méthode est publique)
Remarques- La direction positive le long de l'axe x est 0 (radian), la direction positive le long de l'axe y est pi / 2 (radian).
- La coupe dans la direction d est similaire à la coupe dans la direction pi * k + d pour tout entier k.
- Vous pouvez sortir toutes les directions, elles ne doivent pas nécessairement provenir de [0, pi).
- La niveleuse calculera la superficie de vos six morceaux de gâteau en double. La réponse sera acceptée si la différence relative ou absolue entre eux est inférieure à 10 ^ (- 4).
- Plus précisément, laissez X et Y être la plus petite et la plus grande de vos six zones calculées par la niveleuse. Votre réponse sera alors acceptée si Y <max (X + 10 ^ (- 4), X * 1 + 10 ^ (- 4))).
- (La version originale du problème utilisait la précision de 1e-7 au lieu de 1e-4. Pour résoudre ce problème dans les archives, la limite de précision a été réduite en raison de la présence de cas d'appel qui rendent très probablement la tâche insoluble avec une précision de 1e-7. Dans un monde idéal, les restrictions ne permettent pas de tels cas et nécessitent toujours une grande précision, il n'est donc pas facile de résoudre le problème avec une optimisation numérique générale.)
Limitations- x contient de 3 à 50 éléments inclus.
- y contient autant d'éléments que x.
- toutes les coordonnées entre 0 et 10 000 inclus
- x et y définissent un polygone convexe dans le sens antihoraire.
Original en anglaisÉnoncé du problème
Le délai est de 4 secondes.
Tu as un gâteau. Vu d'en haut, le gâteau est un polygone (strictement) convexe. On vous donne les coordonnées de ses sommets dans les int [] sx et y.
Tu as cinq amis. Vous voulez maintenant couper le gâteau en six morceaux de surface égale (mais pas nécessairement de forme égale). Bien sûr, tout le monde peut le faire en cinq coupes - mais seul un vrai pro peut le faire en trois!
Trouvez trois coupes rectilignes passant par le même point qui coupent le gâteau en six parties également grandes. Renvoie {x, y, d1, d2, d3}, où (x, y) est le point commun des trois coupes, et d1, d2, d3 sont leurs directions en radians.
Définition
Classe: CakeForSix
Méthode: couper
Paramètres: int [], int []
Renvoie: double []
Signature de la méthode: double [] cut (int [] x, int [] y)
(assurez-vous que votre méthode est publique)
Remarques
- La direction positive le long de l'axe x est 0 (radians), la direction positive le long de l'axe y est pi / 2 (radians).
- Une coupe dans la direction d est la même qu'une coupe dans la direction pi * k + d pour tout entier k.
- Vous pouvez renvoyer toutes les directions, elles ne doivent pas nécessairement provenir de [0, pi).
- La niveleuse calculera les surfaces de vos six morceaux de gâteau en double. La réponse sera acceptée si la différence relative ou absolue entre eux est inférieure à 10 ^ (- 4).
- Plus précisément, laissez X et Y être le plus petit et le plus grand de vos six domaines, tel que calculé par la niveleuse. Ensuite, votre réponse sera acceptée si Y <max (X + 10 ^ (- 4), X * (1 + 10 ^ (- 4))).
- (La version originale du problème utilisait la précision 1e-7 au lieu de 1e-4. Pour résoudre ce problème dans l'archive, la limite de précision a été abaissée en raison de l'existence de cas de contestation qui rendent très probablement la tâche insoluble avec la précision 1e-7. Dans un monde idéal, les contraintes ne permettraient pas de tels cas et nécessitent toujours une grande précision, de sorte qu'il n'est pas facile de résoudre le problème via une optimisation numérique générale.)
Contraintes
- x aura entre 3 et 50 éléments, inclus.
- y aura le même nombre d'éléments que x.
- Toutes les coordonnées seront comprises entre 0 et 10 000, inclus.
- x et y décriront un polygone convexe dans le sens antihoraire.
Des exemples
0){0, 20, 30, 50, 30, 20}
{10, 0, 0, 10, 20, 20}
Retours:
{24.999999999437453, 9.999999999500002, 0.0, 0.7266423406817211, 2.4149503129080787}
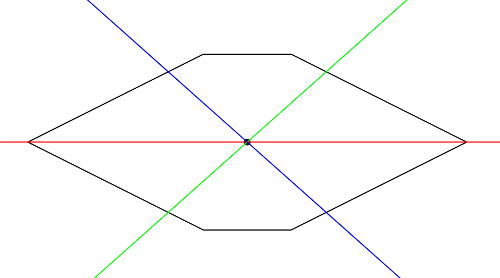
Hexagone symétrique mais pas régulier. Un exemple de réponse correspond à la couper en deux horizontalement et à faire deux autres coupes au centre, qui divisent chaque partie en trois parties.
 1)
1){0, 1000, 0}
{0, 0, 1000}
Retours:
{333.3333333331763, 333.3333333332546, 0.7853981633986264, 2.0344439357948154, 2.6779450445891753}
Triangle droit Encore une fois, nous pouvons commencer par l'une des trois coupes le long de l'axe de symétrie.
 2)
2){40, 70, 90, 90, 50}
{30, 20, 40, 100, 60}
Retours:
{69.79517771922892, 52.77575974637605, 2.0616329654335885, 3.637826104091601, 4.32123485812475}
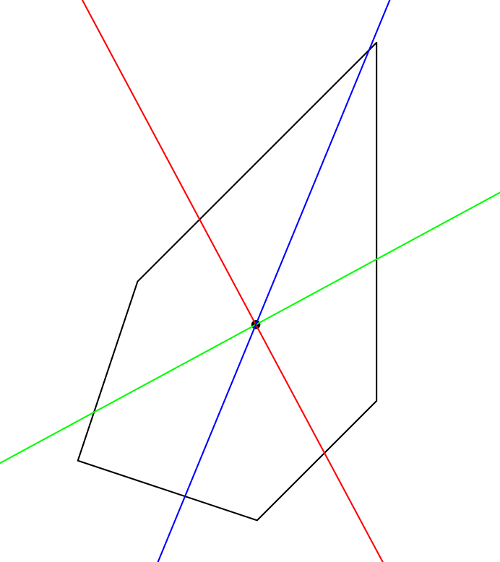
Mauvais pentagone.
 3)
3){300, 400, 300, 200}
{500, 600, 700, 600}
Renvoie: {299.99999999974995, 599.9999999995, 0.0, 1.107148717794088, 2.034443935795705}
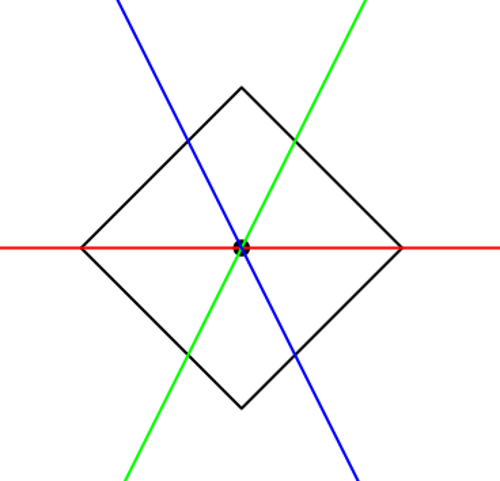
Un carré tournait de 45 degrés.
[
Source ]