Bon après-midi J'ai écrit cet article spécialement pour les étudiants du cours "Algorithmes pour les développeurs" dans OTUS et aujourd'hui je veux le partager avec tous les lecteurs de notre blog.Un cheval d'échecs se tient sur un échiquier et regarde pensivement dans l'échiquier.
Combien de mouvements différents peut-il faire?

Louange à l'inventeur des échecs, il y a
64 cellules sur le plateau.
Louange à l'architecte informatique - le type
ulong a également
64 bits.
Cette coïncidence devait arriver!
L'idée brillante se suggère: stocker la
planche entière en
un seul numéro ! Il y a même un terme spécial pour cette solution -
Bitboard - un bit board.
Alors, comment trouver
rapidement le nombre de mouvements d'un cheval d'échecs en utilisant cette idée?
Donné:
knightNr - numéro de cellule de la planche où se trouve le cheval (de 0 à 63).
Il est nécessaire:
movesCount - le nombre de champs où il peut aller (de 2 à 8).
Algorithme
1. Convertir le numéro de cage du cheval en
ulong - valeur du panneau de mors
knightNr ->
knightBits2. Définissez des bits pour tous les mouvements possibles du cheval
knightBits ->
movesBits3. compter le nombre de bits unitaires
movesBits ->
movesCount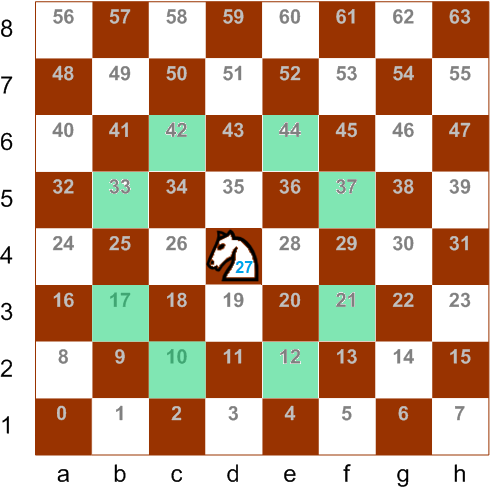
La première étape est très simple, vous devez décaler le bit zéro vers la gauche du nombre de positions spécifié.
ulong knightBits = 1 << knightNr;
La deuxième étape est un peu plus compliquée. Un cheval peut aller dans 8 directions différentes. Nous considérerons ces décalages non pas «horizontalement / verticalement», mais par des positions binaires. Autrement dit, nous considérons le nombre de positions dont vous avez besoin pour décaler le bit de départ pour chaque mouvement. Ensuite, nous «additionnons» tout avec une opération logique «ou».
Commençons par lister les mouvements du côté gauche du plateau vers la droite:
movesBits = knightBits << 6 | knightBits >> 10
Vrai, cool!?
Malheureusement, il y a des «trous noirs» sur les bords de la planche. Par exemple, selon cet algorithme, de la cellule a4 (bit # 24) vous pouvez accéder à la cellule g2 (bit # 14 = 24 - 10), ce saut est une
téléportation d'un cheval d'échecs sphérique dans le vide sur une planche à travers un trou noir vers les verticales extrêmes ...
Pour exclure le saut quantique du cheval sur le bord de la planche, il est nécessaire de «déconnecter» les bandes extrêmes après le déplacement. Par exemple, pour les déplacements +6 et -10 (deux cellules à gauche), il est nécessaire d'annuler les valeurs obtenues sur les verticales g et h, car vous ne pouvez pas vous retrouver sur ces verticales après avoir déplacé «gauche» de deux mouvements.
Pour ce faire, nous avons besoin de constantes de grille de 4 bits, dans lesquelles tous les bits sont définis sur 1, à l'exception des verticales indiquées. À savoir:
ulong nA = 0xFeFeFeFeFeFeFeFe; ulong nAB = 0xFcFcFcFcFcFcFcFc; ulong nH = 0x7f7f7f7f7f7f7f7f; ulong nGH = 0x3f3f3f3f3f3f3f3f;
En haut et en bas de l'échiquier, il y a également des «trous noirs» qui absorbent complètement le cheval, il n'est donc pas nécessaire de les vérifier séparément.
Maintenant, l'algorithme pour générer des mouvements de chevaux autorisés ressemble à ceci:
movesBits = nGH & (knightBits << 6 | knightBits >> 10) | nH & (knightBits << 15 | knightBits >> 17) | nA & (knightBits << 17 | knightBits >> 15) | nAB & (knightBits << 10 | knightBits >> 6);
Cela fonctionne très (!) Rapidement.
Quelques tiques - et nous avons une image bitmap de toutes les aventures de chevaux possibles. La chose la plus étonnante est que cet algorithme fonctionne bien même s'il y a plusieurs chevaux sur la planche. Il génère immédiatement tous les mouvements possibles pour tous les chevaux! C'est vrai, super!?
Reste à compter le nombre de bits
Le moyen le plus simple consiste à décaler le bit numéro 1 vers la droite et à compter ceux. Difficulté - 64 opérations. Mémoire - 64 bits.
Le moyen le plus rapide consiste à créer un cache / tableau avec 65536 éléments, dans lequel le nombre de bits pour chaque index est écrit de 0 à 65535. Et ajoutez 4 éléments de ce tableau qui correspondent aux segments 16 bits suivants du nombre.
Difficulté - 4 opérations. Mémoire - 64 kilo-octets.
Mais nous considérerons la
manière la
plus délicate , dont la complexité est égale au nombre de bits simples dans le nombre. Puisqu'il n'y a pas beaucoup de mouvements, cette approche sera la plus optimale pour nous.
Pour commencer, nous notons qu'en soustrayant une unité d'un nombre, nous transformons tous les «bons» zéros en unités et l'unité la plus externe en zéro:
1001010100010000 - 1 = 1001010100001111
Ensuite, appliquez l'opération logique «et» pour ces nombres:
1001010100010000 & 1001010100001111 = 1001010100000000
Comme vous pouvez le voir, d'une manière si délicate, nous remettons à zéro l'unité la plus à droite. Répétez cette opération jusqu'à ce que nous obtenions zéro en conséquence. Combien d'itérations, tant de bits simples. C'est vrai, super!?
Voici comment cet algorithme est écrit dans son intégralité:
int movesCount = 0; while (movesBits != 0) { movesBits &= (movesBits - 1); movesCount ++; }
Le problème est résolu!
Cette tâche a une autre solution, très simple, purement logique: déterminer la distance du chevalier par rapport au bord de l'échiquier (dans le coin, il y a 2 mouvements, près du bord de 3 à 6 mouvements, au centre de 8 mouvements). Mais si nous devions résoudre le problème "de front" de cette manière, nous ne saurions rien sur le panneau de bits, sur les masques de bits verticaux, sur l'algorithme de comptage rapide des bits simples et sur les trous noirs pour les chevaux sphériques dans le vide ...
Maintenant, nous savons tout. La vie d'un programmeur d'échecs est devenue plus riche et plus significative, bravo!
Tâche de bricolage: faites de même pour le roi d'échecs.