La traduction de l'article a été préparée spécialement pour les étudiants du cours Machine Learning .
La formation renforcée a pris le monde de l'intelligence artificielle. À partir d'AlphaGo et d'
AlphaStar , un nombre croissant d'activités qui étaient auparavant dominées par les humains sont désormais conquises par des agents de l'IA basés sur la formation de renforcement. En bref, ces réalisations dépendent de l'optimisation des actions de l'agent dans un environnement particulier pour obtenir une récompense maximale. Dans les derniers articles de
GradientCrescent, nous avons examiné divers aspects fondamentaux de l'apprentissage renforcé, depuis les bases des systèmes de
bandits et
des approches basées sur les
politiques jusqu'à l'optimisation du comportement basé sur
les récompenses dans
les environnements Markov . Toutes ces approches nécessitaient une connaissance complète de notre environnement.
La programmation dynamique , par exemple, nécessite que nous ayons une distribution de probabilité complète de toutes les transitions d'état possibles. Cependant, en réalité, nous constatons que la plupart des systèmes ne peuvent pas être entièrement interprétés et que les distributions de probabilité ne peuvent pas être obtenues explicitement en raison de la complexité, de l'incertitude inhérente ou des limitations des capacités de calcul. Par analogie, considérons la tâche du météorologue - le nombre de facteurs impliqués dans les prévisions météorologiques peut être si grand qu'il est impossible de calculer avec précision la probabilité.
Dans de tels cas, des méthodes d'enseignement telles que Monte Carlo sont la solution. Le terme Monte Carlo est couramment utilisé pour décrire toute approche d'estimation d'échantillonnage aléatoire. En d'autres termes, nous ne prédisons pas les connaissances sur notre environnement, mais apprenons de l'expérience en passant par des séquences exemplaires d'états, d'actions et de récompenses obtenues à la suite d'une interaction avec l'environnement. Ces méthodes fonctionnent en observant directement les récompenses retournées par le modèle en fonctionnement normal afin de juger de la valeur moyenne de ses conditions. Fait intéressant, même sans aucune connaissance de la dynamique de l'environnement (qui devrait être considérée comme la distribution de probabilité des transitions d'état), nous pouvons toujours obtenir un comportement optimal pour maximiser les récompenses.
À titre d'exemple, considérons le résultat d'un lancer de 12 dés. En considérant ces lancers comme un seul état, nous pouvons faire la moyenne de ces résultats afin de nous rapprocher du vrai résultat prédit. Plus l'échantillon est grand, plus nous nous rapprocherons avec précision du résultat réel attendu.
Le montant moyen attendu sur 12 dés pour 60 tirs est de 41,57Ce type d'évaluation basée sur l'échantillonnage peut sembler familier au lecteur, car un tel échantillonnage est également effectué pour les systèmes à k-bandit. Au lieu de comparer différents bandits, les méthodes de Monte Carlo sont utilisées pour comparer différentes politiques dans les environnements Markov, en déterminant la valeur de l'état lorsqu'une certaine politique est suivie jusqu'à ce que le travail soit terminé.
Estimation de Monte Carlo de la valeur d'état
Dans le contexte de l'apprentissage par renforcement, les méthodes de Monte Carlo sont un moyen d'évaluer la signification de l'état d'un modèle en faisant la moyenne des résultats des échantillons. En raison de la nécessité d'un état terminal, les méthodes de Monte Carlo sont intrinsèquement applicables aux environnements épisodiques. En raison de cette limitation, les méthodes Monte Carlo sont généralement considérées comme «autonomes» dans lesquelles toutes les mises à jour sont effectuées après avoir atteint l'état terminal. Une analogie simple avec la recherche d'un moyen de sortir d'un labyrinthe peut être donnée - une approche autonome obligerait l'agent à atteindre la fin avant d'utiliser l'expérience intermédiaire acquise pour essayer de réduire le temps qu'il faut pour traverser le labyrinthe. D'un autre côté, avec l'approche en ligne, l'agent changera constamment son comportement déjà lors du passage du labyrinthe, peut-être qu'il remarquera que les couloirs verts mènent à des impasses et décidera de les éviter, par exemple. Nous discuterons des approches en ligne dans l'un des articles suivants.
La méthode de Monte Carlo peut être formulée comme suit:
Pour mieux comprendre le fonctionnement de la méthode Monte Carlo, considérez le diagramme de transition d'état ci-dessous. La récompense pour chaque transition d'état est affichée en noir, un facteur d'actualisation de 0,5 lui est appliqué. Mettons de côté la valeur réelle de l'état et concentrons-nous sur le calcul des résultats d'un lancer.
Diagramme de transition d'état. Le numéro d'état est affiché en rouge, le résultat est noir.Étant donné que l'état terminal renvoie un résultat égal à 0, calculons le résultat de chaque état, en commençant par l'état terminal (G5). Veuillez noter que nous avons fixé le facteur d'actualisation à 0,5, ce qui entraînera une pondération vers les États ultérieurs.
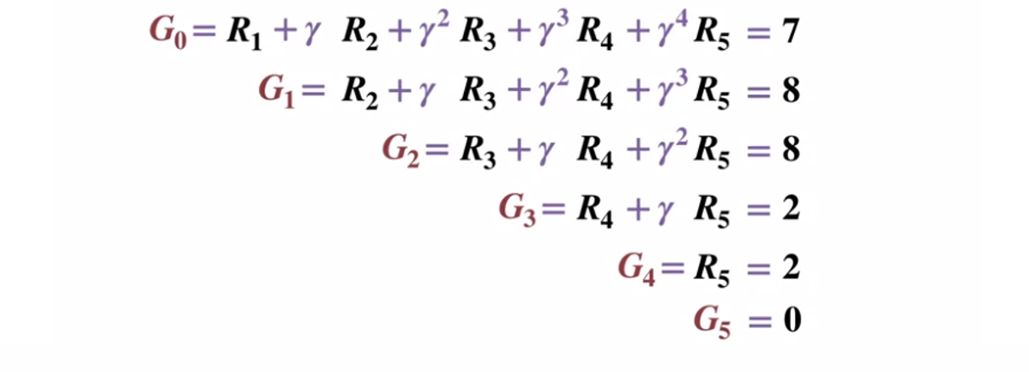
Ou plus généralement:
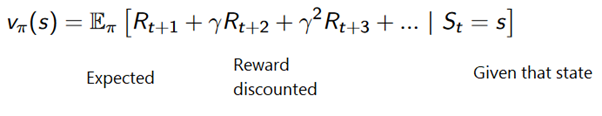
Pour éviter de stocker tous les résultats dans la liste, nous pouvons effectuer la procédure de mise à jour progressive de la valeur d'état dans la méthode de Monte Carlo, en utilisant une équation qui présente quelques similitudes avec la descente de gradient traditionnelle:
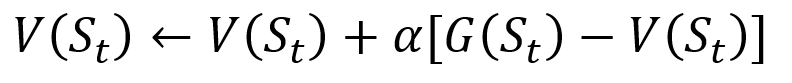Procédure de mise à jour incrémentielle de Monte Carlo. S est l'état, V est sa valeur, G est son résultat et A est le paramètre de valeur de pas.Dans le cadre de la formation de renforcement, les méthodes de Monte Carlo peuvent même être classées en première visite ou à chaque visite. En bref, la différence entre les deux est le nombre de fois qu'un état peut être visité par un passage avant la mise à jour de Monte Carlo. La méthode Monte Carlo First-visit estime la valeur de tous les états comme la valeur moyenne des résultats après des visites uniques dans chaque état avant la fin, tandis que la méthode Monte Carlo Every visit fait la moyenne des résultats après n visites jusqu'à la fin. Nous utiliserons la première visite de Monte Carlo tout au long de cet article en raison de sa relative simplicité.
Monte Carlo Policy Management
Si le modèle ne peut pas fournir la politique, Monte Carlo peut être utilisé pour évaluer les valeurs d'état-action. Ceci est plus utile que la simple signification des états, car l'idée de la signification de chaque action
(q) dans un état donné permet à l'agent de formuler automatiquement une politique à partir d'observations dans un environnement inconnu.
Plus formellement, nous pouvons utiliser Monte Carlo pour estimer
q (s, a, pi) , le résultat attendu en partant de l'état s, de l'action a et de la politique
Pi suivante . Les méthodes de Monte-Carlo restent les mêmes, sauf qu'il existe une dimension supplémentaire des actions entreprises pour un certain état. On pense qu'une paire état-action
(s, a) est visitée pendant le passage si l'état
s est jamais visité et que l'action
a y est effectuée. De même, l'évaluation des actions de valeur peut être réalisée en utilisant les approches «Première visite» et «Chaque visite».
Comme dans la programmation dynamique, nous pouvons utiliser une politique d'itération généralisée (GPI) pour former une politique à partir de l'observation des valeurs d'état-action.
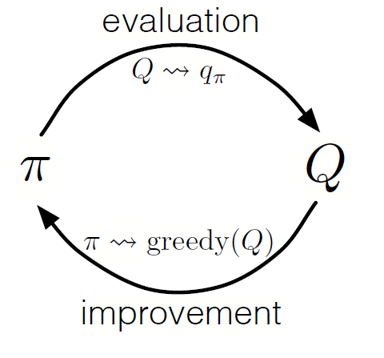
En alternant les étapes de l'évaluation et de l'amélioration des politiques, et en incluant des recherches pour s'assurer que toutes les actions possibles sont visitées, nous pouvons atteindre la politique optimale pour chaque condition. Pour le Monte Carlo GPI, cette rotation se fait généralement après la fin de chaque passage.
Monte Carlo GPIStratégie de Blackjack
Pour mieux comprendre comment la méthode de Monte Carlo fonctionne dans la pratique pour évaluer différentes valeurs d'état, prenons une démonstration étape par étape de l'exemple d'un jeu de blackjack. Pour commencer, déterminons les règles et conditions de notre jeu:
- Nous jouerons uniquement contre le croupier, il n'y aura pas d'autres joueurs. Cela nous permettra de considérer les mains du concessionnaire comme faisant partie de l'environnement.
- La valeur des cartes avec des nombres égaux aux valeurs nominales. La valeur des cartes illustrées: Jack, King and Queen est de 10. La valeur de l'as peut être de 1 ou 11 selon le choix du joueur.
- Les deux camps reçoivent deux cartes. Deux cartes de joueur sont face visible, une des cartes du croupier est également face visible.
- Le but du jeu est que le nombre de cartes en main soit <= 21. Une valeur supérieure à 21 est un buste, si les deux côtés ont une valeur de 21, alors le jeu se joue en match nul.
- Une fois que le joueur a vu ses cartes et la première carte du croupier, le joueur peut choisir de lui prendre une nouvelle carte ("encore") ou non ("assez") jusqu'à ce qu'il soit satisfait de la somme des valeurs de carte dans sa main.
- Ensuite, le croupier montre sa deuxième carte - si le montant résultant est inférieur à 17, il est obligé de prendre des cartes jusqu'à ce qu'il atteigne 17 points, après quoi il ne prend plus la carte.
Voyons comment la méthode Monte Carlo fonctionne avec ces règles.
Tour 1.
Vous gagnez un total de 19. Mais vous essayez d'attraper la chance par la queue, de prendre une chance, d'en obtenir 3 et de vous ruiner. Lorsque vous avez fait faillite, le croupier n'avait qu'une seule carte ouverte avec une somme de 10. Cela peut être représenté comme suit:
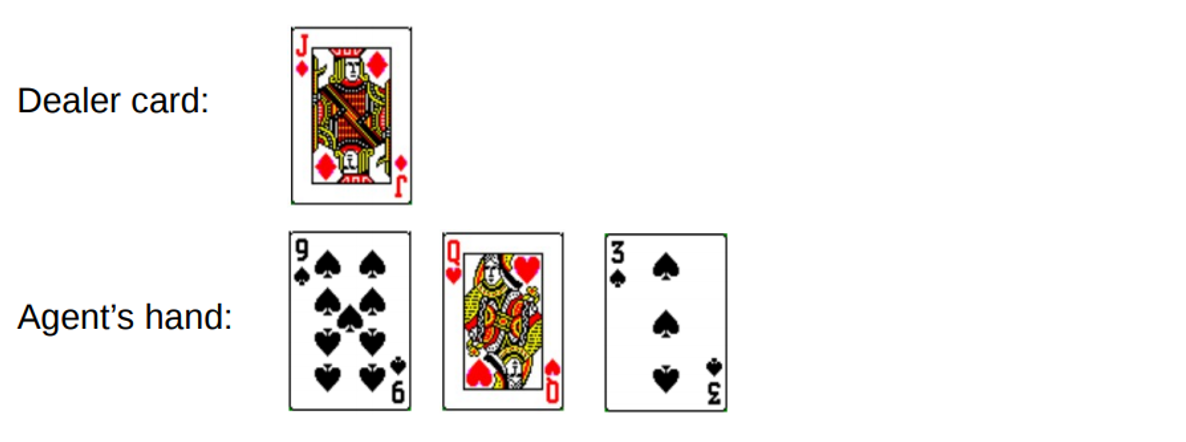
Si nous faisons faillite, notre récompense pour la manche est de -1. Définissons cette valeur comme le résultat de retour de l'avant-dernier état, en utilisant le format suivant [Montant de l'agent, Montant du concessionnaire, as?]:
Eh bien, maintenant nous n'avons plus de chance. Passons à un autre tour.
Tour 2.
Vous tapez un total de 19. Cette fois, vous décidez d'arrêter. Le croupier compose le 13, prend une carte et fait faillite. L'avant-dernier état peut être décrit comme suit.
Décrivons les conditions et les récompenses que nous avons reçues lors de ce tour:
Avec la fin du passage, nous pouvons maintenant mettre à jour les valeurs de tous nos états dans ce tour en utilisant les résultats calculés. En prenant un facteur de remise de 1, nous répartissons simplement notre nouvelle récompense de main, comme cela a été fait avec les transitions d'état plus tôt. Puisque l'état
V (19, 10, non) a précédemment renvoyé -1, nous calculons la valeur de retour attendue et l'affectons à notre état:
Valeurs d'état final pour la démonstration en utilisant le blackjack comme exemple .
Implémentation
Écrivons un jeu de blackjack en utilisant la méthode Monte Carlo de la première visite pour découvrir toutes les valeurs d'état possibles (ou diverses combinaisons disponibles) dans le jeu en utilisant Python. Notre approche sera basée sur l'
approche de Sudharsan et. al. . Comme d'habitude, vous pouvez retrouver tout le code de l'article sur
notre GitHub .
Pour simplifier la mise en œuvre, nous utiliserons gym d'OpenAI. Considérez l'environnement comme une interface pour démarrer le blackjack avec une quantité minimale de code, cela nous permettra de nous concentrer sur la mise en œuvre d'un apprentissage renforcé. Idéalement, toutes les informations collectées sur les états, les actions et les récompenses sont stockées dans les variables
«observation» , qui sont accumulées pendant les sessions de jeu en cours.
Commençons par importer toutes les bibliothèques dont nous avons besoin pour obtenir et collecter nos résultats.
import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use('ggplot')
Ensuite, initialisons notre environnement de
gym et définissons une politique qui coordonnera les actions de notre agent. En fait, nous continuerons à prendre la carte jusqu'à ce que le montant en main atteigne 19 ou plus, après quoi nous nous arrêterons.
Définissons une méthode pour générer des données de passe à l'aide de notre politique. Nous conserverons des informations sur l'état, les actions entreprises et les récompenses de l'action.
def generate_episode(policy, env):
Enfin, définissons la première visite de la fonction de prédiction Monte Carlo. Tout d'abord, nous initialisons un dictionnaire vide pour stocker les valeurs de l'état actuel et un dictionnaire qui stocke le nombre d'enregistrements pour chaque état dans différentes passes.
def first_visit_mc_prediction(policy, env, n_episodes):
Pour chaque passage, nous appelons notre méthode
generate_episode pour obtenir des informations sur les valeurs d'état et les récompenses reçues après que l'état se soit produit. Nous initialisons également la variable pour stocker nos résultats incrémentiels. Ensuite, nous obtenons la récompense et la valeur de l'état actuel pour chaque état visité pendant le passage, et augmentons nos rendements variables de la valeur de la récompense par étape.
for _ in range(n_episodes):
Permettez-moi de vous rappeler que puisque nous mettons en œuvre la première visite de Monte-Carlo, nous visitons un État en un seul passage. Par conséquent, nous effectuons une vérification conditionnelle du dictionnaire d'état pour voir si l'état a été visité. Si cette condition est remplie, nous sommes en mesure de calculer la nouvelle valeur en utilisant la procédure précédemment définie pour mettre à jour les valeurs d'état en utilisant la méthode de Monte Carlo et d'augmenter le nombre d'observations pour cet état de 1. Ensuite, nous répétons le processus pour la prochaine passe afin d'obtenir finalement la valeur moyenne du résultat .
Lançons ce que nous avons obtenu et regardons les résultats!
value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000) for i in range(10): print(value.popitem())
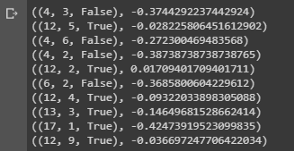Conclusion d'un échantillon montrant les valeurs d'état de diverses combinaisons sur les mains au blackjack.Nous pouvons continuer à faire des observations de Monte Carlo pour 5000 passes et construire une distribution des valeurs d'état qui décrit les valeurs de n'importe quelle combinaison entre les mains du joueur et du croupier.
def plot_blackjack(V, ax1, ax2): player_sum = np.arange(12, 21 + 1) dealer_show = np.arange(1, 10 + 1) usable_ace = np.array([False, True]) state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace))) for i, player in enumerate(player_sum): for j, dealer in enumerate(dealer_show): for k, ace in enumerate(usable_ace): state_values[i, j, k] = V[player, dealer, ace] X, Y = np.meshgrid(player_sum, dealer_show) ax1.plot_wireframe(X, Y, state_values[:, :, 0]) ax2.plot_wireframe(X, Y, state_values[:, :, 1]) for ax in ax1, ax2: ax.set_zlim(-1, 1) ax.set_ylabel('player sum') ax.set_xlabel('dealer sum') ax.set_zlabel('state-value') fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'}) axes[0].set_title('state-value distribution w/o usable ace') axes[1].set_title('state-value distribution w/ usable ace') plot_blackjack(value, axes[0], axes[1])
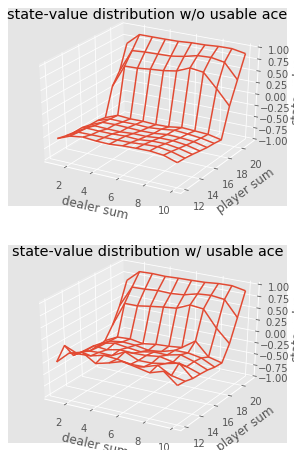Visualisation des valeurs d'état de diverses combinaisons au blackjack.Résumons donc ce que nous avons appris.
- Les méthodes d'apprentissage basées sur l'échantillonnage nous permettent d'évaluer les valeurs d'état et d'action-état sans aucune dynamique de transition, simplement par échantillonnage.
- Les approches de Monte Carlo sont basées sur un échantillonnage aléatoire du modèle, en observant les récompenses retournées par le modèle et en collectant des informations pendant le fonctionnement normal pour déterminer la valeur moyenne de ses états.
- En utilisant les méthodes de Monte Carlo, une politique d'itération généralisée est possible.
- La valeur de toutes les combinaisons possibles entre les mains du joueur et du croupier au blackjack peut être estimée en utilisant plusieurs simulations de Monte Carlo, ouvrant la voie à des stratégies optimisées.
Ceci conclut l'introduction à la méthode de Monte Carlo. Dans notre prochain article, nous passerons aux méthodes d'enseignement sous la forme d'apprentissage de la différence temporelle.
Sources:
Sutton et. al, Renforcement Learning
White et. al, Fundamentals of Reinforcement Learning, Université de l'Alberta
Silva et. al, apprentissage par renforcement, UCL
Platt et. Al, Université de NortheasterC’est tout. Rendez-vous sur le
parcours !