L'optimisation des compilateurs est la base des logiciels modernes: ils permettent aux programmeurs d'écrire du code dans un langage qu'ils comprennent, puis de le convertir en code qui peut être exécuté efficacement par l'équipement. L'optimisation des compilateurs consiste à comprendre ce que fait le programme d'entrée que vous avez écrit et à créer un programme de sortie qui fait la même chose, mais plus rapidement.
Dans cet article, nous examinerons certaines des techniques d'inférence de base dans l'optimisation des compilateurs: comment concevoir un programme avec lequel le compilateur peut facilement travailler; quelles réductions peuvent être faites dans votre programme et comment les utiliser pour le réduire et l'accélérer.
Les optimiseurs de programme peuvent fonctionner n'importe où: dans le cadre d'un processus de compilation important (
Scala Optimizer ); en tant que programme distinct, lancé après le compilateur et avant exécution (
Proguard ); ou dans le cadre d'un environnement d'exécution qui optimise un programme lors de son exécution (
compilateur JVM JIT ). Les limitations dans le travail des optimiseurs varient selon la situation, mais ils ont une tâche: prendre le programme d'entrée et le convertir en celui de sortie, ce qui fait la même chose, mais plus rapidement.
Tout d'abord, nous allons examiner quelques exemples d'optimisations pour le projet de programme afin que vous compreniez ce que les optimiseurs font habituellement et comment le faire manuellement. Ensuite, nous examinerons plusieurs façons de présenter les programmes, et enfin nous analyserons les algorithmes et les techniques avec lesquels vous pouvez analyser les programmes, puis les rendre plus petits et plus rapides.
Projet de programme
Tous les exemples seront donnés en Java. Ce langage est très courant et se compile en un assembleur relativement simple -
Java Bytecode . Nous allons donc créer une bonne base, grâce à laquelle nous pouvons explorer des techniques d'optimisation de la compilation à l'aide d'exemples réels et exécutables. Toutes les techniques décrites ci-dessous sont applicables dans presque tous les autres langages de programmation.
Examinons d'abord un projet de programme. Il contient diverses logiques, enregistre le résultat standard dans le processus et renvoie le résultat calculé. Le programme lui-même n'a pas de sens, mais sera utilisé comme illustration de ce qui peut être optimisé tout en conservant le comportement existant:
static int main(int n){ int count = 0, total = 0, multiplied = 0; Logger logger = new PrintLogger(); while(count < n){ count += 1; multiplied *= count; if (multiplied < 100) logger.log(count); total += ackermann(2, 2); total += ackermann(multiplied, n); int d1 = ackermann(n, 1); total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
Pour l'instant, nous supposons que ce programme est tout ce que nous avons, aucune autre partie du code ne l'appelle. Il saisit simplement les données dans
main , l'exécute et renvoie le résultat. Maintenant, optimisons ce programme.
Exemples d'optimisation
Type coulée et inlining
Vous avez peut-être remarqué que la variable de l'
logger a un type inexact: malgré l'étiquette de l'
Logger , basée sur le code, nous pouvons conclure qu'il s'agit d'une sous-classe spécifique -
PrintLogger :
- Logger logger = new PrintLogger(); + PrintLogger logger = new PrintLogger();
Nous savons maintenant que
logger est
PrintLogger et nous savons que l'appel à
logger.log peut avoir une seule implémentation. Vous pouvez incorporer:
- if (multiplied < 100) logger.logcount(); + if (multiplied < 100) System.out.println(count);
Cela réduira le programme en supprimant la classe
ErrLogger inutile, qui n'est pas utilisée, ainsi qu'en supprimant diverses méthodes du
log public Logger , car nous l'intégrons au même endroit de l'appel.
Constantes de coagulation
Pendant l'exécution du programme, le
count et
total changement
total , mais pas
multiplied : il commence à
0 et est multiplié à chaque fois par
multiplied = multiplied * count , restant égal à
0 . Vous pouvez donc le remplacer dans tout le programme par
0 :
static int main(int n){ - int count = 0, total = 0, multiplied = 0; + int count = 0, total = 0; PrintLogger logger = new PrintLogger(); while(count < n){ count += 1; - multiplied *= count; - if (multiplied < 100) System.out.println(count); + if (0 < 100) logger.log(count); total += ackermann(2, 2); - total += ackermann(multiplied, n); + total += ackermann(0, n); int d1 = ackermann(n, 1); - total += d1 * multiplied; int d2 = ackermann(n, count); if (count % 2 == 0) total += d2; } return total; }
En conséquence, nous voyons que
d1 * multiplied toujours
0 , ce qui signifie que le
total += d1 * multiplied ne fait rien et peut être supprimé:
- total += d1 * multiplied
Suppression du code mort
Après avoir plié
multiplied et réalisé que le
total += d1 * multiplied ne fait rien, vous pouvez supprimer la définition de
int d1 :
- int d1 = ackermann(n, 1);
Cela ne fait plus partie du programme, et comme
ackermann est une fonction pure, la désinstallation n'affectera pas le résultat du programme.
De même, après avoir inséré
logger.log , l'
logger lui-même n'est plus utilisé et peut être supprimé:
- PrintLogger logger = new PrintLogger();
Suppression de branche
Maintenant, la première transition conditionnelle de notre cycle dépend de
0 < 100 . Comme cela est toujours vrai, vous pouvez simplement supprimer la condition:
- if (0 < 100) System.out.println(count); + System.out.println(count);
Toute transition conditionnelle toujours vraie peut être insérée dans le corps de la condition, et pour les transitions toujours incorrectes, vous pouvez supprimer la condition avec son corps.
Calcul partiel
Nous analysons maintenant les trois appels restants à
ackermann :
total += ackermann(2, 2); total += ackermann(0, n); int d2 = ackermann(n, count);
- Le premier a deux arguments constants. La fonction est pure, et lors du calcul préliminaire,
ackermann(2, 2) doit être égal à 7. - Le deuxième appel a un argument constant
0 et un n inconnu. Vous pouvez le passer à la définition de ackermann , et il s'avère que lorsque m est 0 , la fonction retourne toujours n + 1.
- Dans le troisième appel, les deux arguments sont inconnus:
n et count . Laissons-les en place pour l'instant.
Étant donné que l'appel à
ackermann est défini comme suit:
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Vous pouvez le simplifier pour:
- total += ackermann(2, 2); + total += 7 - total += ackermann(0, n); + total += n + 1 int d2 = ackermann(n, count);
Planification tardive
La définition de
d2 utilisée que dans le
if (count % 2 == 0) conditionnel
if (count % 2 == 0) . Étant donné que le calcul
ackermann est propre, vous pouvez transférer cet appel vers une
ackermann conditionnelle afin qu'il ne soit traité que lorsqu'il est utilisé:
- int d2 = ackermann(n, count); - if (count % 2 == 0) total += d2; + if (count % 2 == 0) { + int d2 = ackermann(n, count); + total += d2; + }
Cela évitera la moitié des appels à
ackermann(n, count) , accélérant ainsi l'exécution du programme.
À titre de comparaison, la fonction
System.out.println n'est pas propre, ce qui signifie qu'elle ne peut pas être transférée à l'intérieur ou à l'extérieur des sauts conditionnels sans modifier la sémantique du programme.
Résultat optimisé
Après avoir collecté toutes les optimisations, nous obtenons le code source suivant:
static int main(int n){ int count = 0, total = 0; while(count < n){ count += 1; System.out.println(count); total += 7; total += n + 1; if (count % 2 == 0) { total += d2; int d2 = ackermann(n, count); } } return total; } static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Bien que nous ayons optimisé manuellement, tout cela peut se faire automatiquement. Voici le résultat décompilé de l'optimiseur de prototype que j'ai écrit pour les programmes JVM:
static int main(int var0) { new Demo.PrintLogger(); int var1 = 0; int var3; for(int var2 = 0; var2 < var0; var2 = var3) { System.out.println(var3 = 1 + var2); int var10000 = var3 % 2; int var7 = var1 + 7 + var0 + 1; var1 = var10000 == 0 ? var7 + ackermann(var0, var3) : var7; } return var1; } static int ackermann__I__TI1__I(int var0) { if (var0 == 0) return 2; else return ackermann(var0 - 1, var0 == 0 ? 1 : ackermann__I__TI1__I(var0 - 1);); } static int ackermann(int var0, int var1) { if (var0 == 0) return var1 + 1; else return var1 == 0 ? ackermann__I__TI1__I(var0 - 1) : ackermann(var0 - 1, ackermann(var0, var1 - 1)); } static class PrintLogger implements Demo.Logger {} interface Logger {}
Le code décompilé est légèrement différent de la version optimisée manuellement. Quelque chose que le compilateur n'a pas pu optimiser (par exemple, un appel inutilisé à
new PrintLogger ), mais quelque chose a été fait un peu différemment (par exemple,
ackermann et
ackermann__I__TI1__I ). Mais pour le reste, l'optimiseur automatique a fait la même chose que moi, en utilisant la logique intégrée.
La question se pose: comment?
Vues intermédiaires
Si vous essayez de créer votre propre optimiseur, la première question qui se posera sera peut-être la plus importante: qu'est-ce qu'un «programme»?
Sans aucun doute, vous avez l'habitude d'écrire et de modifier des programmes sous forme de code source. Vous les avez certainement exécutés sous forme de binaires compilés, peut-être même débogué les binaires. Vous avez peut-être rencontré des programmes sous la forme d'une
arborescence de syntaxe , d'un
code à trois adresses , d'un
A-Normal , d'un
style de passage continu ou d'
une affectation statique unique .
Il y a tout un zoo de différentes représentations de programmes. Ici, nous allons discuter des façons les plus importantes de représenter un «programme» à l'intérieur de l'optimiseur.
Code source
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Le code source non compilé est également une représentation de votre programme. Il est relativement compact, lisible par l'homme, mais il présente deux inconvénients:
- Le code source contient tous les détails des noms et du formatage, qui sont importants pour le programmeur, mais inutiles pour l'ordinateur.
- Il y a beaucoup plus de programmes erronés sous forme de code source que de programmes corrects, et pendant l'optimisation, vous devez vous assurer que votre programme est converti du code source d'entrée correct au code source de sortie correct.
Ces facteurs rendent difficile pour l'optimiseur de travailler avec le programme sous forme de code source. Oui, vous
pouvez convertir un tel programme, par exemple, en utilisant
des expressions régulières pour identifier et remplacer des modèles. Cependant, le premier des deux facteurs rend difficile l'identification fiable de modèles avec une abondance de détails étrangers. Et le deuxième facteur augmente considérablement les risques de confusion et d'obtenir un programme résultant incorrect.
Ces restrictions sont acceptables pour les convertisseurs de programme exécutés sous supervision humaine, par exemple, lorsque vous pouvez utiliser
Codemod pour refactoriser et transformer la base de code. Cependant, vous ne pouvez pas utiliser le code source comme modèle principal d'un optimiseur automatisé.
Arbres de syntaxe abstraite
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); } IfElse( cond = BinOp(Ident("m"), "=", Literal(0)), then = Return(BinOp(Ident("n"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("n"), "=", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("m"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("m"), "-", Literal(1)), Call("ackermann", Ident("m"), BinOp(Ident("n"), "-", Literal(1))) ) ) ) )

Les arbres de syntaxe abstraite (AST) sont un autre format intermédiaire commun. Ils sont situés à l'étape suivante de l'échelle d'abstraction par rapport au code source. En règle générale, AST ignore la mise en forme, l'indentation et les commentaires du code source, mais conserve les noms des variables locales qui sont ignorées dans les représentations plus abstraites.
Comme le code source, AST souffre de la possibilité d'encoder des informations inutiles qui n'affectent pas la sémantique réelle du programme. Par exemple, les deux fragments de code suivants sont sémantiquement identiques; ils ne diffèrent que par le nom des variables locales, mais ont toujours des AST différents:
static int ackermannA(int m, int n){ int p = n; int q = m; if (q == 0) return p + 1; else if (p == 0) return ackermannA(q - 1, 1); else return ackermannA(q - 1, ackermannA(q, p - 1)); } Block( Assign("p", Ident("n")), Assign("q", Ident("m")), IfElse( cond = BinOp(Ident("q"), "==", Literal(0)), then = Return(BinOp(Ident("p"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("p"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("q"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("q"), "-", Literal(1)), Call("ackermann", Ident("q"), BinOp(Ident("p"), "-", Literal(1))) ) ) ) ) ) static int ackermannB(int m, int n){ int r = n; int s = m; if (s == 0) return r + 1; else if (r == 0) return ackermannB(s - 1, 1); else return ackermannB(s - 1, ackermannB(s, r - 1)); } Block( Assign("r", Ident("n")), Assign("s", Ident("m")), IfElse( cond = BinOp(Ident("s"), "==", Literal(0)), then = Return(BinOp(Ident("r"), "+", Literal(1)), else = IfElse( cond = BinOp(Ident("r"), "==", Literal(0)), then = Return(Call("ackermann", BinOp(Ident("s"), "-", Literal(1)), Literal(1)), else = Return( Call( "ackermann", BinOp(Ident("s"), "-", Literal(1)), Call("ackermann", Ident("s"), BinOp(Ident("r"), "-", Literal(1))) ) ) ) ) )
Le point clé est que, bien que les AST aient une structure arborescente, ils contiennent des nœuds qui se comportent sémantiquement pas comme des arbres: les valeurs de
Ident("r") et
Ident("s") déterminées non pas par le contenu de leurs sous-arbres, mais par les nœuds
Assign("r", ...) node
Assign("r", ...) amont)
Assign("r", ...) et
Assign("s", ...) . En fait, il existe des relations sémantiques supplémentaires entre les
Ident et les
Assign qui sont tout aussi importantes que les arêtes dans la structure arborescente AST:

Ces connexions forment une structure graphique généralisée, comprenant des cycles en présence de définitions récursives de fonctions.
Bytecode
Depuis que nous avons choisi Java comme langue principale, les programmes compilés sont enregistrés en tant que bytecode Java dans des fichiers .class.
Rappelons notre fonction
ackermann :
static int ackermann(int m, int n){ if (m == 0) return n + 1; else if (n == 0) return ackermann(m - 1, 1); else return ackermann(m - 1, ackermann(m, n - 1)); }
Il compile ce bytecode:
0: iload_0 1: ifne 8 4: iload_1 5: iconst_1 6: iadd 7: ireturn 8: iload_1 9: ifne 20 12: iload_0 13: iconst_1 14: isub 15: iconst_1 16: invokestatic ackermann:(II)I 19: ireturn 20: iload_0 21: iconst_1 22: isub 23: iload_0 24: iload_1 25: iconst_1 26: isub 27: invokestatic ackermann:(II)I 30: invokestatic ackermann:(II)I 33: ireturn
La machine virtuelle Java (JVM), qui exécute le bytecode Java, est une machine avec une combinaison d'une pile et de registres: il y a une pile d'opérandes (STACK) dans laquelle les valeurs sont manipulées et un tableau de variables locales (LOCALS) dans lesquelles ces valeurs peuvent être stockées. La fonction démarre avec N paramètres dans les N premiers intervalles de variables locales. Lors de son exécution, la fonction déplace les données sur la pile, les opère, les replace dans des variables, appelant
return pour renvoyer la valeur à l'appelant à partir de la pile d'opérandes.
Si vous annotez le bytecode ci-dessus pour représenter les valeurs qui se déplacent entre la pile et la table de variables locale, cela ressemblera à ceci:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Ici, en utilisant
a0 et
a1 présenté les arguments de la fonction, qui sont stockés dans la table LOCALS au tout début de la fonction.
1 représente les constantes chargées via
iconst_1 , et de
v1 à
v7 , les valeurs intermédiaires calculées. Il y a trois instructions
ireturn retournant
v1 ,
v3 et
v7 . Cette fonction ne définit pas d'autres variables locales, donc le tableau LOCALS stocke uniquement les arguments d'entrée.
Ci-dessus, nous avons vu deux variantes de notre fonction -
ackermannA et
ackermannB . Ils regardent donc en bytecode:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_1 |a0|a1| |a1| 1: istore_2 |a0|a1|a1| | 2: iload_0 |a0|a1|a1| |a0| 3: istore_3 |a0|a1|a1|a0| | 4: iload_3 |a0|a1|a1|a0| |a0| 5: ifne 12 |a0|a1|a1|a0| | 8: iload_2 |a0|a1|a1|a0| |a1| 9: iconst_1 |a0|a1|a1|a0| |a1| 1| 10: iadd |a0|a1|a1|a0| |v1| 11: ireturn |a0|a1|a1|a0| | 12: iload_2 |a0|a1|a1|a0| |a1| 13: ifne 24 |a0|a1|a1|a0| | 16: iload_3 |a0|a1|a1|a0| |a0| 17: iconst_1 |a0|a1|a1|a0| |a0| 1| 18: isub |a0|a1|a1|a0| |v2| 19: iconst_1 |a0|a1|a1|a0| |v2| 1| 20: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v3| 23: ireturn |a0|a1|a1|a0| | 24: iload_3 |a0|a1|a1|a0| |a0| 25: iconst_1 |a0|a1|a1|a0| |a0| 1| 26: isub |a0|a1|a1|a0| |v4| 27: iload_3 |a0|a1|a1|a0| |v4|a0| 28: iload_2 |a0|a1|a1|a0| |v4|a0|a1| 29: iconst_1 |a0|a1|a1|a0| |v4|a0|a1| 1| 30: isub |a0|a1|a1|a0| |v4|a0|v5| 31: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v4|v6| 34: invokestatic ackermannA:(II)I |a0|a1|a1|a0| |v7| 37: ireturn |a0|a1|a1|a0| |
Étant donné que le code source prend deux arguments et les place dans des variables locales, le bytecode a les instructions correspondantes pour charger les valeurs d'argument à partir des index LOCAL 0 et 1 et les enregistrer sous les index 2 et 3. Cependant, le bytecode n'est pas intéressé par les noms de vos variables locales: il fonctionne avec par eux exclusivement comme avec les index du tableau LOCALS. Par conséquent,
ackermannA et
ackermannB auront des sous-
ackermannB identiques. C'est logique, car ils sont sémantiquement équivalents!
Cependant,
ackermannA et
ackermannB ne sont pas compilés dans le même bytecode que l'
ackermann origine: bien que le bytecode soit extrait des noms des variables locales, il n'écarte toujours pas complètement le chargement et l'enregistrement vers / depuis ces variables. Il est toujours important pour nous de savoir comment les valeurs se déplacent le long de LOCALS et STACK, bien qu'elles n'affectent pas le comportement réel du programme.
En plus de l'absence d'abstraction du chargement / enregistrement, le bytecode a un autre inconvénient: comme la plupart des assembleurs linéaires, il est très optimisé en termes de compacité, et il peut être très difficile de le modifier lorsqu'il s'agit d'optimisations.
Pour le rendre plus clair, regardons le bytecode de la fonction
ackermann originale:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | 20: iload_0 |a0|a1| |a0| 21: iconst_1 |a0|a1| |a0| 1| 22: isub |a0|a1| |v4| 23: iload_0 |a0|a1| |v4|a0| 24: iload_1 |a0|a1| |v4|a0|a1| 25: iconst_1 |a0|a1| |v4|a0|a1| 1| 26: isub |a0|a1| |v4|a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v4|v6| 30: invokestatic ackermann:(II)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Faisons un changement approximatif: que la fonction appelle
30: invokestatic ackermann:(II)I n'utilise pas son premier argument. Et puis cet appel peut être remplacé par l'appel équivalent
30: invokestatic ackermann2:(I)I , qui ne prend qu'un seul argument. Il s'agit d'une optimisation courante, qui permet d'utiliser la «suppression de code mort» pour jeter tout code utilisé pour calculer le premier argument
30: invokestatic ackermann:(II)IPour ce faire, nous devons non seulement remplacer l'instruction
30 , mais également regarder la liste des instructions et comprendre où le premier argument est calculé (
v4 dans
STACK ), et aussi le supprimer. Nous revenons des instructions
30 à
22 , et des
22 à
21 et
20 . La version finale:
BYTECODE LOCALS STACK |a0|a1| | 0: iload_0 |a0|a1| |a0| 1: ifne 8 |a0|a1| | 4: iload_1 |a0|a1| |a1| 5: iconst_1 |a0|a1| |a1| 1| 6: iadd |a0|a1| |v1| 7: ireturn |a0|a1| | 8: iload_1 |a0|a1| |a1| 9: ifne 20 |a0|a1| | 12: iload_0 |a0|a1| |a0| 13: iconst_1 |a0|a1| |a0| 1| 14: isub |a0|a1| |v2| 15: iconst_1 |a0|a1| |v2| 1| 16: invokestatic ackermann:(II)I |a0|a1| |v3| 19: ireturn |a0|a1| | - 20: iload_0 |a0|a1| | - 21: iconst_1 |a0|a1| | - 22: isub |a0|a1| | 23: iload_0 |a0|a1| |a0| 24: iload_1 |a0|a1| |a0|a1| 25: iconst_1 |a0|a1| |a0|a1| 1| 26: isub |a0|a1| |a0|v5| 27: invokestatic ackermann:(II)I |a0|a1| |v6| - 30: invokestatic ackermann:(II)I |a0|a1| |v7| + 30: invokestatic ackermann2:(I)I |a0|a1| |v7| 33: ireturn |a0|a1| |
Nous pouvons toujours apporter une modification aussi simple à une simple fonction
ackermann . Mais dans les grandes fonctions utilisées dans les projets réels, il sera beaucoup plus difficile d'effectuer de nombreux changements interconnectés. En général, toute petite modification sémantique de votre programme peut nécessiter de nombreuses modifications tout au long du bytecode.
Vous remarquerez peut-être que nous avons effectué le changement décrit ci-dessus en analysant les valeurs dans LOCALS et STACK: nous avons observé comment
v4 passé à l'instruction
30 de l'instruction
22 , et
22 prend les données à
a0 et
1 , qui proviennent des instructions
21 et
20 . Ces valeurs sont transférées entre LOCALS et STACK selon le principe du graphe: de l'instruction calculant la valeur au lieu de son utilisation ultérieure.
Comme les paires
Ident /
Assign dans nos AST, les valeurs transmises entre LOCALS et STACK forment un graphique entre les points qui calculent les valeurs et les points qui sont utilisés. Alors pourquoi ne commençons-nous pas à travailler directement avec le graphique?
Graphiques de flux de données
Les graphiques de flux de données sont le prochain niveau d'abstraction après le bytecode. Si nous développons notre arbre de syntaxe avec des relations
Ident /
Assign , ou si nous suivons comment le bytecode déplace les valeurs entre LOCALS et STACK, nous pouvons construire un graphique. Pour la fonction
ackermann cela ressemble à ceci:

Contrairement au bytecode AST ou Java stack-bytecode, les graphiques de flux de données n'utilisent pas le concept de «variable locale»: au lieu de cela, le graphique contient des connexions directes entre chaque valeur et l'endroit où elle est utilisée. Lors de l'analyse du bytecode, il est souvent nécessaire d'interpréter de manière abstraite LOCALS et STACK afin de comprendre comment les valeurs se déplacent; L'analyse AST implique le suivi de l'arbre et l'utilisation d'une table de symboles contenant les associations
Assign /
Ident ; et l'analyse des graphiques de flux de données est souvent un suivi direct des transitions - l'idée pure de «valeurs en mouvement» sans les enveloppes de la présentation d'un programme.
ackermann également plus faciles à manipuler que le bytecode linéaire: remplacer un nœud par un appel
ackermann appel
ackermann et
ackermann2 un des arguments revient simplement à modifier le nœud du graphique (marqué en vert) et à supprimer l'un des liens d'entrée avec les nœuds de transit (marqués en rouge):

Comme vous pouvez le voir, un petit changement dans le programme (en remplaçant
ackermann(int n, int m) par
ackermann2(int m) ) se transforme en un changement relativement localisé dans le graphique du flux de données.
En général, travailler avec des graphiques est beaucoup plus facile qu'avec un bytecode linéaire ou AST: ils sont faciles à analyser et à modifier.
Il n'y a pas beaucoup de détails dans cette description des graphiques: en plus de la représentation physique réelle du graphique, il existe de nombreuses autres façons de modéliser l'état et le contrôle de flux, qui sont plus difficiles à travailler avec et au-delà de la portée de l'article. J'ai également omis un certain nombre de détails sur la transformation de graphiques, par exemple, l'ajout et la suppression de liens, les transitions avant et arrière, les transitions horizontales et verticales (en largeur et en profondeur), etc. Si vous avez étudié les algorithmes, tout cela devrait vous être familier .
Enfin, nous avons omis les algorithmes de conversion du bytecode linéaire en graphique, puis du graphique en retour en bytecode. C'est en soi une tâche intéressante, mais nous vous laissons le soin d'étudier de manière indépendante.
Analyse
Après avoir eu l'idée du programme, nous devons l'analyser: découvrez quelques faits qui vous permettront de transformer le programme sans changer son comportement. Bon nombre des optimisations discutées ci-dessus sont basées sur l'analyse du programme:
- Pliage constant: le résultat de l'expression fonctionne-t-il avec une valeur constante connue? Le calcul de l'expression est-il pur?
- Casting et inlining de type: un appel de méthode est-il un type avec une seule implémentation de la méthode appelée?
- : ?
- : «»? - ? ?
- : , ?
, , , . , , , .
, , , — , . .
(Inference Lattice)
, . , «» - :
Integer ? String ? Array[Float] ? PrintLogger ?
CharSequence ? String , - StringBuilder ?
Any , , ?
:

: ,
"hello" String ,
String CharSequence .
"hello" , (Singleton Type) — . :

, , . , . , , ,
String StringBuilder , , :
CharSequence . ,
0 ,
1 ,
2 , ,
Integer .

, , :

, , . , .
count
main :
static int main(int n){ int count = 0, multiplied = 0; while(count < n){ if (multiplied < 100) logger.log(count); count += 1; multiplied *= count; } return ...; }
ackermann ,
count ,
multiplied logger . :

,
count 0 block0 .
block1 , ,
count < n : ,
block3 return ,
block2 ,
count 1 count ,
block1 . ,
< false ,
block3 .
?
block0 . , count = 0.
block1 , , n ( , Integer ), , if . block2 block3.block3 , , block1b , block2 , , block1c . , block2 count , 1 count.- ,
count 0 1 : count Integer. - :
block1 n count Integer .
block2 , count Integer + 1 -> Integer . , count Integer , .
multiplied
,
multiplied :
block0 . , multiplied 0.
block1 , , . block2 block3 ( ).
block2 , block2 ( 0 ) count ( Integer ). 0 * Integer -> 0 , multiplied 0.
block1 block2 . multiplied 0 , .
multiplied 0 , , :
multiplied < 100 true.
if (multiplied < 100) logger.log(count); logger.log(count) .
- ,
multiplied , , 0 .
:

:

:
static int main(int n){ int count = 0; while(count < n){ logger.log(count); count += 1; } return ...; }
, , , , .
multiplied -> 0 , , . , , . , .
, . :
count ,
multiplied . ,
multiplied count ,
count multiplied . , .
, — : , . , ( ) . .
while , ,
O( ) . (, ) , , .
, .
, . , , , , .
. :
static int main(int n){ return called(n, 0); } static int called(int x, int y){ return x * y; }
:

main :
main(n)
called(n, 0)
called(n, 0) 0
main(n) 0
, , . .
,
called(n, 0) 0 , :

:
static int main(int n){ return 0; }
: A B, C, D, D C, B, D A. A B B A, A A, , !
, Java:
public static Any factorial(int n) { if (n == 1) { return 1; } else { return n * factorial(n - 1); } }
n int ,
Any : . ,
factorial int (
Integer ).
factorial ,
factorial factorial , ! ?
Bottom
Bottom :

« , , ».
Bottom factorial :

block0 . n Integer , 1 1 , n == 1 , true false .
true : return 1 .
false n - 1 n Integer .
factorial — , Bottom .
* n: Integer factorial : Bottom Bottom .
return Bottom .factorial 1 Bottom , 1 .
1 factorial , Bottom .
Integer * 1 Integer .
return Integer .factorial Integer 1 , Integer .
factorial , Integer . * n: Integer factorial: Integer , Integer , .
factorial Integer , , .
, .
Bottom , , .
* :
(n: Integer) * (factorial: Bottom)
(n: Integer) * (factorial: 1)
(n: Integer) * (factorial: Integer)
multiplied ,
O( ) . , , .
— , « ». , (« »), , (« »). .
main :
static int main(int n){ int count = 0, total = 0, multiplied = 0; while(count < n){ if (multiplied > 100) count += 1; count += 1; multiplied *= 2; total += 1; } return count; }
,
if (multiplied > 100) multiplied *= count multiplied *= 2 . .
, :
multiplied > 100 true , count += 1 («»).
total , («»).
, :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
, .
:

, , :
block0 ,
block1 , ,
block1b , ,
block1c , ,
return block3 .
,
multiplied -> 0 , :

:

,
block1b (
0 > 100 )
true .
false block1c (
if ):
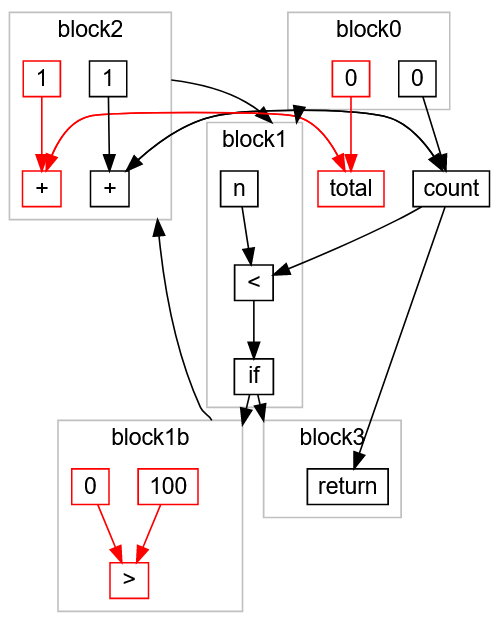
, « »
total > , - , , . ,
return ,
:
> ,
100 ,
0 block1b ,
total ,
0 ,
+ 1 ,
total block0 block2 . :

«» :
static int main(int n){ int count = 0; while(count < n){ count += 1; } return count; }
Conclusion
:
- -.
- , .
- , . .
- : «» «» , , .
- : , .
- , .
, , .
, . . , :