Je continue à publier mes conférences, à l'origine destinées aux étudiants étudiant dans la spécialité de "géologie numérique". Il s'agit de la troisième publication du cycle du hub, le premier article était une introduction, il n'est pas nécessaire de le lire. Cependant, pour comprendre cet article, il est nécessaire de lire l' introduction aux systèmes linéaires d'équations même si vous savez ce que c'est, car je me référerai beaucoup aux exemples de cette introduction.

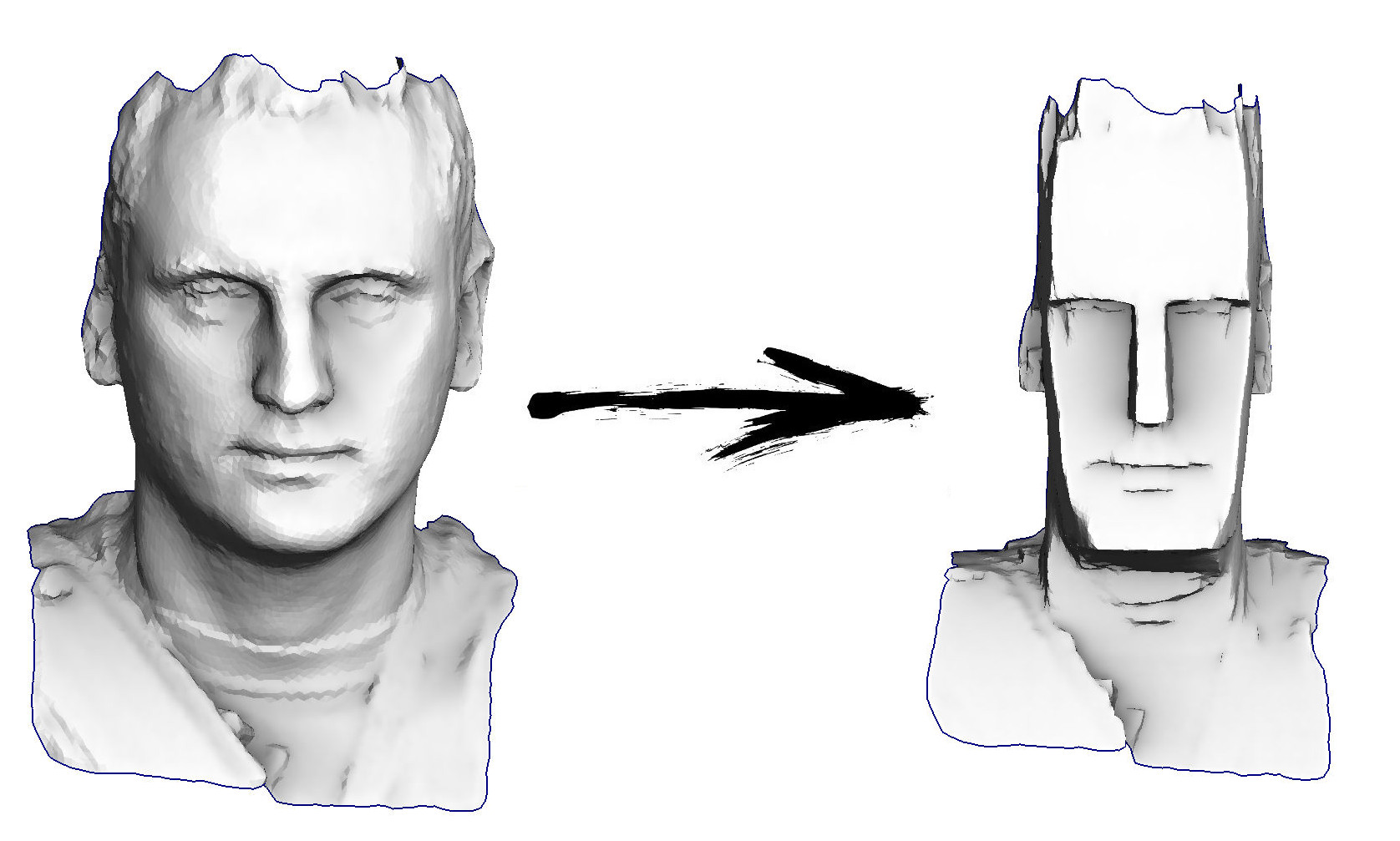
Alors, la tâche pour aujourd'hui: apprendre le traitement de géométrie le plus simple, par exemple, pour pouvoir transformer ma tête en une idole de l'île de Pâques:



Plan de cours actuel:

• Programme éducatif sur la théorie des probabilités (article introductif, facultatif)
  
• Introduction aux systèmes linéaires d'équations
  
• Minimisation des formes quadratiques et exemples de problèmes OLS
  
• Des moindres carrés aux réseaux de neurones
  

Le référentiel de cours officiel vit ici . Le livre n'est pas encore terminé, je compile lentement des articles publiés sur Habré.

Dans cet article, mon principal outil sera de trouver le minimum de fonctions quadratiques; mais avant de commencer à utiliser cet outil, vous devez au moins comprendre où il a le bouton marche / arrêt. Tout d'abord, rafraîchissez la mémoire et rappelez-vous ce que sont les matrices, ce qu'est un nombre positif et aussi ce qu'est un dérivé.

Matrices et nombres

Dans ce texte, j'utiliserai abondamment la notation matricielle, alors rappelons-nous ce que c'est. Ne cherchez pas plus loin dans le texte, ne vous arrêtez pas quelques secondes et essayez de formuler ce qu'est une matrice.

Différentes interprétations matricielles

La réponse est très simple. La matrice est juste une armoire dans laquelle le raifort est stocké. Chaque merde se trouve dans sa cellule, les cellules sont regroupées en lignes en lignes et en colonnes. Dans notre cas particulier, les nombres réels habituels sont de la merde; il est plus facile pour un programmeur de présenter une matrice $$$A$ comme quelque chose

float A[m][n]; 

Pourquoi ces stockages sont-ils nécessaires? Que décrivent-ils? Je vais peut-être vous contrarier, mais la matrice elle-même ne décrit rien, elle stocke. Par exemple, vous pouvez y stocker les coefficients de toutes les fonctions. Oublions les matrices pendant une seconde, et imaginons que nous avons un certain nombre $$$a$ . Qu'est-ce que cela signifie? Oui, le diable sait ... Par exemple, il peut s'agir d'un coefficient à l'intérieur d'une fonction qui prend un nombre en entrée et donne un autre nombre en sortie:

$$

$$f (x): \ mathbb R \ rightarrow \ mathbb R$$

Un mathématicien pourrait écrire une version d'une telle fonction comme

$$

$$f (x) = ax$$

Eh bien, dans le monde des programmeurs, cela ressemblerait à ceci:

 float f(float x) { return a*x; } 

D'un autre côté, pourquoi une telle fonction, et pas tout à fait une autre? Prenons un autre!

$$

$$f (x) = ax ^ 2$$

Depuis que j'ai commencé sur les programmeurs, je dois écrire son code :)

 float f(float x) { return x*a*x; } 

L'une de ces fonctions est linéaire et la seconde est quadratique. Laquelle est correcte? Non, le numéro lui-même $$$a$ ne le définit pas, il stocke juste une certaine valeur! De quelle fonction avez-vous besoin, construisez-en une comme ça.

La même chose se produit avec les matrices, ce sont des stockages nécessaires au cas où il n'y aurait pas assez de nombres simples (scalaires), une sorte d'expansion des nombres. Au-dessus des matrices, tout comme au-dessus des nombres, les opérations d'addition et de multiplication sont définies.

Imaginons que nous ayons une matrice $$$A$ Par exemple, taille 2x2:

$$

$$A = \ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix}$$

Cette matrice en soi ne signifie rien, par exemple, elle peut être interprétée comme une fonction

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2, \ quad f (x) = Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

Cette fonction convertit un vecteur bidimensionnel en un vecteur bidimensionnel. Graphiquement, il est pratique de présenter cela comme une conversion d'image: nous donnons l'image à l'entrée, et à la sortie nous obtenons sa version étirée et / ou pivotée (peut-être même en miroir!). Très prochainement, je donnerai une image avec divers exemples d'une telle interprétation des matrices.

Et la matrice peut-elle $$$A$ imaginez comme une fonction qui convertit un vecteur à deux dimensions en un scalaire:

$$

$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R, \ quad f (x) = x ^ \ top A x = \ sum \ limits_i \ sum \ limits_j a_ {ij} x_i x_j$$

Notez que l'exponentiation n'est pas très définie avec des vecteurs, donc je ne peux pas écrire $$$x ^ 2$ , comme il l'a écrit dans le cas des nombres ordinaires. Je recommande fortement à ceux qui n'ont pas l'habitude de jongler facilement avec les multiplications matricielles, de rappeler une fois de plus la règle de multiplication matricielle et de vérifier que l'expression $$$x ^ \ top A x$ généralement autorisé et donne vraiment un scalaire à la sortie. Pour ce faire, par exemple, vous pouvez mettre explicitement des crochets $$$x ^ \ top A x = (x ^ \ top A) x$ . Je vous rappelle que nous avons $$$x$ Est un vecteur de dimension 2 (stocké dans une matrice de dimension 2x1), nous écrivons explicitement toutes les dimensions:

$$

$$\ underbrace {\ underbrace {\ left (\ underbrace {x ^ \ top} _ {1 \ times 2} \ times \ underbrace {A} _ {2 \ times 2} \ right)} _ {1 \ times 2} \ times \ underbrace {x} _ {2 \ times 1}} _ {1 \ times 1}$$

Revenant au monde chaleureux et moelleux des programmeurs, nous pouvons écrire la même fonction quadratique quelque chose comme ceci:

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

Qu'est-ce qu'un nombre positif?

Maintenant, je vais poser une question très stupide: qu'est-ce qu'un nombre positif? Nous avons plus un excellent outil appelé prédicat $$$>$ . Mais prenez votre temps pour répondre à ce numéro $$$a$ positif si et seulement si $$$a> 0$ Ce serait trop facile. Définissons la positivité comme suit:

Définition 1

Numéro $$$a$ positif si et seulement si pour tout réel non nul $$$x \ in \ mathbb R, \ x \ neq 0$ la condition est remplie $$$ax ^ 2> 0$ .

Cela semble assez délicat, mais cela s'applique parfaitement aux matrices:

Définition 2

Matrice carrée $$$A$ est appelé positif défini si, pour tout non différent de zéro $$$x$ la condition est remplie $$$x ^ \ top A x> 0$ c'est-à-dire que la forme quadratique correspondante est strictement positive partout sauf pour l'origine.

Pourquoi ai-je besoin de positivité? Comme je l'ai mentionné au début de l'article, mon principal outil sera de rechercher les minimums de fonctions quadratiques. Mais pour au moins chercher, ce ne serait pas mal si ça existait! Par exemple, une fonction $$$f (x) = - x ^ 2$ le minimum n'existe évidemment pas, puisque le nombre -1 n'est pas positif, et $$$f (x)$ diminue sans cesse avec la croissance $$$x$ : branches d'une parabole $$$f (x)$ regarde en bas. Les matrices définies positives sont bonnes en ce que les formes quadratiques correspondantes forment un paraboloïde ayant un minimum (unique). L'illustration suivante montre sept exemples différents de matrices. $$$2 \ fois 2$ , à la fois positive définie et symétrique, et non. Rangée supérieure: interprétation des matrices en tant que fonctions $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ . Rangée du milieu: interprétation des matrices comme fonctions $$$f (x): \ mathbb R ^ 2 \ rightarrow \ mathbb R$ .



Ainsi, je travaillerai avec des matrices définies positives, qui sont une généralisation de nombres positifs. De plus, spécifiquement dans mon cas, les matrices seront également symétriques! Il est curieux que, bien souvent, lorsque les gens parlent de certitude positive, ils impliquent également une symétrie, qui peut être indirectement expliquée par l'observation suivante (facultative pour comprendre le texte suivant).

Digression lyrique sur la symétrie des matrices de formes quadratiques

Regardons la forme quadratique $$$x ^ \ top M x$ pour une matrice arbitraire $$$M$ ; puis $$$M$ ajouter et soustraire immédiatement la moitié de sa version transposée:

$$

$$M = \ underbrace {\ frac {1} {2} (M + M ^ \ top)} _ {: = M_s} + \ underbrace {\ frac {1} {2} (MM ^ \ top)} _ { : = M_a} = M_s + M_a$$

Matrix $$$M_s$ symétrique: $$$M_s ^ \ top = M_s$ ; matrice $$$M_a$ antisymétrique: $$$M_a ^ \ top = -M_a$ . Un fait remarquable est que pour toute matrice antisymétrique, la forme quadratique correspondante est identiquement égale à zéro. Cela découle de l'observation suivante:

$$

$$q = x ^ \ top M_a x = (x ^ \ top M_a ^ \ top x) ^ \ top = - (x ^ \ top M_a x) ^ \ top = -q$$

Autrement dit, la forme quadratique $$$x ^ \ top M_a x$ simultanément égal $$$q$ et $$$-q$ , ce qui n'est possible que lorsque $$$q \ equiv 0$ . De ce fait, il résulte que pour une matrice arbitraire $$$M$ forme quadratique correspondante $$$x ^ \ top M x$ peut être exprimé à travers une matrice symétrique $$$M_s$ :

$$

$$x ^ \ top M x = x ^ \ top (M_s + M_a) x = x ^ \ top M_s x + x ^ \ top M_a x = x ^ \ top M_s x.$$

Nous recherchons un minimum d'une fonction quadratique

Revenons brièvement au monde unidimensionnel; Je veux trouver un minimum de fonction $$$f (x) = ax ^ 2 - 2bx$ . Numéro $$$a$ positivement, donc un minimum existe; pour le trouver, on met à zéro la dérivée correspondante: $$$\ frac {d} {dx} f (x) = 0$ . Différencier la fonction quadratique unidimensionnelle du travail n'est pas: $$$\ frac {d} {dx} f (x) = 2ax - 2b = 0$ ; donc notre problème se résume à résoudre l'équation $$$ax-b = 0$ , où, grâce à des efforts terribles, nous obtenons une solution $$$x ^ * = b / a$ . La figure suivante illustre l'équivalence de deux problèmes: solution $$$x ^ *$ équations $$$ax-b = 0$ coïncide avec la solution de l'équation $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ .



J'ai tendance à dire que notre objectif global est de minimiser les fonctions quadratiques, mais nous parlons des moindres carrés. Mais en même temps, ce que nous savons vraiment faire, c'est de résoudre des équations linéaires (et des systèmes d'équations linéaires). Et c'est très cool que l'un soit équivalent à l'autre!

Il ne nous reste plus qu'à nous assurer que cette équivalence dans le monde unidimensionnel s'étend au cas $$$n$ variables. Pour vérifier cela, nous prouvons d'abord trois théorèmes.

Trois théorèmes, ou différencier les expressions matricielles

Le premier théorème déclare que les matrices $$$1 \ fois 1$ invariants par rapport à la transposition:

Théorème 1

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

La preuve est si compliquée que je dois l'omettre par souci de concision, mais essayez de la trouver vous-même.

Le deuxième théorème nous permet de différencier les fonctions linéaires. Dans le cas d'une fonction réelle d'une variable, nous savons que $$$\ frac {d} {dx} (bx) = b$ mais ce qui se passe dans le cas d'une fonction réelle $$$n$ variables?

Théorème 2

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

Autrement dit, pas de surprise, juste un enregistrement matriciel du même résultat scolaire. La preuve est extrêmement simple, il suffit d'écrire la définition du gradient:

$$

$$\ nabla (b ^ \ top x) = \ begin {bmatrix} \ frac {\ partial (b ^ \ top x)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (b ^ \ top x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ frac {\ partial (b_1 x_1 + \ dots + b_n x_n)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partiel (b_1 x_1 + \ dots + b_n x_n)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} b_1 \\ \ vdots \\ b_n \ end {bmatrix} = b$$

Application du premier théorème $$$b ^ \ top x = x ^ \ top b$ , nous complétons la preuve.

Passons maintenant aux formes quadratiques. On sait que dans le cas d'une fonction réelle d'une variable $$$\ frac {d} {dx} (ax ^ 2) = 2ax$ , et que se passera-t-il dans le cas d'une forme quadratique?

Théorème 3

$$$\ nabla (x ^ \ top A x) = (A + A ^ \ top) x$

Soit dit en passant, si la matrice $$$A$ symétrique, le théorème dit que $$$\ nabla (x ^ \ top A x) = 2Ax$ .

Cette preuve est également simple, il suffit d'écrire la forme quadratique comme une double somme:

$$

$$x ^ \ top A x = \ sum \ limits_i \ sum \ limits_j a_ {ij} x_i x_j$$

Et puis voyons quelle est la dérivée partielle de cette double somme par rapport à la variable $$$x_i$ :
\ begin {align *}
\ frac {\ partial (x ^ \ top A x)} {\ partial x_i}
& = \ frac {\ partial} {\ partial x_i} \ left (\ sum \ limits_ {k_1} \ sum \ limits_ {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} \ right) = \\
& = \ frac {\ partial} {\ partial x_i} \ left (
\ underbrace {\ sum \ limits_ {k_1 \ neq i} \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ {k_1 \ neq i, k_2 \ neq i} + \ underbrace {\ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i, k_2 \ neq i} +
\ underbrace {\ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i, k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i, k_2 = i} \ right) = \\
& = \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} + 2 a_ {ii} x_i = \\
& = \ sum \ limits_ {k_2} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1} a_ {k_1 i} x_ {k_1} = \\
& = \ sum \ limits_ {j} (a_ {ij} + a_ {ji}) x_j \\
\ end {align *}
J'ai divisé la double somme en quatre cas, qui sont mis en évidence par des accolades. Chacun de ces quatre cas se différencie trivialement. Reste à faire la dernière action, collecter les dérivées partielles dans le vecteur gradient:

$$

$$\ nabla (x ^ \ top A x) = \ begin {bmatrix} \ frac {\ partial (x ^ \ top Ax)} {\ partial x_1} \\ \ vdots \\ \ frac {\ partial (x ^ \ top A x)} {\ partial x_n} \ end {bmatrix} = \ begin {bmatrix} \ sum \ limits_ {j} (a_ {1j} + a_ {j1}) x_j \\ \ vdots \\ \ sum \ limits_ {j} (a_ {nj} + a_ {jn}) x_j \ end {bmatrix} = (A + A ^ \ top) x$$

Le minimum de la fonction quadratique et la solution du système linéaire

N'oublions pas le sens de la marche. Nous avons vu cela avec un nombre positif $$$a$ dans le cas de fonctions réelles d'une variable, résoudre l'équation $$$ax = b$ ou minimiser la fonction quadratique $$$\ mathrm {argmin} _x (ax ^ 2 - 2bx)$ Sont une seule et même chose.

Nous voulons montrer la connexion correspondante dans le cas d'une matrice définie positive symétrique $$$A$ .
Nous voulons donc trouver le minimum de la fonction quadratique

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n} (x ^ \ top A x - 2b ^ \ top x).$$

Exactement comme à l'école, on assimile la dérivée à zéro:

$$

$$\ nabla (x ^ \ top A x - 2b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}.$$

L'opérateur de Hamilton est linéaire, nous pouvons donc réécrire notre équation sous la forme suivante:

$$

$$\ nabla (x ^ \ top A x) - 2 \ nabla (b ^ \ top x) = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Maintenant, nous appliquons les deuxième et troisième théorèmes de différenciation:

$$

$$(A + A ^ \ top) x - 2b = \ begin {bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Rappelez-vous que $$$A$ symétrique, et diviser l'équation en deux, nous obtenons le système d'équations linéaires dont nous avons besoin:

$$

$$Ax = b$$

Hourra, en passant d'une variable à plusieurs, nous n'avons rien perdu du tout, et nous pouvons efficacement minimiser les fonctions quadratiques!

On passe aux moindres carrés

Enfin, nous pouvons passer au contenu principal de cette conférence. Imaginez que nous ayons deux points sur un avion $$$(x_1, y_1)$ et $$$(x_2, y_2)$ , et nous voulons trouver l'équation d'une ligne passant par ces deux points. L'équation de la ligne peut s'écrire $$$y = \ alpha x + \ beta$ c'est-à-dire que notre tâche consiste à trouver les coefficients $$$\ alpha$ et $$$\ beta$ . Cet exercice concerne la septième-huitième année de l'école, nous notons le système d'équations:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ end {split} \ right.$$

Nous avons deux équations avec deux inconnues ( $$$\ alpha$ et $$$\ beta$ ), le reste est connu.

Dans le cas général, une solution existe et est unique. Pour plus de commodité, nous réécrivons le même système sous forme matricielle:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \ end {bmatrix}} _ {: = A} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \ end {bmatrix}} _ {: = b}$$

On obtient une équation de type $$$Ax = b$ qui est trivialement résolu $$$x ^ * = A ^ {- 1} b$ .

Imaginez maintenant que nous avons trois points à travers lesquels nous devons tracer une ligne droite:

$$

$$\ left \ {\ begin {split} \ alpha x_1 + \ beta & = y_1 \\ \ alpha x_2 + \ beta & = y_2 \\ \ alpha x_3 + \ beta & = y_3 \\ \ end {split} \ right .$$

Sous forme matricielle, ce système s'écrit comme suit:

$$

$$\ underbrace {\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix}} _ {: = A \, (3 \ times 2)} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {: = x \, (2 \ fois 1)} = \ underbrace {\ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}} _ { : = b \, (3 \ fois 1)}$$

Maintenant, nous avons une matrice $$$A$ rectangulaire, et il n'existe tout simplement pas inversé! C'est tout à fait normal, car nous n'avons que deux variables et trois équations, et dans le cas général, ce système n'a pas de solution. Il s'agit d'une situation tout à fait normale dans le monde réel, lorsque les points sont des données de mesures bruyantes, et nous devons trouver les paramètres $$$\ alpha$ et $$$\ beta$ que les meilleures données de mesure approximatives . Nous avons déjà considéré cet exemple lors de la première conférence, lorsque le steelyard étalonné. Mais alors notre solution était purement algébrique et très lourde. Essayons une manière plus intuitive.

Notre système peut s'écrire comme suit:

$$

$$\ alpha \ underbrace {\ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ {: = \ vec {i}} + \ beta \ underbrace {\ begin {bmatrix} 1 \\ 1 \ \ 1 \ end {bmatrix}} _ {: = \ vec {j}} = \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}$$

Ou, plus brièvement,

$$

$$\ alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}.$$

Vecteurs $$$\ vec i$ , $$$\ vec j$ et $$$\ vec b$ connu, besoin de trouver des scalaires $$$\ alpha$ et $$$\ beta$ .
Combinaison évidemment linéaire $$$\ alpha \ vec {i} + \ beta \ vec {j}$ engendre un avion, et si le vecteur $$$\ vec b$ ne réside pas dans ce plan, alors il n'y a pas de solution exacte; cependant, nous recherchons une solution approximative.

Définissons l'erreur de décision comme $$$\ vec {e} (\ alpha, \ beta): = \ alpha \ vec {i} + \ beta \ vec {j} - \ vec b$ . Notre objectif est de trouver de telles valeurs de paramètres $$$\ alpha$ et $$$\ beta$ qui minimisent la longueur du vecteur $$$\ vec {e} (\ alpha, \ beta)$ . En d'autres termes, le problème est écrit comme $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ .
En voici une illustration:.



Ayant donné des vecteurs $$$\ vec i$ , $$$\ vec j$ et $$$\ vec b$ , nous essayons de minimiser la longueur du vecteur d'erreur $$$\ vec e$ . Evidemment, sa longueur est minimisée si elle est perpendiculaire au plan étiré sur les vecteurs $$$\ vec i$ et $$$\ vec j$ .

Mais attendez, où sont les moindres carrés? Maintenant, ils le seront. Fonction d'extraction de racine $$$\ sqrt {\ cdot}$ monotone donc $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ |$ = $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ !

Il est bien évident que la longueur du vecteur d'erreur est minimisée si elle est perpendiculaire au plan étiré sur les vecteurs $$$\ vec i$ et $$$\ vec j$ , qui peut s'écrire en mettant à zéro les produits scalaires correspondants:

$$

$$\ left \ {\ begin {split} \ vec {i} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \\ \ vec {j} ^ \ top \ vec {e} (\ alpha, \ beta) & = 0 \ end {split} \ right.$$

Sous forme matricielle, ce même système peut s'écrire

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ alpha \ begin {bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix} + \ beta \ begin {bmatrix} 1 \\ 1 \\ 1 \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix }$$

ou bien

$$

$$\ begin {bmatrix} x_1 & x_2 & x_3 \\ 1 & 1 & 1 \ end {bmatrix} \ left (\ begin {bmatrix} x_1 & 1 \\ x_2 & 1 \\ x_3 & 1 \ end {bmatrix} \ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix} - \ begin {bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix} }$$

Mais nous ne nous arrêterons pas là, car le record peut être encore réduit:

$$

$$A ^ \ top (Axe - b) = \ begin {bmatrix} 0 \\ 0 \ end {bmatrix}$$

Et la transformation la plus récente:

$$

$$A ^ \ top Ax = A ^ \ top b.$$

Calculons les dimensions. Matrix $$$A$ a la taille $$$3 \ fois 2$ donc $$$A ^ \ top A$ a la taille $$$2 \ fois 2$ . Matrix $$$b$ a la taille $$$3 \ fois 1$ mais vecteur $$$A ^ \ top b$ a la taille $$$2 \ fois 1$ . Soit, dans le cas général, la matrice $$$A ^ \ top A$ réversible! De plus, $$$A ^ \ top A$ Il a quelques belles propriétés.

Théorème 4

$$$A ^ \ top A$ symétrique.

Ce n'est pas du tout difficile à montrer:

$$

$$(A ^ \ top A) ^ \ top = A ^ \ top (A ^ \ top) ^ \ top = A ^ \ top A.$$

Théorème 5

$$$A ^ \ top A$ positivement semi-défini: $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geq 0.$

Cela découle du fait que $$$x ^ \ top A ^ \ top A x = (A x) ^ \ top A x> 0$ .

Aussi $$$A ^ \ top A$ positif défini si $$$A$ a des colonnes linéairement indépendantes (rang $$$A$ égal au nombre de variables du système).

Au total, pour un système à deux inconnues, nous avons prouvé que la minimisation d'une fonction quadratique $$$\ mathrm {argmin} _ {\ alpha, \ beta} \ | \ vec {e} (\ alpha, \ beta) \ | ^ 2$ équivalent à résoudre un système d'équations linéaires $$$A ^ \ top A x = A ^ \ top b$ . Bien sûr, tout ce raisonnement s'applique à tout autre nombre de variables, mais réécrivons tout de manière compacte avec un simple calcul algébrique. Nous commençons par le problème des moindres carrés, arrivons à la minimisation de la fonction quadratique de la forme familière, et de là nous concluons qu'il équivaut à résoudre un système d'équations linéaires. Alors allons-y:

$$

$$\ begin {split} \ mathrm {argmin} \ | Axe - b \ | ^ 2 & = \ mathrm {argmin} (Axe-b) ^ \ top (Axe-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top - b ^ \ top) (Ax-b) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - b ^ \ top Ax - x ^ \ top A ^ \ top b + \ underbrace {b ^ \ top b} _ {\ rm const}) = \\ & = \ mathrm {argmin} (x ^ \ top A ^ \ top A x - 2b ^ \ top Ax) = \\ & = \ mathrm {argmin} ( x ^ \ top \ underbrace {(A ^ \ top A)} _ {: = A '} x - 2 \ underbrace {(A ^ \ top b)} _ {: = b'} \ phantom {} ^ \ top x) \ end {split}$$

Donc le problème des moindres carrés $$$\ mathrm {argmin} \ | Hache - b \ | ^ 2$ équivalent à minimiser une fonction quadratique $$$\ mathrm {argmin} (x ^ \ top A 'x - 2b' ^ \ top x)$ avec (dans le cas général) une matrice définie positive symétrique $$$A '$ , ce qui, à son tour, équivaut à résoudre un système d'équations linéaires $$$A'x = b '$ . Uff. La théorie est terminée.

Passons à la pratique

Exemple un, unidimensionnel

Rappelons un exemple d'un article précédent :

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

Nous avons un tableau x régulier de 32 éléments, initialisé comme suit:



Et puis nous effectuerons la procédure suivante mille fois: pour chaque cellule x [i], nous y écrivons la valeur moyenne des cellules voisines: x [i] = (x [i-1] + x [i + 1]) / 2. Seule exception: nous ne réécrirons pas les éléments du tableau avec les nombres 0, 18 et 31. Voici à quoi ressemble l'évolution du tableau dans les cent cinquante premières itérations:



Comme nous l'avons trouvé dans un article précédent , il s'avère que notre mégacode de code python à quatre lignes résout le système d'équations linéaires suivant par la méthode de Gauss-Seidel:



Ils l'ont découvert, mais d'où vient ce système? Quel genre de magie? Écartons-nous une seconde et essayons de résoudre un système légèrement différent. J'ai encore 32 variables, mais maintenant je veux qu'elles soient toutes égales les unes aux autres. Ce n'est pas difficile à écrire, il suffit d'écrire un système d'équations qui stipule que tous les éléments voisins sont égaux par paires:



Le code Python ci-dessus, en principe, ne touche pas les valeurs de trois variables: x0, x18, x31, alors transférons-les du côté droit du système d'équations, c'est-à-dire, excluons de l'ensemble des inconnues:



Je fixe la valeur initiale x0 = 1, la première équation dit x1 = x0 = 1, la deuxième équation dit x2 = x1 = x0 = 1 et ainsi de suite, jusqu'à arriver à l'équation 1 = x0 = x17 = x18 = 2 Oh! Mais ce système n'a pas de solution: ((

Et peu importe, nous sommes programmeurs! Appelons les moindres carrés à l'aide! Notre système insoluble peut être écrit sous forme matricielle $$$Ax = b$ ; pour résoudre notre système approximativement, il suffit de résoudre le système $$$A^\top Ax=A^\top b$ .Et puis il s'avère que c'est exactement le système d'équations un-en-un de l'article précédent!

Intuitivement, on peut imaginer le processus de création d'une matrice système comme suit: nous connectons les valeurs avec des ressorts que nous voulons atteindre l'égalité. Par exemple, dans notre cas, nous voulons$$$x_i$ était égal $$$x_{i+1}$ , nous ajoutons donc l'équation $$$x_i - x_{i+1}=0$suspendu entre ces valeurs un ressort qui les rapprochera. Mais étant donné que les valeurs de x0, x18 et x31 sont fermement fixées, il ne reste plus de valeurs libres que d'étirer les ressorts uniformément, produisant (dans ce cas) une solution linéaire par morceaux.

Écrivons un programme qui résout ce système d'équations. Dans le dernier article, nous avons vu que la méthode de Gauss-Seidel est très simple en programmation, mais a une convergence très lente, il serait donc préférable d'utiliser de vrais solveurs de systèmes d'équations linéaires. Dans le cas le plus simple, pour notre exemple unidimensionnel, le code peut ressembler à ceci:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

Ce code produit une liste x de 32 éléments dans lesquels la solution est stockée. Nous construisons une matrice$$$A$ vecteur de construction $$$b$ nous obtenons un vecteur avec une solution $$$x = (A^\top A)^{-1}A^\top b$puis nous insérons nos valeurs fixes x0 = 1, x18 = 2 et x31 = 1 dans ce vecteur.

Ce code fait le travail nécessaire, mais il est plutôt désagréable de transférer les valeurs des variables fixes vers la droite. Est-il possible de tricher? Tu peux! Regardons le code suivant:

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

Du point de vue d'un programmeur, c'est beaucoup plus agréable, le vecteur x est obtenu immédiatement de la dimension requise, et les matrices A et b sont remplies beaucoup plus facilement. Mais quel est le truc? Écrivons le système d'équations que nous résolvons:



Examinez attentivement les trois dernières équations:
100 x0 = 100 * 1
100 x18 = 100 * 2
100 x31 = 100 * 1

Serait-il plus facile de les écrire comme suit?
x0 = 1
x18 = 2
x31 = 1

Non, pas plus facile. Comme je l'ai déjà dit, chaque équation accroche les ressorts, dans ce cas, le ressort entre x0 et la valeur 1, le ressort entre x18 et la valeur 2, et enfin, la variable x31 sera également attirée vers l'unité.

Mais le coefficient de 100 est là pour une raison. Nous nous souvenons que ce système ne peut tout simplement pas être résolu, nous le résolvons dans le sens des moindres carrés, en minimisant la fonction quadratique correspondante. En multipliant par 100 chacun des coefficients des trois dernières équations, nous introduisons une pénalité pour l'écart de x0, x18 et x32 par rapport aux valeurs souhaitées, dix mille fois (100 ^ 2) dépassant la pénalité pour écart de l'égalité$$$x_i = x_{i+1}$ .En gros, les ressorts sur les trois dernières équations sont dix mille fois plus durs que sur toutes les autres. Cette méthode de pénalité quadratique est un outil très pratique pour introduire des restrictions; elle est beaucoup plus simple (mais pas sans inconvénients) que de réduire un ensemble de variables.

Exemple deux, en trois dimensions

Passons à quelque chose de plus intéressant que de lisser les éléments d'un tableau unidimensionnel! Pour commencer, nous ferons exactement la même chose, mais avec des données plus intéressantes et avec de vrais outils. Je veux prendre une surface en trois dimensions, fixer sa bordure et lisser le reste de la surface autant que possible:



Le code est disponible ici , mais juste au cas où je donnerais une liste complète du fichier principal:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

J'ai écrit l'analyseur le plus simple des fichiers .obj de front d'onde, donc le modèle est chargé sur une seule ligne. En tant que solveur, j'utiliserai OpenNL, c'est un solveur très puissant pour les problèmes de moindres carrés avec des matrices clairsemées. Veuillez noter que les dimensions des matrices peuvent être gigantesques: par exemple, si nous voulons obtenir une image en noir et blanc avec une taille de 1000 x 1000 pixels, alors la matrice$$$A^\top A$nous aurons une taille d'un million par million! Cependant, dans la pratique, le plus souvent, la grande majorité des éléments de cette matrice sont nuls, donc tout n'est pas si effrayant, mais vous devez toujours utiliser des solveurs spéciaux.

Examinons donc le code. Pour commencer, j'annonce au solveur ce que je veux faire:

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

Je veux avoir une matrice $$$A^\top A$taille (nombre de sommets) x (nombre de sommets). Attention, nous donnons au solveur une matrice$$$A$ et $$$A^\top A$il le construira lui-même, ce qui est très pratique! Faites également attention au fait que je ne résout pas un système d'équations, mais trois en série pour x, y et z (j'ai menti que le problème est tridimensionnel, il est toujours unidimensionnel!)

Et puis je déclare ligne par ligne de notre matrice. Pour commencer, je fixe les sommets qui sont sur le bord de la surface:

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

Vous pouvez voir que j'utilise une pénalité carrée de 100 ^ 2 pour fixer les sommets des bords.

Eh bien, pour chaque paire de sommets adjacents, j'accroche un ressort de rigidité 1 entre eux:

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

Nous exécutons le code et voyons comment le visage s'est lissé dans la surface du film de savon sur un fil incurvé. Nous venons de résoudre le problème de Dirichlet, ayant obtenu une surface de surface minimale.

Nous améliorons les caractéristiques

Transformons notre visage en un masque grotesque:



dans l'article précédent, j'ai déjà montré comment le faire sur le genou, je donne ici un vrai code qui utilise le solveur des moindres carrés:

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

Le code complet est disponible ici . Comment fonctionne-t-il? Comme dans l'exemple précédent, je commence par fixer les sommets des bords. Ensuite, pour chaque bord, je dis (tranquillement, avec un coefficient de 0,2) que ce serait bien s'il avait exactement la même forme que dans la surface d'origine:

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

Si vous ne faites rien de plus et résolvez le problème tel qu'il est, alors nous devrions obtenir exactement ce qui était à la sortie à la sortie: la bordure de sortie est égale à la bordure d'entrée, plus les différences de sortie sont égales aux différences d'entrée.

Mais nous ne nous arrêterons pas là!

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

J'ajoute plus d'équations à notre système. Pour chaque sommet, je compte la courbure de la surface autour d'elle dans la surface d'entrée, et je la multiplie par deux et demi, c'est-à-dire que la surface de sortie doit avoir une grande courbure partout.

Ensuite, nous appelons notre solveur et obtenons une bonne caricature.

Dernier exemple pour aujourd'hui

Jusqu'à ce moment, nous n'avons pas vu un seul nouvel exemple, tout était déjà montré dans l'article précédent. Essayons de faire quelque chose de moins trivial que le lissage le plus simple, qui peut être facilement obtenu sans utiliser de solveurs. Le code est disponible ici , mais permettez-moi de vous donner une liste:

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

Nous travaillons toujours sur la même surface qu'auparavant; nous appelons la fonction snap () pour chaque triangle. Cette fonction indique quel axe du système de coordonnées est le plus proche de la normale de ce triangle. Autrement dit, nous voulons savoir que ce triangle est plus probablement vertical ou horizontal. Eh bien, alors nous voulons changer la géométrie de notre surface afin que ce qui est proche de l'horizontale se rapproche encore plus! La partie gauche de cette image montre le résultat de la fonction snap ():



Ainsi, nous avons peint notre surface en trois couleurs, correspondant aux trois axes du système de coordonnées. Eh bien, pour chaque bord de notre système, nous ajoutons les équations suivantes:

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

Autrement dit, nous demandons à chaque bord de la surface de sortie de ressembler au bord correspondant de la surface d'entrée, à la rigidité du ressort 1. Et puis, si nous autorisons, par exemple, la dimension x, et que le bord doit être vertical, nous disons simplement qu'un sommet est égal à l'autre avec la rigidité du ressort 2:

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

Eh bien, voici le résultat de notre programme: Une



question parfaitement raisonnable: les idoles de l'île de Pâques, c'est bien sûr cool, mais qu'est-ce que la géologie a à voir avec ça? Y a-t-il des exemples de problèmes réels?

Oui bien sûr.Prenons une section de la croûte terrestre:



pour les géologues, les couches de roches différentes sont très importantes, les limites (horizons) entre lesquelles sont indiquées en vert et les failles géologiques qui sont indiquées en rouge. Nous avons en entrée une grille de triangles (tétraèdres en 3D) de la zone qui nous intéresse, mais des quads (hexaèdres en 3D) sont nécessaires pour modéliser certains processus. Nous déformons notre modèle pour que les failles deviennent verticales et les horizons (surprise) horizontaux:



Ensuite, nous prenons simplement une grille régulière de carrés, coupons notre domaine en carrés uniformes, et leur appliquons la transformation inverse, obtenant la grille de quads nécessaire.

Conclusion

Les méthodes des moindres carrés sont un puissant outil de traitement des données, et elles sont utilisées beaucoup plus largement que les statistiques dans les colonnes Excel. Ces possibilités s'offrent à nous du fait que minimiser une fonction quadratique et résoudre un système d'équations linéaires sont une seule et même chose, et nous (l'humanité) avons appris à résoudre des équations linéaires très, très bien, voire complètement de tailles inhumaines avec des milliards de variables.

Cependant, il arrive que nous n'ayons pas assez de modèles linéaires. Et ici, par exemple, les réseaux de neurones peuvent venir à la rescousse. Dans le prochain article, je vais essayer de montrer que l'OLS avec rejet des émissions est équivalent à l'une des formulations des réseaux de neurones. Restez en ligne!