RayTracing compréhensible en 256 lignes de C ++ nu
Ceci est un autre chapitre de mon bref cours de conférences sur l'infographie . Cette fois, nous parlons du lancer de rayons. Comme d'habitude, j'essaie d'éviter les bibliothèques tierces, car je pense que cela permet aux étudiants de vérifier ce qui se passe sous le capot. Vérifiez également le projet tinykaboom .
Il existe de nombreux articles sur le lancer de rayons sur le Web; cependant, le problème est que presque tous présentent des logiciels finis qui peuvent être assez difficiles à comprendre. Prenons, par exemple, le très célèbre défi du traceur de rayons de cartes d'affaires . Il produit des programmes très impressionnants, mais il est très difficile de comprendre comment cela fonctionne. Plutôt que de montrer que je peux faire des rendus, je veux vous expliquer en détail comment vous pouvez le faire vous-même.
Remarque: Cela n'a aucun sens de regarder mon code, ni de lire cet article avec une tasse de thé à la main. Cet article est conçu pour que vous puissiez utiliser le clavier et implémenter votre propre moteur de rendu. Ce sera sûrement mieux que le mien. Changez à tout le moins le langage de programmation!
Donc, l'objectif d'aujourd'hui est d'apprendre à rendre de telles images:

Étape 1: écrire une image sur le disque
Je ne veux pas m'embêter avec les gestionnaires de fenêtres, le traitement souris / clavier et des trucs comme ça. Le résultat de notre programme sera une simple image enregistrée sur le disque. Donc, la première chose que nous devons pouvoir faire est de sauvegarder l'image sur le disque. Ici vous pouvez trouver le code qui nous permet de le faire. Permettez-moi de lister le fichier principal:
#include <limits> #include <cmath> #include <iostream> #include <fstream> #include <vector> #include "geometry.h" void render() { const int width = 1024; const int height = 768; std::vector<Vec3f> framebuffer(width*height); for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } } std::ofstream ofs; // save the framebuffer to file ofs.open("./out.ppm"); ofs << "P6\n" << width << " " << height << "\n255\n"; for (size_t i = 0; i < height*width; ++i) { for (size_t j = 0; j<3; j++) { ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j]))); } } ofs.close(); } int main() { render(); return 0; }
Seul render () est appelé dans la fonction principale et rien d'autre. Que contient la fonction render ()? Tout d'abord, je définis le framebuffer comme un tableau unidimensionnel de valeurs Vec3f, ce sont de simples vecteurs tridimensionnels qui nous donnent des valeurs (r, g, b) pour chaque pixel. La classe des vecteurs vit dans le fichier geometry.h, je ne la décrirai pas ici: c'est vraiment une manipulation triviale de vecteurs bidimensionnels et tridimensionnels (addition, soustraction, affectation, multiplication par un scalaire, produit scalaire).
J'enregistre l'image au format ppm . C'est le moyen le plus simple d'enregistrer des images, mais ce n'est pas toujours le moyen le plus pratique de les visualiser davantage. Si vous souhaitez enregistrer dans d'autres formats, je vous recommande de lier une bibliothèque tierce, telle que stb . C'est une excellente bibliothèque: il vous suffit d'inclure un fichier d'en-tête stb_image_write.h dans le projet, et cela vous permettra d'enregistrer des images dans les formats les plus courants.
Attention: mon code est plein de bugs, je les corrige en amont, mais les commits plus anciens sont affectés. Vérifiez ce problème .
Donc, le but de cette étape est de s'assurer que nous pouvons a) créer une image en mémoire + affecter différentes couleurs et b) enregistrer le résultat sur le disque. Ensuite, vous pouvez le visualiser dans un logiciel tiers. Voici le résultat:

Étape 2, cruciale: le lancer de rayons
Il s'agit de l'étape la plus importante et la plus difficile de toute la chaîne. Je veux définir une sphère dans mon code et la dessiner sans être obsédé par les matériaux ou l'éclairage. Voici à quoi devrait ressembler notre résultat:

Par souci de commodité, j'ai un commit par étape dans mon référentiel; Github permet de visualiser très facilement les modifications apportées. Ici, par exemple , ce qui a été changé par le deuxième commit.
Pour commencer, de quoi avons-nous besoin pour représenter la sphère dans la mémoire de l'ordinateur? Quatre nombres suffisent: un vecteur tridimensionnel pour le centre de la sphère et un scalaire décrivant le rayon:
struct Sphere { Vec3f center; float radius; Sphere(const Vec3f &c, const float &r) : center(c), radius(r) {} bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const { Vec3f L = center - orig; float tca = L*dir; float d2 = L*L - tca*tca; if (d2 > radius*radius) return false; float thc = sqrtf(radius*radius - d2); t0 = tca - thc; float t1 = tca + thc; if (t0 < 0) t0 = t1; if (t0 < 0) return false; return true; } };
La seule chose non triviale dans ce code est une fonction qui vous permet de vérifier si un rayon donné (originaire de l'origine dans la direction de dir) croise notre sphère. Une description détaillée de l'algorithme pour l'intersection rayon-sphère peut être trouvée ici , je vous recommande fortement de le faire et de vérifier mon code.
Comment fonctionne le lancer de rayons? C'est assez simple. À la première étape, nous venons de remplir l'image avec un dégradé de couleurs:
for (size_t j = 0; j<height; j++) { for (size_t i = 0; i<width; i++) { framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0); } }
Maintenant, pour chaque pixel, nous formerons un rayon provenant de l'origine et traversant notre pixel, puis vérifier si ce rayon intersecte avec la sphère:

S'il n'y a pas d'intersection avec la sphère, nous dessinons le pixel avec color1, sinon avec color2:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { float sphere_dist = std::numeric_limits<float>::max(); if (!sphere.ray_intersect(orig, dir, sphere_dist)) { return Vec3f(0.2, 0.7, 0.8);
À ce stade, je vous recommande de prendre un crayon et de vérifier sur papier tous les calculs (l'intersection rayon-sphère et le balayage de l'image avec les rayons). Au cas où, notre caméra est déterminée par les éléments suivants:
- largeur de l'image
- hauteur de l'image
- angle de champ de vision
- emplacement de la caméra, Vec3f (0.0.0)
- voir la direction, le long de l'axe z, dans le sens de moins l'infini
Permettez-moi d'illustrer comment nous calculons la direction initiale du rayon à tracer. Dans la boucle principale, nous avons cette formule:
float x = (2*(i + 0.5)/(float)width - 1)*tan(fov/2.)*width/(float)height; float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);
D'où ça vient? Assez simple. Notre caméra est placée à l'origine et fait face à la direction -z. Permettez-moi d'illustrer les choses, cette image montre la caméra depuis le haut, l'axe y pointe hors de l'écran:
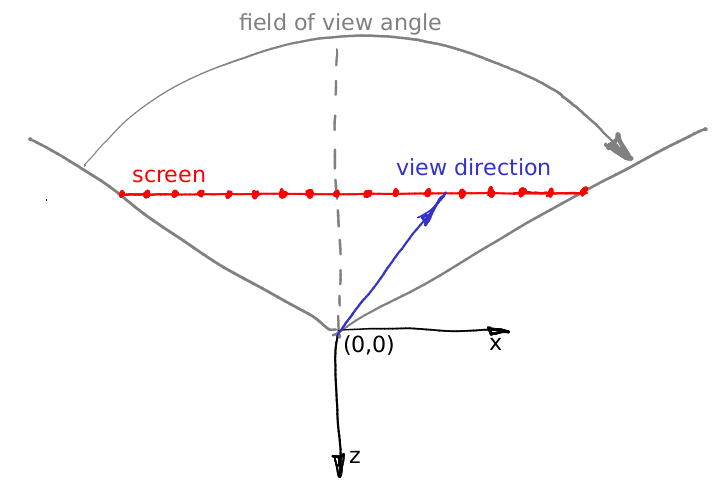
Comme je l'ai dit, la caméra est placée à l'origine, et la scène est projetée sur l'écran qui se trouve dans le plan z = -1. Le champ de vision spécifie quel secteur de l'espace sera visible à l'écran. Dans notre image, l'écran fait 16 pixels de large; pouvez-vous calculer sa longueur en coordonnées mondiales? C'est assez simple: concentrons-nous sur le triangle formé par la ligne pointillée rouge, grise et grise. Il est facile de voir que le bronzage (champ de vision / 2) = (largeur d'écran) 0,5 / (distance écran-caméra). Nous avons placé l'écran à une distance de 1 de la caméra, donc (largeur d'écran) = 2 bronzage (champ de vision / 2).
Disons maintenant que nous voulons projeter un vecteur à travers le centre du 12ème pixel de l'écran, c'est-à-dire que nous voulons calculer le vecteur bleu. Comment faire ça? Quelle est la distance entre la gauche de l'écran et la pointe du vecteur bleu? Tout d'abord, c'est 12 + 0,5 pixels. Nous savons que 16 pixels de l'écran correspondent à 2 unités mondiales tan (fov / 2). Ainsi, la pointe du vecteur est située à (12 + 0,5) / 16 2 tan (fov / 2) unités mondiales du bord gauche, ou à la distance de (12 + 0,5) 2/16 * tan (fov / 2) - bronzage (fov / 2) à partir de l'intersection entre l'écran et l'axe -z. Ajoutez le rapport hauteur / largeur de l'écran aux calculs et vous trouverez exactement les formules pour la direction des rayons.
Étape 3: ajouter plus de sphères
La partie la plus difficile est terminée, et maintenant notre chemin est clair. Si nous savons dessiner une sphère, il ne nous faudra pas longtemps pour en ajouter quelques autres. Vérifiez les modifications dans le code, et voici l'image résultante:

Étape 4: éclairage
L'image est parfaite sous tous les aspects, à l'exception du manque de lumière. Dans le reste de l'article, nous parlerons de l'éclairage. Ajoutons quelques sources lumineuses ponctuelles:
struct Light { Light(const Vec3f &p, const float &i) : position(p), intensity(i) {} Vec3f position; float intensity; };
Le calcul de l'illumination globale réelle est une tâche très, très difficile, donc comme tout le monde, nous tromperons l'œil en dessinant des résultats complètement non physiques, mais visuellement plausibles. Pour commencer: pourquoi fait-il froid en hiver et chaud en été? Parce que le chauffage de la surface de la Terre dépend de l'angle d'incidence des rayons du soleil. Plus le soleil s'élève au-dessus de l'horizon, plus la surface est lumineuse. Inversement, plus il est bas au-dessus de l'horizon, plus il est sombre. Et après le coucher du soleil sur l'horizon, les photons ne nous atteignent même pas du tout.
Retour nos sphères: nous émettons un rayon de la caméra (pas de relation avec les photons!) À elle s'arrête à une sphère. Comment savons-nous l'intensité de l'éclairage du point d'intersection? En effet, il suffit de vérifier l'angle entre un vecteur normal en ce point et le vecteur décrivant une direction de la lumière. Plus l'angle est petit, meilleure est la surface éclairée. Rappelons que le produit scalaire entre deux vecteurs a et b est égal au produit des normes des vecteurs multiplié par le cosinus de l'angle entre les vecteurs: a * b = | a | | b | cos (alpha (a, b)). Si nous prenons des vecteurs de longueur unitaire, le produit scalaire nous donnera l'intensité de l'éclairage de surface.
Ainsi, dans la fonction cast_ray, au lieu d'une couleur constante, nous retournerons la couleur en tenant compte des sources lumineuses:
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) { [...] float diffuse_light_intensity = 0; for (size_t i=0; i<lights.size(); i++) { Vec3f light_dir = (lights[i].position - point).normalize(); diffuse_light_intensity += lights[i].intensity * std::max(0.f, light_dir*N); } return material.diffuse_color * diffuse_light_intensity; }
Les modifications par rapport à l'étape précédente sont disponibles ici , et voici le résultat:

Étape 5: éclairage spéculaire
L'astuce du produit scalaire donne une bonne approximation de l'éclairage des surfaces mates, dans la littérature, il est appelé éclairage diffus. Que devons-nous faire si nous voulons dessiner des surfaces brillantes? Je veux obtenir une photo comme celle-ci:

Vérifiez combien de modifications ont été nécessaires. En bref, plus la lumière est brillante sur les surfaces brillantes, moins l'angle entre la direction de la vue et la direction de la lumière réfléchie est faible.
Cette supercherie avec illumination de surfaces mates et brillantes est connue sous le nom de modèle de réflexion Phong . Le wiki a une description assez détaillée de ce modèle d'éclairage. Il peut être agréable de le lire côte à côte avec le code source. Voici l'image clé pour comprendre la magie:

Étape 6: ombres
Pourquoi avons-nous la lumière, mais pas d'ombres? Ce n'est pas bien! Je veux cette photo:

Seules six lignes de code nous permettent d'atteindre cet objectif: lors du dessin de chaque point, nous nous assurons simplement que le segment entre le point actuel et la source de lumière n'intersecte pas les objets de notre scène. S'il y a une intersection, nous sautons la source de lumière actuelle. Il n'y a qu'une petite subtilité: je perturbe le point en le déplaçant dans le sens normal:
Vec3f shadow_orig = light_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Pourquoi ça? C'est juste que notre point se trouve sur la surface de l'objet, et (à l'exception de la question des erreurs numériques) tout rayon de ce point coupera l'objet lui-même.
Étape 7: réflexions
C'est incroyable, mais pour ajouter des reflets à notre rendu, il suffit d'ajouter trois lignes de code:
Vec3f reflect_dir = reflect(dir, N).normalize(); Vec3f reflect_orig = reflect_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;
Voyez par vous-même: lorsque vous intersectez la sphère, nous calculons simplement le rayon réfléchi (à l'aide de la même fonction que nous avons utilisée pour les reflets spéculaires!) Et appelons récursivement la fonction cast_ray dans la direction du rayon réfléchi. Assurez-vous de jouer avec la profondeur de récursivité , je la mets à 4, essayez différentes valeurs commençant à 0, qu'est-ce qui va changer dans l'image? Voici mon résultat avec des réflexions et une profondeur de récursivité de 4:

Étape 8: réfractions
Si nous savons faire des réflexions, les réfractions sont faciles . Nous devons ajouter une fonction pour calculer le rayon réfracté (en utilisant la loi de Snell ), et trois autres lignes de code dans notre fonction récursive cast_ray. Voici le résultat où la boule la plus proche est "en verre", elle réfléchit et réfracte la lumière en même temps:

Steo 9: au-delà des sphères
Jusqu'à présent, nous n'avons rendu que des sphères car il s'agit de l'un des objets mathématiques les plus simples non triviaux. Ajoutons un avion. L'échiquier est un choix classique. Pour cela, il suffit de rajouter une dizaine de lignes .
Et voici le résultat:

Comme promis, le code a 256 lignes de code, vérifiez par vous-même !
Étape 10: affectation à domicile
Nous avons parcouru un long chemin: nous avons appris comment ajouter des objets à une scène, comment calculer un éclairage plutôt compliqué. Permettez-moi de vous laisser deux devoirs comme devoirs. Absolument tout le travail préparatoire a déjà été fait dans la branche homework_assignment . Chaque affectation nécessitera dix lignes de sommets de code.
Affectation 1: carte de l'environnement
Pour le moment, si le rayon ne coupe aucun objet, nous définissons simplement le pixel sur la couleur d'arrière-plan constante. Et pourquoi, en fait, est-ce constant? Prenons une photo sphérique (fichier envmap.jpg ) et utilisons-la comme arrière-plan! Pour vous faciliter la vie, j'ai lié notre projet à la bibliothèque stb pour la commodité de travailler avec le format jpg. Cela devrait nous donner une telle image:

Devoir 2: charlatan-charlatan!
Nous pouvons rendre des sphères et des plans (voir le damier). Alors dessinons des mailles triangulaires! J'ai écrit un code qui vous permet de lire un fichier .obj et y ai ajouté une fonction d'intersection rayon-triangle. Maintenant, ajouter le canard à notre scène devrait être assez banal:

Conclusion
Mon objectif principal est de montrer des projets intéressants (et faciles!) À programmer. Je suis convaincu que pour devenir un bon programmeur, il faut faire beaucoup de projets parallèles. Je ne sais pas pour vous, mais personnellement je ne suis pas attiré par les logiciels de comptabilité et le jeu de dragueur de mines, même si la complexité du code est assez comparable.
Quelques heures et deux cent cinquante lignes de code nous donnent un raytracer. Cinq cents lignes du rasterizer logiciel peuvent être réalisées en quelques jours. Le graphisme est vraiment cool pour apprendre la programmation!