Clone Numpy

Un petit module pour travailler avec des tableaux en Python sans utiliser de bibliothèques tierces (un clone NumPy, mais uniquement en Python pur).

Les devoirs à l'université ont été invités à écrire un programme qui calcule les normes et les décompositions de la matrice, mais il a été interdit d'utiliser des bibliothèques tierces. Le choix du langage de programmation n'est pas limité. J'ai choisi python (ce qui était une erreur, car il est beaucoup plus lent que Java et C / C ++) et je ne peux donc pas utiliser NumPy. Dans le processus, j'ai dû écrire des fonctions pour effectuer des opérations avec des tableaux, des fonctions pour trouver des mineurs, des déterminants, etc. Le résultat est une mini bibliothèque pour travailler avec des tableaux.

Mon code python pur est beaucoup plus lent que NumPy, qui effectue les calculs C et Fortran (en plus mon code n'est pas optimisé).

Que peut MatLOL:

• Somme, différence et produit des matrices
• Produit matriciel par numéro
• Transposition matricielle
• Matrice mineure
• Déterminant de la matrice
• Matrice inverse
• Matrice d'union
• Numéro de condition de la matrice
• Normes matricielles première, deuxième (non finalisées), euclidienne et infinie
• Solution de l'équation AX = B
• Décomposition LU
• Décomposition Cholesky
• Méthode Seidel

Exemples MathLOL

Importez le module:

# from mathlol import * from mathlol import mathlol 

Initialisation de la matrice

 matrix = mathlol() matrix.set([[1, 2, 3], [4, 5, 6], [7, -8, 9]]) matrix.get() #   

Quelques opérations matricielles

 matrix * 2 #     2 A = [[0, 0, 0], [0, 1, 0], [0, 0, 0]] #  2  matrix.dot(A) matrix * A matrix.transposition() #   matrix.minor(i = 0, j = 0) #   matrix.determinant() #   matrix.inverse() #   L, U = matrix.lu() # LU  matrix.seidel(b = [[5.0], [9.0], [1.0]]) #   

Il existe également des fonctions pour travailler avec des vecteurs

 vector = mathlol() vector.set([1, 2, 3, 4, 5]) vector.checkvector() # ,     vector.norm1_vector() vector.norm2_vector() vector.norm3_vector() 

Autres exemples

Performance MathLOL

Voyons la vitesse de calcul des produits de matrices de taille NxN. Les matrices sont remplies d'entiers aléatoires de -100 à 100.




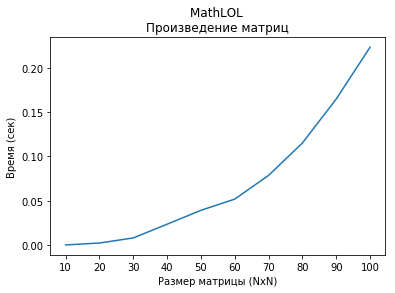
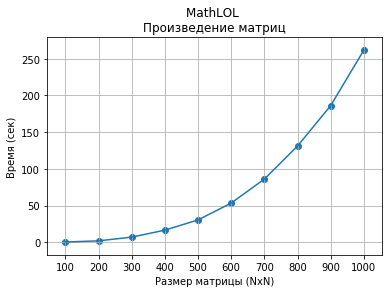
La vitesse de calcul des tailles de produits matriciels de 100x100 à 1000x1000



Comparez la vitesse de calcul de numpy et mathlol. Malheureusement, le mathlol était très lent et j'ai décidé de prendre des matrices pour des tailles de 100x100 à 1000x1000 pour numpy, et de 10x10 à 100x100 pour mathlol.



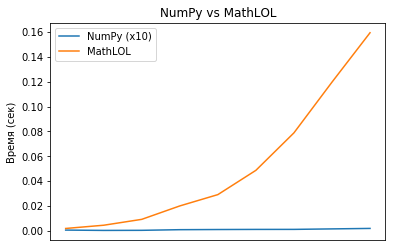
MathLOL a calculé le produit de la matrice 100x100 par lui-même en 0,16 seconde, et NumPy a calculé le produit de la matrice 1000x1000 par lui-même en 0,002 (!!!) secondes. La différence est énorme.

Notre tâche consistait simplement à implémenter diverses fonctions pour travailler avec des matrices, ce que nous avons fait, mais le programme avec de grandes matrices ne fonctionne pas aussi rapidement que nous le souhaiterions. Il reste à affiner le programme, à ajouter quelques fonctions supplémentaires (par exemple, une fonction pour calculer le nombre de Todd), je vous serais reconnaissant de bien vouloir regarder le code, signaler les erreurs et peut-être aider à affiner le code.

C'est tout, le code et les exemples sont affichés sur le github .

PS En train d'écrire l'article, j'ai voulu expérimenter et intégrer C / C ++ dans mon module. Je vais m'en occuper dans un proche avenir et voir à quel point ce sera proche des performances de NumPy.