
En octobre, le deuxième championnat de programmation a eu lieu. Nous avons reçu 12 500 candidatures, plus de 6 000 personnes se sont essayées aux compétitions. Cette fois, les participants ont pu choisir l'une des pistes suivantes: backend, frontend, développement mobile et apprentissage automatique. Dans chaque piste, il fallait passer l'étape de qualification et la finale.
Par tradition, nous publierons des analyses de pistes sur Habré. Commençons par les tâches de la phase de qualification du machine learning. L'équipe a préparé cinq de ces tâches, parmi lesquelles il y avait deux options pour trois tâches: dans la première version, il y avait les tâches A1, B1 et C, dans la seconde - A2, B2 et C. Les options étaient réparties au hasard entre les participants. L'auteur de la tâche C est notre développeur Pavel Parkhomenko, le reste des tâches a été réalisé par son collègue Nikita Senderovich.
Pour la première tâche algorithmique simple (A1 / A2), les participants pouvaient obtenir 50 points en énumérant correctement la réponse. Pour la deuxième tâche (B1 / B2), nous avons donné de 10 à 100 points - selon l'efficacité de la solution. Pour obtenir 100 points, il fallait implémenter la méthode de programmation dynamique. La troisième tâche a été consacrée à la construction d'un modèle de clic basé sur les données de formation fournies. Il fallait appliquer des méthodes de travail avec des attributs catégoriels et utiliser un modèle non linéaire de formation (par exemple, le renforcement du gradient). Pour la tâche, il était possible d'obtenir jusqu'à 150 points - selon la valeur de la fonction de perte sur l'échantillon d'essai.
A1. Restaurer la longueur du carrousel
Condition
Le système de recommandation devrait déterminer efficacement les intérêts des personnes. Et en plus des méthodes d'apprentissage automatique, des solutions d'interface spéciales sont utilisées pour effectuer cette tâche, qui demandent explicitement à l'utilisateur ce qui l'intéresse. Une telle solution est le carrousel.
Un carrousel est un ruban horizontal de cartes, chacune proposant de s'abonner à une source ou un sujet spécifique. La même carte se retrouve plusieurs fois dans le carrousel. Le carrousel peut défiler de gauche à droite, tandis qu'après la dernière carte, l'utilisateur voit à nouveau la première. Pour l'utilisateur, le passage de la dernière carte à la première est invisible, de son point de vue la bande est interminable.
À un moment donné, un utilisateur curieux, Vasily, a remarqué que la bande était en boucle et a décidé de découvrir la vraie longueur du carrousel. Pour ce faire, il a commencé à faire défiler la bande et à écrire séquentiellement les cartes de réunion, pour plus de simplicité, en désignant chaque carte par une lettre latine minuscule. Vasily a donc écrit les n premières cartes sur un morceau de papier. Il est garanti qu'il a regardé toutes les cartes du carrousel au moins une fois. Puis Vasily s'est couché, et le matin il a découvert que quelqu'un avait renversé un verre d'eau sur ses notes et maintenant certaines lettres ne pouvaient pas être reconnues.
Selon les informations restantes, aidez Vasily à déterminer le plus petit nombre possible de cartes dans le carrousel.
Formats d'E / S et exemplesFormat d'entrée
La première ligne contient un seul entier n (1 ≤ n ≤ 1000) - le nombre de caractères écrits par Vasily.
La deuxième ligne contient la séquence écrite par Vasily. Il se compose de n caractères - lettres latines minuscules et signe #, ce qui signifie que la lettre à cette position ne peut pas être reconnue.
Format de sortie
Imprimez un seul nombre entier positif - le plus petit nombre possible de cartes dans le carrousel.
Exemple 1
Exemple 2
Exemple 3
Exemple 4
Remarques
Dans le premier exemple, toutes les lettres ont été reconnues, le carrousel minimum pourrait être composé de 3 cartes - abc.
Dans le deuxième exemple, toutes les lettres ont été reconnues, le carrousel minimum pourrait être composé de 3 cartes - abb. Veuillez noter que les deuxième et troisième cartes de ce carrousel sont identiques.
Dans le troisième exemple, la longueur de carrousel la plus petite possible est obtenue si nous supposons que le symbole a était en troisième position. Ensuite, la ligne initiale est ababa, le carrousel minimum se compose de 2 cartes - ab.
Dans le quatrième exemple, la chaîne source peut être n'importe quoi, par exemple ffffff. Le carrousel pourrait alors consister en une seule carte - f.
Système de notation
Ce n'est qu'après avoir réussi tous les tests de la tâche que vous pouvez obtenir
50 points .
Dans le système de test, les tests 1 à 4 sont des exemples de la condition.
Solution
Il suffisait de trier la longueur possible du carrousel de 1 à n et pour chaque longueur fixe de vérifier s'il pouvait l'être. Il est clair que la réponse existe toujours, car la valeur de n est garantie d'être une réponse possible. Pour une longueur de carrousel fixe p, il suffit de vérifier que dans la chaîne transmise pour tout i de 0 à (p - 1) à toutes les positions i, i + p, i + 2p, etc., les mêmes caractères ou # sont trouvés. Si au moins pour certains i, il y a 2 caractères différents dans la plage de a à z, alors le carrousel ne peut pas être de longueur p. Puisque dans le pire des cas, pour chaque p, vous devez parcourir tous les caractères de la chaîne une fois, la complexité de cet algorithme est O (n
2 ).
def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break
A2. Restaurer la longueur du carrousel
Condition
Le système de recommandation devrait déterminer efficacement les intérêts des personnes. Et en plus des méthodes d'apprentissage automatique, des solutions d'interface spéciales sont utilisées pour effectuer cette tâche, qui demandent explicitement à l'utilisateur ce qui l'intéresse. Une telle solution est le carrousel.
Un carrousel est un ruban horizontal de cartes, chacune proposant de s'abonner à une source ou un sujet spécifique. La même carte se retrouve plusieurs fois dans le carrousel. Le carrousel peut défiler de gauche à droite, tandis qu'après la dernière carte, l'utilisateur voit à nouveau la première. Pour l'utilisateur, le passage de la dernière carte à la première est invisible, de son point de vue la bande est interminable.
À un moment donné, un utilisateur curieux, Vasily, a remarqué que la bande était en boucle et a décidé de découvrir la vraie longueur du carrousel. Pour ce faire, il a commencé à faire défiler la bande et à écrire séquentiellement les cartes de réunion, pour plus de simplicité, en désignant chaque carte par une lettre latine minuscule. Vasily a donc écrit les n premières cartes. Il est garanti qu'il a regardé toutes les cartes du carrousel au moins une fois. Étant donné que Vasily était distrait par le contenu des cartes, lors de l'écriture, il pouvait remplacer par erreur une lettre par une autre, mais on sait qu'au total, il n'a commis que k erreurs.
Les enregistrements réalisés par Vasily sont tombés entre vos mains, vous connaissez également la valeur de k. Déterminez le nombre de cartes dans son carrousel.
Formats d'E / S et exemplesFormat d'entrée
La première ligne contient deux nombres entiers: n (1 ≤ n ≤ 500) - le nombre de caractères écrits par Basil, et k (0 ≤ k ≤ n) - le nombre maximum d'erreurs que Vasily a faites.
La deuxième ligne contient n lettres minuscules de l'alphabet latin - la séquence écrite par Vasily.
Format de sortie
Imprimez un seul nombre entier positif - le plus petit nombre possible de cartes dans le carrousel.
Exemple 1
Exemple 2
Exemple 3
Exemple 4
Remarques
Dans le premier exemple, k = 0, et nous savons avec certitude que Vasily ne s'est pas trompé, le carrousel minimum pourrait être composé de 3 cartes - abc.
Dans le deuxième exemple, la longueur de carrousel la plus petite possible est obtenue si nous supposons que Vasily a remplacé par erreur la troisième lettre a par c. Ensuite, la vraie ligne est ababa, le carrousel minimum se compose de 2 cartes - ab.
Dans le troisième exemple, on sait que Vasily pourrait faire une erreur. Cependant, la taille du carrousel est minime, en supposant qu'il n'a pas commis d'erreur. Le carrousel minimum se compose de 3 cartes - abb. Veuillez noter que les deuxième et troisième cartes de ce carrousel sont identiques.
Dans le quatrième exemple, nous pouvons dire que Vasily s'est trompé en entrant toutes les lettres, et la ligne d'origine pourrait en fait être n'importe laquelle, par exemple ffffff. Le carrousel pourrait alors consister en une seule carte - f.
Système de notation
Ce n'est qu'après avoir réussi tous les tests de la tâche que vous pouvez obtenir
50 points .
Dans le système de test, les tests 1 à 4 sont des exemples de la condition.
Solution
Il suffisait de trier la longueur possible du carrousel de 1 à n et pour chaque longueur fixe de vérifier s'il pouvait l'être. Il est clair que la réponse existe toujours, puisque la valeur de n est garantie d'être une réponse possible, quelle que soit la valeur de k. Pour une longueur de carrousel fixe p, il suffit de calculer indépendamment pour tout i de 0 à (p - 1) le nombre minimum d'erreurs aux positions i, i + p, i + 2p, etc. Ce nombre d'erreurs est minime s'il est considéré comme vrai le symbole est celui que l'on retrouve le plus souvent dans ces positions. Ensuite, le nombre d'erreurs est égal au nombre de positions sur lesquelles se trouve une autre lettre. Si pour certains p le nombre total d'erreurs ne dépasse pas k, alors la valeur p est une réponse possible. Puisque pour chaque p vous devez parcourir tous les caractères de la chaîne une fois, la complexité de cet algorithme est O (n
2 ).
n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break
B1. Ruban de recommandation optimal
Condition
La formation de la partie suivante de l'émission personnelle de recommandations pour l'utilisateur n'est pas une tâche facile. Considérez n publications sélectionnées à partir d'une base de recommandations basée sur la sélection des candidats. Le numéro de publication i est caractérisé par un score de pertinence s
i et un ensemble de k attributs binaires a
i1 , a
i2 , ..., a
ik . Chacun de ces attributs correspond à une propriété de la publication, par exemple, si l'utilisateur est abonné à la source de cette publication, si la publication a été créée au cours des dernières 24 heures, etc. La publication peut avoir plusieurs de ces propriétés à la fois, auquel cas les attributs correspondants prennent la valeur 1, ou il peut n'en avoir aucun - et alors tous ses attributs sont 0.
Pour que le flux de l'utilisateur soit diversifié, il est nécessaire de choisir parmi m candidats n publications pour qu'au moins il y ait A
1 publications ayant la première propriété, au moins A
2 publications ayant la deuxième propriété, ..., A
k publications ayant la propriété de numéro k. Trouvez le score de pertinence total maximum possible pour m publications qui satisfont à cette exigence, ou déterminez qu'un tel ensemble de publications n'existe pas.
Formats d'E / S et exemplesFormat d'entrée
La première ligne contient trois entiers - n, m, k (1 ≤ n ≤ 50, 1 ≤ m ≤ min (n, 9), 1 ≤ k ≤ 5).
Les n lignes suivantes montrent les caractéristiques des publications. Pour la i-ème publication, un entier s
i (1 ≤ s
i ≤ 10
9 ) est donné - une évaluation de la pertinence de cette publication, puis, après un espace, une chaîne de k caractères, dont chacun est 0 ou 1 - les valeurs de chacun des attributs de cette publication.
La dernière ligne contient k entiers séparés par des espaces - les valeurs A
1 , ..., A
k (0 ≤ A
i ≤ m) qui définissent les exigences pour l'ensemble final de m publications.
Format de sortie
S'il n'y a pas un ensemble de m publications satisfaisant aux restrictions, imprimez le numéro 0. Sinon, imprimez un seul nombre entier positif - le score de pertinence totale maximum possible.
Exemple 1
Exemple 2
Remarques
Dans le premier exemple, parmi quatre publications avec deux propriétés, deux doivent être sélectionnées de sorte qu'il y ait au moins une publication qui a la première propriété et une qui a la deuxième propriété. La plus grande pertinence peut être obtenue si nous prenons les deuxième et troisième publications, bien que toute option avec une quatrième publication soit également adaptée aux restrictions.
Dans le deuxième exemple, il est impossible de sélectionner deux publications afin que les deux possèdent la deuxième propriété, car seule la première publication en dispose.
Système de notation
Les tests pour cette tâche se composent de cinq groupes. Les points pour chaque groupe sont attribués uniquement lors de la réussite de tous les tests du groupe et de tous les tests des groupes
précédents . La réussite des tests des conditions est nécessaire pour obtenir des points pour les groupes à partir de la seconde. Au total pour la tâche, vous pouvez obtenir
100 points .
Dans le système de test, les tests 1-2 sont des exemples de la condition.
1.
(10 points) tests 3 à 10: k = 1, m ≤ 3, s
i ≤ 1000, aucun test n'est requis pour la condition
2.
(20 points) tests 11-20: k ≤ 2, m ≤ 3
3.
(20 points) tests 21-29: k ≤ 2
4.
(20 points) tests 30–37: k ≤ 3
5.
(30 points) tests 38–47: aucune restriction supplémentaire
Solution
Il y a n publications, chacune a une vitesse et k drapeaux booléens, il est nécessaire de sélectionner m cartes de telle sorte que la somme des pertinence soit maximale et k les exigences du formulaire «parmi les m publications sélectionnées doivent avoir ≥ A
i cartes avec le i-ème drapeau» soient remplies, ou déterminer que un tel ensemble de publications n'existe pas.
La décision est de 10 points : s'il y a exactement un drapeau, il suffit de prendre les publications A
1 avec ce drapeau qui sont les plus pertinentes (s'il y a moins de telles cartes que A
1 , alors le jeu souhaité n'existe pas), et le reste (m - A
1 ) doit être récupéré par les autres cartes avec la meilleure pertinence.
La solution est de 30 points : si m ne dépasse pas 3, alors vous pouvez trouver la réponse par une recherche exhaustive de tous les triplets de cartes O (n
3 ) possibles, choisissez la meilleure option en termes de pertinence totale qui satisfait aux restrictions.
La décision est de 70 points (50 points est le même, mais plus facile à mettre en œuvre): s'il n'y a pas plus de 3 drapeaux, vous pouvez diviser toutes les publications en 8 groupes disjoints selon l'ensemble de drapeaux qu'ils ont: 000, 001, 010, 011, 100, 101, 110, 111. Les publications de chaque groupe doivent être triées par ordre décroissant de pertinence. Ensuite, pour O (m
4 ), nous pouvons trier le nombre de meilleures publications que nous prenons des groupes 111, 011, 110 et 101. De chacune, nous prenons de 0 à m publications, au total pas plus de m. Après cela, il devient clair combien de publications doivent être collectées dans les groupes 100, 010 et 001 afin de satisfaire aux exigences. Il reste à se familiariser avec les cartes restantes avec la meilleure pertinence.
Solution complète : considérons la fonction de programmation dynamique dp [i] [a] ... [z]. Il s'agit du score de pertinence total maximum qui peut être obtenu en utilisant exactement i publications afin qu'il y ait exactement une publication avec le drapeau A, ..., z des publications avec le drapeau Z. Ensuite, initialement dp [0] [0] ... [0] = 0, et pour tous les autres ensembles de paramètres, nous définissons la valeur égale à -1 afin de maximiser cette valeur à l'avenir. Ensuite, nous allons «entrer dans le jeu» des cartes une à la fois et utiliser chaque carte pour améliorer les valeurs de cette fonction: pour chaque état de dynamique (i, a, b, ..., z) en utilisant la jième publication avec drapeaux (a
j , b
j , ..., z
j ), on peut essayer de faire une transition vers l'état (i + 1, a + a
j , b + b
j , ..., z + z
j ) et vérifier si le résultat s'améliore dans cet état. Important: pendant la transition, nous ne nous intéressons pas aux états où i ≥ m, par conséquent, les états totaux d'une telle dynamique ne dépassent pas m
k + 1 , et le comportement asymptotique résultant est O (nm
k + 1 ). Lorsque les états de dynamique sont calculés, la réponse est un état qui satisfait les contraintes et donne le score de pertinence total le plus élevé.
Du point de vue de l'implémentation, il est utile de stocker l'état de la programmation dynamique et les drapeaux de chaque publication sous forme packagée en un nombre entier pour accélérer le travail du programme (voir code), et non dans une liste ou un tuple. Cette solution utilise moins de mémoire et vous permet de mettre à jour efficacement l'état de la dynamique.
Code de solution complet:
def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score)
B2. Approximation des fonctions
Condition
Pour évaluer le degré de pertinence des documents, diverses méthodes d'apprentissage automatique sont utilisées - par exemple, des arbres de décision. L'arbre de décision k-aire a une règle de décision dans chaque nœud qui divise les objets en k classes en fonction des valeurs d'un attribut. En pratique, les arbres de décision binaires sont généralement utilisés. Considérons une version simplifiée du problème d'optimisation, qui doit être résolue dans chaque nœud de l'arbre de décision k-aire.
Soit une fonction discrète f définie aux points i = 1, 2, ..., n. Il est nécessaire de trouver une fonction constante par morceaux g composée de pas plus de k sections de constance telles que la valeur SSE =
s u m n i = 1 (g (i) - f (i))
2 est minime.
Formats d'E / S et exemplesFormat d'entrée
La première ligne contient deux entiers n et k (1 ≤ n ≤ 300, 1 ≤ k ≤ min (n, 10)).
La deuxième ligne contient n entiers f (1), f (2), ..., f (n) - les valeurs de la fonction approximative aux points 1, 2, ..., n (–10
6 ≤ f (i) ≤ 10
6 ).
Format de sortie
Imprimer un seul numéro - la valeur minimale possible de SSE. La réponse est considérée comme correcte si l'erreur absolue ou relative ne dépasse pas 10
–6 .
Exemple 1
Exemple 2
Exemple 3
Remarques
Dans le premier exemple, la fonction optimale g est la constante g (i) = 2.
SSE = (2 - 1)
2 + (2 - 2)
2 + (2 - 3)
2 = 2.
Dans le deuxième exemple, il y a 2 options. Soit g (1) = 1 et g (2) = g (3) = 2,5, soit g (1) = g (2) = 1,5 et
g (3) = 3. Dans tous les cas, SSE = 0,5.
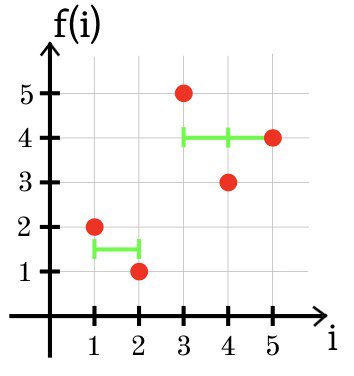
Dans le troisième exemple, l'approximation optimale de la fonction f en utilisant deux sections de constance est indiquée ci-dessous: g (1) = g (2) = 1,5 et g (3) = g (4) = g (5) = 4.
SSE = (1,5 + 2)
2 + (1,5 - 1)
2 + (4 - 5)
2 + (4 - 3)
2 + (4 - 4)
2 = 2,5.
Système de notation
Les tests pour cette tâche se composent de cinq groupes. Les points pour chaque groupe sont attribués uniquement lors de la réussite de tous les tests du groupe et de tous les tests des groupes
précédents . La réussite des tests des conditions est nécessaire pour obtenir des points pour les groupes à partir de la seconde. Au total pour la tâche, vous pouvez obtenir
100 points .
Dans le système de test, les tests 1-3 sont des exemples de la condition.
1.
(10 points) tests 4–22: k = 1, aucun test n'est requis pour la condition
2.
(20 points) tests 23-28: k ≤ 2
3.
(20 points) tests 29–34: k ≤ 3
4.
(20 points) tests 35–40: k ≤ 4
5.
(30 points) tests 41–46: aucune restriction supplémentaire
Solution
Comme vous le savez, la constante qui minimise la valeur SSE pour un ensemble de valeurs f
1 , f
2 , ..., f
n est la moyenne des valeurs répertoriées ici. De plus, comme il est facile de vérifier par de simples calculs, la valeur SSE =
s u m s q u a r e v a l u e s - f r a c de la q u a r e s u m v a l u e s n .
La décision est de 10 points : nous considérons simplement la moyenne de toutes les valeurs de la fonction et de l'ESS comme O (n).
La décision est de 30 points : on trie le dernier point lié à la première partie de la constance des deux, pour une partition fixe on calcule la SSE et sélectionne la optimale. De plus, il est important de ne pas oublier de démonter le boîtier lorsqu'il n'y a qu'une seule section de constance. Difficulté - O (n
2 ).
Solution pour 50 points : on trie les frontières de la division en sections de constance pour O (n
2 ), pour une partition fixe en 3 segments, on calcule le SSE et choisit le optimal. Difficulté - O (n
3 ).
La décision est de 70 points : nous calculons les sommes et les sommes des carrés des valeurs de f
i sur les préfixes, cela vous permettra de calculer rapidement la moyenne et l'ESS sur n'importe quel segment. Nous trions les limites de la partition en 4 sections de constance pour O (n
3 ), en utilisant les valeurs pré-calculées sur les préfixes pour O (1), nous calculons le SSE. Difficulté - O (n
3 ).
Solution complète : considérons la fonction de programmation dynamique dp [s] [i]. Il s'agit de la plus petite valeur SSE si nous approchons les premières valeurs i à l'aide de s segments. Alors
dp [0] [0] = 0, et pour tous les autres ensembles de paramètres, nous fixons la valeur égale à l'infini afin de minimiser davantage cette valeur. Nous allons résoudre le problème en augmentant progressivement la valeur de l'art. Comment calculer dp [s] [i] si les valeurs dynamiques pour tous les s plus petits sont déjà calculées? Il suffit de désigner pour t le nombre de premiers points couverts par les segments précédents (s - 1), de trier toutes les valeurs de t et d'approximer les points (i - t) restants en utilisant le segment restant. Il est nécessaire de choisir la meilleure valeur t pour l'ESS finale à i points. Si nous calculons les sommes et les sommes des carrés des valeurs de f
i sur les préfixes, alors cette approximation sera effectuée dans O (1), et la valeur dp [s] [i] peut être calculée dans O (n). La réponse finale est dp [k] [n]. La complexité totale de l'algorithme est O (kn
2 ).
Code de solution complet:
n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n])
C. Prédiction des clics des utilisateurs
Condition
L'un des signaux les plus importants pour un système de recommandation est le comportement de l'utilisateur. , .
..
2 : (train.csv) (test.csv). , . :
— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .
.
, item, publisher, user, topic .
csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.
logloss.
150 . logloss :
logloss . 2 , logloss 4 .
/train.csv:
test.csv:
:
Remarques
:
yadi.sk/d/pVna8ejcnQZK_A . , .
logloss :
EPS = 1e-4
def logloss(y_true, y_pred):
if abs (y_pred - 1) < EPS:
y_pred = 1 - EPS
if abs (y_pred) < EPS:
y_pred = EPS
return -y_true ∗ log(y_pred) - (1 - y_true) ∗ log(1 - y_pred)logloss logloss .
logloss :
def score(logloss):
if logloss > 0.5:
return 0.0
return min(150, (200 ∗ (0.5 - logloss)) ∗∗ 2) , . . , (, , , ) , — , - , .
, 100 ( 150).
— CatBoost . CatBoost ( ), . , . , -:
( ) , , , , - ( ).
. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).
,
ML- .