Couche convolutionnelle: convolution rapide selon la méthode de Shmuel Vinograd

Présentation

Cet article est la suite d'une série d'articles décrivant les algorithmes sous-jacents.
Synet est un framework pour lancer des réseaux neuronaux pré-entraînés sur le CPU.

Dans un article précédent , j'ai décrit des méthodes basées sur la multiplication matricielle. Ces méthodes avec un effort minimal peuvent atteindre dans de nombreux cas plus de 80% du maximum théorique. Il semblerait, eh bien, où pouvons-nous encore l'améliorer? Il s'avère que vous le pouvez! Il existe des méthodes mathématiques qui peuvent réduire le nombre d'opérations requises pour la convolution. Nous allons nous familiariser avec l'une de ces méthodes, l'algorithme de convolution par la méthode Vinograd, dans cet article.


Shmuel Winograd 1936.01.04 - 2019.03.25 - Un remarquable informaticien israélien et américain, créateur d'algorithmes pour la multiplication matricielle rapide, la convolution et la transformation de Fourier.

Un peu de maths

Bien que, dans l'apprentissage automatique, les convolutions à noyau carré soient le plus souvent utilisées, afin de simplifier la présentation, nous considérerons d'abord le cas unidimensionnel. Supposons que nous ayons une image d'entrée unidimensionnelle de taille $$$1 \ fois4$:

$$

$$d = \ begin {bmatrix} d_0 & d_1 & d_2 & d_3 \ end {bmatrix} ^ T,$$

et la taille du filtre $$$1 \ fois3$:

$$

$$g = \ begin {bmatrix} g_0 & g_1 & g_2 \ end {bmatrix} ^ T,$$

alors le résultat de la convolution sera:

$$

$$F (2,3) = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix}.$$

Ces expressions seront facilement réécrites sous forme matricielle:

$$

$$F (2,3) = \ begin {bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \ end {bmatrix} \ begin {bmatrix} g_0 \\ g_1 \\ g_2 \ end {bmatrix} = \ begin {bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \ end {bmatrix} = \ begin {bmatrix} m_1 + m_2 + m_3 \\ m_2 - m_3 - m_4 \ end {bmatrix}, (1)$$

où la notation est utilisée:

$$

$$m_1 = (d_0-d_2) g_0, \\ m_2 = (d_1 + d_2) \ frac {g_0 + g_1 + g_2} {2}, \\ m_3 = (d_2-d_1) \ frac {g_0-g_1 + g_2} {2}, \\ m_4 = (d_1-d_3) g_2.$$

À première vue, le dernier remplacement semble quelque peu inutile - il y a clairement plus d'opérations. Mais les expressions $$$\ frac {g_0 + g_1 + g_2} {2}$et $$$\ frac {g_0-g_1 + g_2} {2}$ne doit être calculé qu'une seule fois. Dans cet esprit, nous devons effectuer seulement 4 opérations de multiplication, tandis que dans la formule d'origine, elles doivent être effectuées 6.
On réécrit l'expression (1):

$$

$$F (2,3) = A ^ T [(G g) \ odot (B ^ T d)], (2)$$

où $$$\ odot$dénote la multiplication par élément, et la notation suivante est également utilisée:

$$

$$B ^ T = \ begin {bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \ end { bmatrix}, (3) \\ G = \ begin {bmatrix} 1 & 0 & 0 \\ \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {2} \\ \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {2} \\ 0 & 0 & 1 \ end {bmatrix}, (4) \\ A ^ T = \ begin {bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \ end {bmatrix}. (5)$$

L'expression (2) peut être généralisée au cas bidimensionnel:

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A. (6)$$

Le nombre requis d'opérations de multiplication pour $$$F (2 \ fois2,3 \ fois3)$reculer de $$$2 \ times2 \ times3 \ times3 = 36$avant $$$4 \ times4 = 16$. Ainsi, nous obtenons le gain de calcul $$$\ frac {36} {16} = 2,25$fois. Si vous visualisez, alors en fait nous, au lieu de calculer séparément la convolution pour chaque point d'image, nous la calculerons immédiatement pour un bloc de taille $$$2 \ fois2$:

Dans tous les cas, pour convolution avec la fenêtre $$$r \ fois s$et la taille du bloc $$$m \ fois n$le nombre de multiplications nécessaires sera

$$

$$count = (m + r - 1) \ times (n + s - 1), (7)$$

et le gain est décrit par la formule:

$$

$$k = \ frac {m \ times n \ times r \ times s} {(m + r - 1) \ times (n + s - 1)}. (8)$$

Dans la limite, pour suffisamment grand $$$m$et $$$n$pour toute convolution, 1 seule opération de multiplication par point suffit! Malheureusement, une augmentation de la taille des blocs entraîne une augmentation rapide des frais généraux d'entrée $$$B ^ T d B$et week-end $$$A ^ T [...] A$images, donc dans la pratique, n'utilisez généralement pas une taille de bloc supérieure à $$$4 \ fois4$.

Exemple d'implémentation

Pour l'implémentation pratique de l'algorithme de Vinograd, je voudrais considérer le cas le plus simple - la convolution avec le noyau $$$3 \ fois3$pour bloc $$$2 \ fois2$. Afin de simplifier davantage la présentation, nous supposerons également qu'il n'y a pas de remplissage de l'image d'entrée et que les tailles des images d'entrée et de sortie sont des multiples de 2.

L'implémentation de convolution basée sur la multiplication matricielle ressemblera à:

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Ceux qui veulent comprendre en détail ce qui se passe ici devraient consulter mon article précédent . L'implémentation actuelle est obtenue à partir de la précédente, si l'on met:

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

Algorithme de convolution modifié

Je redonne ici la formule (6):

$$

$$F (2 \ times2,3 \ times3) = A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

Si vous passez de la taille de l'image de sortie $$$2 \ fois2$à une image de taille arbitraire, alors nous devons la diviser en blocs de taille $$$2 \ fois2$. Pour chacun de ces blocs, une image d'entrée sera formée $$$(2 + 3 - 1) \ fois (2 + 3 - 1) = 16$valeurs incluses dans 16 convertis $$$B ^ T d B$images d'entrée réduites de moitié. Ensuite, chacune de ces 16 matrices est multipliée par la matrice correspondante des poids transformés $$$G g G ^ T$. 16 matrices résultantes sont converties en image de sortie $$$A ^ T \ bigg [... \ bigg] A$. Ci-dessous ce processus est dessiné dans le diagramme:



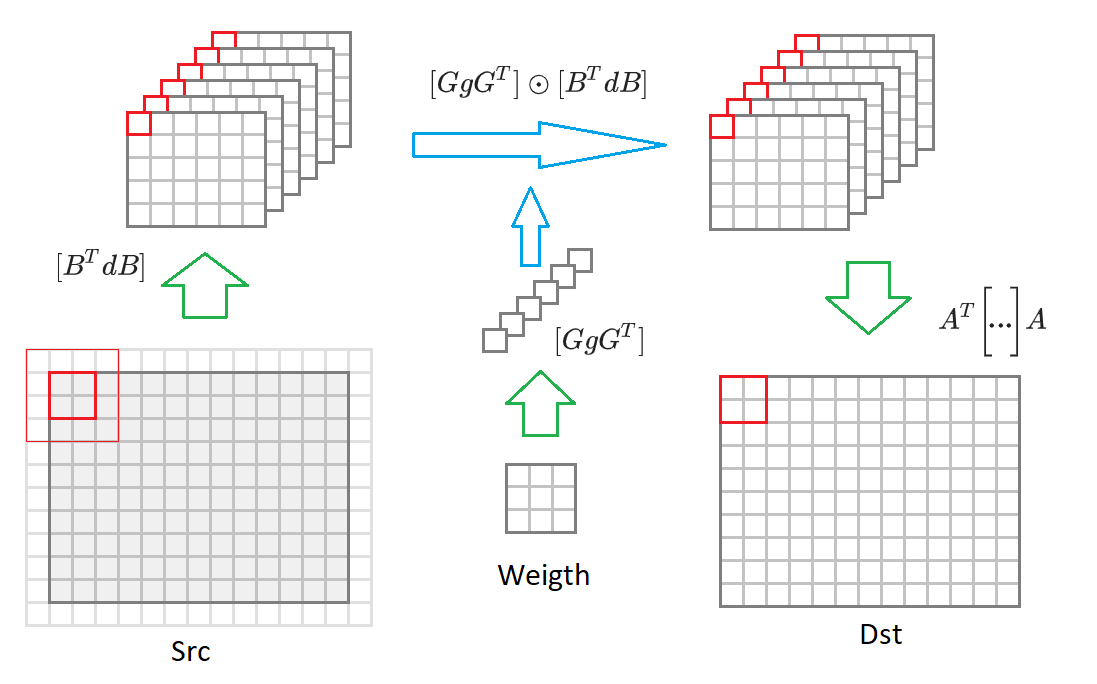
Compte tenu de ces commentaires, l'algorithme de convolution prend la forme:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Nombre d'opérations nécessaires sans tenir compte des transformations de l'image d'entrée et de sortie: ~ srcC * dstC * dstH * dstW * count . Ensuite, nous décrivons les algorithmes de conversion des poids, des images d'entrée et de sortie.

Convertir des échelles convolutionnelles

Comme le montre l'expression (6), la transformation suivante doit être effectuée sur les poids de convolution: $$$G g G ^ T$où est la matrice $$$G$défini dans l'expression (4). Le code de cette conversion ressemblera à ceci:

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

Heureusement, cette conversion ne doit être effectuée qu'une seule fois. Par conséquent, cela n'affecte pas les performances finales.

Conversion d'image d'entrée

Comme le montre l'expression (6), la transformation suivante doit être effectuée sur l'image d'entrée: $$$B ^ T d B$où est la matrice $$$B ^ T$défini dans l'expression (3). Le code de cette conversion ressemblera à ceci:

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

Le nombre d'opérations requises pour cette conversion est: ~ srcH * srcW * srcC * count .

Conversion d'image de sortie

Comme le montre l'expression (6), la transformation suivante doit être effectuée sur l'image de sortie: $$$A ^ T [...] A$où est la matrice $$$B ^ T$défini dans l'expression (5). Le code de cette conversion ressemblera à ceci:

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

Le nombre d'opérations requises pour cette conversion est: ~ dstH * dstW * dstC * count .

Caractéristiques de la mise en œuvre pratique

Dans l'exemple ci-dessus, nous avons décrit l'algorithme de Vinohrad pour un bloc de taille $$$2 \ fois2$. En pratique, une version plus avancée de l'algorithme est le plus souvent utilisée: $$$F (4 \ fois4,3 \ fois3)$. Dans ce cas, la taille du bloc sera $$$4 \ fois4$et le nombre de matrices transformées est de 36. Le gain de calcul, selon la formule (8), atteindra 4 . Le schéma général de l'algorithme est le même, seule la matrice des algorithmes de transformation diffère.

Il existe un petit projet sur Github qui vous permet de calculer ces matrices avec des coefficients pour une taille de noyau de convolution arbitraire et une taille de bloc.

Nous avons présenté une variante de l'algorithme Vinograd pour le format d' image NCHW , mais l'algorithme peut être implémenté de manière similaire pour le format NHWC (j'ai parlé plus en détail de ces formats d'image dans l' article précédent .

Malgré la présence de transformations supplémentaires, la principale charge de calcul dans l'algorithme de Vinograd (avec son application compétente, bien sûr) réside toujours dans la multiplication matricielle. Heureusement, il s'agit d'une opération standard et est effectivement implémentée dans de nombreuses bibliothèques.

Les fonctions de transformation optimisées pour différentes plates-formes pour l'algorithme Vinohrad peuvent être trouvées ici .

Avantages et inconvénients de l'algorithme de raisin

Tout d'abord, bien sûr, les pros:

• L'algorithme permet plusieurs fois (le plus souvent 2-3 fois) d'accélérer le calcul de la convolution. Ainsi, il est possible de calculer la convolution plus rapidement que la limite "théorique".
• L'algorithme repose dans sa mise en œuvre sur l'algorithme de multiplication matriciel standard.
• Il peut être implémenté pour différents formats d'image d'entrée: NCHW , NHWC .
• La taille de la mémoire tampon pour le stockage des valeurs intermédiaires est inférieure à celle requise pour l'algorithme de multiplication matricielle.

Eh bien et où sans inconvénients:

• L'algorithme nécessite une implémentation distincte des fonctions de conversion pour chaque taille de noyau de convolution, ainsi que pour chaque taille de bloc. C'est peut-être l'une des principales raisons pour lesquelles il est presque partout implémenté uniquement pour la convolution avec le noyau. $$$3 \ fois3$.
• À mesure que la taille des blocs augmente, la complexité de la mise en œuvre des fonctions de conversion augmente rapidement. Par conséquent, il n'y a pratiquement aucune implémentation avec une taille de bloc supérieure à $$$4 \ fois4$.
• L'algorithme impose des restrictions strictes sur les paramètres de convolution strideY = strideY = dilationY = dilationX = group = 1 . Bien que théoriquement, il soit possible de mettre en œuvre l'algorithme lorsque ces restrictions sont violées, en pratique, il est peu applicable en raison d'une faible efficacité.
• L'efficacité de l'algorithme diminue si le nombre de canaux d'entrée ou de sortie dans l'image est petit (cela est dû au coût de conversion des images d'entrée et de sortie).
• L'efficacité de l'algorithme diminue pour les petites tailles d'images d'entrée (les matrices résultantes de l'image d'entrée sont trop petites et l'algorithme de multiplication matriciel standard devient inefficace pour elles).

Conclusions

La méthode de calcul de convolution basée sur l'algorithme de Vinograd peut augmenter considérablement l'efficacité de calcul par rapport à la méthode basée sur une simple multiplication matricielle. Malheureusement, il n'est pas universel et assez difficile à mettre en œuvre. Pour un certain nombre de cas particuliers, il existe des approches plus rapides, dont je voudrais reporter la description pour les prochains articles de cette série . En attente de commentaires et de commentaires des lecteurs. J'espère que vous étiez intéressé!

PS Cette approche et d'autres sont implémentées par moi dans le cadre de convolution dans le cadre de la bibliothèque Simd .
Ce cadre sous-tend Synet , un cadre pour exécuter des réseaux de neurones pré-formés sur le CPU.