Les méthodes de Newton-Cotes sont une combinaison de techniques d'intégration approximatives basées sur:
- diviser l'intervalle d'intégration en intervalles égaux;
- approximations de l'intégrande sur des intervalles sélectionnés par des polynômes;
- trouver l'aire totale du trapèze courbe obtenu.
Cet article couvrira plusieurs méthodes de Newton-Cotes:
- méthode trapézoïdale;
- La méthode de Simpson;
- Méthode Romberg.
Méthode trapézoïdale
La méthode trapézoïdale est la plus simple de celles considérées. À titre d'exemple, prenez l'intégrale suivante:
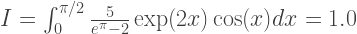
La précision de l'approximation dépend du nombre N de segments dans lesquels l'intervalle d'intégration est divisé. Ainsi, la longueur de l'écart:
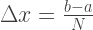
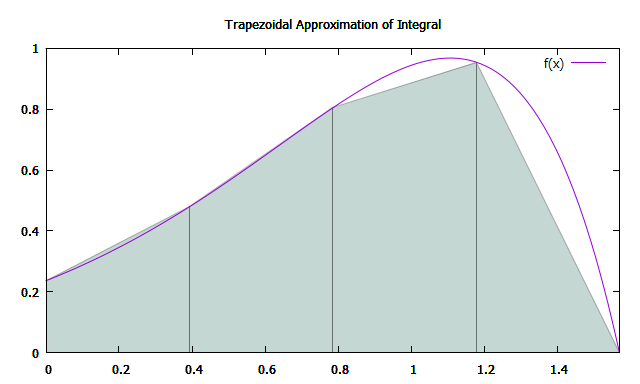
L'aire du trapèze peut être calculée par la formule:
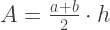
En résumant tout ce qui précède, la valeur approximative de l'intégrale est calculée par la formule:
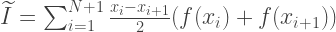
La fonction qui calcule l'intégrale par la méthode trapézoïdale doit prendre 4 paramètres:
- limites du segment d'intégration;
- fonction integrand;
- le nombre N d'intervalles de la partition.
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; }
Méthode Simpson
La méthode Simpson consiste à intégrer le polynôme d'interpolation au deuxième degré de la fonction f (x) avec les nœuds d'interpolation a, b et m = (a + b) / 2 - paraboles p (x) .Pour augmenter la précision, il est logique de diviser le segment d'intégration en N intervalles égaux ( par analogie avec la méthode trapézoïdale), sur chacune desquelles appliquer la méthode Simpson.
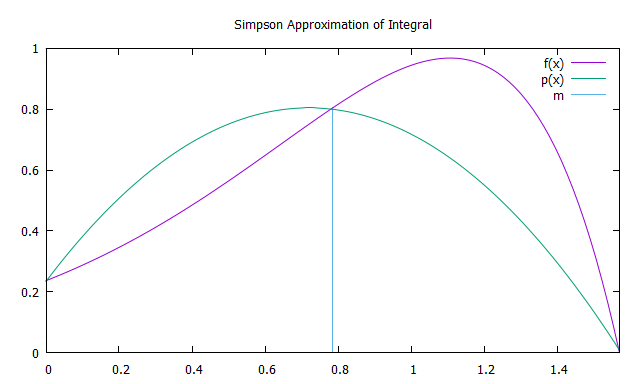
L'aire de la parabole peut être trouvée en additionnant les aires de 6 rectangles d'égale largeur. La hauteur du premier d'entre eux doit être égale à f (a), du troisième au cinquième - f (m), le sixième - f (m). Ainsi, l'approximation par la méthode Simpson est trouvée par la formule:
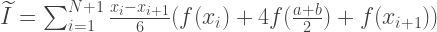
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double simpson_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2)); } return simpson_integral; }
Méthode Romberg
Soit T (x) l'approximation intégrale obtenue par la méthode trapézoïdale à l'étape x. Nous obtenons 3 approximations de ce type, réduisant la taille du pas de 2 fois à chaque calcul.

Nous construisons maintenant une parabole symétrique par rapport à l'axe y, passant par les points T (1) et T (1/2) afin d'extrapoler les valeurs obtenues pour x tendant vers 0.
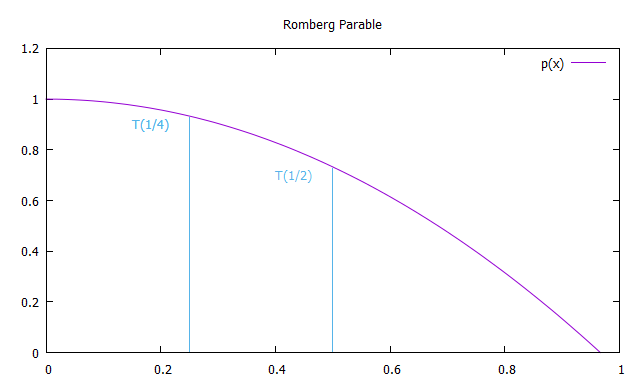
Par conséquent, chaque membre de la première colonne R (n, 0) des approximations de Romberg est équivalent aux solutions obtenues par la méthode trapézoïdale, et chaque solution de la deuxième colonne de R (n, 1) est équivalente à la méthode Simpson. Ainsi, les formules d'intégration approximative par la méthode de Romberg:
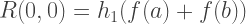
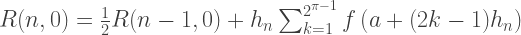
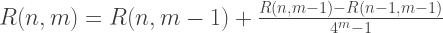
Implémentation C ++:
std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) { std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n)); romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f); double h = ba; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h; for(size_t rbStep = 1; rbStep <= step; rbStep++) { const double k = pow(4, rbStep); romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1); } } return romberg_integral; }