Lors de l'extraction d'informations, la tâche se pose souvent de trouver de tels fragments de texte. Dans le cadre d'une recherche, une requête peut être générée par l'utilisateur (par exemple, le texte que l'utilisateur saisit dans le moteur de recherche) ou par le système lui-même. Souvent, nous devons faire correspondre une requête entrante avec des requêtes déjà indexées. Dans cet article, nous verrons comment vous pouvez créer un système qui résout ce problème par rapport à des milliards de demandes sans dépenser une fortune sur l'infrastructure du serveur.

Tout d'abord, nous définissons formellement le problème:

Étant donné un ensemble fixe de requêtes $$$Q$ demande entrante $$$q$ et entier $$$k$ . Besoin de trouver un tel sous-ensemble de requêtes $$$R = \ left \ {q0, q1, ..., qk \ right \} \ sous-ensemble Q$ à chaque demande $$$q_ {i} \ en R$ était plus comme $$$q$ que toute autre demande $$$Q ∖ R$ .

Par exemple, avec cet ensemble de requêtes $$$Q$ :

{tesla cybertruck, beginner bicycle gear, eggplant dishes, tesla new car, how expensive is cybertruck, vegetarian food, shimano 105 vs ultegra, building a carbon bike, zucchini recipes} 

et $$$k = 3$ Vous pouvez vous attendre à ce résultat:


Veuillez noter que nous n'avons pas encore défini de critère de similitude . Dans ce contexte, cela peut signifier presque n'importe quoi, mais cela se résume généralement à une certaine forme de similitude basée sur des mots clés ou des vecteurs. En utilisant la similitude basée sur les mots clés, nous pouvons trouver deux requêtes similaires si elles contiennent suffisamment de mots communs. Par exemple, les requêtes «ouverture d'un restaurant à munich» et «meilleur restaurant de munich» sont similaires car elles contiennent les mots «restaurant» et «munich». Et les requêtes «meilleur restaurant de munich» et «où manger à munich» sont déjà moins similaires, car elles n'ont qu'un seul mot commun. Cependant, quelqu'un qui cherche un restaurant à Munich serait mieux si la deuxième paire de demandes s'avérait similaire. Et en cela, nous allons aider la comparaison basée sur des vecteurs.

Représentation vectorielle des mots

La représentation vectorielle des mots est une technique d'apprentissage automatique utilisée dans le traitement du langage naturel pour convertir du texte ou des mots en vecteurs. Déplacer la tâche dans l'espace vectoriel, nous pouvons utiliser des opérations mathématiques avec des vecteurs - additionner et calculer les distances. Pour établir des liens entre des mots similaires, vous pouvez utiliser des méthodes traditionnelles de regroupement vectoriel. La signification de ces opérations dans l'espace de mots d'origine n'est peut-être pas évidente, mais l'avantage est que nous avons maintenant accès à un large éventail d'outils mathématiques. Si vous êtes intéressé par des détails sur les vecteurs de mots et leur application, lisez à propos de word2vec et GloVe .

Nous avons un moyen de générer des vecteurs à partir de mots, nous allons maintenant les collecter en vecteurs de texte (vecteurs de documents ou d'expressions). La façon la plus simple de le faire est d'ajouter (ou de faire la moyenne) les vecteurs de tous les mots du texte.


^{Figure 1: vecteurs de requête.}

Vous pouvez maintenant déterminer la similitude de deux morceaux de texte (ou requêtes) en les représentant dans l'espace vectoriel et en calculant la distance entre les vecteurs. En règle générale, une distance angulaire est utilisée pour cela.

Par conséquent, la représentation vectorielle des mots permet une correspondance textuelle d'un type différent, qui complète la correspondance basée sur des mots clés. Vous pouvez explorer la similitude sémantique des demandes (par exemple, "meilleur restaurant de munich" et "où manger à munich"), comme nous ne pouvions pas le faire auparavant.

Recherche approximative du voisin le plus proche

Maintenant, nous pouvons affiner notre problème de correspondance de requête d'origine:

Étant donné un ensemble fixe de vecteurs de requête $$$Q$ vecteur entrant $$$q$ et entier $$$k$ . Vous devez trouver un tel sous-ensemble de vecteurs $$$R = \ left \ {q0, q1, ..., qk \ right \} \ sous-ensemble Q$ de sorte que la distance angulaire de $$$q$ à chaque vecteur $$$q_ {i} \ en R$ était plus courte que la distance à tout autre vecteur $$$Q ∖ R$ .

C'est ce qu'on appelle la tâche de trouver le plus proche voisin. Il existe un certain nombre d'algorithmes pour sa solution rapide dans les espaces de faible dimension. Mais lorsque nous travaillons avec des représentations vectorielles de mots, nous opérons généralement avec des vecteurs de haute dimension (100-1000 dimensions). Et ici, les méthodes mentionnées ne fonctionnent plus.

Il n'existe aucun moyen approprié de déterminer rapidement les voisins les plus proches dans des espaces de grande dimension. Par conséquent, nous simplifions le problème en permettant l'utilisation de résultats approximatifs: au lieu de toujours renvoyer les vecteurs les plus proches, nous nous contenterons seulement de certains des voisins les plus proches ou dans une certaine mesure proches. C'est ce qu'on appelle la recherche approximative de la tâche des voisins les plus proches et c'est un domaine de recherche active.

Petit monde hiérarchique

Le graphique hiérarchique du petit monde navigable ( HNSW ) est l'un des algorithmes les plus rapides pour la recherche approximative des voisins les plus proches. L'index de recherche dans HNSW est une structure à plusieurs niveaux dans laquelle chaque niveau est un graphe de proximité. Chaque nœud de graphe correspond à l'un des vecteurs de requête.


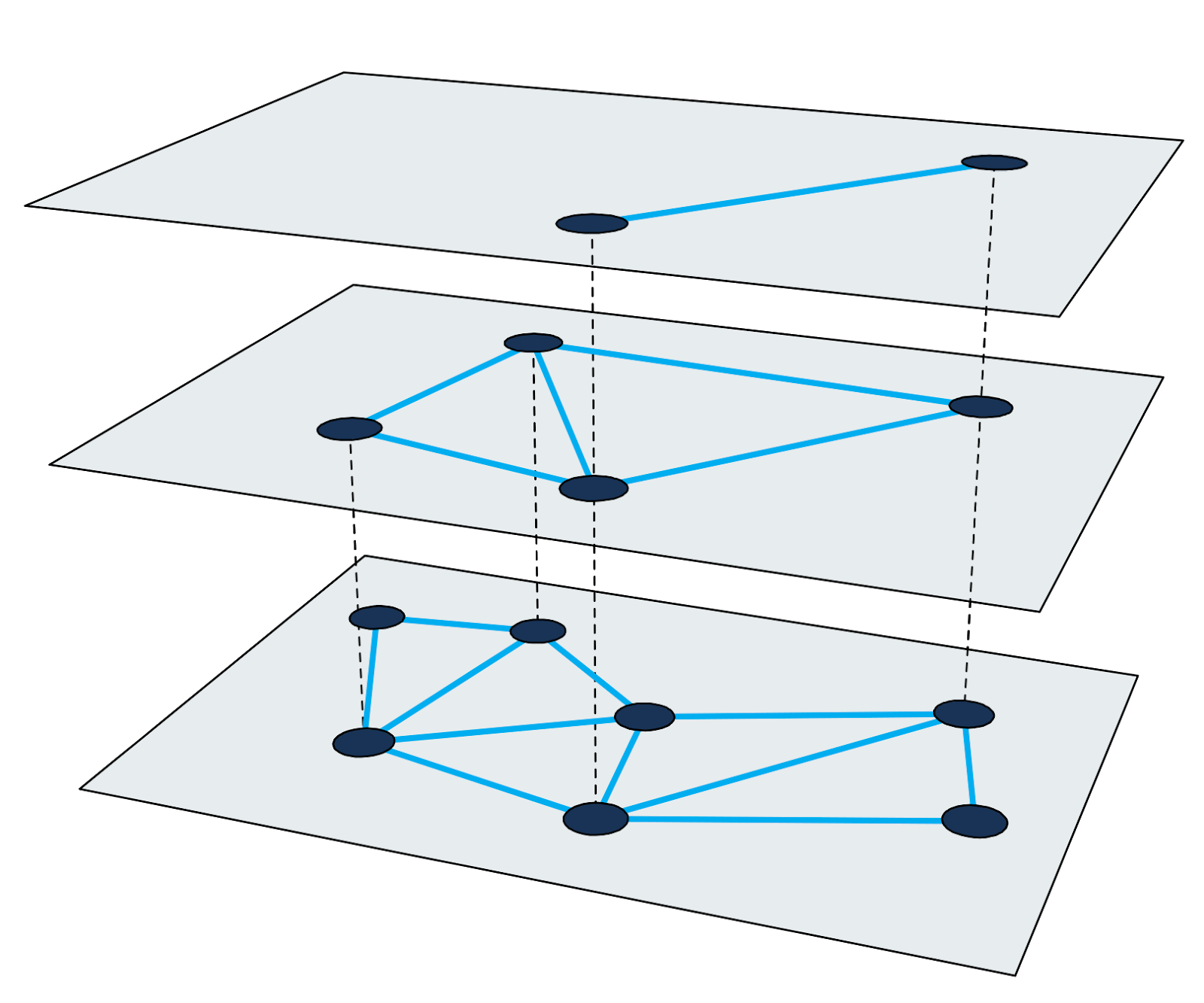^{Figure 2: Graphique de proximité à plusieurs niveaux.}
La recherche de voisins les plus proches dans HNSW utilise la méthode de zoom avant. Il commence dans le nœud d'entrée du plus haut niveau et effectue récursivement une traversée de graphe gourmande à chaque niveau jusqu'à ce qu'il atteigne un minimum local en bas.

Les détails sur l'algorithme et la technique de recherche sont bien décrits dans les travaux scientifiques. Il est important de se rappeler que chaque cycle de recherche des voisins les plus proches consiste à parcourir les nœuds des graphes avec calcul des distances entre les vecteurs. Nous examinerons ces étapes ci-dessous pour utiliser cette méthode pour créer un index à grande échelle.

La difficulté d'indexer des milliards de requêtes

Supposons que nous devons indexer 4 milliards de vecteurs de requête à 200 dimensions, chaque dimension étant représentée par un nombre à virgule flottante de quatre octets (4 milliards suffisent pour rendre la tâche intéressante, mais vous pouvez toujours stocker les ID de nœud dans des nombres normaux à quatre octets) . Un calcul approximatif nous indique que la taille des vecteurs seuls sera d'environ 3 To. Comme la plupart des bibliothèques existantes utilisent une capacité RAM pour une recherche approximative des voisins les plus proches, nous aurons besoin d'un très grand serveur pour pousser au moins des vecteurs dans la RAM. Veuillez noter que cela ne prend pas en compte l'index de recherche supplémentaire, qui est nécessaire pour la plupart des méthodes.

Dans toute l'histoire du développement de notre moteur de recherche, nous avons utilisé plusieurs approches différentes pour résoudre ce problème. Examinons certains d'entre eux.

Sous-ensemble de données

La première et la plus simple approche, qui ne nous a pas permis de résoudre complètement le problème, a été de limiter le nombre de vecteurs dans l'indice. En prenant un dixième des données, nous avons créé un index qui nécessite - surprise - 10% de mémoire. Cependant, la qualité de la recherche s'est détériorée, car nous avons maintenant opéré avec moins de requêtes.

Quantification

Ici, nous avons utilisé toutes les données, mais nous les avons réduites en utilisant la quantification (nous avons utilisé différentes techniques de quantification, par exemple, la quantification des produits, mais nous n'avons pas pu atteindre la qualité de travail souhaitée avec cette quantité de données). En arrondissant certaines erreurs, nous avons pu remplacer tous les nombres à quatre octets dans les vecteurs d'origine par des versions quantifiées à un octet. La quantité de RAM pour les vecteurs a diminué de 75%. Cependant, nous avions encore besoin de 750 Go de mémoire (sans compter la taille de l'index lui-même), et c'est toujours un très grand serveur.

Résolution des problèmes de mémoire avec Granne

Les approches décrites avaient leurs avantages, mais elles nécessitaient beaucoup de ressources et donnaient une mauvaise qualité de recherche. Bien qu'il existe des bibliothèques qui répondent en moins de 1 ms, nous pourrions sacrifier la vitesse en échange d'exigences matérielles plus faibles.

Granne (graphique-based voisins les plus proches) est une bibliothèque HNSW développée et utilisée par Cliqz pour rechercher de telles requêtes. Il a du code open source, mais la bibliothèque est toujours en développement actif. Une version améliorée sera publiée sur crates.io en 2020. Il est écrit en rouille avec des inserts en Python, conçu pour gérer des milliards de vecteurs en utilisant la compétitivité. Du point de vue des vecteurs de requête, il est intéressant de noter que Granne dispose d'un mode spécial qui nécessite beaucoup moins de mémoire par rapport aux autres bibliothèques.

Représentation compacte des vecteurs de requête

Réduire la taille des vecteurs de requête nous apportera de nombreux avantages. Pour ce faire, revenons en arrière et envisageons de créer des vecteurs. Étant donné que les requêtes sont composées de mots et que les vecteurs de requête sont des sommes de vecteurs de mots, nous pouvons explicitement refuser de stocker des vecteurs de requête et les calculer si nécessaire.

Vous pouvez stocker des requêtes sous forme d'ensembles de mots et utiliser la table de recherche pour trouver les vecteurs correspondants. Cependant, nous évitons la redirection en stockant chaque requête sous la forme d'une liste d'ID entiers correspondant aux vecteurs de mots dans la requête. Par exemple, enregistrez la requête «meilleur restaurant de munich» sous $$$[{i_ {best}}, {i_ {restaurant}}, {i_ {of}}, {i_ {munich}}]$ où $$${i_ {best}}$ - c'est l'ID de vecteur du mot «meilleur», etc. Supposons que nous ayons moins de 16 millions de vecteurs de mots (plus que ce montant coûtera 1 octet par mot), alors vous pouvez utiliser 3 octets pour représenter tous les ID de mot. Autrement dit, au lieu de stocker 800 octets (ou 200 octets dans le cas de vecteurs quantifiés), nous ne stockerons que 12 octets pour cette demande (ce n'est pas tout à fait vrai. Comme les demandes se composent d'un nombre différent de mots, nous devons également stocker l'offset de la liste dans l'index des mots. Pour cela nécessitera 5 octets par demande).

Quant aux vecteurs de mots, nous en avons tous besoin. Cependant, le nombre de mots est beaucoup plus petit que le nombre de requêtes pouvant être créées en combinant ces mots. Et cela signifie que la taille des mots n'est pas si importante. Si vous stockez des vecteurs de mots sous forme de versions à virgule flottante de quatre octets dans un tableau simple $$$v$ , nous avons besoin de moins de 1 Go pour chaque million de mots. Ce volume peut facilement tenir dans la RAM. Maintenant, le vecteur de requête ressemble à ceci: $$${v _ {{i_ {best}}}} + {v _ {{i_ {restaurant}}} + {v _ {{i_ {of}}} + {v _ {{i_ {munich}}}}}$ .

La taille finale de la soumission de la requête dépend du nombre total de mots dans la requête. Pour 4 milliards de requêtes, cela représente environ 80 Go (y compris les vecteurs de mots). En d'autres termes, par rapport aux vecteurs de mots d'origine, la taille a diminué de 97% et par rapport aux vecteurs quantifiés - de 90%.

Et encore une chose. Pour une recherche, nous devons visiter environ 200-300 nœuds du graphique. Chaque nœud a 20 à 30 voisins. Donc, nous devons calculer la distance entre le vecteur de requête d'entrée et les vecteurs 4000-9000 dans l'index. Et de plus, nous devons générer des vecteurs. Combien de temps faut-il pour créer des vecteurs de requête à la volée?

Il s'avère qu'avec un processeur assez récent, ce problème peut être résolu en quelques millisecondes. Une requête qui s'exécutait en 1 ms s'exécute maintenant en 5 ms environ. Mais ensuite, nous avons réduit la quantité de mémoire pour les vecteurs de 90%. Nous avons accepté avec plaisir un tel compromis.

Affichage en mémoire des vecteurs et index

Ci-dessus, nous avons résolu le problème de la réduction de la quantité de mémoire pour les vecteurs. Mais après avoir résolu ce problème, la structure de l'indice elle-même est devenue un facteur limitant. Vous devez maintenant réduire sa taille.

À Granne, la structure du graphe est stockée de manière compacte sous la forme d'une liste d'adjacence avec un nombre variable de voisins pour chaque nœud. Autrement dit, la mémoire n'est guère gaspillée en métadonnées. La taille de la structure d'index dépend en grande partie des paramètres de conception et des propriétés du graphique. Néanmoins, pour avoir une idée de la taille de l'index, il suffit de dire que nous pouvons construire un index pour 4 milliards de vecteurs avec une taille totale d'environ 240 Go. Cela peut être acceptable pour une utilisation en mémoire sur un grand serveur, mais cela peut être mieux fait.


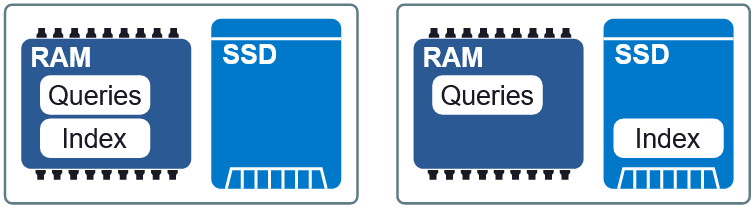^{Figure 3: Deux dispositions différentes en RAM et SSD.}

Une propriété importante de Granne est la possibilité d' afficher les vecteurs d'index et de requête en mémoire . Cela nous permet de charger l'index paresseusement et de partager la mémoire avec plusieurs processus. Les fichiers d'index et de requête sont divisés en fichiers d'affichage distincts en mémoire et peuvent être utilisés dans différentes dispositions en RAM et sur SSD. Si les exigences pour le délai sont légèrement plus faibles, alors en plaçant l'index sur le SSD, les requêtes en RAM, nous maintenons une vitesse acceptable sans consommation excessive de mémoire. À la fin de l'article, nous verrons à quoi ressemble ce compromis.

Amélioration de la localisation des données

Dans notre configuration actuelle, lorsque l'index est sur un SSD, chaque demande nécessite jusqu'à 200-300 lectures à partir du disque. Vous pouvez essayer d'augmenter la localité des données en disposant les éléments dont les vecteurs sont si proches que leurs nœuds HNSW sont situés dans l'index également non loin les uns des autres. La localisation des données améliore les performances, car une seule opération de lecture (généralement extraite de 4 Ko) est plus susceptible de contenir d'autres nœuds nécessaires pour parcourir le graphique. Et cela, à son tour, réduit le nombre de récupérations de données par recherche.


^{Figure 4: La localisation des données réduit la récupération d'informations.}

Il convient de noter que la réorganisation des éléments n'affecte pas les résultats de la recherche, c'est une façon de l'accélérer. Autrement dit, l'ordre peut être quelconque, mais toutes les options n'accélèrent pas la recherche. Il est très difficile de trouver l'ordre optimal. Cependant, l'heuristique que nous avons utilisée avec succès est de trier les requêtes par le mot le plus important dans chaque requête.

Conclusion

Nous utilisons Granne pour créer et maintenir des index de plusieurs milliards de dollars avec des vecteurs de requête afin de rechercher des requêtes similaires avec une consommation de mémoire relativement faible. Le tableau ci-dessous montre les exigences pour différentes méthodes. Soyez sceptique quant aux valeurs absolues des retards pendant la recherche, car ils dépendent fortement de ce qui est considéré comme une réponse acceptable. Cependant, ces informations décrivent les performances relatives des méthodes.


* L'allocation d'un index mémoire supérieur à la quantité requise a conduit à la mise en cache de certains nœuds (fréquemment visités), ce qui a réduit le retard dans la recherche. Aucun cache interne n'a été utilisé pour cela, uniquement des outils de système d'exploitation internes (noyau Linux).

Il convient de noter que certaines des optimisations mentionnées dans l'article ne sont pas applicables pour résoudre le problème général de trouver des voisins les plus proches avec des vecteurs indécomposables. Cependant, ils sont applicables dans toutes les situations où des éléments peuvent être générés à partir de moins de pièces (comme c'est le cas avec les mots et les requêtes). Sinon, vous pouvez toujours utiliser Granne avec les vecteurs sources, cela prend juste plus de mémoire, comme avec les autres bibliothèques.