Maths génériques dangereux en C #

Malheureusement, il n'a pas été facile de traduire correctement le nom de la laideur que j'ai commencé en russe. J'ai été surpris de constater que la documentation MSDN officielle appelle des «modèles» «génériques» (similaires aux modèles C++ , je suppose). Dans la 4e édition de "CLR via C# qui m'a frappé , Jeffrey Richter , traduit par Peter , les génériques sont appelés «généralisations», ce qui reflète bien mieux l'essence du concept. Cet article parlera des opérations mathématiques généralisées dangereuses en C# . Étant donné que C# pas destiné à l'informatique haute performance (bien qu'il puisse certainement, mais n'est pas en mesure de rivaliser avec le même C/C++ ), BCL ne prête pas beaucoup d'attention aux opérations mathématiques. Essayons de simplifier le travail avec les types arithmétiques de base en utilisant C# et CLR .

Énoncé du problème

Avertissement : l'article contiendra de nombreux fragments de code, dont certains que j'illustrerai avec des liens vers la merveilleuse ressource SharpLab ( Gi r tHub ) d' Andrey Shchekin .

La plupart des calculs se résument d'une manière ou d'une autre aux opérations de base. L'addition, la soustraction (inversion, négation), la multiplication et la division peuvent être complétées par des opérations de comparaison et de vérification de l'égalité. Bien sûr, toutes ces actions peuvent être facilement et simplement effectuées sur des variables de n'importe quel type arithmétique de base de C# . Le seul problème est que C# devrait savoir au moment de la compilation que les opérations sont effectuées sur des types spécifiques, et il semble que l'écriture d'une méthode qui ajoute de manière aussi efficace (et transparente) deux entiers et deux nombres à virgule flottante est impossible.

Précisons nos souhaits pour une méthode généralisée hypothétique qui effectue une opération mathématique simple:

1. Une méthode doit avoir des restrictions de type généralisées qui nous empêchent d'essayer d'ajouter (ou de multiplier, de diviser) deux types arbitraires. Nous avons besoin d'une contrainte de type générique.
2. Pour la pureté de l'expérience, les types acceptés et retournés doivent être les mêmes. Par exemple, un opérateur binaire doit avoir une signature de la forme (T, T) => T
3. La méthode doit être au moins partiellement optimisée. Par exemple, la boxe omniprésente est inacceptable.

Et les voisins?

Regardons F# . Je ne suis pas fort en F# , mais la plupart des restrictions C# sont dictées par les limitations CLR , ce qui signifie que F# souffre des mêmes problèmes. Vous pouvez essayer de déclarer une méthode d'addition généralisée explicite et la méthode d'addition habituelle et voir ce que dit le système d'inférence de type F# :

 let add_gen (x : 'a) (y : 'a) = x + y let add xy = x + y add_gen 5.0 6.0 |> ignore add 5.0 6.0 |> ignore 

Dans ce cas, les deux méthodes se révéleront non généralisées et le code généré sera identique. Étant donné la rigidité du système de type F# , où il n'y a pas de conversions implicites de la forme int -> double , après le premier appel de ces méthodes avec des paramètres de type double (en termes C# ), appelez des méthodes avec des paramètres d'autres types (même avec une possible perte de précision due à la conversion de type) plus échouera.

Il convient de noter que si vous remplacez l'opérateur + par l'opérateur d'égalité = , l' image devient quelque peu différente : les deux méthodes deviennent généralisées (du point de vue de C# ), et une méthode d'assistance spéciale disponible en F# est appelée pour effectuer la comparaison.

 let eq_gen (x : 'a) (y : 'a) = x = y let eq xy = x = y eq_gen 5.0 6.0 |> ignore eq_gen 5 6 |> ignore eq 5.0 6.0 |> ignore eq 5 6 |> ignore 

Et Java ?

Il m'est difficile de parler de Java , mais, pour autant que je sache, les types significatifs ne sont pas là sous la forme habituelle pour nous, mais il existe encore des types primitifs . Pour travailler avec les primitives en Java il existe des wrappers (par exemple, une référence Long pour la primitive par valeur long ), qui ont un Number classe de base commun. Ainsi, vous pouvez généraliser partiellement les opérations à l'aide de Number , mais il s'agit d'un type de référence, qui est peu susceptible d'avoir un effet positif sur les performances.

Corrigez-moi si je me trompe.

C++ ?

C++ est un langage pour les tricheurs.
C++ ouvre la voie à des fonctionnalités que certains considèrent ... contre nature .
Les modèles (ou modèles), contrairement aux généralisations (génériques), sont, au sens littéral, des modèles . Lors de la déclaration d'un modèle, vous pouvez restreindre explicitement les types pour lesquels ce modèle est disponible. Pour cette raison, en C++ , par exemple, le code suivant est valide:

 #include <iostream> template<typename T, std::enable_if_t<std::is_arithmetic<T>::value>* = nullptr> T Add (T left, T right) { return left + right; } int main() { std::cout << Add(5, 6) << std::endl; std::cout << Add(5.0, 6.0) << std::endl; // std::cout << Add("a", "b") << std::endl; Does not compile } 

is_arithmetic , malheureusement, autorise à la fois char et bool comme paramètres. D'un autre côté, char peut être équivalent à sbyte dans la terminologie C# , bien que les tailles réelles des types entiers dépendent de la plate-forme / du compilateur / de la phase lunaire.

Langages de frappe dynamiques

Enfin, considérons quelques langages typés dynamiquement (et interprétés ), affinés par le calcul. Dans de tels langages, la généralisation du calcul ne pose généralement pas de problèmes: si le type de paramètres est adapté à l'exécution, conditionnellement, l'addition, alors l'opération sera effectuée, sinon elle échouera avec une erreur.

En Python (3.7.3 x64):

 def add (x, y): return x + y type(add(5, 6)) # <class 'int'> type(add(5.0, 6.0)) # <class 'float'> type(add('a', 'b') # <class 'str'> 

Dans R (3.6.1 x64)

 add <- function(x, y) x + y # Or typeof() vctrs::vec_ptype_show(add(5, 6)) # Prototype: double vctrs::vec_ptype_show(add(5L, 6L)) # Prototype: integer vctrs::vec_ptype_show(add("5", "6")) # Error in x + y : non-numeric argument to binary operator 

Inversement, dans le monde C #: on restreint le type généralisé de fonction mathématique

Malheureusement, nous ne pouvons pas faire cela. En C# les types primitifs sont des types par valeur, c'est-à-dire structures qui, bien System.Object de System.Object (et System.ValueType ), n'ont pas grand-chose en commun. Une limitation naturelle et logique est celle where T : struct . À partir de C# 7.3 nous avons la contrainte where T : unmanaged , ce qui signifie que T est un , null . En plus des types arithmétiques primitifs dont nous avons besoin, char , bool , decimal , any Enum et toute structure dont tous les champs ont le même type unmanaged managé satisfont à ces exigences. C'est-à-dire ce type passera le test:

 public struct Coords<T> where T : unmanaged { public TX; public TY; } 

Ainsi, nous ne pouvons pas écrire une fonction généralisée qui accepte uniquement les types arithmétiques souhaités. D'où l' Unsafe dans le titre de l'article - nous devrons nous fier aux programmeurs utilisant notre code. Une tentative d'appeler une méthode hypothétique généralisée T Add<T>(T left, T right) where T : unmanaged conduira à des résultats imprévisibles si le programmeur passe en argument des objets d'un type incompatible.

La première expérience, naïve: dynamic

dynamic est le premier et évident outil qui peut nous aider à résoudre notre problème. Bien sûr, l'utilisation de la dynamic pour les calculs est absolument inutile - la dynamic équivalente à l' object , et les méthodes appelées avec une variable dynamic sont transformées en une réflexion monstrueuse par le compilateur. En prime - emballer / déballer nos types de valeur. Voici un exemple :

 public class Class { public static void Method() { var x = Add(5, 6); var y = Add(5.0, 6.0); } private static dynamic Add(dynamic left, dynamic right) => left + right; } 

Regardez simplement l' IL la méthode Method :

 .method public hidebysig static void Method () cil managed { // Method begins at RVA 0x2050 // Code size 53 (0x35) .maxstack 8 IL_0000: ldc.i4.5 IL_0001: box [System.Private.CoreLib]System.Int32 IL_0006: ldc.i4.6 IL_0007: box [System.Private.CoreLib]System.Int32 IL_000c: call object Class::Add(object, object) IL_0011: pop IL_0012: ldc.r8 5 IL_001b: box [System.Private.CoreLib]System.Double IL_0020: ldc.r8 6 IL_0029: box [System.Private.CoreLib]System.Double IL_002e: call object Class::Add(object, object) IL_0033: pop IL_0034: ret } // end of method Class::Method 

Chargé 5 , compressé , chargé 6 , compressé, appelé object Add(object, object) .
L'option ne nous convient évidemment pas.

La deuxième expérience, "dans le front"

Eh bien, la dynamic n'est pas pour nous, mais le nombre de nos types est fini, et ils sont connus à l'avance. Armons-nous avec un pied-de - biche de branche et notons-le: si notre type est , calculons quelque chose, sinon - voici l'exception.

 public static T Add<T>(T left, T right) where T : unmanaged { if(left is int i32Left && right is int i32Right) { // ??? } // ... throw new NotSupportedException(); } 

III, nous rencontrons ici un problème. Si vous comprenez avec quels types nous travaillons, vous pouvez également leur appliquer l'opération, puis l'intégratif conditionnel résultant doit être converti en un type inconnu T et ce n'est pas très simple. L' return (T)(i32Left + i32Right) ne se compile pas - il n'y a aucune garantie que T est int (même si nous savons que c'est le cas). Vous pouvez essayer la double conversion return (T)(object)(i32Left + i32Right) . Tout d'abord, le montant est emballé, puis il est déballé en T Cela ne fonctionnera que si les types correspondent avant l'emballage et après l'emballage. Vous ne pouvez pas emballer int , mais décompressez-le en double , même s'il existe une conversion implicite int -> double . Le problème avec ce code est la ramification géante et l'abondance de déballage des paquets, même dans des if difficiles. Cette option n'est également pas bonne.

Réflexion et métadonnées

Eh bien, jouez et ça suffit. Tout le monde sait qu'il existe des opérateurs en C# qui peuvent être remplacés. Là, il y a + , - , == != Et ainsi de suite. Tout ce que nous devons faire est de retirer une méthode statique de type T correspondant à l'opérateur, par exemple, des ajouts - c'est tout. Eh bien, oui, encore une fois quelques packages, mais pas de branchement et pas de problèmes. Le tout peut être mis en cache par le type T et généralement accélérer le processus dans tous les sens, réduisant une opération mathématique à l'appel d'une méthode de réflexion unique. Eh bien, quelque chose comme ça:

 public static T Add<T>(T left, T right) where T : unmanaged { // Simple example without cache. var method = typeof(T) .GetMethod(@"op_Addition", new [] {typeof(T), typeof(T)}) ?.CreateDelegate(typeof(Func<T, T, T>)) as Func<T, T, T>; return method?.Invoke(left, right) ?? throw new InvalidOperationException(); } 

Malheureusement, cela ne fonctionne pas . Le fait est que les types arithmétiques (mais pas decimal ) n'ont pas une telle méthode statique. Toutes les opérations sont implémentées via des opérations IL , telles que l' add . Une réflexion normale ne résout pas notre problème.

System.Linq.Expressions

La solution basée sur les Expressions est décrite sur le blog de John Skeet ici (par Marc Gravell).
L'idée est assez simple. Supposons que nous ayons un type T qui prend en charge l'opération + . Créons une expression comme celle-ci:

 (x, y) => x + y; 

Après cela, après avoir mis en cache, nous l'utiliserons. Construire une telle expression est assez facile. Nous avons besoin de deux paramètres et d'une opération. Alors écrivons-le.

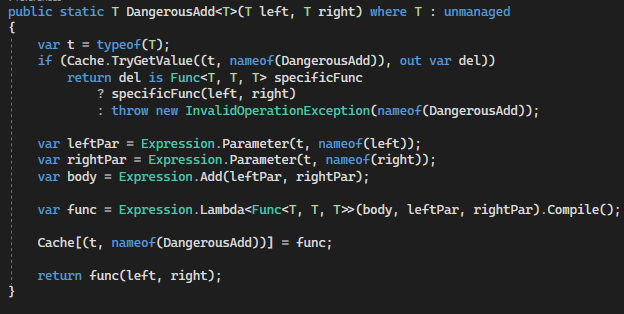
 private static readonly Dictionary<(Type Type, string Op), Delegate> Cache = new Dictionary<(Type Type, string Op), Delegate>(); public static T Add<T>(T left, T right) where T : unmanaged { var t = typeof(T); // If op is cached by type and function name, use cached version if (Cache.TryGetValue((t, nameof(Add)), out var del)) return del is Func<T, T, T> specificFunc ? specificFunc(left, right) : throw new InvalidOperationException(nameof(Add)); var leftPar = Expression.Parameter(t, nameof(left)); var rightPar = Expression.Parameter(t, nameof(right)); var body = Expression.Add(leftPar, rightPar); var func = Expression.Lambda<Func<T, T, T>>(body, leftPar, rightPar).Compile(); Cache[(t, nameof(Add))] = func; return func(left, right); } 

Des informations utiles sur les arbres d'expression et les délégués ont été publiées sur le hub

Techniquement, les expressions nous permettent de résoudre tous nos problèmes - toute opération de base peut être réduite à appeler une méthode généralisée. Toute opération plus complexe peut être écrite de la même manière, en utilisant des expressions plus complexes. C'est presque suffisant.

Nous brisons toutes les règles

Est-il possible de réaliser autre chose en utilisant la puissance de CLR/C# ? Voyons quelle année le code est généré par des méthodes d'addition pour différents types :

 public class Class { public static double Add(double x, double y) => x + y; public static int Add(int x, int y) => x + y; // Decimal only to show difference public static decimal Add(decimal x, decimal y) => x + y; } 

Le code IL correspondant contient le même ensemble d'instructions:

 ldarg.0 ldarg.1 add ret 

Il s'agit du code op très add dans lequel l'ajout de types primitifs arithmétiques est compilé. decimal à cet endroit appelle static decimal decimal.op_Addition(decimal, decimal) . Mais que se passe-t-il si nous écrivons une méthode qui sera généralisée, mais qui contient exactement ce code IL ? Eh bien, John Skeet prévient que cela n'en vaut pas la peine . Dans son cas, il considère tous les types (y compris decimal ), ainsi que leurs analogues nullable . Cela nécessitera des opérations IL tout à fait non triviales et conduira nécessairement à une erreur. Mais nous pouvons toujours essayer de mettre en œuvre des opérations de base.

À ma grande surprise, Visual Studio ne contient pas de modèles pour les projets IL et les fichiers IL . Vous ne pouvez pas simplement prendre et décrire une partie du code dans IL et l'inclure dans votre assembly. Naturellement, l'open source vient à notre aide. Le projet ILSupport contient des modèles pour les projets IL , ainsi qu'un ensemble d'instructions qui peuvent être ajoutées à *.csproj pour inclure le code IL dans le projet. Bien sûr, tout décrire en IL est assez difficile, donc l'auteur du projet utilise l'attribut MethodImpl avec l'indicateur ForwardRef . Cet attribut vous permet de déclarer la méthode comme extern et de ne pas décrire le corps de la méthode. Cela ressemble à ceci:

 [MethodImpl(MethodImplOptions.ForwardRef)] public static extern T Add<T>(T left, T right) where T : unmanaged; 

L'étape suivante consiste à écrire l'implémentation de la méthode dans le fichier *.il avec le code IL :

 .method public static hidebysig !!T Add<valuetype .ctor (class [mscorlib]System.ValueType modreq ([mscorlib]System.Runtime.InteropServices.UnmanagedType)) T>(!!T left, !!T right) cil managed { .param type [1] .custom instance void System.Runtime.CompilerServices.IsUnmanagedAttribute::.ctor() = (01 00 00 00 ) ldarg.0 ldarg.1 add ret } 

Nulle part faisant explicitement référence au type !!T , nous suggérons au CLR d'ajouter deux arguments et de renvoyer le résultat. Il n'y a pas de vérification de type et tout est dans la conscience du développeur. Étonnamment, cela fonctionne, et relativement rapidement.

Un peu de référence

Probablement, un point de repère honnête serait construit sur une expression assez complexe, dont le calcul serait comparé de front à ces dangereuses méthodes IL . J'ai écrit un algorithme simple qui résume les carrés de nombres précédemment calculés et stockés dans un double tableau et divise le montant final par le nombre de nombres. Pour effectuer l'opération, j'ai utilisé les opérateurs C# + , * et / , comme le font les personnes saines, les fonctions construites avec les Expressions et les fonctions IL .

 BenchmarkDotNet=v0.12.0, OS=Windows 10.0.18362 Intel Core i7-2700K CPU 3.50GHz (Sandy Bridge), 1 CPU, 8 logical and 4 physical cores .NET Core SDK=3.1.100 [Host] : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Job-POXTAH : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Runtime=.NET Core 3.1 

Notre code dangereux est environ 2.5 fois plus lent (en termes d'une opération). Cela peut être attribué au fait que dans le cas d'un calcul "frontal", le compilateur compile a + b dans le code d'opération add , et dans le cas d'une méthode non sûre, une fonction statique est appelée, ce qui est naturellement plus lent.

Au lieu de conclure: quand true != true

Il y a quelques jours, j'ai rencontré un tel tweet de Jared Parsons:

Il y a des cas où ce qui suit imprimera "faux"
bool b = ...
if (b) Console.WriteLine (b.IsTrue ());

C'était la réponse à cette entrée , qui montre le code de vérification bool pour true , qui ressemble à ceci:

 public static bool IsTrue(this bool b) { if (b == true) return true; else if (b == false) return false; else return !true && !false; } 

Les chèques semblent redondants, non? Jared donne un contre-exemple qui montre certaines des caractéristiques du comportement bool . L'idée est que bool est byte ( sizeof(bool) == 1 ), tandis que false correspond à 0 et true 1 . Tant que vous ne balancez pas les pointeurs, bool se comporte sans ambiguïté et de manière prévisible. Cependant, comme Jared l'a montré, vous pouvez créer un bool utilisant 2 comme valeur initiale, et une partie des vérifications échouera correctement:

 bool b = false; byte* ptr = (byte*)&b; *ptr = 2; 

Nous pouvons obtenir un effet similaire en utilisant nos opérations mathématiques dangereuses (cela ne fonctionne pas avec les Expressions ):

 var fakeTrue = Subtract<bool>(false, true); var val = *(byte*)&fakeTrue; if(fakeTrue) Assert.AreNotEqual(fakeTrue, true); else Assert.Fail("Clause not entered."); 

Oui, oui, nous vérifions à l'intérieur de la true branche si la condition est true , et nous nous attendons à ce qu'elle ne soit pas true . Pourquoi en est-il ainsi? Si vous soustrayez de 0 ( =false ) 1 ( =true ) sans vérifications, alors pour l' byte ce sera égal à 255 . Naturellement, 255 (notre fakeTrue ) n'est pas 1 (vrai true ), donc assert est exécuté. La ramification fonctionne différemment.

if inversion se produit: une branche conditionnelle est insérée; si la condition est fausse , alors une transition vers le point se produit après la fin du bloc if . La validation est effectuée par l' brfalse / brfalse_S . Il compare la dernière valeur de la pile à zéro . Si la valeur est nulle, alors elle est false , nous enjambons le bloc if . Dans notre cas, fakeTrue n'est tout simplement pas égal à zéro, donc la vérification réussit et l'exécution se poursuit à l'intérieur du bloc if , où nous comparons fakeBool avec la vraie valeur et obtenons un résultat négatif.

UPD01:
Après avoir discuté dans les commentaires avec shai_hulud et blowin , j'ai ajouté une autre méthode aux benchmarks qui implémente une branche comme if(typeof(T) == typeof(int)) return (T)(object)((int)(object)left + (int)(object)right); . Malgré le fait que JIT devrait optimiser les contrôles, au moins lorsque T est une struct , de telles méthodes fonctionnent toujours plus lentement. Il n'est pas évident si les transformations T -> int -> T optimisées, ou si la boxe / unboxing est utilisée. Les résultats de l'indice de référence MethodImpl sont MethodImpl significativement affectés par les indicateurs MethodImpl .

UPD02:
xXxVano dans les commentaires a montré un exemple d'utilisation de la ramification par type et transforme T <--> un type spécifique en utilisant Unsafe.As<TFrom, TTo>() . Par analogie avec la ramification habituelle et l' object personnalisé à travers, j'ai écrit trois opérations (addition, multiplication et division) avec ramification pour tous les types arithmétiques, après quoi j'ai ajouté une autre référence ( UnsafeBranchSum ). Malgré le fait que toutes les méthodes (sauf les expressions) génèrent du code asm presque identique (pour autant que ma connaissance limitée de l'assembleur me permette de juger), pour une raison inconnue pour moi, les deux méthodes de branchement sont très lentes par rapport à la sommation directe ( DirectSum ) et en utilisant des génériques et du code IL . Je n'ai aucune explication à cet effet, le fait que le temps passé augmente proportionnellement à N indique qu'il y a une sorte de surcharge constante pour chaque opération, malgré toute la magie du JIT . Cette surcharge est absente de la version IL des méthodes. , IL - , / / , 100% ( , ).
, , - .