Bon après-midi
Dans cet article, je vais essayer de jeter un regard neuf sur l'algorithme pour trouver une solution générale à un système d'équations linéaires.
La tâche que nous ferons ressemble à ceci.
Trouver une solution générale au système d'équations suivant
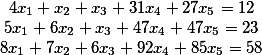
Ce problème est résolu en réduisant le système initial à une forme triangulaire selon la méthode de Gauss. Ensuite, en choisissant des variables libres, la solution générale est calculée.
Je veux montrer comment on peut résoudre de tels systèmes d'une autre manière. Pour autant qu'il soit connu et appliqué ailleurs, je n'ai pas pu le savoir. Dans tous les matériaux publics / populaires, la méthode de Gauss est utilisée.
Je dois dire tout de suite que la solution n'est certainement pas optimale (en termes de vitesse), car lors du calcul d'un produit vectoriel, il faut calculer le déterminant de la matrice, et c'est en quelque sorte le calcul de la matrice triangulaire.
Mais la solution est belle et claire, en plus de cela, il est facile de voir le critère selon lequel le système n'a pas de solutions.
Quelle est l'essence de la technique?
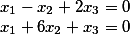
En résolvant ce système comme le produit de deux vecteurs, on obtient
i%20+%20(%201%20)j%20+%20(%207%20)k)
Par conséquent, les racines du système sont égales
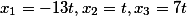
Pour ceux qui ne croient pas, cela se vérifie facilement par substitution.
Nous utilisons cette technique et examinons comment ces systèmes sont résolus à l'aide de produits vectoriels.
Nous avons donc le système source
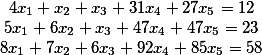
Déplacer les termes gratuits vers la gauche
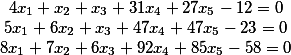
Nous avons eu 6 colonnes.
À ce stade, nous n'introduirons pas de nouvelles entités et n'utiliserons pas les concepts de rang matriciel dans notre travail. (Veuillez me traiter avec condescendance)
Nous voyons juste qu'il y a 3 équations et 5 variables. Par conséquent, la solution générale utilisera 5-3 = 2 variables indépendantes.
À la même étape, nous pouvons déterminer laquelle des variables sera libre. Nous prenons deux variables qui seront à droite de tous et les libérerons.
Remarque: Pour les autres équations, il ne s'avère pas toujours nécessaire de ne prendre que les derniers coefficients corrects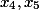
Et maintenant, en trois étapes, nous déterminons la solution fondamentale du système d'origine
Étape 1. Ici, la dernière colonne est les membres libres du système.
i%20+%20(%20-162%20)j%20+%20(%20-486%20)k%20+%20(%20-81%20)l)
Étape 2. Ici, la dernière colonne est les coefficients de la variable
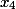
i%20+%20(%20162%20)j%20+%20(%20405%20)k%20+%20(%20-81%20)l)
Étape 3. Ici, la dernière colonne est les coefficients de la variable
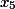
i%20+%20(%20243%20)j%20+%20(%20324%20)k%20+%20(%20-81%20)l)
Il n'est pas nécessaire de dire en détail d'où nous obtenons les données. Je pense que cela est évident pour les lecteurs. (Celui qui a résolu le système d'équations en utilisant la méthode Cramer trouvera des caractéristiques communes)
Ce qui est plus intéressant, c'est ce que nous ferons de ces «vecteurs».
Divisez-les par -81
nous obtenons les trois vecteurs suivants
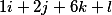
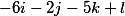
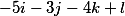
les disposer verticalement et donc la décision fondamentale prend la forme
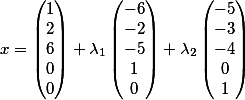
Super! N'est-ce pas ...
Pour le critère de solvabilité pour un système d'équations donné, dans la plupart des cas la règle de Kronecker-Copelli est utilisée, ici le résultat du produit vectoriel est simplement analysé.
Si le vecteur résultant a la forme
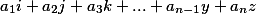
où 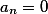 , et parmi tous les restants il y a au moins un non nul, alors un tel système de solutions n'a pasSi le vecteur résultant a tous les coefficients nuls, cela indique que l'une au moins des équations est une représentation linéaire de l'autre et / ou l'une des variables est proportionnelle à l'autre.
, et parmi tous les restants il y a au moins un non nul, alors un tel système de solutions n'a pasSi le vecteur résultant a tous les coefficients nuls, cela indique que l'une au moins des équations est une représentation linéaire de l'autre et / ou l'une des variables est proportionnelle à l'autre.Cet article est le premier, et j'aimerais entendre des commentaires, des critiques, des souhaits dans mon discours.
L'algorithme et la calculatrice ont été
créés en janvier 2019 et ce n'est qu'aujourd'hui que j'ai décidé de publier des informations sur Habré.
Si vous acceptez dans votre équipe / société, le sujet suivant sera
- Comment trouver une solution générale au système d'équations diophantiennes.