Visualiser des attracteurs étranges dans Plotly est un chef-d'œuvre

La poésie est une syllabe très belle, souvent réfléchie, que nous n'utilisons pas dans la vie de tous les jours, mais que nous aimons apprécier comme ça. On peut en dire autant des mathématiques. Dans le film "Pi", le protagoniste appelle les mathématiques "le langage de la nature", et dans le film "Games of the Mind", le protagoniste en parle comme d'une "forme d'art spéciale". Dans la vie de tous les jours, on peut l'oublier complètement.

L'apparition d'attracteurs étranges est inhabituelle et attrayante même dans la dimension bidimensionnelle. Plotly vous permet de les construire en trois dimensions, et il est très facile d'obtenir un modèle 3D que vous pouvez "tordre" et à travers lequel vous pouvez "voler" - un sens du "toucher".

Comment tout a commencé

Tout a commencé il y a longtemps, quelque part en 2007 à l'université, j'ai fait la connaissance de la théorie de l'auto-organisation et pour la première fois j'ai vu l'attracteur de Lorenz, son illustration en noir et blanc dans un livre. Ensuite, il m'a semblé trop étrange que quelque chose puisse se déplacer sur une trajectoire aussi inhabituelle. Encore plus étrange pour moi semblait l'idée même que presque tout dans le monde pouvait être décrit par une seule théorie.

En général, tout est comme d'habitude - ma vision du monde a changé, la vie a continué, le temps a passé. Et maintenant, plus récemment, je tombe sur un lien et vois ceci:


Image prise à partir de chaoticatmospheres.com

"Magnifique." J'ai pensé. L'idée que tout cela peut être construit dans Matplotlib a également clignoté, mais je savais déjà à l'avance que rien de spectaculaire ne fonctionnerait. Et récemment, il y a seulement deux semaines, j'ai rencontré Plotly et j'ai immédiatement réalisé que quelque chose pouvait en résulter.

La première tentative de construction a immédiatement échoué. Il s'est avéré que les formules de certaines images de la "Galerie des attracteurs étranges" contiennent des erreurs. Cependant, l'auteur de la galerie avertit honnêtement qu'il n'est pas un mathématicien, comme l'auteur de cet article.

Un court «google» a permis de retrouver ce code , qui s'est avéré extrêmement utile, et a été créé par Michael Tyka. Cette merveilleuse personne a fait un plug-in complet pour Blender, vous permettant de construire des modèles (!) De 60 attracteurs. En fait, ils peuvent être imprimés sur une imprimante 3D, et étant donné qu'il existe des technologies d'impression à la cire, il est assez facile d'obtenir un moule pour la coulée en bronze.

Code de visualisation

Eh bien, en plus d'être mathématicien amateur, je suis aussi programmeur amateur. Ne jugez donc pas strictement la qualité du code.

################################ ###   ### ################################ import numpy as np from scipy.integrate import odeint import plotly.graph_objects as go ################################## ###    ### ################################## #  : def LorenzMod1(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y*y - z*z + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.1 beta = 4 xi = 14 delta = 0.08 x_0, y_0, z_0 = 0, 1, 0 #      #  : tmax, n = 100, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod1, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) X, Y, Z = fT ####################### ###  ### ####################### # ,    : c = np.linspace(0, 1, n) #    : DATA = go.Scatter3d(x=X, y=Y, z=Z, line=dict(color= c, width=3, #   : # Greys,YlGnBu,Greens,YlOrRd,Bluered,RdBu, # Reds,Blues,Picnic,Rainbow,Portland,Jet, # Hot,Blackbody,Earth,Electric,Viridis,Cividis. colorscale="Cividis"), #   : mode='lines') fig = go.Figure(data=DATA) #   : fig.update_layout(width=1000, height=1000, margin=dict(r=10, l=10, b=10, t=10), #   : paper_bgcolor='rgb(0,0,0)', scene=dict(camera=dict(up=dict(x=0, y=0, z=1), eye=dict(x=0, y=1, z=1)), #   #     : aspectratio = dict(x=1, y=1, z=1), # ,    "aspectratio" aspectmode = 'manual', #  : xaxis=dict(visible=False), yaxis=dict(visible=False), zaxis=dict(visible=False) ) ) ###################### #!!  !!# ###################### fig.show() 

En conséquence, un modèle 3D d'un attracteur étrange appelé Lorenz Mod 1 devrait apparaître:


Il convient de noter tout de suite que pour résoudre des systèmes d'équations différentielles, la fonction odeint a été sélectionnée dans le module SciPy, ce qui m'a semblé le moyen le plus simple et le plus rapide pour créer du code de travail. Cependant, toutes les équations peuvent être résolues par la méthode Euler habituelle.

Pour indiquer les coefficients dans le code, par habitude, j'ai utilisé les noms des lettres grecques adoptées dans LaTeX. Lorsque vous travaillez avec des blocs-notes Jupyter, cela est parfois très utile, car les formules peuvent rapidement devenir du code et le code peut rapidement se transformer en formules.

Si vous êtes nouveau dans l'écosystème Python, mais que vous voulez garantir l'exécution du code, il est préférable d'installer la dernière version de la distribution Python Anaconda , et le package Plotly via conda est le gestionnaire de packages de distribution intégré.

Étant donné le nombre impressionnant d'attracteurs, il semble impossible de tous les construire. Par conséquent, dans cet article, je ne donnerai que les plus intéressants de ceux que j'ai réussi à construire.

L'attracteur Chen-Lee

 #  : def ChenLee(XYZ, t, alpha, beta, delta): x, y, z = XYZ x_dt = alpha*x - y*z y_dt = beta*y + x*z z_dt = delta*z + x*y/3 return x_dt, y_dt, z_dt #     : alpha = 5 beta = -10 delta = -0.38 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 200, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChenLee, (x_0, y_0, z_0), t, args=(alpha, beta, delta)) 

L'attracteur Chua

 #  : def ChuaAttractor(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ h = zeta*x + (0.5*(delta - zeta))*(np.abs(x + 1) - np.abs(x - 1)) x_dt = alpha*(-x + y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 15.6 beta = 25.58 zeta = -5/7 delta = -8/7 x_0, y_0, z_0 = 1.8, -0.7, -2.85 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

L'attracteur Coullet

 #  : def Coullet(XYZ, t, alpha, beta, zeta, delta): x, y, z = XYZ x_dt = y y_dt = z z_dt = alpha*x + beta*y + zeta*z + delta*x**3 return x_dt, y_dt, z_dt #     : alpha = 0.8 beta = -1.1 zeta = -0.4 delta = -1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 200, 20000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Coullet, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta)) 

L'attracteur Dadras

 #  : def DadrasAttractor(XYZ, t, rho, sigma, tau, zeta, epsilon): x, y, z = XYZ x_dt = y - rho*x + sigma*y*z y_dt = tau*y - x*z + z z_dt = zeta*x*y - epsilon*z return x_dt, y_dt, z_dt #     : rho = 3 sigma = 2.7 tau = 1.7 zeta = 2 epsilon = 9 x_0, y_0, z_0 = 0.1, 0.03, 0 #      #  : tmax, n = 220, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DadrasAttractor, (x_0, y_0, z_0), t, args=(rho, sigma, tau, zeta, epsilon)) 

L'attracteur Dequan Li

 #  : def DequanLi(XYZ, t, alpha, beta, delta, epsilon, rho, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = rho*x + xi*y -x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 1.833 delta = 0.16 epsilon = 0.65 rho = 55 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 50, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(DequanLi, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, rho, xi)) 

L'attracteur financier

 #  : def FinanceAttractor(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = (1/beta - alpha)*x + x*y + z y_dt = -beta*y - x**2 z_dt = -x - zeta*z return x_dt, y_dt, z_dt #     : alpha = 0.001 beta = 0.2 zeta = 1.1 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 300, 40000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FinanceAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

L'attracteur à quatre ailes

 #  : def FourWing(XYZ, t, alpha, beta, zeta): x, y, z = XYZ x_dt = alpha*x + y + y*z y_dt = -x*z + y*z z_dt = -z - zeta*x*y + beta return x_dt, y_dt, z_dt #     : alpha = 5 beta = 16 zeta = 2 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 60000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(FourWing, (x_0, y_0, z_0), t, args=(alpha, beta, zeta)) 

L'attracteur Hadley

 #  : def HadleyAttractor(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -y*y - z*z - alpha*x + alpha*xi y_dt = x*y - beta*x*z - y + delta z_dt = beta*x*y + x*zz return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 4 xi = 8 delta = 1 x_0, y_0, z_0 = 0.39, -1, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HadleyAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

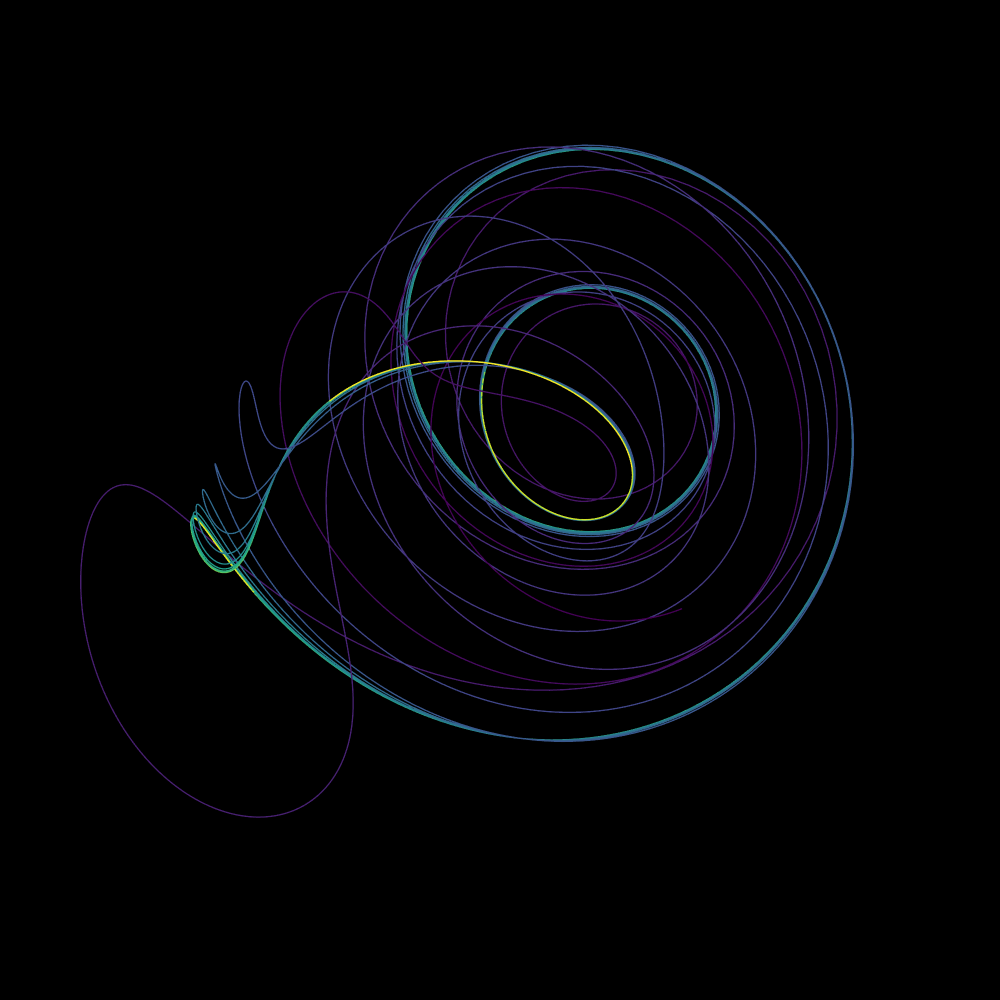
L'attracteur Halvorsen

 #  : def HalvorsenAttractor(XYZ, t, alpha): x, y, z = XYZ x_dt = -alpha*x - 4*y - 4*z - y*y y_dt = -alpha*y - 4*z - 4*x - z*z z_dt = -alpha*z - 4*x - 4*y - x*x return x_dt, y_dt, z_dt #     : alpha = 1.4 x_0, y_0, z_0 = -5, 0, 0 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(HalvorsenAttractor, (x_0, y_0, z_0), t, args=(alpha,)) 

L'attracteur Liu-Chen

 #  : def LiuChen(XYZ, t, alpha, beta, sigma, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*y + beta*x + sigma*y*z y_dt = delta*y - z + epsilon*x*z z_dt = xi*z - x*y return x_dt, y_dt, z_dt #     : alpha = 2.4 beta = -3.75 sigma = 14 delta = -11 epsilon = 4 xi = 5.58 x_0, y_0, z_0 = 1, 3, 5 #      #  : tmax, n = 55, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LiuChen, (x_0, y_0, z_0), t, args=(alpha, beta, sigma, delta, epsilon, xi)) 

L'attracteur Lorenz Mod 2

 #  : def LorenzMod2(XYZ, t, alpha, beta, xi, delta): x, y, z = XYZ x_dt = -alpha*x + y**2 -z**2 + alpha*xi y_dt = x*(y - beta*z) + delta z_dt = -z + x*(beta*y + z) return x_dt, y_dt, z_dt #     : alpha = 0.9 beta = 5 xi = 9.9 delta = 1 x_0, y_0, z_0 = 5, 5, 5 #      #  : tmax, n = 50, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(LorenzMod2, (x_0, y_0, z_0), t, args=(alpha, beta, xi, delta)) 

L'attracteur chaotique modifié de Chua

 #  : def ChuaModified(XYZ, t, alpha, beta, gamma, delta, zeta): x, y, z = XYZ h = -delta*np.sin((np.pi*x)/(2*gamma)) x_dt = alpha*(y - h) y_dt = x - y + z z_dt = -beta*y return x_dt, y_dt, z_dt #     : alpha = 10.82 beta = 14.286 gamma = 1.3 delta = 0.11 zeta = 7 x_0, y_0, z_0 = 1, 1, 0 #      #  : tmax, n = 200, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(ChuaModified, (x_0, y_0, z_0), t, args=(alpha, beta, gamma, delta, zeta)) 

L'attracteur Newton Leipnik

 #  : def NewtonLeipnik(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -alpha*x + y + 10*y*z y_dt = -x - 0.4*y + 5*x*z z_dt = beta*z - 5*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.175 x_0, y_0, z_0 = 0.349, 0, -0.16 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NewtonLeipnik, (x_0, y_0, z_0), t, args=(alpha, beta)) 

L'attracteur Nose-Hoover

 #  : def NoseHoover(XYZ, t, alpha): x, y, z = XYZ x_dt = y y_dt = -x + y*z z_dt = alpha - y*y return x_dt, y_dt, z_dt #     : alpha = 1.5 x_0, y_0, z_0 = 1, 0, 0 #      #  : tmax, n = 150, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(NoseHoover, (x_0, y_0, z_0), t, args=(alpha,)) 

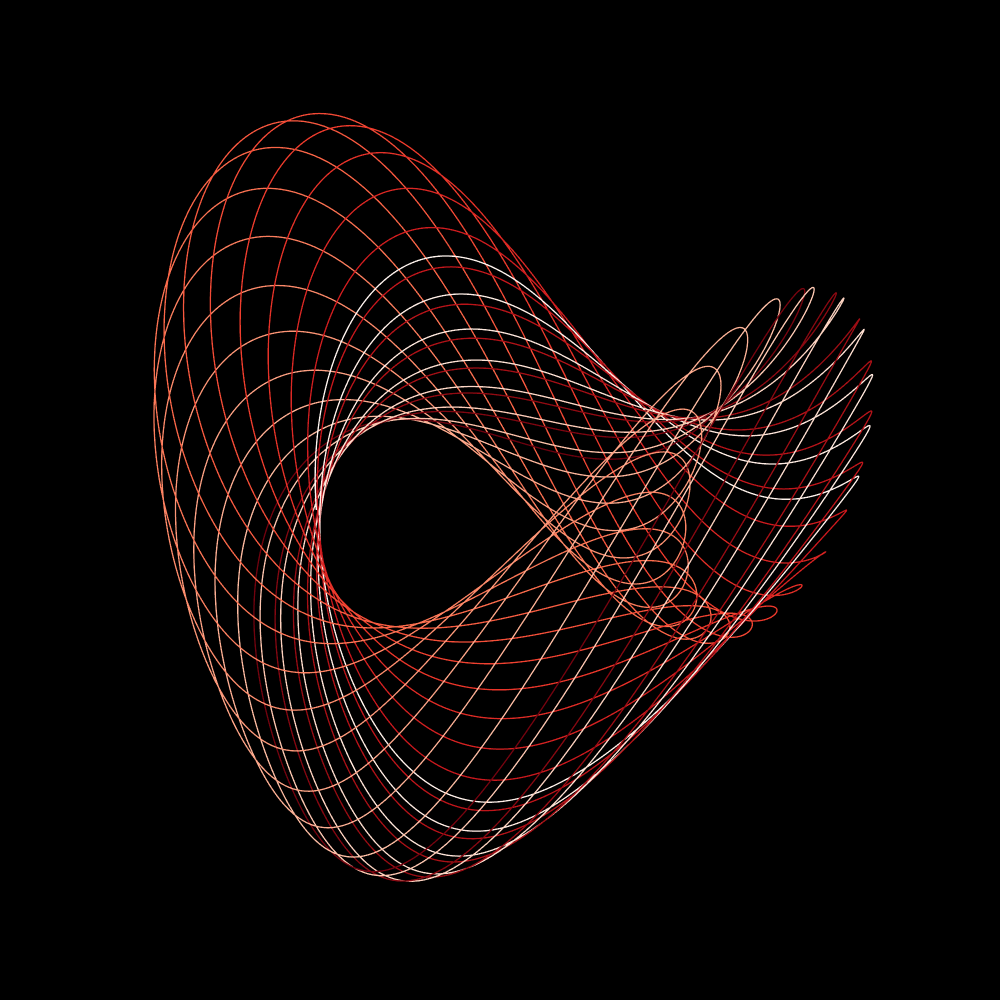
L'attracteur Roessler

 #  : def Roessler(XYZ, t, alpha, beta, sigma): x, y, z = XYZ x_dt = -(y + z) y_dt = x + alpha*y z_dt = beta + z*(x - sigma) return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = 0.2 sigma = 5.7 x_0, y_0, z_0 = 1, 1, 1 #      #  : tmax, n = 300, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Roessler, (x_0, y_0, z_0), t, args=(alpha, beta, sigma)) 

L'attracteur Sakarya

 #  : def SakaryaAttractor(XYZ, t, alpha, beta): x, y, z = XYZ x_dt = -x + y + y*z y_dt = -x - y + alpha*x*z z_dt = z - beta*x*y return x_dt, y_dt, z_dt #     : alpha = 0.4 beta = 0.3 x_0, y_0, z_0 = 1, -1, 1 #      #  : tmax, n = 100, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(SakaryaAttractor, (x_0, y_0, z_0), t, args=(alpha, beta)) 

L'attracteur Thomas

 #  : def Thomas(XYZ, t, beta): x, y, z = XYZ x_dt = -beta*x + np.sin(y) y_dt = -beta*y + np.sin(z) z_dt = -beta*z + np.sin(x) return x_dt, y_dt, z_dt #     : beta = 0.19 x_0, y_0, z_0 = 0.1, 0, 0 #      #  : tmax, n = 185, 10000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(Thomas, (x_0, y_0, z_0), t, args=(beta,)) 

L'attracteur de système chaotique unifié à trois rouleaux (TSUCS1)

 #  : def TSUCS1(XYZ, t, alpha, beta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*(y - x) + delta*x*z y_dt = xi*y - x*z z_dt = beta*z + x*y - epsilon*x*x return x_dt, y_dt, z_dt #     : alpha = 40 beta = 0.833 delta = 0.5 epsilon = 0.65 xi = 20 x_0, y_0, z_0 = 0.01, 0, 0 #      #  : tmax, n = 70, 50000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(TSUCS1, (x_0, y_0, z_0), t, args=(alpha, beta, delta, epsilon, xi)) 

L'attracteur wang-sun

 #  : def WangSunAttractor(XYZ, t, alpha, beta, zeta, delta, epsilon, xi): x, y, z = XYZ x_dt = alpha*x + zeta*y*z y_dt = beta*x + delta*y - x*z z_dt = epsilon*z + xi*x*y return x_dt, y_dt, z_dt #     : alpha = 0.2 beta = -0.01 zeta = 1 delta = -0.4 epsilon = -1 xi = -1 x_0, y_0, z_0 = 0.5, 0.1, 0.1 #      #  : tmax, n = 500, 30000 #       #   t: t = np.linspace(0, tmax, n) f = odeint(WangSunAttractor, (x_0, y_0, z_0), t, args=(alpha, beta, zeta, delta, epsilon, xi)) 

En conclusion

Feu, eau, terre, ciel, soleil, lune, étoiles - ce sont toutes les essences poétiques les plus anciennes. Très souvent, je parviens à trouver quelque chose d'aussi beau en mathématiques. Mais bien plus souvent, je ne comprends même pas comment parler de tout cela en langage mathématique et en langage ordinaire. Je ne comprends pas, mais je veux apprendre.

Mais ce que j'ai réalisé à 100%, c'est que les outils de visualisation modernes offrent une fantastique opportunité d'exprimer votre attitude par rapport à ce que vous faites maintenant, la possibilité de montrer à quel point cela est important pour vous et à quel point vous êtes intéressant. Faites tout sans mots.