J'ai écrit une fois un article dans lequel j'ai décrit un modèle mathématique simple de l'évolution d'un réseau neuronal et sa sélection pour la capacité d'ajouter des nombres dans des systèmes numériques avec des bases 2 et un nombre d'or, et il s'est avéré que le nombre d'or fonctionne mieux. Donc, ma première expérience s'est avérée très mauvaise, car je n'ai pas pris en compte un certain nombre de nuances importantes liées au fait que l'erreur ne doit pas être prise en compte pour un neurone, mais pour un peu d'information, j'ai donc décidé d'améliorer mon expérience, et d'en introduire quelques autres ajustements.

J'ai décidé de vérifier 100 paires d'échantillons de 15 (échantillon d'apprentissage) et 1000 (échantillon d'essai) dans des systèmes numériques avec des bases uniformément réparties de 1,2 à 2 au lieu de deux bases précédemment connues.
J'ai également fait une régression linéaire non seulement de la distance de la base au nombre d'or, mais aussi de la base elle-même, du nombre de coordonnées dans le vecteur et de la valeur moyenne des coordonnées dans le vecteur de réponse, pour prendre en compte la dépendance non linéaire de l'erreur sur la base.
J'ai également vérifié la normalité de certains échantillons selon le critère de Kolmogorov-Smirnov, ANOV, mais ces critères ont montré que les échantillons s'écartaient très probablement de la gaussienne, j'ai donc décidé de faire une régression linéaire pondérée au lieu de la régression habituelle. Cependant, l'ANOVA, bien qu'il ait montré un F un peu moins qu'auparavant (de l'ordre de 700-800 au lieu de 800-900), mais le résultat est resté plus que statistiquement significatif, ce qui signifie que plus de tests devraient être effectués. Au cours de ces tests, j'ai pris un histogramme de la densité de distribution des résidus de régression et du QQ normal - un graphique de la fonction de distribution de ces résidus.

Ces deux graphiques sont:

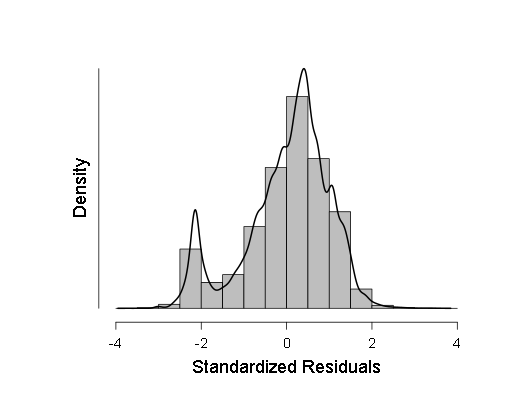
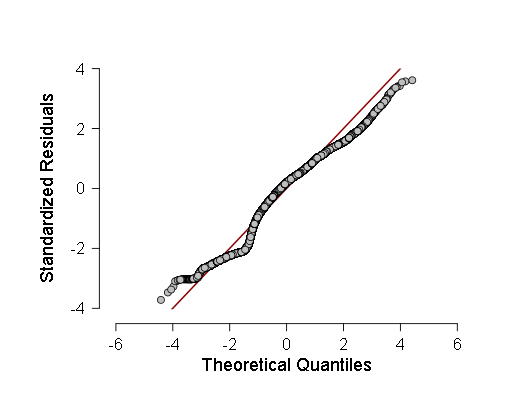
Comme on peut le voir, bien que l'écart par rapport à la distribution normale dans la distribution des résidus soit statistiquement significatif (et à gauche, même un petit deuxième mode est visible sur l'histogramme), en fait il est très proche du gaussien, donc, il est possible (avec prudence et des intervalles de confiance plus grands) de s'appuyer sur cette régression linéaire .

Maintenant, comment j'ai généré des échantillons pour tester les réseaux de neurones sur eux.

Voici le code pour générer les échantillons:

#define _CRT_RAND_S //     rand_s() #include "main.h" //   (    ) int main(void) { FILE *output,*test; int i; while (fopen("test.txt","w")==NULL) i=0; output=fopen("test.txt","w"); //       unsigned int p; p=0;//       rand_s(); rand_s(&p); double a; a=0; a = 1.6+((double) ((double) ((double)p/UINT_MAX)-0.5)*0.8);//    int n; n=0;//     . bool *t;//         . while (malloc(sizeof(bool)*1000)==NULL) n=0; t = (bool *) malloc(sizeof(bool)*1000); rand_s(&p); double s; s=0; s = (double)p/UINT_MAX;//    0  1. calculus(a,s,t,1000);// s  a-  . double mu; int q; mu=0; q=0; for (i=0;i<1000;i++) { if ((*(t+i))==true) mu =(double) mu+1; }//     , . . ,     . mu=(double) mu/1000; printf("%10.9lf\n",mu); n = (int) ((double) 14)/(log(mu)*mu/(log((double) 1/2))+log((double) 1-mu)*(1-mu)/log((double) 1/2)); //   ,     14    a-  . printf("%i\n",n); free(t); while (malloc(sizeof(bool)*n)==NULL) i=0; t = (bool *) malloc(n*sizeof(bool));//     ,      . double x,y,z; x=0; y=0; z=0; int j; j=0; int m; m=0; m=2*n; fprintf(output,"%i 1000\n",m);//         -. fprintf(output,"%lf\n",a); //    for (i=0;i<1000;i++) {//     ,  ,     ,   -  . rand_s(&p); x = (double) p/UINT_MAX; rand_s(&p); y = (double) p/UINT_MAX; z=x+y; calculus(a,x,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(output,"1 "); else fprintf(output,"0 "); } calculus(a,y,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(output,"1 "); else fprintf(output,"0 "); } fprintf(output,"\n"); calculus(a,z,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(output,"1 "); else fprintf(output,"0 "); } for (j=0;j<n;j++) { fprintf(output,"0 "); } fprintf(output,"\n"); } //    ,     ,    15  . while (fopen("input.txt","w")==NULL) i=0; test = fopen("input.txt","w"); fprintf(test,"%i 15\n",m); fprintf(test,"%lf\n",a); for (i=0;i<15;i++) { rand_s(&p); x = (double) p/UINT_MAX; rand_s(&p); y = (double) p/UINT_MAX; z=x+y; calculus(a,x,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(test,"1 "); else fprintf(test,"0 "); } calculus(a,y,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(test,"1 "); else fprintf(test,"0 "); } fprintf(test,"\n"); calculus(a,z,t,n); for (j=0;j<n;j++) { if ((*(t+j))==true) fprintf(test,"1 "); else fprintf(test,"0 "); } for (j=0;j<n;j++){ fprintf(test,"0 "); } fprintf(test,"\n"); } free(t); fclose(output); fclose(test); };

Et voici le code du fichier d'en-tête:

 #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);//     x   a   t  n . void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; //  t   . for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;//    ,   . while ((l<=k-1)&&(m<nk-1)) //  x  a ( ),      { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=yb; (*(t+kl))=true; } } else { b=1; m=0; while ((b>y)&&(m<nk-1)) { b=b/a; m++; } if ((b<y)||(m<nk-1)) { y=yb; (*(t+k+m))=true; } } } return; }

J'ai également décidé de publier le code complet du réseau neuronal:

 #include "main.h" //    ,   ,       main(void). int main(void) { FILE *input, *output, *test; int i,j,k,k1,k2,l,q,n,m,r; double *x,*y,*z,*a,s,s1,h,h1,d,mu,buffer; d=0; mu=0; r=0; unsigned int p; n=0; while (fopen("input.txt","r")==NULL) i=0; while (fopen("output.txt","w")==NULL) i=0; input = fopen("input.txt","r"); output = fopen("output.txt","w"); fscanf(input,"%i %i",&n,&m);//      . buffer=0; fscanf(input,"%lf",&buffer);//        . while (malloc(sizeof(double)*n*m)==NULL) i=0; x = (double *) malloc(sizeof(double)*n*m);//     while (malloc(sizeof(double)*n*m)==NULL) i=0; z = (double *) malloc(sizeof(double)*n*m);//       . while (malloc(sizeof(double)*n*m)==NULL) i=0; y = (double *) malloc(sizeof(double)*n*m);//    . for (k=0;k<m;k++) { for (i=0;i<n;i++) { fscanf(input,"%lf ",x+n*k+i);// . } for (i=0;i<n;i++) { fscanf(input,"%lf ",y+n*k+i);// . } for (i=0;i<n;i++) { (*(z+n*k+i))=0;//       . } } while (malloc(sizeof(double)*n*n)==NULL) i=0; a = (double *) malloc(sizeof(double)*n*n); //    . for (i=0;i<n*n;i++) { (*(a+i))=0; } k1 = 0; k2 = 0; s=1; s1=0; s1=s+1; d=0; h=0; q=0; mu=1; while (((d-mu)*(d-mu)>0.01)||(q<10))// ,           ,     ,     -  . { s=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } for (i=0;i<n;i++) { for (j=0;j<n;j++) { (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j));//     . } } for (i=0;i<n;i++) { s=s+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i)));//         } } r=0; s1=s+1; while ((s<s1)&&(r<100))//,                     . { r++; s1=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } //      rand_s(&p); k1 = (int) (p/((int) (UINT_MAX/n))); rand_s(&p); k2 = (int) (p/((int) (UINT_MAX/n))); rand_s(&p); //   h=((double) p/UINT_MAX)-0.5; h1=1; rand_s(&p); l=((int) ((double) p/UINT_MAX)*20); // ,           . for (i=0;i<l;i++) { h1=h1/10; } h=h*h1; //      . for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { if ((i==k1)&&(j==k2)) (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j))+h*(*(x+k*n+j)); else (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } //        . for (i=0;i<n;i++) { s1=s1+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i))); } } } if (r<100) (*(a+k1*n+k2))=(*(a+k1*n+k2))+h; s1=0; d=0; for (k1=0;k1<n;k1++) { for (k2=0;k2<n;k2++) { for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { if ((i==k1)&&(j==k2)) (*(z+k*n+i))=(*(z+k*n+i))+((*(a+i*n+j))+0.1)*(*(x+k*n+j)); else (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } } s1=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { s1=s1+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i))); } } d=d+(s1-s)*(s1-s)/(n*m); } } mu=mu*((double) q/(q+1))+((double) d/(q+1)); q=q+1; printf("%lf \n",mu); } for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } //       . for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } } free(x); free(y); free(z); while (fopen("test.txt","r")==NULL) i=0; test = fopen("test.txt","r"); fscanf(test,"%i %i",&n,&m); fscanf(test,"%lf",&buffer); while (malloc(n*m*sizeof(double))==NULL) i=0; x = (double *) malloc(n*m*sizeof(double)); while (malloc(n*m*sizeof(double))==NULL) i=0; y = (double *) malloc(n*m*sizeof(double)); while (malloc(n*m*sizeof(double))==NULL) i=0; z = (double *) malloc(n*m*sizeof(double)); for (k=0;k<m;k++) { for (i=0;i<n;i++) { (*(z+k*n+i))=0; } } for (k=0;k<m;k++) { for (i=0;i<n;i++) { fscanf(test,"%lf ",x+k*n+i); } for (i=0;i<n;i++) { fscanf(test,"%lf ",y+k*n+i); } } //      (  ). mu=0; for (k=0;k<m;k++) { for (i=0;i<n;i++) { mu=mu+(*(y+k*n+i)); } } mu=mu/((double) k*n); fprintf(output,"%lf\n\n",mu); for (k=0;k<m;k++) { for (i=0;i<n;i++) { for (j=0;j<n;j++) { (*(z+k*n+i))=(*(z+k*n+i))+(*(a+i*n+j))*(*(x+k*n+j)); } } } //     . for (k=0;k<m;k++) { s=0; for (i=0;i<n;i++) { s=s+((*(z+k*n+i))-(*(y+k*n+i)))*((*(z+k*n+i))-(*(y+k*n+i))); } s=(double) s/n; s=sqrt(s); s=(double) ((double) s*n)/14; fprintf(output,"%20.18lf \n",s); } free(a); free(x); free(y); free(z); fclose(input); fclose(output); return 0; };

Ensuite, parlons de la façon dont j'ai effectué une régression linéaire pondérée. Pour ce faire, j'ai simplement calculé les écarts-types des résultats du réseau neuronal, puis divisé l'unité en eux.

Voici le code source du programme avec lequel j'ai fait cela:

 #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");//         . double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; };

Ensuite, j'ai ajouté les poids résultants au tableau, où j'ai réduit toutes les données obtenues à la suite du programme, ainsi que les valeurs des variables pour calculer la régression, puis les ai calculées dans JASP. Voici les résultats:

Résultats

Régression linéaire

Résumé du modèle
Modèle	R	R²	R² ajusté	Rmse
1	0,175	0,031	0,031	0,396

Anova
Modèle		Somme des carrés	df	Carré moyen	F	p
1	Régression	494,334	4	123,584	789.273	<.001
	Résiduel	15657.122	99995	0,157
	Total	16151.457	99999

Coefficients
Modèle		Non standardisé	Erreur standard	Standardisé	t	p	0,5%	99,5%
1	(Intercepter)	-0,104	0,059		-1,751	0,080	-0,256	0,049
	La distance entre la base et le nombre d'or	-0.113	0,010	-0,080	-11,731	<.001	-0,138	-0,088
	Le nombre de mesures dans le vecteur	0,008	2,328e -4	0,529	32,568	<.001	0,007	0,008
	La valeur moyenne de la coordonnée vectorielle dans la réponse	-0,951	0,181	-0,332	-5,255	<.001	-1,417	-0,485
	Système de numérotation de base	0,489	0,048	0,687	10.252	<.001	0,366	0,611

Ensuite, j'ai un histogramme de la densité de distribution des résidus de régression standardisés:

Ainsi que le graphique quantile-quantile normal des résidus de régression normalisés:

J'ai ensuite appliqué les valeurs moyennes des coefficients de régression obtenus au cours de son parcours aux variables, et effectué mon analyse statistique pour trouver le minimum le plus probable de la fonction d'erreur à partir de la base du système numérique (combien elle est liée à ces variables) en utilisant le lemme de Fermat, le théorème de Bayes et le théorème de Lagrange comme suit:
Le fait est que la distribution des bases du système numérique dans l'échantillon était évidemment uniforme, donc si une certaine base dans l'intervalle (1,2; 2) est le minimum de l'erreur quadratique moyenne, alors, selon le lemme de Fermat, elle aura une dérivée nulle, puis la densité de probabilité des valeurs La fonction sera infinie.
Maintenant, comment j'ai appliqué le théorème de Bayes. J'ai calculé les intervalles de confiance de la distribution bêta (c'est la distribution de probabilité de «succès» dans l'expérience sous la condition de n «succès» et m «échecs» avec densité de probabilité

p (x) = f r a c (n + m + 1)! n! m! x^{n} (1 - x)^{m}

$p (x) = \ frac {(n + m + 1)!} {n! m!} {x ^ n} {(1-x) ^ m}$ ) les valeurs de la fonction de distribution (c'est la probabilité que la variable aléatoire ne soit pas plus grande que l'argument) des erreurs calculées, basées sur le fait que si la variable aléatoire n'est pas plus grande que l'argument, c'est «succès», et si elle est plus, alors «échec». Ensuite, en utilisant le théorème bayésien, nous appliquons la distribution bêta de la fonction de distribution des erreurs calculées et calculons ses intervalles de confiance [fonction de distribution] de 99% dans chaque erreur calculée.
Nous passons au théorème de Lagrange. Le théorème de Lagrange déclare que si la fonction f (x) est continuellement différenciable sur l'intervalle [a; b], alors au moins à un point de cet intervalle elle a une dérivée égale à

f r a c f (b) - f (a) b - a

$\ frac {f (b) -f (a)} {b-a}$ . Comment j'applique ce théorème: le fait est que la densité de probabilité est une dérivée de la fonction de distribution, donc je prends la valeur maximale parmi celles qu'elle prend exactement à certains intervalles de l'erreur minimale aux erreurs restantes. Ensuite, je calcule les intervalles de confiance de ces valeurs à 98% (en utilisant la correction de Bonferroni) en utilisant la formule suivante:

[f r a c F_{1} (x_{i}) - F_{2} (x_{1}) x_{i} - x_{1}; f r a c F_{2} (x_{i}) - F_{1} (x_{1}) x_{i} - x_{1}]

$[\ frac {F_1 (x_i) -F_2 (x_1)} {x_i-x_1}; \ frac {F_2 (x_i) -F_1 (x_1)} {x_i-x_1}]$

où F1 est l'extrémité gauche de l'intervalle de confiance pour la fonction de distribution et F2 est la droite, x_i, x_1 sont les erreurs calculées comme argument de la fonction de distribution. Ensuite, le programme recherche un intervalle avec la plus grande extrémité gauche et la plus grande extrémité droite (de sorte que la valeur de l'intervalle soit maximale), puis recherche le maximum et le minimum dans les bases qui correspondent aux erreurs calculées dans cet intervalle. Ces maximum et minimum sont les arguments de la fonction d'erreur à partir du bas, entre lesquels se situe le minimum de la fonction elle-même avec une probabilité de 98%.

Voici le code du programme que j'ai effectué cette analyse statistique avec explications:

 #include "main.h" //  . int main(void) { FILE *input,*output; int i,n,k,dFmax; double *x,*y,*F1,*F2,*F,*dF,*dF1,*dF2,t1,t2,xmin,xmax,ymin,ymax; t1=0; t2=0; while ((input=fopen("input.txt","r"))==NULL) i=0; while ((output=fopen("output.txt","w"))==NULL) i=0; n=0; while (fscanf(input,"%i",&n)==NULL) i=0; while ((x = (double *) malloc(sizeof(double)*n))==NULL) //    . i=0; while ((y = (double *) malloc(sizeof(double)*n))==NULL) //  ,   . i=0; while ((F = (double *) malloc(sizeof(double)*n))==NULL) //   -   . i=0; while ((F1 = (double *) malloc(sizeof(double)*n))==NULL) //      -. i=0; while ((F2 = (double *) malloc(sizeof(double)*n))==NULL)//      -. i=0; for (i=0;i<n;i++) { while (fscanf(input,"%lf %lf",y+i,x+i)==NULL) k=0; } for (i=0;i<n;i++) { Bayesian_99CI(i,ni,*(F1+i),*(F2+i),*(F+i)); //     ,     (     ) printf("%lf %lf %lf\n",*(F+i),*(F1+i),*(F2+i)); } while ((dF = (double *) malloc(sizeof(double)*n))==NULL) i=0; while ((dF1 = (double *) malloc(sizeof(double)*n))==NULL) i=0; while ((dF2 = (double *) malloc(sizeof(double)*n))==NULL) i=0; for (i=0;i<n-1;i++) //  " -"     . { for (k=i+1;k<n;k++) { if ((*(y+k))<(*(y+i))) { t1=(*(x+i)); t2=(*(y+i)); (*(x+i))=(*(x+k)); (*(y+i))=(*(y+k)); (*(x+k))=t1; (*(y+k))=t2; } } } dFmax=1; //     98%   ,       1-  (i+1)-        : for (i=1;i<n;i++) { (*(dF2+i))=((*(F2+i))-(*(F1)))/((*(y+i))-(*(y))); (*(dF1+i))=((*(F1+i))-(*(F2)))/((*(y+i))-(*(y))); } for (i=1;i<n;i++) { if (((*(dF1+i))>(*(dF1+dFmax)))&&((*(dF2+i))>(*(dF2+dFmax)))) dFmax=i; } xmin=0; xmax=0; ymin=0; ymax=0; xmin=(*x); xmax=(*x); ymin=(*y); ymax=(*y); //  ,       ,    ,      : for (i=0;i<=dFmax;i++) { if ((*(x+i))>xmax) xmax=(*(x+i)); if ((*(x+i))<xmin) xmin=(*(x+i)); if ((*(y+i))>ymax) ymax=(*(y+i)); if ((*(y+i))<ymin) ymin=(*(y+i)); }     : fprintf(output,"x (- [%lf; %lf]\ny (- [%lf; %lf]",xmin,xmax,ymin,ymax); scanf("%i\n",&i); free(x); free(y); free(F); free(F1); free(F2); free(dF); free(dF1); free(dF2); fclose(input); fclose(output); return 0; };

Et voici le code du fichier d'en-tête:

 #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);//   -  n ""  m "",     "    "  "   " ,     : double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);//   - (      ): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,mi,x); } c = (double) c/(n+m+2); return c; } //        : void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }

Voici le résultat du travail de ce programme, quand je lui ai donné les fondements du système numérique et les résultats de la régression:

 x (- [1.501815; 1.663988] y (- [0.815782; 0.816937]

("(-" dans ce cas n'est qu'une notation du signe "appartient" de la théorie des ensembles, et les crochets indiquent l'intervalle.)

Ainsi, il s'est avéré que la meilleure base du système de numérotation en termes de nombre minimal d'erreurs dans la transmission d'informations se situe dans la plage de 1,501815 à 1,663988, c'est-à-dire que le nombre d'or y tombe complètement. Certes, j'ai fait une hypothèse lors du calcul du minimum et une autre lors du calcul de la quantité d'informations dans différents systèmes numériques: premièrement, j'ai supposé que la fonction d'erreur de la base est continuellement différenciable, et deuxièmement, que la probabilité que le nombre uniformément distribué soit de 1, 2 à 2 auront le numéro un dans un chiffre spécifique, il sera approximativement le même après un chiffre après la virgule décimale.

Si j'ai fait quelque chose de complètement faux, ou simplement de mal, je suis ouvert aux critiques et aux suggestions. J'espère que cette tentative a été plus réussie.
UPD J'ai édité l'article deux fois pour clarifier certains endroits de la partie «purement scientifique», et j'ai également formaté le code.
UPD2. Après avoir consulté une personne qui comprend la bioinformatique (diplômée de l'étude de troisième cycle FBB MSU à l'IPPI RAS), il a été décidé de remplacer le mot 《cerveau》 par 《réseau de neurones》, car ils diffèrent considérablement.

Réseaux de neurones et nombre d'or: deuxième série

Résultats

Régression linéaire

More articles: