Il est peut-être difficile d'appeler les dômes géodésiques quelque chose d'inhabituel ou de nouveau. Dans cet article, je vais parler un peu de ces conceptions en général, de leur structure, et montrer également, à titre d'exemple, comment j'ai envisagé quelque chose sur ce sujet. Le code sera également.
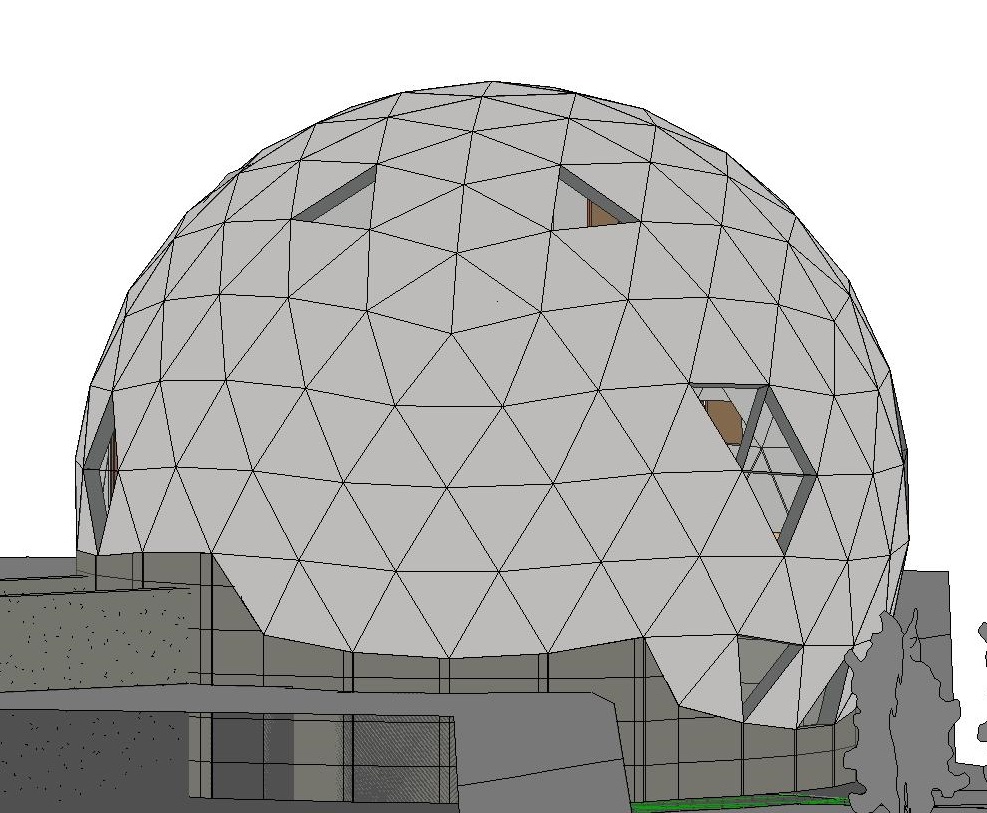
Je ne citerai pas Wikipédia. Pourquoi ai-je choisi le dôme comme maison?
- A volume égal, la surface de la sphère sera inférieure à celle de toute autre forme. Cela affecte positivement la consommation de matériaux et la consommation d'énergie pendant le fonctionnement.
- J'aime à quoi ressemble la sphère.
- Il s'agit d'un projet d'ingénierie intéressant, en un sens, voire d'un défi. C'est difficile, difficile et donc amusant!
Comment ces sphères géodésiques sont-elles disposées en général? À première vue, il semble qu'il s'agisse d'une sorte d'imbrication des bords et qu'il est difficile d'attraper le système. Nous allons essayer de comprendre cela.
La base de telles structures est l'icosaèdre ou l'octaèdre. En général, un polyèdre régulier.
Dans mon cas, c'était précisément l'icosaèdre et il est utilisé plus souvent. Ensuite, nous prenons une face et la remplaçons par plusieurs triangles dont les sommets se trouvent sur une sphère dont le centre coïncide avec le centre de l'icosaèdre. Cela ne semble pas trop bon. Faisons une digression.
Il y a une merveilleuse calculatrice
www.acidome.ru qui vous permet de tordre un géomètre en temps réel. Prenez l'icosaèdre comme base, réglez la fréquence sur 1, partie de la sphère 1/1.

Ceci est notre principal icosaèdre. La fréquence est le nombre de pièces que nous briserons chaque bord de l'icosaèdre. Nous fixons 3,4, 5 et rien ne devient clair. Passez en mode toit et recherchez les pentagones. Dans les endroits où nous avons le sommet de l'icosaèdre - il y aura un pentagone. Entre les trois pentagones se trouve la face de l'icosaèdre.

Si vous regardez attentivement la géodésique et savez quoi chercher (généralement un pentagone), alors la régularité de la structure devient visible. Sur la biosphère de Montréal, avec une diligence raisonnable, vous pouvez trouver des pentagones et calculer la fréquence. Notre fréquence est égale au nombre d'arêtes entre deux pentagones.
Les «grands» triangles eux-mêmes, avec des sommets au sommet de l'icosaèdre, ont également une structure. Sur les toitures à l'acidome, cela est visible en couleur. Les triangles sont situés symétriquement par rapport au centre du "grand" triangle. Le nombre de leurs types est inférieur au nombre total de triangles. Dans le cas d'une fréquence de 5 triangles uniques 9.

Dans le processus de conception d'une maison, j'ai été confronté à la tâche de construire une sphère dans Dynamo. Il s'agit d'un outil qui vous permet d'apprendre à Autodesk Revit à travailler avec des formulaires complexes. Un tel environnement de programmation visuelle.
Googler, j'ai même trouvé une esquisse qui a construit une sphère géodésique dans Dynamo. Il a construit la sphère, mais pas celle-là.
Voici le truc. Lorsque nous prenons un bord de l'icosaèdre et le divisons en petits triangles - cela peut se faire de plusieurs manières. Dans l'acidome, le commutateur «méthode de fractionnement» en est responsable.
L'esquisse trouvée a construit la sphère en utilisant la méthode des accords égaux. Qu'est-ce que cela signifie? Nous prenons un grand triangle de l'icosaèdre, divisons chacune de ses arêtes en le nombre de pièces dont nous avons besoin, connectons les points sur les arêtes entre elles et obtenons une grille plate de triangles. Ensuite, nous projetons cette grille sur la sphère. Tout irait bien, mais ces triangles eux-mêmes sont de tailles assez différentes. Central surtout. C'est compréhensible, le centre du «grand» triangle est à notre distance maximale de la sphère. C'est mauvais, car dans ce cas, il est plus difficile d'optimiser la consommation de matériaux. Il y aura plus de gaspillage.
Une autre méthode de division (avec des arcs égaux) suppose que nous construisons au-dessus du «grand» triangle de l'arc et les divisons déjà en parties égales. L'approche est différente, une simple projection ne peut pas faire.
Le croquis ne correspondait pas. J'ai essayé de le réparer et à la fin j'ai dû me plonger dans cette affaire avec ma tête.
Il s'est avéré qu'en plus de l'environnement visuel, Dynamo a intégré Python. Je n'ai jamais rencontré cette langue auparavant, mais où notre langue n'a-t-elle pas disparu? Au final, ce n'est qu'un outil.
Ensuite, il y aura des morceaux de code, faites attention que c'est mon monde bonjour en python, et le but n'était pas de construire la solution la plus efficace et la plus efficace, mais de construire la bonne sphère.
La méthode des arcs égaux.
Nous prenons l'une des faces de l'icosaèdre et construisons des arcs à partir des coins de ce triangle.
for k, edge in enumerate(curves):

Ensuite, nous divisons les arcs en parties égales et connectons les points sur les arcs avec de nouveaux arcs. Tous les arcs ont un centre - le centre de la sphère. Les points ne sont pas tous connectés avec tous, mais du même nom. Dans l'image, cela semble plus simple que dans le code.
for edge_index, point_list in enumerate(points): edge_arcs = [] for point_index, point in enumerate(point_list): next_edge_index = edge_index + 1 if len(points) == next_edge_index: next_edge_index = 0 end_point_index = n - point_index - 2 arc = Arc.ByCenterPointStartPointEndPoint(center_point, points[next_edge_index][end_point_index], point) if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, point, points[next_edge_index][end_point_index]) arc_points_count = n - point_index - 1; pp = Arc.PointsAtEqualSegmentLength(arc, arc_points_count) for po in pp: on_arc_points.append(po) edge_arcs.append(arc) edges_arcs.append(edge_arcs)

Oups, et les arcs ne se coupent pas! Le googling pas trop fluide m'a amené à un livre qui a confirmé mes hypothèses qu'il est nécessaire d'utiliser le centre d'un triangle formé par l'intersection d'arcs comme le haut du bord de la géodésique. J'ai également fumé les sources d'acidome, mais je ne me souviens pas si j'y ai trouvé une confirmation. Je me souviens que c'était intéressant.
Il faut en quelque sorte trouver les centres. C'est le centre du triangle et ce n'est pas difficile, mais il fallait comprendre où se trouvent ces triangles dans le tas de points. Cela me semblait l'option la plus simple pour connecter les points les plus proches les uns des autres.
for point in on_arc_points: distance = []

Nous devons maintenant interconnecter les points collectés à différentes étapes, qui sont les sommets des bords de la sphère géodésique. Dans l'image, ces points sont clairement visibles, mais lorsqu'ils sont dans le tableau - tout est plus compliqué. Il y avait plusieurs options, mais comme la tâche consistait à obtenir un script de travail avec le moins d'effort, cela est sorti:
Le segment est prêt. Il existe probablement une bonne façon de résoudre ce problème, mais j'ai ouvert la mienne.

Ensuite, le segment se déplie, il est copié plusieurs fois, copié et une sphère complète est obtenue. Voici l'un des rebondissements:
v = Vector.ByTwoPoints(sphere_center, curves[0].StartPoint) for face_triangle in face_triangles: geodesic_sphere.append(Geometry.Rotate(face_triangle, sphere_center, v, 72))
Le script est sorti moche, je l'ai copié plusieurs fois, car il y avait des problèmes avec l'exportation vers Revit. Je pensais qu'il y avait des problèmes avec la construction. Du coup, sur le forum Dynamo, l'Indien a incité l'Ukrainien et tout a réussi!
Vous pouvez maintenant créer une sphère de toute fréquence et de tout diamètre. Une comparaison des tailles avec les résultats de l'acidome a montré que tout converge avec une grande précision. La répétabilité est bonne.

J'ai également commencé à optimiser les tailles pour minimiser la récolte. Puisque toutes les tailles étaient entre mes mains, ce n'était pas si difficile. En conséquence, le rayon de la sphère s'est avéré être de 5,65 mètres à une fréquence de 5. De telles dimensions me permettent d'utiliser les matériaux de 125 cm de large assez efficacement. Ces largeurs sont des feuilles de OSB, de la tôle, de l'isolation, des cloisons sèches. Avec une bonne optimisation, le nombre de coupures est minime. Les meilleurs résultats peuvent être obtenus en calculant la disposition des triangles sur le matériau, mais je ne l'ai pas fait.
De plus, c'était plus facile, car Revit mangeait une forme complexe et permettait de travailler avec elle avec à peu près le même succès qu'avec le carré-parallèle.
Bien sûr, les difficultés ne se sont pas arrêtées là, mais c'est une histoire complètement différente.