Nous écrivons une «calculatrice» en C #. Partie I. Calcul de la valeur, dérivé, simplification et autres oies

Salut

Pour une raison quelconque, notre calculatrice est associée à quelque chose que chaque débutant devrait écrire. Peut-être parce que les ordinateurs ont été créés à cet effet pour compter. Mais nous écrirons une calculatrice difficile, pas sympa bien sûr, mais pour pouvoir faire des opérations algébriques de base, comme la différenciation, la simplification, et des fonctionnalités comme la compilation pour accélérer les calculs.


Nous prenons les cookies restants de la nouvelle année, et avons roulé!

Assemblage d'expression

Qu'est-ce qu'une expression?

Bien sûr, ce n'est pas une ligne. Il est assez évident qu'une formule mathématique est soit un arbre, soit une pile, et ici nous nous arrêtons au premier. Autrement dit, chaque nœud, chaque nœud de cet arbre, est une sorte d'opération, variable ou constante.



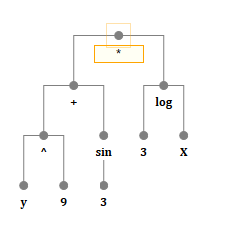
Une opération est soit une fonction, soit un opérateur, en principe, à peu près la même chose. Ses enfants sont les arguments d'une fonction (opérateur).

Hiérarchie des classes dans votre code

Bien sûr, l'implémentation peut être quelconque. Cependant, l'idée est que si votre arbre se compose uniquement de nœuds et de feuilles, ils sont différents. Par conséquent, j'appelle ces «choses» - des entités. Par conséquent, la classe supérieure sera l'entité de classe abstraite.


Et il y aura également quatre classes successives: NumberEntity, VariableEntity, OperatorEntity, FunctionEntity.

Comment construire une expression?

Tout d'abord, nous allons construire une expression dans le code, c'est-à-dire

var x = new VariableEntity("x"); var expr = x * x + 3 * x + 12; 

Si vous déclarez une classe VariableEntity vide, un tel code vous générera une erreur, disent-ils, ne sait pas comment multiplier et additionner.

Remplacer les opérateurs

Une fonctionnalité très importante et utile de la plupart des langues, vous permettant de personnaliser l'exécution des opérations arithmétiques. Il est implémenté syntaxiquement différemment selon la langue. Par exemple, une implémentation en C #

 public static YourClass operator +(YourClass a, YourClass b) { return new YourClass(a.ToString() + b.ToString()); } 

En savoir plus sur la substitution des instructions en C #
Le navet est implémenté ici .

Casting (non) explicite

Dans les langages compilés tels que C #, une telle chose est généralement présente et vous permet de transtyper le type si nécessaire sans appeler en plus myvar.ToAnotherType (). Ainsi, par exemple, il serait pratique d'écrire

 NumberEntity myvar = 3; 

Au lieu de l'habituel

 NumberEntity myvar = new NumberEntity(3); 

En savoir plus sur la coulée de caractères en C #
Le navet est mis en place sur cette ligne.

Accrocher

La classe Entity a un champ Enfants - ce n'est qu'une liste d'entités, qui sont les arguments de cette entité.


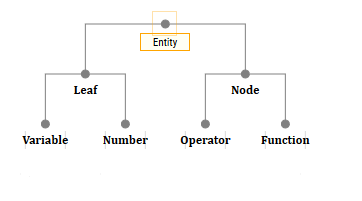
Lorsque nous appelons une fonction ou un opérateur, nous devons créer une nouvelle entité et y mettre les enfants à partir desquels la fonction ou l'opérateur est appelé. Par exemple, le montant en théorie devrait ressembler à ceci:

 public static Entity operator +(Entity a, Entity b){ var res = new OperatorEntity("+"); res.Children.Add(a); res.Children.Add(b); return res; } 

Autrement dit, si nous avons l'entité x et l'entité 3, alors x + 3 renverra l'essence de l'opérateur de somme avec deux enfants: 3 et x. Ainsi, nous pouvons construire des arbres d'expression.

Un appel de fonction est plus simple et pas aussi beau qu'avec un opérateur:

 public Entity Sin(Entity a) { var res = new FunctionEntity("sin"); res.Children.Add(a); return res; } 

La pendaison de navets est implémentée ici .

Ok, nous avons créé un arbre d'expression.

Substitution variable

Ici, tout est extrêmement simple. Nous avons Entity - nous vérifions s'il s'agit d'une variable elle-même, si c'est le cas, nous renvoyons la valeur, sinon nous parcourons les enfants.

Cet énorme fichier de 48 lignes implémente une fonction aussi complexe.

Calcul de la valeur

En fait, pour ce que tout cela est. Ici, nous sommes censés ajouter une sorte de méthode à Entity

 public Entity Eval() { if (IsLeaf) { return this; } else return MathFunctions.InvokeEval(Name, Children); } 

La feuille est inchangée, mais pour tout le reste, nous avons un calcul personnalisé. Encore une fois, je vais donner un exemple:

 public static Entity Eval(List<Entity> args) { MathFunctions.AssertArgs(args.Count, 1); var r = args[0].Eval(); if (r is NumberEntity) return new NumberEntity(Number.Sin((r as NumberEntity).Value)); else return r.Sin(); } 

Si l'argument est un nombre, alors nous produirons une fonction numérique, sinon nous le renverrons tel qu'il était.

Numéro?

C'est l'unité, le nombre le plus simple. Des opérations arithmétiques peuvent y être effectuées. Par défaut, c'est complexe. Il a également des opérations telles que Sin, Cos et d'autres définies.

Si vous êtes intéressé, le numéro est décrit ici .

Dérivé

Tout le monde peut calculer la dérivée numériquement, et une telle fonction s'écrit vraiment sur une seule ligne:

 public double Derivative(Func<double, double> f, double x) => (f(x + 1.0e-5) - f(x)) * 1.0e+5; 

Mais bien sûr, nous voulons un dérivé analytique. Puisque nous avons déjà un arbre d'expression, nous pouvons remplacer récursivement chaque nœud conformément à la règle de différenciation. Cela devrait fonctionner comme ceci:



Voici, par exemple, comment le montant est implémenté dans mon code:

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) + b.Derive(variable); } 

Mais le travail

 public static Entity Derive(List<Entity> args, VariableEntity variable) { MathFunctions.AssertArgs(args.Count, 2); var a = args[0]; var b = args[1]; return a.Derive(variable) * b + b.Derive(variable) * a; } 

Et voici une solution de contournement en soi:

 public Entity Derive(VariableEntity x) { if (IsLeaf) { if (this is VariableEntity && this.Name == x.Name) return new NumberEntity(1); else return new NumberEntity(0); } else return MathFunctions.InvokeDerive(Name, Children, x); } 

Il s'agit de la méthode Entity. Et comme nous le voyons, la feuille n'a que deux états - soit c'est une variable par laquelle nous différencions, puis sa dérivée est 1, ou c'est une constante (nombre ou VariableEntity), puis sa dérivée est 0, ou un nœud, puis il y a une référence par nom (InvokeDerive fait référence au dictionnaire de fonctions, où se trouve celle désirée (par exemple, la somme ou le sinus)).

Notez que je ne laisse pas quelque chose comme dy / dx ici et dis tout de suite que la dérivée de la variable non par laquelle nous différencions est 0. Mais ici, cela se fait différemment.

Toute différenciation est décrite dans un seul fichier , mais plus n'est pas nécessaire.

Simplification de l'expression. Patterns

La simplification de l'expression n'est généralement pas triviale en principe. Eh bien, par exemple, quelle expression est la plus simple: $$$x ^ 2 - y ^ 2$ ou $$$(x - y) (x + y)$ ? Mais nous adhérons à certaines idées, et sur la base de celles-ci, nous voulons établir ces règles qui simplifient précisément l'expression.

Il est possible d'écrire à chaque Eval que si nous avons la somme et que les enfants sont des œuvres, alors nous trierons quatre options, et si quelque chose est égal quelque part, nous éliminerons le facteur ... Mais bien sûr, je ne veux pas faire ça. Par conséquent, vous pouvez deviner le système de règles et de modèles. Alors que voulons-nous? Quelque chose comme cette syntaxe:

 { any1 / (any2 / any3) -> any1 * any3 / any2 }, { const1 * var1 + const2 * var1 -> (const1 + const2) * var1 }, { any1 + any1 * any2 -> any1 * (Num(1) + any2) }, 

Voici un exemple d'arbre dans lequel un sous-arbre a été trouvé (encerclé en vert) qui correspond au modèle any1 + const1 * any1 (any1 trouvé est encerclé en orange).



Comme vous pouvez le voir, il est parfois important pour nous que la même entité soit répétée, par exemple, pour raccourcir l'expression x + a * x, nous avons besoin de x pour être là et là, car x + a * y n'est plus réduit. Par conséquent, nous devons créer un algorithme qui non seulement vérifie que l’arbre correspond au modèle, mais

1. Vérifiez que le même modèle d'entité correspond à la même entité.
2. Ecrire ce qui correspond à quoi, puis substituer.

Le point d'entrée ressemble à ceci:

 internal Dictionary<int, Entity> EqFits(Entity tree) { var res = new Dictionary<int, Entity>(); if (!tree.PatternMakeMatch(this, res)) return null; else return res; } 

Et dans tree.PaternMakeMatch, nous remplissons récursivement le dictionnaire avec les clés et leurs valeurs. Voici un exemple de liste des entités de modèle elles-mêmes:

 static readonly Pattern any1 = new Pattern(100, PatType.COMMON); static readonly Pattern any2 = new Pattern(101, PatType.COMMON); static readonly Pattern const1 = new Pattern(200, PatType.NUMBER); static readonly Pattern const2 = new Pattern(201, PatType.NUMBER); static readonly Pattern func1 = new Pattern(400, PatType.FUNCTION); 

Lorsque nous écrivons any1 * const1 - func1 et ainsi de suite, chaque nœud aura un numéro - c'est la clé. En d'autres termes, lors du remplissage du dictionnaire, ces nombres apparaîtront sous forme de clés: 100, 101, 200, 201, 400 ... Et lors de la construction d'un arbre, nous regarderons la valeur correspondant à la clé et la remplacerons.

Mis en œuvre ici .

Simplification. Tri des arbres

Dans l' article que j'ai déjà abordé, l'auteur a décidé de le faire simplement, et trié pratiquement par hachage de l'arbre. Il a réussi à réduire a et -a, b + c + b pour tourner 2b + c. Mais nous voulons bien sûr aussi que (x + y) + x * y - 3 * x soit réduit, et en général des choses plus compliquées.

Les modèles ne fonctionnent pas?

En général, ce que nous faisions auparavant, les motifs sont une chose monstrueusement merveilleuse. Cela vous permettra de réduire la différence entre les carrés, et la somme des carrés du sinus et du cosinus, et d'autres choses complexes. Mais la paume élémentaire, ((((((x + 1) + 1) + 1) + 1), elle ne se réduira pas, car la règle principale ici est la commutativité des termes. Par conséquent, la première étape consiste à isoler les «enfants linéaires».

"Enfants linéaires"

En fait, pour chaque nœud de la somme ou de la différence (et, soit dit en passant, le produit / la division), nous voulons obtenir une liste de termes (facteurs).



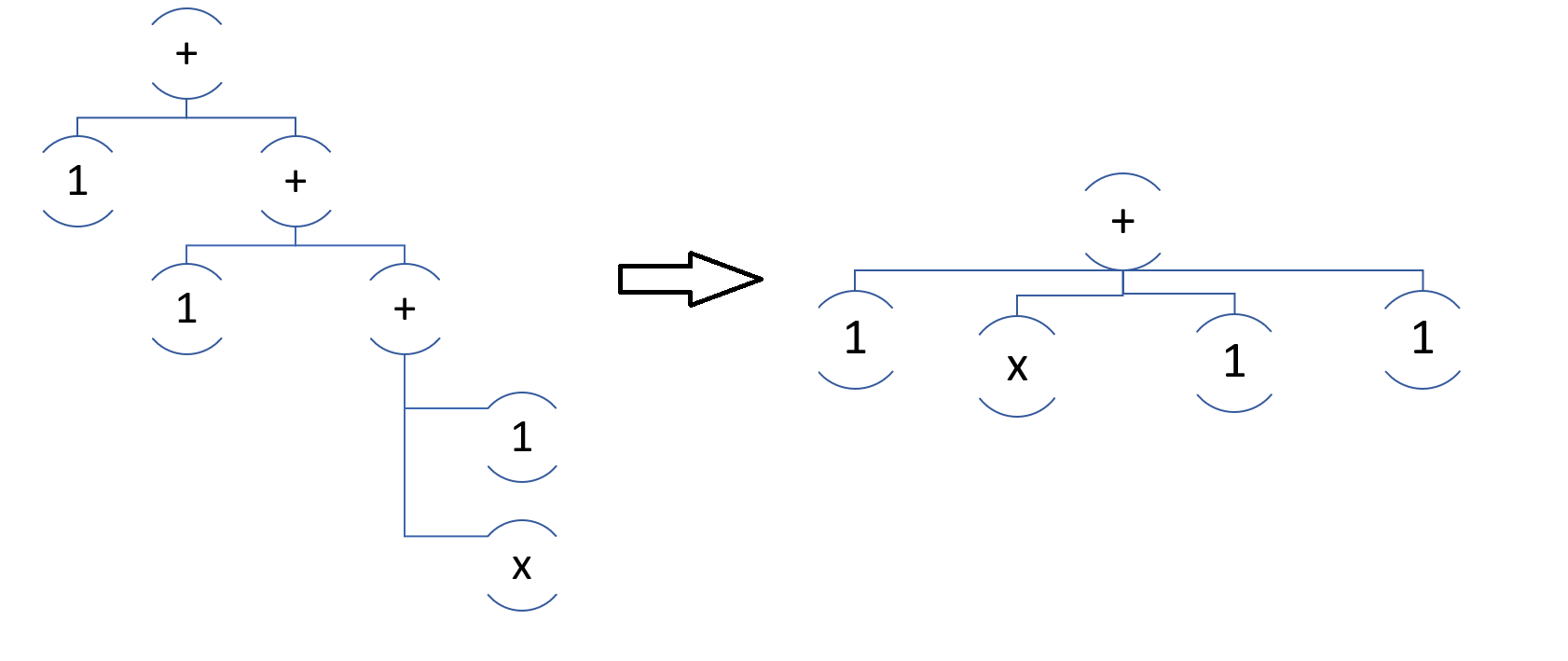
C'est fondamentalement simple. Laissez la fonction LinearChildren (Entity node) renvoyer une liste, puis nous regardons l'enfant dans node.Children: si l'enfant n'est pas une somme, alors result.Add (enfant), sinon result.AddRange (LinearChildren (enfant)).

Pas la plus belle manière mise en œuvre ici .

Regroupement d'enfants

Nous avons donc une liste d'enfants, mais que faire ensuite? Supposons que nous ayons sin (x) + x + y + sin (x) + 2 * x. De toute évidence, notre algorithme recevra cinq termes. Ensuite, nous voulons regrouper par similitude, par exemple, x ressemble à 2 * x de plus que sin (x).

Voici un bon regroupement:



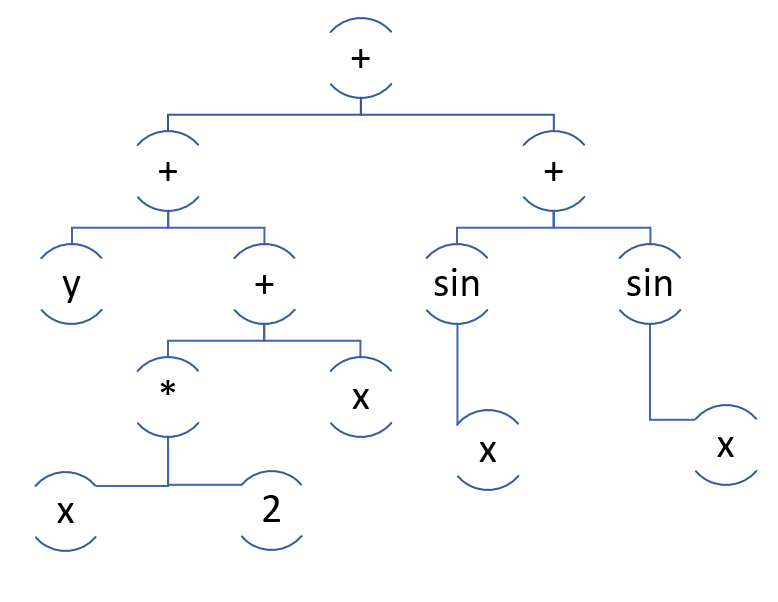
Étant donné que les modèles qu'il contient vont continuer à gérer la conversion de 2 * x + x en 3 * x.

Autrement dit, nous groupons d'abord par un hachage , puis faisons MultiHang - conversion de la sommation n-aire en binaire.

Hachage de nœud

D'une part $$$x$ et $$$x + 1$ devrait être placé dans un groupe. D'un autre côté, si disponible $$$a * x$ mettre en un seul groupe avec $$$y * (x + 1)$ inutile.


Par conséquent, nous implémentons le tri à plusieurs niveaux. Tout d'abord, nous prétendons que $$$x + 1$ - la même chose. Trié, calmé. Ensuite, nous prétendons que $$$x + 1$ ne peut être placé qu'avec d'autres $$$x + 1$ . Et maintenant notre $$$a * (x + 1)$ et $$$y * (x + 1)$ enfin fait équipe. Mis en œuvre tout simplement:

 internal string Hash(SortLevel level) { if (this is FunctionEntity) return this.Name + "_" + string.Join("_", from child in Children select child.Hash(level)); else if (this is NumberEntity) return level == SortLevel.HIGH_LEVEL ? "" : this.Name + " "; else if (this is VariableEntity) return "v_" + Name; else return (level == SortLevel.LOW_LEVEL ? this.Name + "_" : "") + string.Join("_", from child in Children where child.Hash(level) != "" select child.Hash(level)); } 

Comme vous pouvez le voir, la fonction affecte le tri de quelque manière que ce soit (bien sûr, car $$$f (x)$ avec $$$x$ généralement pas connecté dans le cas général). Comme une variable, $$$x$ avec $$$y$ Eh bien, ça ne va pas se mélanger. Mais les constantes et les opérateurs ne sont pas pris en compte à tous les niveaux. Dans cet ordre, le processus de simplification lui-même

 public Entity Simplify(int level) { //      :   ,   ,     . . var stage1 = this.InnerSimplify(); Entity res = stage1; for (int i = 0; i < level; i++) { //     .    -  x  x+1 (  ),  -  x-1  x+1 (,   ),  -  x+1  x+1 ( ). switch (i) { case 0: res = res.Sort(SortLevel.HIGH_LEVEL); break; case 2: res = res.Sort(SortLevel.MIDDLE_LEVEL); break; case 4: res = res.Sort(SortLevel.LOW_LEVEL); break; } //    . res = TreeAnalyzer.Replace(Patterns.CommonRules, res).InnerSimplify(); } return res; } 

Je trie l'arbre ici .

"Compilation" des fonctions

Entre guillemets - car ce n'est pas dans le code IL lui-même, mais seulement dans un ensemble d'instructions très rapide. Mais c'est très simple.

Problème de remplacement

Pour calculer la valeur d'une fonction, il suffit d'appeler la substitution de variable et eval, par exemple

 var x = MathS.Var("x"); var expr = x * x + 3; var result = expr.Substitute(x, 5).Eval(); 

Mais cela fonctionne lentement, environ 1,5 microsecondes par sinus.

Instructions

Pour accélérer le calcul, nous effectuons un calcul de fonction sur la pile, à savoir:

1) Nous arrivons avec la classe FastExpression, qui aura une liste d'instructions

2) Lors de la compilation des instructions sont empilées dans l'ordre inverse, c'est-à-dire, s'il y a une fonction x * x + sin (x) + 3, alors les instructions seront quelque chose comme ceci:

 PUSHVAR 0 //    0 - x CALL 6 //    6 -  PUSHCONST 3 CALL 0 //    0 -  PUSHVAR 0 PUSHVAR 0 CALL 2 CALL 0 

Ensuite, une fois appelé, nous exécutons ces instructions et retournons Number.

Un exemple d'exécution d'une instruction sum:

 internal static void Sumf(Stack<Number> stack) { Number n1 = stack.Pop(); Number n2 = stack.Pop(); stack.Push(n1 + n2); } 

L'appel sinus a été réduit de 1500 à 60 n (le système Complex.Sin fonctionne pendant 30 n).
Le navet est implémenté ici .

Fuh, tout semble être pour le moment. Bien qu'il y ait encore quelque chose à dire, mais il me semble que le volume d'un article est suffisant. Quelqu'un est-il intéressé par la suite? À savoir: analyse à partir d'une chaîne, mise en forme en latex, une certaine intégrale et autres goodies.

Lien vers le référentiel avec tout le code, ainsi que des tests et des échantillons.


Merci de votre attention!